User:Ems57fcva/sandbox/Introduction to special relativity

Einstein

Special relativity is a theory in physics that was developed by Albert Einstein in 1905 to deal with issues raised by classical electrodynamics and the failure of experimental physicists to detect the luminiferous aether (which was postulated to be the medium through which light travels) " (see History of special relativity for a detailed account). In special relativity, how space and time are viewed are dependent on the state of motion of the observer in ways which are incompatible with Newtonian physics.

Special relativity is built on two postulates. The first postulate is called the special principle of relativity, which states that the laws of physics are the same for all observers who are in a state of inertial motion. This is the same principle of relativity that was put forward by Galileo in the 17th century and on which Newtonian physics is based. The second postulate is that the speed of light in a vacuum is a universal constant which is not related to the state of motion of the emitter of the light. Combined, these postulates call for the speed of all beams of light traveling in a vacuum to be the same for all inertial observers no matter how those inertial observers are moving with respect to each other.

Special relativity makes numerous predictions which are incompatible with Newtonian physics. The first such prediction described by Einstein is called the relativity of simultaneity, under which observers who are in motion with respect to each other may disagree on which events occurred at the same time. The relativity of simultaneity is one of the hardest aspects of special relativity to grasp, but it is an essential element of this theory: Without it, many of the other predictions of special relativity cannot be part of a self-consistent theory. The other major predictions of special relativity are time dilation (under which a moving clock ticks more slowly than when it is at rest with respect the observer), length contraction (under which a moving rod may be found to be shorter than when it is at rest with respect to the observer), and the equivalence of mass and energy (written as E=mc²). Special relativity also explains why Maxwell's equations correctly describe the relationship between electricity and magnetism and can do so in any frame of reference.

Special relativity has been tested in many ways, and so far has passed every such test. The most famous of these tests is the Michelson-Morley experiment, the failure of which was one of the things which motivated the creation of special relativity. Other significant tests are the Fizeau experiment (which was first done decades before special relativity was proposed), the detection of the transverse Doppler effect, and the Haefele-Keating experiment. Today, scientists are so comfortable with the idea that the speed of light is always the same that the meter is now defined as being the distance traveled by light in 1/299,792,458^th of a second. This means that the speed of light is now defined as being 299,792,458 m/s.

Background

Newtonian concepts used in special relativity

This section reviews the concepts which special relativity shares with Newtonian physics. It is very important for the reader to have a good grasp of them if they are to understand special relativity. Indeed, the meaning of these concepts is usually taken as a given in articles on relativity theory.

motion refers to how an object is moving with respect to an observer. It is very important to note that all motion is relative. Someone in a car heading down the highway can consider the land, builings, and vegetation beside the highway to be moving from their viewpoint instead of the issue being that the car is moving. In phyisics, both viewpoints are valid. Therefore, motion needs to be stated in terms of what the motion is with respect to. (In the lack of any relative motion, and object can be considered to be "at rest", but even in this case one has to specify what the object is at rest with respect to.)

A frame of reference is a system of observers which are at rest with respect to each other. As such they will share a common view of the universe, and will agree on the relative spatial and temporal relationships between events.

A coordinate system is a way of describing where and when objects are and events occur. For a three-dimensional space, three numbers are required to state where in the space objects are and events occur. In the four-dimensional spacetime of relativity theory, four numbers (three for space and one for time) are needed. Coordinate systems can be constructed in totally arbitrary ways: To be able to describe physical systems, all that is required is that while going between neightboring positions that the coordinate values change in a smooth manner (meaning that there are not sudden jumps in coordinate values), and that each set of coordinate values identifies a single position.

A Cartesian coordinate system is a special kind of coordinate system under which the coordinate lines are linear and always meet at right angles. Under this kind of coordinate system, the laws of physics are at their simplest in both Newtonian physics and special relativity.

The origin of a coordinate system is the place where all of the numbers identifying that position are zero. This usually identifies the coordinate of the current observer, but this is not required to be the case.

Any physical continuum (such as the space of Newtonian physics) can be mapped with an infinite number of coordinate systems. Often, it is necessary to take one's description of the continuum from one coordinate system to another. To do this, a coordinate conversion is specified which relates to coordinates of the destination coordinate system to those of the source coordinate system.

A vector is a set of numbers related to a coordinate system, giving both magnitude and direction. In a three-dimensional space, three numbers are needed to construct a vector. So a coordinate is a vector describing the displacement of the current position from the origin of the coordinate system. Similarly, a velocity is a vector which defines how an object is moving with respect to each coordinate in a coordinate system.

A scalar is a single number. Often, a scalar is the absolute magnitude of a vector. For example, the difference in coordinates between positions is a displacement. The absolute value of a displacement is a distance. Similarly, the abosule cvalue of a velocity is a speed. In a Cartesian coordinate system, the absolute value of vector is given by the square root of the sum of the squares of the component of a vector. (In a two-dimensional space mapped with a Cartesian coordinate system, you end up with an equation for distance that effective states the Pythagorean theorem.)

Simultaneity exists when two events occur at the same time.

Finally, there is the matter of invariants in Newtonian physics: All observers will agree of the times between events and on the distance between events which are simultaneuos. Since the time between events is an invariant, all observers will always agree on which events are simultaneous.

The Galilean transformation

Illustration(s) needed

The Galilean transformation is a simple coordinate conversion that is central to Newtonain physics. Let there be two observers who are in motion with respect to each other and who are mapping their surroundings with a Cartesian coordinate system. The two observers agree on spatial directions that we will call X, Y, and Z and which will be the basis of the coordinate system for each observer. In addition, each observer also has a clock which measures distance in a T direction.

The first observer (whom we will call "John") has a coordinate system for which he is always at the spatial origin. The coordinate components of an event (in space and time) for John are called x, y, x, and t. The other observer (whom we will call "Paul") has a coordinate system for which he is also always at the spatial origin. The coordiantes for Paul will be called x’, y’, z’, and t’. (A coordinate is written as a sequence of the four components in parentheses. So an event that occurs for John at x=2, y=3, z=0, and t=-5 is written as (2, 3, 0, -5).) As seen by John, Paul is moving in the +X direction at a rate of v, and at a time of by the clocks of both John and Paul they will be passing each other. So the event (0,0,0,0) is the same place and time for both John and Paul. As seen by John, Paul is at a position of (vt, 0, 0, t) at any time time t. At that same time t, however, Paul considers himself to be at the position (0, 0, 0, t) in his own cooordinate system. This displacement between the coordinate systems of vt in the X direction is constant for all positions in the spacetime. So there exists a coordinate conversion between John and Paul of

$x'=x-vt$.

$y'=y$,

$z'=z$, and

$t'=t$.

Added basic concepts for special relativity

For special relativity, several added concepts are needed and others are modified.

A closing rate is the rate at which tho objects are approaching each other as perceived by an observer. In Newtonian physics, this would be the same as the relative velocity between the objects as perceived fron the other one. The issue is that in relativity, the composition of velocities is not given by linear vector addition (as is the case for Newtonian physics). However, closing rates always are added linearly.

An event is a four-dimensional vector (or four-vector) identifying a position in both space and time.

Since the speed of light is a constant in special relativity, the determination of the time of an event is given by the equation $t_{e}=t_{o}-d/c$ where $t_{e}$ is the time at which an event occurred in an observer's coordinate system, $t_{o}$ is the time at which the event was perceived by the observer (or when the light emitted at the event reached the observer), d is the distance to the event for the observer, and c is the speed of light.

The distance to an event is as given by rods which are laid out linearly between the observer and the event and which are at rest with respect to the observer.

The iconsistency between Newtonian physics and special relativity

That the special relativity is incompatible with Newtonian physics is easily shown. Let's take the case of observer A shining a light at observer B who is moving straight towards observer A at a rate of v. The light is moving away from observer A at the speed of light (c). In the frame of reference of observer A, the closing rate between the light and observer B is c + v. In Newtonian physics, this closing rate would be the speed of the light for observer B, but in relativity, that is not the case. Instead, in the frame of reference of observer B, the speed of that same light is also c.

To permit observers who are moving with respect to each other to perceive the same speed for light in all cases, the rules of how one's view of space and of time are affected by relative motion cannot be the same as they are in Newtonian physics. Special relativity is the theory the describes those rules for the case of the speed of light being a universal constant.

The basic effects of special relativity

Time dilation

Main article: time dilation

Observer at rest sees time 2L/c

Observer moving parallel relative to setup, sees longer path, time > 2L/c, same speed c

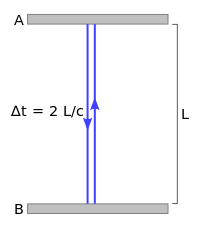
Time dilation is where the passage of time for a moving body is found to be slower than it is for an identical object which is at rest. To see why this is called for by the constancy opf the speed of light, the concept of a light clock is introduced. A light clock is a clock whose "tick" is the back-and-forth passage of a photon of light between two mirrors which are facing each other in a vacuum.

For the case of a light clock which is at rest (as shown in the illustration of the right), the light beam bounces back and forth along the same path. This means that the time of the tick will be 2L/c, where L is the distance between the mirrors and c is the speed of light.

For the case of a moving light clock, the photon has to move with the clock as shown in the illustration on the left. In the case, the distance between the mirrors remains L, but as the photon now has to cover an additional distance during the time it takes to reach the other mirror due to the motion of the mirrors. SInce the speed of light is the same in all frames of reference, this added distance means added time for the photon to move between the mirrors and therefore a slower tick for the moving clock. The effect applies to all clocks in relativity, not just moving clocks.

There is an apparent contradiction here, in that when two observers are in motion with respect to each other, each will consider the other's clock to be slow. This apparent contradiction is resolved by the relativity of simultaneity: Because comoving observers have their view of time "tilted" with respect to the view of the other observer, each obserrver's clock can pass through a coordinate time of the other observer which is greater than the elapsed time on their own clock without contradiction.

Length contraction

Main article: length contraction

Goal: To present a non-mathematical explanation of length contraction. Here the effect of the relativity of simultaneity on the length of a rod is well-known and its used is slmost a given. The light clock, now on its side, can also be used, but a bit of math amy get involved in that case.

The relativity of simultaneity

Main article: relativity of simultaneity

As mentioned in the introduction, the relativity of simultaneity is both the hardest effect of relativity to grasp yet is also the most essential. To describe it in a nutshell, lets first look at the Galiliean position transforation x’ = x - vt. This in essence says that where an event occurs in the frame of reference for a second observer who is in motion with respect to the first observer is a function of when is occurs. In the relatvity of simultaneity, when an event occurs for the second observer is a function of where is occurs.

Illustration(s) needed

A couple of example will help to show how this works. In both cases, we will consider John being on a platform by some train tracks, and Bill being on the train as it is passing by the platform at a velocity in the directins of the tracks of v. In the first example, John is in the center the pltform and Paul is in the center of the train. Let us now suppose that as Bill passes John, he light buld above John burns out with a quick flash. For John, the light from the flash will reach both ends to the plaform at the same time. This is because he is in the center of the plaform, the plaform is not moving woth respect to John, and the speed of the light is the same in all directions for John. For Paul, the flash also occurs in the center of the plaform. However, in Paul's frame of reference the platform is in motion at a velocity of -v. Alao, Paul is also required to find that the speed of the light is the same in all directions and of the same rate as John did. In Paul's view, the closing rae between the light and the end of the platform towards the front of the train is c + v, and the closing rate for the light and the end of the platform towards the back of the train is c - v. This means that the beams of light must get to the ends of the platform at different times as viewed by Paul.

Illustration(s) needed

A second example will help to reinforce this point at also illustrate how the various effects interact. Let the train be of the same length as the platform in John's frame of reference. In this case, at the time when the front to the train is even with the "far" end of the platform (in the view of the train as it approached the platform), the back of the train will be even with the "near" end of the platform. So to John, these events are simultaneuos. Now let us consider the there exists in relativity a length contraction effect for moving objects. This means that in Pauls frame of reference (where the train is not moving since Paul is on it), the train is longer than it was for John. In this same situation, the platform is now moving as so is shorter that is is in John's frame of reference. Both effects conspire to make the train longer than the platform is Paul's frame of reference. That means that the event of the front of the train reaching the far end of the platform must come before the event of the back of the train reaching the near end of the platform. Note that this is the same effect as in the other example.

The "plane of simultaneity" or "surface of simultaneity" contains all those events that happen at the same instant for a given observer. Events that are simultaneous for one observer are not simultaneous for another observer in relative motion.

In both examples, the magnitde of the effect is a function of both the velocity of the other observer and the distance from the first observer in the direction of the second observer's motion to the event in question. So (as stated above) when an event occurs for Paul is a function of both when and where it occurred for John in relativity. Since relativity retains the attribute of Newtonian phyics that where an event occurs is a fucntion of when it occurs, we find the motion in relativity acts to exchange some of space with time and some of time with space. This makes motion act as a rotation in a plane oriented in one direction in space and in the direction of time.

The math of special relativity

The Lorentz transformations

Main article: Lorentz transformations

The coordinate systems

The Lorentz transformations are the mathematical rules under special relativity for going from the (x, y, z, t) coordinate system of one interial oberver (called observer K) into the (x', y', z', t') coordinate system of another inertial observer (called K') who is moving with respect to the first observer. At a set event, the two observers will be passing very close to each observer. This event will be the origin of the coordinate systems.

The issue at this time is what is means by these coordinates. First of all there is the matter of time. It is expected that t = constant will define events that occur at the same time for observer K, and that t' = constant will define events that occur at the same time for observer K'. To deal with the meaning of "at the same time", Einstein created a synchronization procedure: If a beam of light is emitted at time A for an inertial observer, is reflected at an event at time B, and returns to the observer at time C, then since the speed of light is the same for all inertial observers the time of the event is B = (A + C)/2. Another equivalent method assumes that the distance to the event seen at time C is known to be D. In that case, the time of the event is B = C - D/c (where c is the speed of light). In either of these ways, the times t and t' can be assigned to all events. Recall that because of the relativity of simultaneity, observers K and K' do not agree on which events occur at the same time. Also, each observer is measuring time using a standard clock which is at rest with respect to that observer.

For the x and x' coordinates. It is assumed under the Lorentz transformations that the direction of increasing x for observer K is the direction of motion of K' with respect to K. Similarly, the direction of increasing x' is the direction opposite that of the motion of observer K with resoect to observer K'. Additionally, each observer measures distances in the x direction using the length of a stadard rod which is at rest with respect to that observer.

Finally there are the y and z coordinates (for observer K) and the y' and z' coordinates (for observef K'). The requirements here are that these coordinates be perpedicular to the corresponding x or x' axis and also be perpendicular to each other. Additionally, it is expected that the y and y' axes are coincident, and the same for the z and z' axes . Once again, distances are measured along these axes using the standard rod at rest with respect to the observer.

The transformations

Given the coordinate systems as defined in in the previous section, the Lorentz Transformations are

$x'=(x-vt)/{\sqrt {1-v^{2}/c^{2}}}$,

$y'=y$,

$z'=z$, and

$t'=(t-vx/c^{2})/{\sqrt {1-v^{2}/c^{2}}}$.

The effects of special relativity can easily be gleaned from these transformations. In the x transformation, the term x - vt is inhetited from the Galilean transformations. The denominator ${\sqrt {1-v^{2}/c^{2}}}$ encapsulates length contraction: It notes that when the current rod goes in motion that $1/{\sqrt {1-v^{2}/c^{2}}}$ of its lengths is needed for a single unit length in the current at-rest rod to be measured off. In the t transformation, the term t - vx/c^2 encapsulates the relativity of simultaneity. The deminator of ${\sqrt {1-v^{2}/c^{2}}}$ in the time transformation encasulates time dilation in the same way as it encapsulates length contraction for the x transformation.

The t - vx/c^2 term of the t transformation is also the time analog of the x - vt term of the x transformation: It creates a symmetry in the full Lorentz transformations which is a key feature of special relativity. In fact, this featires shows that velocity is a kind of rotation in a plane of space and time.under special relativity.

The Minkowski metric

Main article: Minkowski spacetime

It is a simple mathematical exercise to show that ${x'}^{2}+{y'}^{2}+{z'}^{2}-\left(ct'\right)^{2}=x^{2}+y^{2}+z^{2}-\left(ct\right)^{2}$ for the Lorentz transformations. This fact was pointed out in 1908 by Hermann Minknowski, who used it to show that special relativity is a self-consistent theory which is the physics of a four-dimensional spacetime. This is a subtle but powerful concept which helps to make sense of relativity theory. The underlying idea is that of an "invariant interval" which all observers will agree on as the "distance" between neighboring events. This interval is given by the metric equation

$ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}$.

Four-vectors

Main article: four-vector

Goal: To introduce the concept and describe its immediate consequences.

Momentum and Energy

Let's just say that E=mc² is only one of the things that we can talk about here.

Composition of velocities

Main article: velocity addition formula

Goal: To describe how velocities "add" in relativity

Important tests and applications

Goal: To describe a few of the tests done here. Applications are included since any successful application of SR is effectively a test of it.

Invariance of length: the Euclidean picture

Pythagoras theorem

The modern theory of special relativity begins with the concept of "length". In everyday experience, it seems that the length of objects remains the same no matter how they are rotated or moved from place to place; as a result the simple length of an object doesn't appear to change or is "invariant". However, as is shown in the illustrations below, what is actually being suggested is that length seems to be invariant in a three-dimensional coordinate system.

The length of a line in a two-dimensional coordinate system is given by Pythagoras' theorem:

$h^{2}=x^{2}+y^{2}\,$

One of the basic theorems of vector algebra is that the length of a vector does not change when it is rotated. However, a closer inspection tells us that this is only true if we consider rotations confined to the plane. If we introduce rotation in the third dimension, then we can tilt the line out of the plane. In this case the projection of the line on the plane will get shorter. Does this mean length is not invariant? Obviously not. The world is three-dimensional and in a 3D coordinate system the length is given by the three-dimensional version of Pythagoras's theorem:

$k^{2}=x^{2}+y^{2}+z^{2}\,$

This is invariant under all rotations. The apparent violation of invariance of length only happened because we were 'missing' a dimension. It seems that, provided all the directions in which an object can be tilted or arranged are represented within a coordinate system, the length of an object does not change under rotations. A 3-dimensional coordinate system is enough in classical mechanics because time is assumed absolute and independent of space in that context. It can be considered separately.

Note that invariance of length is not ordinarily considered a dynamic principle, not even a theorem. It is simply a statement about the fundamental nature of space itself. Space as we ordinarily conceive it is called a three-dimensional Euclidean space, because its geometrical structure is described by the principles of Euclidean geometry. The formula for distance between two points is a fundamental property of an Euclidean space, it is called the Euclidean metric tensor (or simply the Euclidean metric). In general, distance formulas are called metric tensors.

Note that rotations are fundamentally related to the concept of length. In fact, one may define length or distance to be that which stays the same (is invariant) under rotations, or define rotations to be that which keep the length invariant. Given any one, it is possible to find the other. If we know the distance formula, we can find out the formula for transforming coordinates in a rotation. If, on the other hand, we have the formula for rotations then we can find out the distance formula.

The Minkowski formulation: introduction of spacetime

After Einstein derived special relativity formally from the counterintuitive proposition that the speed of light is the same to all observers, the need was felt for a more satisfactory formulation. Minkowski, building on mathematical approaches to non-euclidean geometry and the mathematical work of Lorentz and Poincaré, realised that a geometric approach was the key. Minkowski suggested in 1908 that Einstein's new theory could be explained in a natural way if we replaced the concept of separate space and time with one four-dimensional space, spacetime. This was a groundbreaking concept, and Roger Penrose has said that relativity was not truly complete until Minkowski reformulated Einstein's work.

The concept of a four-dimensional space is hard to visualise. It may help at the beginning to think simply in terms of coordinates. In three-dimensional space, one needs three real numbers to refer to a point. In the Minkowski space, one needs four real numbers (three space coordinates and one time coordinate) to refer to a point at a particular instant of time. This point at a particular instant of time, specified by the four coordinates, is called an event. The distance between two different events is called the spacetime interval.

A path through the four-dimensional spacetime, usually called Minkowski space, is called a world line. Since it specifies both position and time, a particle having a known world line has a completely determined trajectory and velocity. This is just like graphing the displacement of a particle moving in a straight line against the time elapsed. The curve contains the complete motional information of the particle.

File:Rel5.GIF

The spacetime interval

In the same way as the measurement of distance in 3D space needed all three coordinates we must include time as well as the three space coordinates when calculating the distance in Minkowski space (henceforth called M). In a sense, the spacetime interval provides a combined estimate of how far two events occur in space as well as the time that elapses between their occurrence.

But there is a problem. Time is related to the space coordinates, but they are not equivalent. Pythagoras's theorem treats all coordinates on an equal footing (see Euclidean space for more details). We can exchange two space coordinates without changing the length, but we can not simply exchange a space coordinate with time, they are fundamentally different. It is an entirely different thing for two events to be separated in space and to be separated in time. Minkowski proposed that the formula for distance needed a change. He found that the correct formula was actually quite simple, differing only by a sign from the Pythagoras's theorem:

$s^{2}=x^{2}+y^{2}+z^{2}-(ct)^{2}\,$

where c is a constant and t is the time coordinate . Multiplication by c, which has the dimension $ms^{-1}$, converts the time to units of length and this constant has the same value as the speed of light. So the spacetime interval between two distinct events is given by

$s^{2}=(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}-c^{2}(t_{2}-t_{1})^{2}\,$

There are two major points to be noted. Firstly, time is being measured in the same units as length by multiplying it by a constant conversion factor. Secondly, and more importantly, the time-coordinate has different sign than the space coordinates. This means that in the four-dimensional spacetime, one coordinate is different from the others and influences the distance differently. This new 'distance' may be zero or even negative. This new distance formula, called the metric of the spacetime, is at the heart of relativity. This simple change of sign leads to completely new hyperbolic geometry that is different from conventional Euclidean geometry. In Minkowski space, Euclid's parallel postulate (also known as the fifth postulate, given in his Elements) does not hold. This distance formula is called the metric tensor of M. This minus sign means that a lot of our intuition about distances can not be directly carried over into spacetime intervals. For example, the spacetime interval between two events separated both in time and space may be zero (see below). From now on, the terms distance formula and metric tensor will be used interchangeably, as will be the terms Minkowski metric and spacetime interval.

In Minkowski spacetime the spacetime interval is the invariant length, the ordinary 3D length is not required to be invariant. The spacetime interval must stay the same under rotations, but ordinary lengths can change. Just like before, we were missing a dimension. Note that everything this far are merely definitions. We define a four-dimensional mathematical construct which has a special formula for distance, where distance means that which stays the same under rotations (alternatively, one may define a rotation to be that which keeps the distance unchanged).

Now comes the physical part. Rotations in Minkowski space have a different interpretation than ordinary rotations. These rotations correspond to transformations of reference frames. Passing from one reference frame to another corresponds to rotating the Minkowski space. An intuitive justification for this is given below, but mathematically this is a dynamical postulate just like assuming that physical laws must stay the same under Galilean transformations (which seems so intuitive that we don't usually recognise it to be a postulate).

Since by definition rotations must keep the distance same, passing to a different reference frame must keep the spacetime interval between two events unchanged. This requirement can be used to derive an explicit mathematical form for the transformation that must be applied to the laws of physics (compare with the application of Galilean transformations to classical laws) when shifting reference frames. These transformations are called the Lorentz transformations. Just like the Galilean transformations are the mathematical statement of the principle of Galilean relativity in classical mechanics, the Lorentz transformations are the mathematical form of Einstein's principle of relativity. Laws of physics must stay the same under Lorentz transformations. Maxwell's equations and Dirac's equation satisfy this property, and hence they are relativistically correct laws (but classically incorrect, since they don't transform correctly under Galilean transformations).

With the statement of the Minkowski metric, the common name for the distance formula given above, the theoretical foundation of special relativity is complete. The entire basis for special relativity can be summed up by the geometric statement "changes of reference frame correspond to rotations in the 4D Minkowski spacetime, which is defined to have the distance formula given above". The unique dynamical predictions of SR stem from this geometrical property of spacetime. Special relativity may be said to be the physics of Minkowski spacetime. The power of this approach was to be realised more fully in general relativity, where the entire phenomena of gravitational interactions are ascribed to the geometry of spacetime.

As has been mentioned before, one can replace distance formulas with rotation formulas. Instead of starting with the invariance of the Minkowski metric as the fundamental property of spacetime, one may state (as was done in classical physics with Galilean relativity) the mathematical form of the Lorentz transformations and require that physical laws be invariant under these transformations. This makes no reference to the geometry of spacetime, but will produce the same result. This was in fact the traditional approach to SR, used originally by Einstein himself. However, this approach is often considered to offer less insight and be more cumbersome than the more natural Minkowski formalism.

Reference frames and Lorentz transformations: relativity revisited

We have already discussed that in classical mechanics coordinate frame changes correspond to Galilean transfomations of the coordinates. Is this adequate in the relativistic Minkowski picture?

Suppose there are two people, Bill and John, on separate planets that are moving away from each other. Bill and John are on separate planets so they both think that they are stationary. John draws a graph of Bill's motion through space and time and this is shown in the illustration below:

File:Rel6.GIF

John's view of Bill and Bill's view of himself

John sees that Bill is moving through space as well as time but Bill thinks he is moving through time alone. Bill would draw the same conclusion about John's motion. In fact, these two views, which would be classically considered a difference in reference frames, are related simply by a coordinate transformation in M. Bill's view of his own world line and John's view of Bill's world line are related to each other simply by a rotation of coordinates. One can be transformed into the other by a rotation of the time axis. Minkowski geometry handles transformations of reference frames in a very natural way.

Changes in reference frame, represented by velocity transformations in classical mechanics, are represented by rotations in Minkowski space. These rotations are called Lorentz transformations. They are different from the Galilean transformations because of the unique form of the Minkowski metric. The Lorentz transformations are the relativistic equivalent of Galilean transformations. Laws of physics, in order to be relativistically correct, must stay the same under Lorentz transformations. The physical statement that they must be same in all inertial reference frames remains unchanged, but the mathematical transformation between different reference frames changes. Newton's laws of motion are invariant under Galilean rather than Lorentz transformations, so they are immediately recognisable as non-relativistic laws and must be discarded in relativistic physics. Schrödinger's equation is also non-relativistic.

Maxwell's equations are trickier. They are written using vectors and at first glance appear to transform correctly under Galilean transformations. But on closer inspection, several questions are apparent that can not be satisfactorily resolved within classical mechanics (see History of special relativity). They are indeed invariant under Lorentz transformations and are relativistic, even though they were formulated before the discovery of special relativity. Classical electrodynamics can be said to be the first relativistic theory in physics. To make the relativistic character of equations apparent, they are written using 4-component vector like quantities called 4-vectors. 4-Vectors transform correctly under Lorentz transformations. Equations written using 4-vectors are automatically relativistic. This is called the manifestly covariant form of equations. 4-Vectors form a very important part of the formalism of special relativity.

Einstein's postulate: the constancy of the speed of light

Einstein's postulate that the speed of light is a constant comes out as a natural consequence of the Minkowski formulation.

Proposition 1:

When an object is travelling at c in a certain reference frame, the spacetime interval is zero.

Proof:

The spacetime interval between the origin-event (0,0,0,0) and an event (x,y,z,t) is

$s^{2}=x^{2}+y^{2}+z^{2}-(ct)^{2}.\,$

The distance travelled by an object moving at velocity v for t seconds is:

${\sqrt {x^{2}+y^{2}+z^{2}}}=vt\,$

giving

$s^{2}=(vt)^{2}-(ct)^{2}.\,$

Since the velocity v equals c we have

$s^{2}=(ct)^{2}-(ct)^{2}.\,$

Hence the spacetime interval between the events of departure and arrival is given by

$s^{2}=0\,$

Proposition 2:

An object travelling at c in one reference frame is travelling at c in all reference frames.

Proof:

Let the object move with velocity v when observed from a different reference frame. A change in reference frame coresponds to a rotation in M. Since the spacetime interval must be conserved under rotation, the spacetime interval must be the same in all reference frames. In proposition 1 we showed it to be zero in one reference frame, hence it must be zero in all other reference frames. We get that

$(vt)^{2}-(ct)^{2}=0\,$

which implies

$|v|=c.\,$

The paths of light rays have a zero spacetime interval, and hence all observers will obtain the same value for the speed of light. Therefore, when assuming that the universe has four dimensions that are related by Minkowski's formula, the speed of light appears as a constant, and does not need to be assumed (postulated) to be constant as in Einstein's original approach to special relativity.

Clock delays and rod contractions: more on Lorentz transformations

Another consequence of the invariance of the spacetime interval is that clocks will appear to go slower on objects that are moving relative to you. This is very similar to how the 2D projection of a line rotated into the third-dimension appears to get shorter. Length is not conserved simply because we are ignoring one of the dimensions. Let us return to the example of John and Bill.

John observes the length of Bill's spacetime interval as:

$s^{2}=(vt)^{2}-(ct)^{2}\,$

whereas Bill doesn't think he has traveled in space, so writes:

$s^{2}=(0)^{2}-(cT)^{2}\,$

The spacetime interval, s², is invariant. It has the same value for all observers, no matter who measures it or how they are moving in a straight line. This means that Bill's spacetime interval equals John's observation of Bill's spacetime interval so:

$(0)^{2}-(cT)^{2}=(vt)^{2}-(ct)^{2}\,$

and

$-(cT)^{2}=(vt)^{2}-(ct)^{2}\,$

hence

$t={\frac {T}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,$.

So, if John sees a clock that is at rest in Bill's frame record one second, John will find that his own clock measures between these same ticks an interval t, called coordinate time, which is greater than one second. It is said that clocks in motion slow down, relative to those on observers at rest. This is known as "relativistic time dilation of a moving clock". The time that is measured in the rest frame of the clock (in Bill's frame) is called the proper time of the clock.

In special relativity, therefore, changes in reference frame affect time also. Time is no longer absolute. There is no universally correct clock, time runs at different rates for different observers.

Similarly it can be shown that John will also observe measuring rods at rest on Bill's planet to be shorter in the direction of motion than his own measuring rods. This is a prediction known as "relativistic length contraction of a moving rod". If the length of a rod at rest on Bill's planet is $X$, then we call this quantity the proper length of the rod. The length $x$ of that same rod as measured on John's planet, is called coordinate length, and given by

$x=X{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\,$.

How Bill's coordinates appear to John at the instant they pass each other

These two equations can be combined to obtain the general form of the Lorentz transformation in one spatial dimension:

${\begin{aligned}T&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\X&=\gamma \left(x-vt\right)\\\end{aligned}}$

or equivalently:

${\begin{aligned}t&=\gamma \left(T+{\frac {vX}{c^{2}}}\right)\\x&=\gamma \left(X+vT\right)\\\end{aligned}}$

where the Lorentz factor is given by $\gamma ={1 \over {\sqrt {1-v^{2}/c^{2}}}}$

The above formulas for clock delays and length contractions are special cases of the general transformation.

Alternatively, these equations for time dilation and length contraction (here obtained from the invariance of the spacetime interval), can be obtained directly from the Lorentz transformation by setting X = 0 for time dilation, meaning that the clock is at rest in Bill's frame, or by setting t = 0 for length contraction, meaning that John must measure the distances to the end points of the moving rod at the same time.

A consequence of the Lorentz transformations is the modified velocity-addition formula:

$s={v+u \over 1+(v/c)(u/c)}$

Simultaneity and clock desynchronisation

The last consequence of Minkowski's spacetime is that clocks will appear to be out of phase with each other along the length of a moving object. This means that if one observer sets up a line of clocks that are all synchronised so they all read the same time, then another observer who is moving along the line at high speed will see the clocks all reading different times. This means that observers who are moving relative to each other see different events as simultaneous. This effect is known as "Relativistic Phase" or the "Relativity of Simultaneity". Relativistic phase is often overlooked by students of special relativity, but if it is understood, then phenomena such as the twin paradox are easier to understand.

The "plane of simultaneity" or "surface of simultaneity" contains all those events that happen at the same instant for a given observer. Events that are simultaneous for one observer are not simultaneous for another observer in relative motion.

Observers have a set of simultaneous events around them that they regard as composing the present instant. The relativity of simultaneity results in observers who are moving relative to each other having different sets of events in their present instant.

The net effect of the four-dimensional universe is that observers who are in motion relative to you seem to have time coordinates that lean over in the direction of motion, and consider things to be simultaneous that are not simultaneous for you. Spatial lengths in the direction of travel are shortened, because they tip upwards and downwards, relative to the time axis in the direction of travel, akin to a rotation out of three-dimensional space.

Great care is needed when interpreting spacetime diagrams. Diagrams present data in two dimensions, and cannot show faithfully how, for instance, a zero length spacetime interval appears.

General relativity: a peek forward

Unlike Newton's laws of motion, relativity is not based upon dynamical postulates. It does not assume anything about motion or forces. Rather, it deals with the fundamental nature of spacetime. It is concerned with describing the geometry of the backdrop on which all dynamical phenomena take place. In a sense therefore, it is a meta-theory, a theory that lays out a structure that all other theories must follow. In truth, Special relativity is only a special case. It assumes that spacetime is flat. That is, it assumes that the structure of Minkowski space and the Minkowski metric tensor is constant throughout. In General relativity, Einstein showed that this is not true. The structure of spacetime is modified by the presence of matter. Specifically, the distance formula given above is no longer generally valid except in space free from mass. However, just like a curved surface can be considered flat in the infinitesimal limit of calculus, a curved spacetime can be considered flat at a small scale. This means that the Minkowski metric written in the differential form is generally valid.

$ds^{2}=dx^{2}+dy^{2}+dz^{2}-c^{2}dt^{2}\,$

One says that the Minkowski metric is valid locally, but it fails to give a measure of distance over extended distances. It is not valid globally. In fact, in general relativity the global metric itself becomes dependent on the mass distribution and varies through space. The central problem of general relativity is to solve the famous Einstein field equations for a given mass distribution and find the distance formula that applies in that particular case. Minkowski's spacetime formulation was the conceptual stepping stone to general relativity. His fundamentally new outlook allowed not only the development of general relativity, but also to some extent quantum field theories.

Mass-energy equivalence: sunlight and atom bombs

Einstein showed that mass is simply another form of energy. The energy equivalent of rest mass m is m*c^2. This equivalence implies that mass should be interconvertible with other forms of energy. This is the basic principle behind atom bombs and production of energy in nuclear reactors and stars (like Sun).

Applications

There is a common perception that relativistic physics is not needed in everyday life. This is not true. Many technologies are critically dependent on relativistic physics:

• Cathode ray tubes ,
• Particle accelerators,
• Global Positioning System (GPS) - although this really requires the full theory of general relativity

The postulates of Special Relativity

Einstein developed Special Relativity on the basis of two postulates:

• First postulate - Special principle of relativity - The laws of physics are the same in all inertial frames of reference. In other words, there are no privileged inertial frames of reference.
• Second postulate - Invariance of c - The speed of light in a vacuum is independent of the motion of the light source.

Special Relativity can be derived from these postulates, as was done by Einstein in 1905. Einstein's postulates are still applicable in the modern theory but the origin of the postulates is more explicit. It was shown above how the existence of a universally constant velocity (the speed of light) is a consequence of modeling the universe as a particular four dimensional space having certain specific properties. The principle of relativity is a result of Minkowski structure being preserved under Lorentz transformations, which are postulated to be the physical transformations of inertial reference frames.

Notes

• The mass of objects and systems of objects has a complex interpretation in special relativity, see relativistic mass.
• "Minkowski also shared Poincaré's view of the Lorentz transformation as a rotation in a four-dimensional space with one imaginary coordinate, and his five four-vector expressions." (Walter 1999).

External links

Special relativity for a general audience (no math knowledge required)

• Einstein Light An award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
• Einstein Online Introduction to relativity theory, from the Max Planck Institute for Gravitational Physics.

Special relativity explained (using simple or more advanced math)

• Wikibooks: Special Relativity
• Albert Einstein. Relativity: The Special and General Theory. New York: Henry Holt 1920. BARTLEBY.COM, 2000
• Usenet Physics FAQ
• Sean Carroll's online Lecture Notes on General Relativity
• Hyperphysics Time Dilation
• Hyperphysics Length Contraction
• Greg Egan's Foundations
• Special Relativity Simulation
• Caltech Relativity Tutorial A basic introduction to concepts of Special and General Relativity, requiring only a knowledge of basic geometry.
• Special Relativity in film clips and animations from the University of New South Wales.
• Relativity Calculator - Learn Special Relativity Mathematics Mathematics of special relativity presented in as simple and comprehensive manner possible within philosophical and historical contexts.

See also

• Special Relativity
• Speed of light
• Invariance
• spacetime especially Distance in spacetime
• Light clock
• Andromeda paradox
• Symmetry
• Symmetry in physics

Category:Special relativity