User:Eifelmuppet/sandbox
Extended Discrete Element Method (XDEM)
[edit]Introduction
[edit]The Extended Discrete Element Method (XDEM) is a recently evolved numerical technique that extends the dynamics of granular material or particles as described through the classical Discrete element method (DEM) (Cundall [1] and Allen [2]) by additional properties such as the thermodynamic state, stress/strain or electro-magnetic field for each particle. Contrary to continuum mechanics concept the Extended Discrete Element Method (XDEM) aims at resolving the particulate phase with its various processes attached to the particles. While the Discrete Element Method predicts position and orientation in space and time for each particles, the Extended Discrete Element Method (XDEM) additionally estimates properties such as internal temperature and/or species distribution or mechanical impact with structures.

History
[edit]Molecular Dynamics developed in the late 1950s by [3] and early 1960s by Rahman [4] may be regarded as a first step pointing in the direction of the Extended Discrete Element Method (XDEM), although the forces due to collisions between particles were replaced by energy potentials e.g.~Lennard-Jones potentials of molecules and atoms as long range forces to determine interaction.
Similarly, the fluid dynamic interaction of particles suspended in a flow were investigated. The drag forces exerted on the particles by the relative velocity by them and the flow were treated as additional forces acting on the particles. Therefore, these multiphase flow phenomena including a solid e.g.~particulate and a gaseous or fluid phase resolve the particulate phase by discrete methods, while gas or liquid flow is described by continuous methods, and therefore, is labelled the Combined Continuum and Discrete Model (CCDM) as applied by [5], Hoomans [6], Xu [7] and Xu [8]. Due to a discrete description of the solid phase, constitutive relations are omitted, and therefore, leads to a better understanding of the fundamentals. This was also concluded by Zhu et al. [9] and Zhu et al.[10] during a review on particulate flows modelled with the CCDM approach. It has seen a mayor development in last two decades and describes motion of the solid phase by the [[Discrete Element Method]] (DEM) on an individual particle scale and the remaining phases are treated by the Navier-Stokes equations. Thus, the method is recognized as an effective tool to investigate into the interaction between a particulate and fluid phase as reviewed by Yu and Xu [11], Feng and Yu [12] and Deen et al. [13]. Based on the CCDM methodology the characteristics of spouted and fluidised beds are predicted by Gryczka et al. [14].
The theoretical foundation for the Extended Discrete Element Method (XDEM) was developed in 1999 by Peters [15], who described incineration of a wooden moving bed on a forward acting grate [16]. The concept was later also employed by Sismsek et al. [17] to predict the furnace process of a grate firing system. Applications to the complex processes of a blast furnace have been attempted by [18]. Numerical simulation of fluid injection into a gaseous environment nowadays is adopted by a large number of CFD-codes codes such as Star-CD of CD-adapco, Ansys and AVL-Fire. Droplets of a spray are treated by a zero-dimensional approach to account for heat and mass transfer to the fluid phase.
Methodology
[edit]Numerous challenges in engineering exist and evolve, that include a continuous and discrete phase simultaneously, and therefore, cannot be solved accurately by continuous or discrete approaches, only. Therefore, the Extended Discrete Element Method (XDEM) provides a platform, that couples discrete and continuous phases for a large number of engineering applications.
Although research and development of numerical methods in each domains of discrete and continuous solvers is still progressing, respective software tools have reached a high degree of maturity. In order to couple discrete and continuous approaches, two major concepts are available:
- Monolithic concept: The equations describing multi-physics phenomena are solved simultaneously by a single solver producing a complete solution.
- Partitioned or staggered concept: The equations describing multi-physics phenomena are solved sequentially by appropriately tailored and distinct solvers with passing the results of one analysis as a load to the next.
The former concept requires a solver that includes a combination of all
physical problems involved, and therefore, requires a large implementation
effort. However, there exist scenarios for which it is difficult to arrange
the coefficients of combined differential equations in one matrix.
A partitioned concept as a coupling between a number of solvers
representing individual domains of physics offers distinctive
advantages over a monolithic concept.

It inherently encompasses a large degree of flexibility by coupling an almost arbitrary number of solvers.
Furthermore, a more modular software development is retained that allows by
far more specific solver techniques adequate to the
problems addressed. However, partitioned simulations impose stable and accurate
coupling algorithms that convince by their pervasive character.
Within the staggered concept of the Extended Discrete Element Method (XDEM)
continuous fields are described by the solution the respective continuous
(conservation) equations. Properties of individual particles such as temperature
are also resolved by solving respective conservation equations that yields both
a spatial and temporal internal distribution of relevant variables.
Mayor conservation principles with their equations and variables
to be solved for and that are employed to an individual particle within the
Extended Discrete Element Method (XDEM) are listed in the
following table.
| Conservation Principle | Equation | Variable |
|---|---|---|
| Mass (compressible medium) | Continuity | Pressure/density |
| Linear Momentum | Navier-Stokes | Velocity |
| Energy | Energy | Temperature |
| Species mass | Species transport | Mass fractions |
| Charge, current | Maxwell | electric, magnetic field, electric displacement field |
The solution of these equations in principle defines a three-dimensional and
transient field of the relevant variables such as temperature or species.
However, the application of these conservation principles to a large number of
particles usually restricts the resolution to at most one representative
dimension and time due to CPU time consumption. Experimental evidence
at least in reaction engineering supports the assumption
of one-dimensionality as pointed out by Man and Byeong [19],
while the importance
of a transient behaviour is stressed by Lee et al. [20], [21]
.
Applications
[edit]
Problems that involve both a continuous and a discrete phase are important in applications as diverse as pharmaceutical industry e.g.~drug production, agriculture food and processing industry, mining, construction and agricultural machinery, metals manufacturing, energy production and systems biology. Some predominant examples are coffee, corn flakes, nuts, coal, sand, renewable fuels e.g.~biomass for energy production and fertilizer.
Initially,
such studies were limited to simple flow configurations as pointed out by Hoomans [22], however, Chu and Yu [23] demonstrated that the method could be applied to a
complex flow configuration consisting of a fluidized bed, conveyor belt and
a cyclone. Similarly, Zhou et al. [24] applied the CCDM
approach to the complex geometry of fuel-rich/lean burner for pulverised
coal combustion in a plant and Chu et al. [25] modelled the complex flow of air, water, coal and magnetite particles of
different sizes in a dense medium cyclone (DMC).
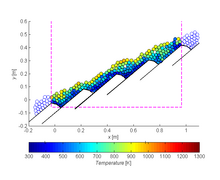
The CCDM approach has also been applied to fluidised beds as reviewed by Rowe and Nienow [26] and Feng and Yu [27] and applied by Feng and Yu [28] to the chaotic motion of particles of different sizes in a gas fluidized bed. Kafuia et al. [29] describe discrete particle-continuum fluid modelling of gas-solid fluidised beds. Further applications of the Extended Discrete Element Method (XDEM) include thermal conversion of biomass on a backward and forward actingn grate. Heat transfer in a packed bed reactor was laso investigated for hot air streaming upward through the packed bed to heat the particles, which dependent on position and size experience different heat transfer rates. The deformation of a conveyor belt due to impacting granular material that is discharged over a chute represents an application in the field of stress/strain analysis.
References
[edit]- ^ Cundall, P. A.; Strack, O. D. L. (1979). "A discrete numerical model for granular assemblies". Geotechnique. 29: 47–65.
- ^ Allen, M. P.; Tildesley, D. J. (1990). Computer Simulation of Liquids. Claredon Press Oxford.
- ^ Alder, B. J.; Wainwright, T. E. (1959). "Studies in Molecular Dynamics. I. General Method". J. Chem. Phys. 31: 459.
- ^ Rahman, A. (1964). "Correlations in the Motion of Atoms in Liquid Argon". Phys. Rev. 136.
- ^ Kawaguchi, T.; Tsuji, Y.; Tanaka, T. (1993). "Discrete particle simulation of two-dimensional fluidized bed". Powder Technol. 77.
- ^ Hoomans, B. P. B.; Kuipers, J. A. M.; Briels, W. J.; Van Swaaij, W. P. M. (1996). "Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach". Chem. Eng. Sci. 51.
- ^ Xu, B. H.; Yu, A. B. (1997). "Numerical simulation of the gas-solid flow in a
fluidized bed by combining discrete particle method with computational fluidd dynamics". Chemical Engineering Science. 52: 2785.
{{cite journal}}: line feed character in|title=at position 48 (help) - ^ Xu, B. H.; Yu, A. B. (1998). "Comments on the paper numerical simulation of
the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics". Chemical Engineering Science. 53: 2646–2647.
{{cite journal}}: line feed character in|title=at position 46 (help) - ^ Zhu, H. P.; Zhou, Z. Y.; Yang, R. Y.; Yu, A. B. (2007). "Discrete particle simulation of particulate systems: Theoretical developments". Chemical Engineering Science. 62: 3378–3396.
- ^ Zhu, H. P.; Zhou, Z. Y.; Yang, R. Y.; Yu, A. B. (2008). "Discrete particle simulation of particulate systems: A review of major applications and findings". Chemical Engineering Science. 63: 5728–5770.
- ^ Xu, B. H.; Yu, A. B. (2003). "Particle-scale modelling of gas-solid flow in fluidisation". Journal of Chemical Technology and Biotechnology. 78: 111–121.
- ^ Feng, Y. Q.; Yu, A. B.; Yu, A. B.; Vince, A. (2004). "Assessment of model formulations in the discrete particle simulation of gas-solid flow". Industrial & Engineering Chemistry Research. 43: 8378–8390.
- ^ Deen, N. G.; Annaland, M. V. S.; Van Der Hoef, M. A.; Kuipers, J. A. M. (2007). "Review of discrete particle modeling of fluidized beds". Chemical Engineering Science. 62: 28–44.
- ^ Gryczka, O.; Heinrich, S.; Deen, N. S.; van Sint Annaland, M.; Kuipers, J. A. M.; Mörl, M. (2009). "CFD modeling of a prismatic spouted bed with two adjustable gas inlets". Canadian Journal of Chemical Engineering. 87: 318–328.
- ^ Peters, B. (1999). "Classification of combustion regimes in a packed bed based on the relevant time and length scales". Combustion and Flame. 116: 297–301.
- ^ Peters, B. (2002). "Measurements and application of a discrete particle model (DPM) to simulate combustion of a packed bed of individual fuel particles". Combustion and Flame. 131: 132–146.
- ^ Simsek, E.; Brosch, B.; Wirtz, S.; Scherer, V.; Kröll, F. (2009). "Numerical simulation of grate firing systems using a coupled CFD/Discrete Element Method (DEM)". Powder Technology. 193: 266–273.
- ^ Natsui, Shungo; Ueda, Shigeru; Fan, Zhengyun; Andersson, Nils; Kano, Junya; Inoue, Ryo; Ariyama, Tatsuro (2010). "Characteristics of solid flow and stress distribution including asymmetric phenomena in blast furnace analyzed by discrete element method". ISIJ International. 50: 207–214.
- ^ Man, Y. H.; Byeong, R. C. (1994). "A numerical study on the combustion of a single carbon particle entrained in a steady flow". Combustion and Flame. 97: 1–16.
- ^ Lee, J. C.; Yetter, R. A.; Dryer, F. L. (1996). "Numerical simulation of laser ignition of an isolated carbon particle in quiescent environment". Combustion and Flame. 105: 591–599.
- ^ Lee, J. C.; Yetter, R. A.; Dryer, F. L. (1996). "Numerical simulation of laser ignition of an isolated carbon particle in quiescent environment". Combustion and Flame. 105: 591–599.
- ^ Hoomans, B. P. B.; Kuipers, J. A. M.; Briels, W. J.; Van Swaaij, W. P. M. (1996). "Discrete particle simulation of bubble and slug formation in a two-dimensional gas-fluidized bed: A hard-sphere approach". Chem. Eng. Sci. 51.
- ^ Chu, K. W.; Yu, A. B. (2008). "Numerical simulation of complex particle-fluid flows". Powder Technology. 179: 104–114.
- ^ Zhou, H.; Mo, G.; Zhao, J.; Cen, K. (2011). "DEM-CFD simulation of the particle dispersion in a gas-solid two-phase flow for a fuel-rich/lean burner". Fuel. 90: 1584–1590.
- ^ Chu, K. W.; Wang, B.; Yu, A. B.; Vince, A.; Barnett, G. D.; Barnett, P. J. (2009). "CFD-DEM study of the effect of particle density distribution on the multiphase flow and performance of dense medium cyclone". Minerals Engineering. 22: 893–909.
- ^ Rowe, P. N.; Nienow, A. W. (1976). "Particle mixing and segregation in gas fluidized beds: A review". Powder Technology. 15: 141–147.
- ^ Feng, Y. Q.; Yu, A. B.; Yu, A. B.; Vince, A. (2004). "Assessment of model formulations in the discrete particle simulation of gas-solid flow". Industrial & Engineering Chemistry Research. 43: 8378–8390.
- ^ Feng, Y. Q.; Yu, A. B. (2008). "An analysis of the chaotic motion of particles of different sizes in a gas fluidized bed". Particuology. 6: 549–556.
- ^ Kafuia, K. D.; Thornton, C.; Adams, M. J. (2002). "Discrete particle-continuum fluid modelling of gas-solid fluidised beds". Chemical Engineering Science. 57: 2395–2410.