User:Duomo Feng/sandbox
Critical embankment velocity is the velocity value of the upper moving vehicle that causes the severe vibration of the embankment and the nearby ground, which is also referred to as the critical speed shortly in the transportation engineering community. This concept and the prediction method was put forward by scholars in civil engineering communities before 1980 [1][2]and stressed and exhaustively studied by Krylov in 1994[3] based on the Green function method and predicted more accurately using other methods in the following. When the vehicles such as high-speed trains or airplanes move approaching or beyond this critical velocity (firstly regarded as the Rayleigh wave speed and later obtained by sophisticated calculation or tests), the vibration magnitudes of vehicles and nearby ground increase rapidly and possibly lead to the damage to the passenagers and the neighboring residents. This relevant unexpected phenomenon is called the ground vibration boom from 1997 when it was observed in Sweden for the first time.[4]
This critical velocity is similar to that of sound which results in the sonic boom. However, there are some differences in terms of the transferring medium. The critical velocity of sound just changes in a small range, although the air quality and the interaction between the jet flight and atmosphere affect the critical velocity. But the embankment including the filling layers and ground soil underneath surface is a typically random medium.[5] Such complex soil-structure coupling vibration system may have several critical velocity values. Therefore the critical embankment velocity belongs to the general concept, the value of which is not constant and should be acquired by calculation or experiment in accordance with certain engineerings nowadays.[6]
Mechanism
[edit]The wave superposition
[edit]Under the ideal assumptions, when the moving loads are imposed on the surface of the embankment, they will induce sub-waves which propagate inside and along the surface of the embankment. If the velocity of the moving loads is less than the propagating waves, which could be the body or surface waves, the vehicles move slowly than the propagating waves and the crests of waves on the embankment surface don't intersect at all.[7] Therefore, there is no superposition of the waves taking place. The vibration of embankment and vehicles changes in a small range under this stage.

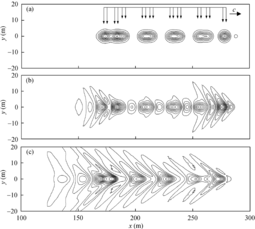
Oppositely, when the operating velocity of the vehicles is greater than the critical velocity, the vehicles move faster gradually and inevitably run at the critical velocity. At that moment, all the crests of the propagating waves coincide in the position where the loads imposed or the wheels and structure contact, which leads to the serious vibration around the vehicles because of the waves superposition. [8](The phenomenon is shown in the schematic figure in the right side)
From this perspective, the critical embankment velocity equals the dominant value of propagating waves velocity.
The structure resonance
[edit]In reality and practical application, the speed of the propagating sub-waves is still related to their frequency components. The total vibration consists of infinite wave components with different frequencies, the magnitude of each sub-wave changes in accordance with the wave speed and different vehicles moving velocity makes different part of sub-waves oscillate maximally.
Obtaining the critical velocity of the embankment is similar with looking for the resonant frequencies of a multi-DOF system.[9] There are many orders of frequencies and the first few ones could make structure vibrate seriously. When the vehicle moves at the critical embankment velocity with respect to the embankment structure, excitation frequency locates very close to the resonant frequencies of most of the propagating waves in the vehicle-embankment coupling structure. [10]Meanwhile, the vehicles moving velocity coincides with most sub-waves.The detailed determination realized by the dispersion analysis to the whole structure and illustrated in the following sections.
The dominant frequencies of the vibration induced by the critical embankment velocity determined according to the specific configuration of the engineering structure. For instance, the loads of moving train passages transfer from wheels through the welded rails, sleepers to the embankment. The discontinuous sleepers under the moving wheels make the cyclic loads imposed on the embankment propagate in low frequencies.[11]
Impact
[edit]Abnormal vibration
[edit]As compared with the relatively low-speed scenarios, the magnitude and range of the vibration of the high-speed line increases. Obviously, the track or pavement structure and the embankment will deteriorate faster as the cyclic loads act repeatedly in the operation period. The performance decrease of the infrastructure gradually makes the even smoothness or the regularities of the rail worse, which demands the operating sectors to add more budgets to the maintenance. More importantly, it is commonly neglected that the vibration of the vehicle itself is magnified under the critical velocity, especially around the area where the wheels interact with the rail.[3] Such high level local vibration can also evidently lead to an increase in the risk of the whole vehicle derailing. That is the real reason why the critical embankment velocity is of much importance.
Low-frequency noise
[edit]Apart from the vibration, the radiation of low-frequency noises induced by vehicle moving at the critical velocity transfer for a very long distance to the residential district. The civilians who live near the line may endure the low-frequency noises for over millions of cycles, which probably makes people feel annoyed, nervous and insomnic as well as even leading to the resonance of human organs. This impacts upon humans are still ignored in the engineering designing process and invoke the research of low frequency noise damage[12].
Prediction
[edit]Calculating the accurate critical embankment velocity of new line is still difficult and should also be verified by many experiments in practical application. However, performing the analytical or numerical modeling even some simple ones gives lots of insights on the qualitative changes of the typical lines, such as exposing the potential issues in the embankment and track structures designing or the ways to relieve the impacts from critical velocity.[13] As the quick development of the HPC, it gradually becomes feasible to predict the feasible critical embankment velocity through numerical methods before the construction of lines.
Elastic foundation beam model
[edit]
Under low frequency ranges (under 100Hz, less than the dominant frequencies of general embankment induced[14]), it's reasonable to obtain the critical embankment velocity through the theory of the beam on elastic foundation.[15] Based on the elastic theory, The dynamic governing equation of the Euler beam on elastic foundation under the moving point load with velocity demonstrates the vertical deflection of the track and sleepers
Herein, , , and represent the material properties related to the track structure and foundation respectively. is the Dirac function determining the location of the point load . The solution of the above equation is derived as[16]
Where is a ratio representing the mechanical difference between the track and foundation. and are the dimensionless parameter associated with the minimal velocity of bend waves of the Euler beam respectively, which are written as[17]
When the velocity of moving vehicles approaches the minimal velocity
Therefore, the minimal phase velocity of bend waves is regarded as the critical embankment velocity in the elastic foundation beam model. Nevertheless, this model is justified for the scenarios when the stiffness of vehicles and track structure is greater than the embankment. The soil-structure interaction and the space dimensional effect are the key factors for the general cases.
Elastic half-space beam model
[edit]If there is no beam putting on the top of the semi-space, the critical velocity of it is Rayleigh wave speed in accordance to the elastic theory, which is smaller than other two types of body wave speed. Furthermore, taking into consideration the above beam and its SSI increasing the number of factors which are related to the critical velocity. The dynamic governing equations of the elastic half-space and beam are respectively[18]

wherein , are the Lamé constants, represents the contacting forces between the semi-space and the beam. The boundary conditions assume the contacting surface is ideally smooth
Based on the decomposition of the elastic potentials and the integral transform, the vertical displacement response of half-space surface can be obtained
Wherein is the wave number in corresponding direction. represents the width of the beam. is the partially transformed value of vertical displacement of half-space surface
Therefore, substitute the expression of vertical displacement into the above, the integral expression related to it in the frequency-wavenumber domain is
The equation above demonstrates the vibration of the beam and half-space respectively. Rewrite it in order to simplify
The first term in the equation above is the dispersion equation of the beam, it has the simple form in this model . The second term represents the relation of the semi-space.
In order to analyze the critical velocity of this coupling structure, the equivalent stiffness of it related to the conventional Winkler foundation in the Fourier domain is needed. In Winkler foundation, the last above equation has this form[18]
Thus, the equivalent stiffness of semi-space of this SSI model to the Winker foundation is , it is written as[19]
The equation above has a really complex form, usually approximate form is used to replace it under practical application. The critical velocity is determined by solving the simultaneous equations with beam model
The critical velocity approximate equation under the Poisson's ratio ranges from 0.2 to 0.38 is[19]
According to this equation, there are two critical velocity values existing in this kind of model. One is less than the Rayleigh wave speed and the other one equals it. Advanced research shows that if the periodic supports are taken into consideration, there is a series of critical velocity values of the elastic half-space.[2]
Multi-layered elastic half-space beam model
[edit]The top part of the embankment consists of many layered structure such as track, ballast or slab and foundation with different material properties. Therefore, a more sophisticated critical velocity analysis on the multi-layered or inhomogeneous structure is needed in the practical application. The critical velocity could be determined in accordance with the dispersion relation of each parts. The radial and vertical surface stresses and displacements of layered half-space in the wavenumber-frequency domain obtained by Thompson–Haskell method is[20]
Herein, represents the stiffness matrix of the whole model. According to Cramer's rule, if the displacements in the frequency domain exist, the determinant of should be equal to zero[10]

Solve it, the surface dispersion curve of the elastic layered foundation has the form below
The first equation explains the change of the horizontal transverse displacement resulted by the SH waves. The second one is related to the P-SV waves. Study shows that the dispersive SH, P-SV waves curves distribute among the ones of the surface Rayleigh wave and shear wave of the half-space, which are non-dispersive waves.[10]
Considering the track structure dispersion relation could obtain more accurate results. For instance the dispersion equation of a typical slab track is written as a function of wavenumber and radial frequency
The intersecting points of dispersion curves of structure components are related to the critical velocity of the embankment. The velocity values could be obtained according to the definition of wavenumber. [21]
Wherein, the represents the excitation frequency of the moving loads. means the different moving directions.
Mitigation
[edit]
For engineering design, improving the critical embankment velocity to a higher value as compared with the operating speed is a conservative way to protect the passengers safety. As the issues related to the critical embankment velocity taking place after the operation of lines for many years, mitigation measures play an imperative role for the refurbished and new lines with high speed moving vehicles.[22] Considering the convenience of the construction, mitigating measures focuses on the areas near the embankment for new lines and upon nearby area for the renovated lines. However, the former ones, active ones, are more efficient as compared with the latter ones, namely the passive measures.
Measures towards the embankment
[edit]The propagating speed of wave inside objects mainly depends on the stiffness index, namely . Therefore the critical embankment velocity could be improved evidently through ground strengthening methods such as pile foundation, grouting, dry deep mixing, etc. The famous Swedish railway line running X2 trains was initially designed using ordinary construction methods. However, since the softness of the top clay, the vibration level induced by the X2 trains was few times higher than that of the conventional trains. The mitigation measure adopted by the operation sector Banverket was dry deep mixing method. After installing a total of 12 trial columns made by special binder with a length of about 8 meters for 2 weeks. The vibration level was reduced to a acceptable value after the mitigation.[23]
Apart from the measures inside the embankment, engineers usually install the damper supports under the rail-pads to isolate the vibration transferred from the wheels downwards. Another common method to weaken the transmission of vibration is to construct the isolating trench with or without filling into porous materials like EPS concrete. [24]
Measures towards the nearby area
[edit]

The vibration transferred to a distant area belongs to the low-frequency ones.[21] For the sensitive architectures like museums, laboratory etc. , damper supports are installed under the building foundations to decrease the extra vibration. Since the magnitude of this kind of vibration cannot be easily reduced, the mitigating measures are mainly adopted to decrease the noise level. The most common way is installing the noise isolation wall near the borders of lines, which could change the direction of the sonic wave because of the reflection effect.[25]
See also
[edit]References
[edit]- ^ Genin, J.; Chung, Y.I. (Nov 1979). "Response of a continuous guideway on equally spaced supports traversed by a moving vehicle". Journal of Sound and Vibration. 67 (2): 245–251. doi:10.1016/0022-460x(79)90487-5. ISSN 0022-460X.
- ^ a b Jezequel, L. (Dec 1980). "Analysis of the critical speeds of a moving load on an infinite periodically supported beam". Journal of Sound and Vibration. 73 (4): 606–609. doi:10.1016/0022-460x(80)90674-4. ISSN 0022-460X.
- ^ a b Krylov, V. V. (May 1994). "On the theory of railway-induced ground vibrations". Le Journal de Physique IV. 04 (C5): C5–769-C5-772. doi:10.1051/jp4:19945167. ISSN 1155-4339.
- ^ Madshus, C (1998). "Ground Dynamics and Man-made Processes: Prediction, Design and Management". Measurement. doi:10.1680/gdamp.26766.
{{cite journal}}: CS1 maint: date and year (link) - ^ Steven Mark, Chrismer (Sep 2015). Railway geotechnics. CRC Press/Taylor & Francis Group. ISBN 9781482288803.
{{cite book}}: CS1 maint: year (link) - ^ Kouroussis, G.; Connolly, D.P.; Verlinden, O. (2014-04-03). "Railway-induced ground vibrations – a review of vehicle effects". International Journal of Rail Transportation. 2 (2): 69–110. doi:10.1080/23248378.2014.897791. ISSN 2324-8378.
- ^ V., Krylov (2019). Ground Vibrations from High-Speed Railways. ICE Publishing. pp. 97–152. ISBN 978-0-7277-6380-8. OCLC 1130022282.
- ^ Mezher, Sara B.; Connolly, David P.; Woodward, Peter K.; Laghrouche, Omar; Pombo, Joao; Costa, Pedro Alves (Mar 2016). "Railway critical velocity – Analytical prediction and analysis". Transportation Geotechnics. 6: 84–96. doi:10.1016/j.trgeo.2015.09.002. ISSN 2214-3912.
- ^ Lei, Xiaoyan (2022). "High Speed Railway Track Dynamics". Advances in High-speed Rail Technology. doi:10.1007/978-981-16-4593-8. ISSN 2363-5010.
- ^ a b c Xia, He; Zhang, Nan; Guo, Weiwei (2018). "Dynamic Interaction of Train-Bridge Systems in High-Speed Railways". Advances in High-speed Rail Technology. doi:10.1007/978-3-662-54871-4. ISSN 2363-5010.
- ^ Connolly, D.P.; Kouroussis, G.; Laghrouche, O.; Ho, C.L.; Forde, M.C. (Sep 2015). "Benchmarking railway vibrations – Track, vehicle, ground and building effects". Construction and Building Materials. 92: 64–81. doi:10.1016/j.conbuildmat.2014.07.042. ISSN 0950-0618.
- ^ Waye, K.P. (2011), "Effects of Low Frequency Noise and Vibrations: Environmental and Occupational Perspectives", Encyclopedia of Environmental Health, Elsevier, pp. 240–253, doi:10.1016/b978-0-444-52272-6.00245-2, ISBN 978-0-444-52272-6, retrieved 2022-06-28
- ^ Connolly, David P.; Marecki, Grzegorz P.; Kouroussis, Georges; Thalassinakis, Ioannis; Woodward, Peter K. (Oct 2016). "The growth of railway ground vibration problems — A review". Science of The Total Environment. 568: 1276–1282. doi:10.1016/j.scitotenv.2015.09.101. ISSN 0048-9697.
- ^ Kouroussis, G; Verlinden, O; Conti, C (2011-10-06). "A two-step time simulation of ground vibrations induced by the railway traffic". Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 226 (2): 454–472. doi:10.1177/0954406211414483. ISSN 0954-4062.
- ^ Grassie, S. L.; Gregory, R. W.; Harrison, D.; Johnson, K. L. (1982). "The Dynamic Response of Railway Track to High Frequency Vertical Excitation". Journal of Mechanical Engineering Science. 24 (2): 77–90. doi:10.1243/jmes_jour_1982_024_016_02. ISSN 0022-2542.
- ^ Krylov, Victor; Ferguson, Colin (1994). "Calculation of low-frequency ground vibrations from railway trains". Applied Acoustics. 42 (3): 199–213. doi:10.1016/0003-682x(94)90109-0. ISSN 0003-682X.
- ^ Doyle, James F. Wave propagation in structures spectral analysis using fast discrete fourier transforms. ISBN 0-387-94940-2. OCLC 636610063.
- ^ a b Huang, Yang H. (2003). Pavement Analysis and Design (2nd ed.). Pearson. ISBN 9780131424739.
- ^ a b Dieterman, H. A.; Metrikine, A. (1996-01-01). "Equivalent stiffness of a half-space interacting with a beam. Critical velocities of a moving load along the beam". European Journal of Mechanics, A/Solids. 15 (1): 67–90. ISSN 0997-7538.
- ^ Sheng, X.; Jones, C.J.C.; Petyt, M. (Aug 1999). "GROUND VIBRATION GENERATED BY A HARMONIC LOAD ACTING ON A RAILWAY TRACK". Journal of Sound and Vibration. 225 (1): 3–28. doi:10.1006/jsvi.1999.2232.
- ^ a b He, Xia; Calçada, Rui (2013). Traffic induced environmental vibrations and controls : theory and application. nova. ISBN 978-1-62618-240-0. OCLC 832284798.
- ^ Ouakka, Slimane; Verlinden, Olivier; Kouroussis, Georges (2022-01-08). "Railway ground vibration and mitigation measures: benchmarking of best practices". Railway Engineering Science. 30 (1): 1–22. doi:10.1007/s40534-021-00264-9. ISSN 2662-4745.
- ^ Takemiya, H. (Jan 2001), "12. Ground vibrations alongside tracks induced by high-speed trains: prediction and mitigation", Noise and vibration from high-speed trains, Thomas Telford Publishing, pp. 347–393
- ^ Lombaert, G.; Degrande, G.; François, S.; Thompson, D. J. (2015), "Ground-Borne Vibration due to Railway Traffic: A Review of Excitation Mechanisms, Prediction Methods and Mitigation Measures", Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Berlin, Heidelberg: Springer Berlin Heidelberg, pp. 253–287, ISBN 978-3-662-44831-1, retrieved 2022-06-30
- ^ Yoon, Jin Young; Pyo, Sukhoon (2019-03-31). "A Review of Mitigation Measures for Reducing Railway Rolling Noise from an Infrastructure Point of View". International Journal of Railway. 12 (1): 1–9. doi:10.7782/ijr.2019.12.1.001. ISSN 1976-9067.











![{\displaystyle w(x,t)={P \over 8EI\beta ^{3}\xi }\exp ^{-\beta \xi |x-v_{0}t|}[\cos({-\beta \psi |x-v_{0}t|})+{\xi \over \psi }\sin({-\beta \psi |x-v_{0}t|})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76cc19d8ed04c06f7332e332386419266b188015)



![{\displaystyle v_{b}={\sqrt[{4}]{4K_{f}EI/m^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c82d443664a9e6e0ddc83180f57614b2ddd9aa2)















![{\displaystyle h(\omega ,k.)\left[1-{\omega D(.) \over 2\pi \mu c_{t}^{2}}\int _{-\infty }^{+\infty }{R_{l} \over \Delta }{\sin(ak.) \over ak.}\operatorname {d} \!k.\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6651a882497fd1928db4784e2f2fa9558187845e)
![{\displaystyle h(\omega ,k.)=[D(.)+\chi (.)]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8223dbd55c37ad168e0834b344dbf74f7dc80fc)



![{\displaystyle h(\omega ,k.)=[D(.)+\chi _{0}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/376237860bc6336bfda9b4288ae43b75f4748b4a)
















