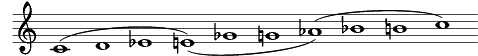User:Dominant7flat9/sandbox

Modes of limited transposition are musical modes or scales that fulfill specific criteria relating to their symmetry and the repetition of their interval groups. The M.O.L.T were compiled by the French composer Olivier Messiaen in his book "The Technique of my Musical Language".

Technical Criteria

Based on our present chromatic system, a tempered system of 12 sounds, these modes are formed of several symmetrical groups, the last note of each group always being common with the first of the following group. At the end of a certain number of chromatic transpositions which varies with each mode, they are no longer transposable, giving exactly the same notes as the first.

There are two ways to view the criteria, however they are interlinked and the criteria of one cannot be fulfilled independently of the other. They are both worth mentioning as they provide different ways to approach and view the criteria of M.O.L.T.

Definition by chromatic transposition

Transposing the major scale up in semitones results in a different set of notes being used each time. Firstly C,D,E,F,G,A,B,C then D♭,E♭,F,G♭,A♭,B♭,C,D♭ etc. This is not the case when transposing the M.O.L.T. For example, the 1st M.O.L.T, the wholetone scale, contains the notes C, D, E, F♯, G♯, A♯, C; transposing this mode up a semitone produces C♯, D♯, F, G, A, B, C♯. Transposing this up another semitone produces D, E, F♯, G♯, A♯, C, D which is exactly the same set of notes we started with. Therefore it can be said that the 1st M.O.L.T only has 2 transpositions.
If any scale has 11 transpositions (one for each note of the chromatic scale) it cannot be a M.O.L.T.

Definition by shifting modal degrees

Breaking down the intervals of the major scale 1,1,½,1,1,1,½ one can see that starting the scale on different degrees will continue to create new modes (with individual interval formations - dorian, phrygian etc.) all the way up to the octave with no repetition. This is not so of the M.O.L.T. The M.O.L.T can only be modally shifted a limited amount of times before repetition of the interval groups occurs. For example take the 1st M.O.L.T or wholetone scale: T,T,T,T,T,T,T One can begin the scale on any degree, it will still have the interval formation: T,T,T,T,T,T,T. Therefore it can be said that the wholetone scale only has 1 mode. The 2nd mode or diminished scale S,T,S,T,S,T,S,T can be arranged 2 ways, either starting with a tone or semitone. Therefore the 2nd M.O.L.T has 2 modes.
If the number of modes for any scale is the same as the number of notes, it cannot be a M.O.L.T.

List of Messiaen's Modes of Limited Transposition

The first mode, also called the whole-tone scale is divided into six groups of two notes each. It has two transpositions and one mode:

The second mode, also called octatonic/diminished/semitone-tone/tone-semitone, is divided into four groups of three notes each. It has three transpositions - like the diminished 7th chord - and two modes:

The third mode is divided into three groups of four notes each. It has four transpositions - like the augmented triad - and three modes:

The fourth mode has six transpositions - like the tri-tone - and four modes:

The fifth mode has six transpositions - like the tri-tone - and three modes:

The sixth mode has six transpositions - like the tri-tone - and four modes:

The seventh mode has six transpositions - like the tri-tone - and five modes:

Expansion and Alteration of the M.O.L.T

Can any more M.O.L.T be found?

The short answer is NO. Their series is closed, it is mathematically impossible to find others of them, at least in our tempered system of 12 semitones. More modes can be found that fit the criteria, but they are simply truncations of the original seven modes.

Truncation

This is the process whereby notes are removed from the original modes leaving new truncated M.O.L.T. The remaining notes must still fulfill the criteria, therefore both the notes removed and those remaining must form repetitive sequences to preserve the symmetry. For example take Mode 1: The whole-tone scale
C D E F♯ G♯ A♯
Removing every other note creates a new truncated M.O.L.T:
Major thirds: C E G♯ C
Removing two notes to every one creates a new truncated M.O.L.T:
Tri-tones: C F♯ C
Removing one note to every two creates a new M.O.L.T:
M3 1 M3 1: C E F♯ A♯ C

In reality the original 7 forms are not 'pure' either, many of the M.O.L.T are truncated forms of one another. Only mode 7 and mode 3 are truly not truncated modes.

Mode 7

Mode 2

Mode 4

Mode 6

Mode 5

Mode 3

Mode 1

List of all M.O.L.T

Original 7 Modes

1) Messiaen's 1st mode (Whole-tone scale/Major seconds), truncation of modes 3,6,7
1 1 1 1 1 1 - C D E F♯ G♯ A♯ C
1 mode
2 transpositions

2) Messiaen's 2nd mode (Diminished Scale/Semitone-tone scale/Tone-semitone scale), truncation of mode 7
½ 1 ½ 1 ½ 1 ½ 1 - C D♭ E♭ E G♭ G A B♭ C
2 modes
3 transpositions

3) Messiaen's 3rd mode
1 ½ ½ 1 ½ ½ 1 ½ ½ - C D E♭ E G♭ G A♭ B♭ B C
3 modes
4 transpositions

4) Messiaen's 4th mode, Truncation of mode 7
½ ½ m3 ½ ½ ½ m3 ½ - C D♭ D F G♭ G A♭ B C
4 modes
6 transpositions

5) Messiaen's 5th mode, Truncation of modes 4,6,7
½ M3 ½ ½ M3 ½ - C D♭ F G♭ G B C
3 modes
6 transpositions

6) Messiaen's 6th mode, truncation of mode 7
1 1 ½ ½ 1 1 ½ ½ - C D E F F♯ G♯ A♯ B C
4 modes
6 transpositions

7) Messiaen's 7th mode
½ ½ ½ 1 ½ ½ ½ ½ 1½ - C D♭ D E♭ F G♭ G A♭ A B C
5 modes
6 transpositions

Pure intervalic truncations

1) Tri-tones, truncation of modes 1,2,3,4,5,6,7
T T - C G♭ C
1 mode
6 transpositions

2) Major thirds, truncation of modes 1,3,6,7
M3 M3 M3 - C E A♭ C
1 mode
4 transpositions

3) Minor thirds, Truncation of modes 2,4,6,7
m3 m3 m3 m3 - C E♭ G♭ A C
1 mode
3 transpositions

1) Whole-tones (mode 1), truncation of modes 3,6,7
1 1 1 1 1 1 - C D E F♯ G♯ A♯ C
1 mode
2 transpositions

Further truncations of the 7 originals

1) Truncation of modes 2,4,6,7
½ 1 m3 ½ 1 m3 - C D♭ E♭ G♭ G A C
3 modes
6 transpositions

2) Truncation of modes 1,2,3,4,5,6,7
M3 1 M3 1 - C E G♭ B♭ C
2 modes
6 transpositions

3) Truncation of modes 2,3,4,5,6,7
P4 ½ P4 ½ - C F G♭ B C
2 modes
6 transpositions

4) Truncation of mode 3
m3 ½ m3 ½ m3 ½ - C E♭ E G A♭ B C
2 modes
4 transpositions

5) Truncation of modes 2,4,6,7
m3 1 ½ m3 1 ½ - C E♭ F G♭ A B C
3 modes
6 transpositions

Use and Sound

Messiaen found ways of employing all of these modes both harmonically, melodically, and sometimes polyphonically.

The wholetone scale has enjoyed quite widespread use since Debussy and other 20th Century composers.

The symmetry inherent in these modes (which means no note can be perceived as the tonic), together with certain rhythmic devices, Messiaen described as containing "the charm of impossibilities."