User:Ct KarenS/sandbox
曳物线 (英文:tractrix)是
is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a tractor (pulling) point that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed.因此它是一条追逐曲线。Claude Perrault在1670年首次引入此概念,后来牛顿 (1676)和惠更斯 (1692)也曾研究过它。
数学推导
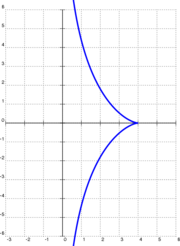
[edit]假设物体被放置在点(a,0) [右图中是(4,0)],而牵引物在原点,那么a就是绳子的长度[图中为4]。然后牵引物开始沿y轴正方向移动。在每个瞬间,绳子都相切于物体画出的曲线,于是该曲线可由以下的微分方程描述:
加上初值条件y(a) = 0,可解出
第一项也可以写成:
其中arsech是反双曲正割函数。
带负号的一支对应于牵引物从原点沿y轴负方向运动的情形。这两支都属于曳物线,它们相交于尖点(a, 0)。
Basis of the tractrix
[edit]The essential property of the tractrix is constancy of the distance between a point P on the curve and the intersection of the tangent line at P with the asymptote of the curve.
The tractrix might be regarded in a multitude of ways:
- It is the locus of the center of a hyperbolic spiral rolling (without skidding) on a straight line.
- The evolute of the catenary function, which describes a fully flexible, inelastic, homogeneous string attached to two points that is subjected to a gravitational field. The catenary has the equation .
- The trajectory determined by the middle of the back axle of a car pulled by a rope at a constant speed and with a constant direction (initially perpendicular to the vehicle).

The function admits a horizontal asymptote. The curve is symmetrical with respect to the y-axis. The curvature radius is
A great implication that the tractrix had was the study of the revolution surface of it around its asymptote: the pseudosphere. Studied by Beltrami in 1868, as a surface of constant negative Gaussian curvature, the pseudosphere is a local model of non-Euclidean geometry. The idea was carried further by Kasner and Newman in their book Mathematics and the Imagination, where they show a toy train dragging a pocket watch to generate the tractrix.
Properties
[edit]
Practical application
[edit]In 1927, P.G.A.H. Voigt patented a horn loudspeaker design based on the assumption that a wave front traveling through the horn is spherical of a constant radius. The idea is to minimize distortion caused by internal reflection of sound within the horn. The resulting shape is the surface of revolution of a tractrix.[1]
Tractrices are also the paths that missiles and torpedoes take as they approach their respective targets.
Drawing machines
[edit]- In October–November 1692, Huygens described three tractrice drawing machines.
- In 1693 Leibniz released to the public a machine which, in theory, could integrate any differential equation; the machine was of tractional design.
- In 1706 John Perks built a tractional machine in order to realise the hyperbolic quadrature.
- In 1729 Johann Poleni built a tractional device that enabled logarithmic functions to be drawn.
See also
[edit]- Dini's surface
- Hyperbolic functions for tanh, sech, csch, arccosh
- Natural logarithm for ln
- Sign function for sgn
- Trigonometric function for sin, cos, tan, arccot, csc
Notes
[edit]References
[edit]- Edward Kasner & James Newman (1940) Mathematics and the Imagination, pp 141–3, Simon & Schuster.
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 5, 199. ISBN 0-486-60288-5.







