User:Colin McTroll/Books/Trigonometry/Notes

In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.

A polygon which has a circumscribed circle is called a cyclic polygon (sometimes a concyclic polygon, because the vertices are concyclic). All regularsimple polygons, all isosceles trapezoids, all triangles and all rectangles are cyclic.

A related notion is the one of a minimum bounding circle, which is the smallest circle that completely contains the polygon within it. Not every polygon has a circumscribed circle, as the vertices of a polygon do not need to all lie on a circle, but every polygon has a unique minimum bounding circle, which may be constructed by a linear time algorithm.[2] Even if a polygon has a circumscribed circle, it may not coincide with its minimum bounding circle; for example, for an obtuse triangle, the minimum bounding circle has the longest side as diameter and does not pass through the opposite vertex.

-is it correct then that: the more obtuse the angle, the greater the difference of A (sz) circumcirc and A (sz) minbound circ
this would seem to pertain - if D is fixed, the A circumcirc inc as < becomes progressively obtuse, so inc A circumcirc over fixed D --> inc
how does the delta < relate to that diff? can we generalize?

??????? sine rule page does not have generalized form in lede, only simplif form, yet overview artic has

Feuerbach point

Excircles

The radii of the excircles are called the exradii. Let the excircle at side AB touch at side AC extended at G, and let this excircle's radius be $r_{c}$ and its center be $I_{c}$. Then $I_{c}G$ is an altitude of $\triangle ACI_{c}$, so $\triangle ACI_{c}$ has area ${\tfrac {1}{2}}br_{c}$. By a similar argument, $\triangle BCI_{c}$ has area ${\tfrac {1}{2}}ar_{c}$ and $\triangle ABI_{c}$ has area ${\tfrac {1}{2}}cr_{c}$. Thus

$\Delta ={\frac {1}{2}}(a+b-c)r_{c}=(s-c)r_{c}$.

So, by symmetry,

$\Delta =sr=(s-a)r_{a}=(s-b)r_{b}=(s-c)r_{c}$.

((this is the same argument as neill 2951 using different symbology --- and seemingly failing to provide a figure))

TP

Another incircle property[edit source]

In a Pythagorean triangle, the radius of the incircle is always an integer. Proof on request. :) Captain Pedant (talk) 18:10, 16 July 2013 (UTC)

This property appears in Pythagorean triple#Elementary properties of primitive Pythagorean triples. It's also true of each excircle. Duoduoduo (talk) 21:26, 16 July 2013 (UTC) Fair enough, no need to duplicate then. :) Captain Pedant (talk) 20:19, 17 July 2013 (UTC)

simple proof rr♭ar♭br♭c=A(sz)^2
simplifies to LHS=RHS ?stated

Why are there gaps in the Euler presentation of Pythag triples

Even functions

ƒ(x) = x² is an example of an even function.

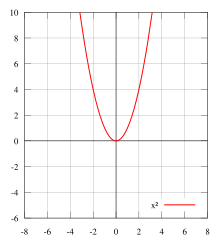
Let f(x) be a real-valued function of a real variable. Then f is even if the following equation holds for all x and -x in the domain of f:

$f(x)=f(-x),\,$

or

$f(x)-f(-x)=0.\,$

Geometrically speaking, the graph face of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis.

Examples of even functions are |x|, x², x⁴, cos(x), cosh(x), or any linear combination of these.

Odd functions

ƒ(x) = x³ is an example of an odd function.

Again, let f(x) be a real-valued function of a real variable. Then f is odd if the following equation holds for all x and -x in the domain of f:

$-f(x)=f(-x),\,$

or

$f(x)+f(-x)=0.\,$

Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin.

Examples of odd functions are x, x³, sin(x), sinh(x), erf(x), or any linear combination of these.

SO if you have a linear combo of even and odd what happens i.e. cos x + sin y notes