User:Cleonis/Time dilation

Special Relativity

The first relativity principle: Galilean relativity

In the history of physics, the stages that can be discerned are stages in recognition of the central position of inertia. In retrospect, the Copernican revolution can be recognized as the first step to making inertia the organizing principle of physics.

Galilei pointed out why it is possible to home in on laws of motion. Imagine you are in a cabin of a boat that is in motion over perfectly smooth water. You are juggling, or you are throwing darts, or something like that. (Galilei used other examples, but that doesn't matter for the content of the reasoning.) Galilei argued: no matter the velocity of the boat, the timing for juggling the balls or the trowing of the darts is the same. This illustrates that there are laws of motion, and to become a skilful juggler is the acquirement of implicit knowledge (motoric knowledge) of how to work with the laws of motion.

The grid of the dartboard serves as a reference, the darter's aim is with respect to that reference system. One layer of 'the same' is that it does not matter where in space the dartboard is positioned, the laws of motion are the same. A second layer is that the velocity of one boat relative to another does not matter either, the laws of motion are the same.

Equivalence class of coordinate systems

Galilei's reasoning introduces an extensive equivalence class. Take the set of all uniform velocities relative to some object that is in inertial motion. For each uniform velocity there is a corresponding coordinate system: the set of all those coordinate systems forms an equivalence class with the property that required skills (juggling skills) are identical for any member of that class. This equivalence class is referred to as 'the equivalence class of inertial coordinate systems'. The large extend of this equivalence class is what makes formulating laws of motion worthwile.

The members of the equivalence class of inertial coordinate systems each have the following property in common: inertia is the same in all directions. That is: if you accelerate an object, then for all directions the same force results in the same acceleration with respect to the inertial coordinate system. This is called the isotropy of inertia. (Isotropy = same in all directions).

Special relativity

Inertia comes about through an interaction of inert mass and the space that the inert mass is located in. A force is required to change the velocity of an object with respect to space. The special theory of relativity deals with the properties of space, with properties of time, and how spacetime continuum is an operative factor in physics. Spacetime has physical properties, and a theory of motion is a theory that describes how spacetime affects the motion of entities with inertial mass.

Synchronisation procedure

Image 1
Three spaceships and a procedure to maintain synchronized fleet time.

The first animation represents a space-time diagram. The yellow lines represent the worldlines of pulses of light that are emitted at t=0. The consecutive frames of the animation combined represent a single diagram.

The three red circles represent a fleet of spaceships. The progressing segments inside the circles represent onboard clocks, counting time. The two orange circles represent miniclocks shuttling back and forth between the ships of the fleet, the miniclocks are used for a procedure to maintain synchronized fleet time. The synchronisation procedure employed here relies on the isotropy of inertia.The ships of the fleet take care that every time the miniclocks are sent on their journey they are in both directions propelled with the equal force.

The ships of the red fleet are 4 units of distance apart. Here, 4 units of distance means that as measured by the clocks of the fleet pulses of light take 4 units of time to propagate from one ship to another. In this article, distance is measured in terms of time: the amount of transit time of pulses of light. In this animation the miniclocks take 5 units of fleet time to travel from one ship to another, so their velocity relative to the fleet is 4/5 the speed of light. During the journey from one ship to another, the miniclocks count 3 units of proper time. This difference in lapse of proper time is called time dilation. The amount of time that elapses for each individual object that is in spacetime is called its proper time.

Relativistic physics does not provide an explanation as to how and why this time dilation occurs. The starting point of relativistic physics is to assume that this is how things are, and the content of the theory consists of working out the ramifications of this assumption. The justification of the assumption is in the success of relativistic theory in applied physics.

Minkowski space-time geometry

Image 2
For an object moving from point O to point A 3 units of proper time elapse.

The line ${\sqrt {t^{2}-x^{2}}}=3$ connects all the points in space-time that have in common that for an object moving with uniform velocity from point O in space-time to any point on that line, 3 units of proper time elapse. In Minkowski space-time, the proper time is a measure of the amount of separation between points in space-time. The amount of separation between point in space-time is called Spacetime interval. The line ${\sqrt {t^{2}-x^{2}}}=3$ is a collection of all the points that are 3 units of proper time away from point O.

The yellow lines that represent pulses of light (which can also be used for a sychronisation procedure) are the most extreme case of time dilation. For light no time elapses in propagating from one point in space to another point. As far as light is concerned, all points in space-time are separated by null-intervals.

An observer situated at the origin can define a coordinate system for himself and any objects that are co-moving with himself, such as the ships of a fleet of spaceships that are co-moving. In the animations of this article the fleet consists of three ships, but it can be any number of ships, and those ships can be regarded as forming a grid. That grid provides a coordinate system to assign a coordinate distance and a coordinate time-lapse between two events. Each ship of the fleet logs the events taking place at its spatial coordinate, noting at what point in fleet time the event took place. The ships of the fleet communicate these logs to each other and on each ship of the fleet a crew member can assemble the information in the logs, and put together a comprehensive spacetime mapping of the events. Animation 1 is an example of such a comprehensive mapping. Note that the comprehensive mapping is not what is directly observed by each individual observer, the comprehensive mapping is an assembled mapping.

The concept of space-time interval in Minkowski space-time is somewhat analogous to the concept of radial distance in Euclidean space. In Euclidean space with 2 dimensions of space there is the relation:

$r^{2}=x^{2}+y^{2}$

The radial distance between two points is an invariant, in the sense that it is independent of the particular choice of mapping a space with a Euclidean coordinate system. Radial distance between two points is invariant under a coordinate transformation that corresponds to a spatial rotation.

The invariant space-time interval of Minkowski space-time geometry is as follows (Here, spatial distance is measured in units of time, the time it takes light to cover the coordinate distance):

(space-time interval)² = (coordinate time)² - (coordinate distance)²

The radical difference is the minus sign. In the case of 3-dimensional Euclidean space, then a sphere around a chosen point of origin constitutes a finite surface with the property that all points on that surface are equally far away from the origin. In the case of Minkowski space-time continuum there is also a "surface" with the property that all points on that surface are an equal space-time interval away from the origin, but in Minkowski space-time this surface is infinitely extended, and it is more a hyperbola than a sphere.

Coordinate translation that involves the dimension of time and under which the space-time interval is invariant corresponds to a change of velocity.

In this article the word 'space' is used in a very abstract sense, in a meaning that is quite different from the everyday meaning of the word. In this article, everything is described in terms of time. Time is counted in units of time, and spatial distance is counted in units of time too! Proper time can be measured, measurement of spatial distance is inherently ambiguous.

Metric of Minkowski space-time

In the context of Euclidean space there is a natural concept of distance between two spatial points: the radial distance. This concept of radial distance is referred to as 'the metric of Euclidean space', as it provides a measure of spatial distance.

In the case of Minkowski space-time it is common to refer to its properties as 'geometry of Minkowski space-time'. (A more accurate expression would be 'chrono-geometry of Minkowski space-time', but that expression is rarely used.) By analogy with the concept of a metric in Euclidean context the formula for the invariant space-time interval is referred to as 'the metric of Minkowski space-time'. The expression 'metric of Minkowski space-time' is common usage, but because of the difference with the general concept of a metric it is also referred to as a 'pseudo-metric'. This signals that while in mathematical expressions the pseudo-metric performs exactly the same function as a metric, it is fundamentally different from a metric.

The concept of a metric can be applied in many different geometric contexts; A simple example of a metric is the metric of the way that in the game of chess the King moves around. To go from one corner to another along a column or a row takes 7 steps, and to go diagonally also takes 7 steps. That metric is an example of a non-euclidean metric, for Pythagoras' theorem does not apply.

The metric of Minkowski space-time, with the square of one dimension being subtracted from the square of another dimension, is unexplained. There is no theory to address the question of how the structure of space and time can be like that. At present, the Minkowski space-time geometry must be assumed in order to be able to formulate a theory at all.

Equivalence of different coordinate mappings

Image 3
A fleet of ships maintaining synchronized fleet time.

The three dark green circles represent a fleet of spaceships. As in the first animations miniclocks are shuttling back and forth between the ships of the fleet, as part of a procedure to maintain synchronized fleet time.

This space-time diagram represents how the motion of the green fleet in space-time is mapped in a coordinate system that has a velocity of 2/5 the speed of light with respect to the green fleet.

The metric of Minkowsk spacetime informs us how everything will proceed for the green fleet. The central ship sends the miniclocks in opposite directions and each miniclock has a relative velocity of 4/5 of the speed of light with respect to the fleet. For each leg of the procedure, the miniclocks count 3 units of proper time, and the fleet clocks count 5 units of proper time for each leg of the procedure.

Image 4
Two equally valid representations of synchronisation procedures.

This image shows space-time diagrams that map both the procedure of the red fleet and the procedure of the green fleet. The diagram on the left shows a mapping of events in space-time in a coordinate system that is co-moving with the green fleet, the diagram on the right shows a mapping of events in space-time in a coordinate system that is co-moving with the red fleet.

In this particular case the synchronisation procedure and its mapping in a spacetime diagram was introduced with the red fleet first, mapping the physics in a coordinate system that is co-moving with the red fleet. It could also have been introduced with the green fleet first, mapping the physics in a coordinate system that is co-moving with the green fleet. According to special relativity there is complete symmetry between the two coordinate representations. As mapped in the red-fleet-coordinate system, the shuttling miniclocks of the green fleet do not reach the outer ships simultaneously. However, as mapped in the green-fleet-coordinate system they do. This is called relativity of simultaneity.

Relativity of simultaneity

It is worthwile to explore what is meant here with relativity of simultaneity. It would be possible to challenge the relativity of simultaneity as introduced here if there would be some hidden layer to the physics taking place. It is tempting to suppose that maybe, underneath the appearances, objects do have a particular velocity with respect to some fixed background reference. Suppose it is the red fleet that is actually stationary with respect to the background reference and that the green fleet has a velocity of 2/5th of the speed of light with respect to the background reference, and suppose that there would be a way to ascertain this velocity with respect to the background reference. Then there would be an absolute criterium for simultaneity. The point of special relativity is to leave no room for some hidden layer beneath the appearances; special relativity asserts unconditional symmetry, and the two mappings that are presented in image 4 are an example of that. The full symmetry implies relativity of simultaneity.

The Principle of relativity of inertial motion

The concept of Minkowski spacetime continuum is deeply interlinked with the principle of relativity of inertial motion. Minkowski spacetime continuum is seen as an embodiment of the principle of relativity of inertial motion. In fact, it can be regarded as embodying the principle of relativity of inertial motion more profoundly than the classical concept of space and time.

The synchronisation procedure that the fleets use relies on the isotropy of inertia. Both the red fleet and the green fleet make sure that in expelling the miniclocks the same amount of kinetic energy is transferred to each of them. Then the speed of the miniclocks relative to the ships of the fleet must be the same for all miniclocks. That the speed of the miniclocks is consistent is confirmed by the fact that the transit time, both in terms of proper time as measured by the miniclocks, and in terms of fleet time, is always the same.

When Galilei formulated the principle of relativity of inertial motion, the obvious supposition was that velocity-vectors add in the same way as vectors of euclidean space add. The assumption of galilean relativity is an assumption (a most intuitive one) about the chrono-geometric structure of space and time. At first sight it appears that galilean relativity is the only possible embodiment of the principle of relativity of inertial motion. The revolution of special relativity was in the recognition that there is yet another chrono-geometric structure that embodies the principle of relativity of inertial motion: Minkowski spacetime. (Palash B. Pal has written up some very neat derivations, showing how both galilean relativity and special relativity satisfy the principle of relativity of inertial motion. Nothing but relativity (PDF-file 64 KB))

An interesting extremum is when very light objects (subatomic particles such as protons, neutrons and electrons) are expelled, and the velocity of the particles is very close to the speed of light. Then both as observed from the red fleet and observed from the green fleet, the expelled particles are seen to propagate away from the emitter at (very close to) the speed of light (independent of direction). Light itself is at the very extremal point. Given the physical properties of Minkowski spacetime, light always propagates away from any emitter with a relative velocity of c, regardless of the velocity of that emitter relative to other emitters.

Fundamental unification: a single principle of inertia

In Minkowski spacetime, the members of the equivalence class of inertial coordinate systems have the following properties in common:
- Inertia of particles is isotropic
- Propagation of light is isotropic
The achievement of the special theory of relativity is placing motion of matter and propagation of light in a unified framework; both particles and light are subject to a single principle of inertia. The key is Minkowski spacetime, the concept of Minkowski spacetime allows unification of the description of motion of particles and propagation of electromagnetic waves.

Thus, centuries after the Copernican revolution, special relativity goes a step further in recognizing inertia as an organizing principle of physics.

Spacetime as a physical entity

Spacetime is assumed to be a physical entity, participating in the physics taking place. The nature of this participation is that the amount of proper time that elapses in travelling from a certain point A to a certain point B is path dependent. In travelling from point A to point B along a trajectory that is not the spatially shortest trajectory, a smaller amount of proper time elapses than when travelling along the spatially shortest path. The major difference between ether theories and relativistic physics (arguably the only difference), is that in the case of relativistic physics velocity with respect to the assumed background structure (spacetime), does not enter the theory.

Equivalence class of coordinate systems

Image 5
A class of equivalent coordinate systems.

In this animation, a series of Minkowski coordinate systems is shown. The sequence of frames of the animation is a sequence of coordinate systems with a relative velocity. As there is a velocity-step between each pair of frames, the motion of the spaceships and clocks is mapped differently in each frame. All individual frames of the animation represent the physics taking place equally well. Together, the set of all frames in which the physics taking place is represented equally well constitutes an equivalence class of coordinate systems.

A number of physical properties are the same in all representations. An example of a physical property that is the same in all spacetime mappings is the spacetime interval. Because proper time is invariant under the coordinate transformations, proper time is regarded as true time.

The animation also suggests what happens during physical acceleration. During physical acceleration, an object's relation to its surroundings changes.

Symmetric velocity time dilation

Image 6

The situation is symmetrical. The red fleet and the green fleet have a velocity relative to each other, so for each unit of red time less than one unit of green time elapses, and for each unit of green time, less than one unit of red time elapses.

At time t=0 the two central ships of both fleets pass each other. At t=0, let the red ship emit a signal with a particular frequency, as measured in red fleet time. The green ship receives that signal, and that signal will be shifted to a lower frequency, as measured by green fleet time.

Conversely: at t=0 let the green ship emit a signal with a particular frequency, as measured in green fleet time. The red ship receives that signal, and that signal will be shifted to a lower frequency, as measured by red fleet time.

This type of time dilation is called symmetric velocity time dilation. An example of that is the trajectories of the time-disseminating shuttles in the animations. At all times the shuttles have a velocity relative to each other, so there is a corresponding symmetric velocity time dilation. When the shuttles rejoin it is seen that there no difference in the amount of elapsed proper time.

Asymmetric velocity time dilation

Image 7
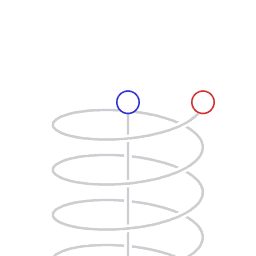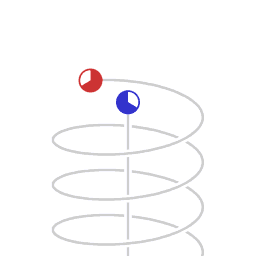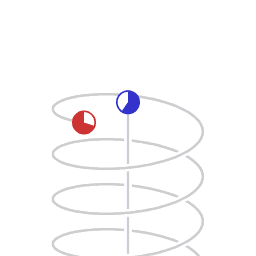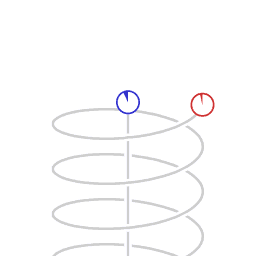
Asymmetric velocity time dilation

Schematic representation of asymmetric velocity time dilation. The animation represents motion as mapped in a Minkowski space-time diagram, with two dimensions of space, (the horizontal plane) and position in time vertically. The circles represent clocks, counting lapse of proper time. The Minkowski coordinate system is co-moving with the non-accelerating clock.

The clock in circular motion counts less lapse of proper time than the non-accelerating clock. Here, the difference in the amount of lapse of proper time is in a ratio of 1:2, which corresponds to a transversal velocity of 0.866 times the speed of light.

Any light emitted by the non-accelerating clock and received by the circling clock is received as a blue-shifted signal, in a ratio of 1:2. Any light emitted by the circling clock and received by the non-accelerating clock is received as a red-shifted signal, in a ratio of 2:1 .

In this situation, symmetry is broken, and there is a difference in amount of proper time that elapses.