User:ByteHamster/sandbox-merge

This is the user sandbox of ByteHamster. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here.

Other sandboxes: Main sandbox | Template sandbox

Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!

Merge-Algorithmen (von [merge] Error: {{Langx}}: text has italic markup (help) ‚verschmelzen‘) ist eine Familie von Algorithmen, die mehrere sortierte Listen als Eingabe erhalten und eine sortierte Liste ausgeben, welche alle Elemente der Eingabelisten enthält. Merge-Algorithmen werden in vielen Algorithmen als Unterprogramm verwendet. Ein bekannter Algorithmus dafür ist Mergesort

Anwendung

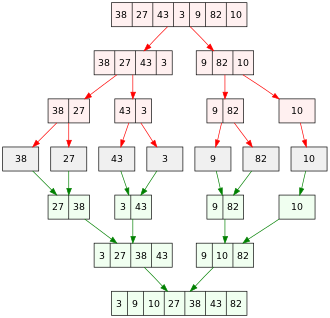
Der Merge-Algorithmus spielt eine wichtige Rolle im Mergesort Algorithmus, einem vergleichsbasierten Sortieralgorithmus. Konzeptionell besteht der Mergesort-Algorithmus aus zwei Schritten:

Teile die Eingabe rekursiv in kürzere Listen von ungefähr gleicher Länge, bis jede Liste nur noch ein Element enthält. Eine Liste, welche nur ein Element enthält, ist nach Definition sortiert.
Verschmelze wiederholt die kürzeren Listen, bis eine einzelne Liste alle Elemente enhthält. Diese Liste ist nun die fertig sortierte Liste.

Der Merge-Algorithmus wird im Mergesort-Algorithmus immer wieder ausgeführt.

Ein Beispiel für Mergesort wird im Bild dargestellt. Man beginnt mit einer unsortierten Liste aus 7 Zahlen. Das Array wird in 7 Partitionen aufgeteilt, wovon jede nur ein Element enthält. Die sortierten Listen werden verschmolzen, um längere sortierte Listen zu liefern, bis nur noch eine sortierte Liste übrig ist.

Merging two lists

Das Verschmelzen von zwei sortierten Listen kann in linearer Zeit und linearem Platz erfolgen. Der folgende Pseudocode zeigt einen Algorithmus, welcher zwei Listen $A$ und $B$ in eine neue Liste $C$ verschmilzt.^[1]. Die Funktion kopf ergibt das erste Element der Liste. Entfernen des ersten Elements wird typischerweise über das Inkrementieren eines Pointers realisiert.

program merge(A, B)
    eingabe A, B : Liste
    ausgabe Liste

    C := neue leere Liste
    solange A ist nicht leer und B ist nicht leer
        wenn kopf(A) ≤ kopf(B) dann
            hänge kopf(A) an C an
            entferne den Kopf von A
        sonst
            hänge kopf(B) an C an
            entferne den Kopf von B

    // Nun ist entweder A oder B leer. Nun muss noch die andere Liste an C angehängt werden.
    solange A ist noch nicht leer
        hänge kopf(A) an C an
        entferne den Kopf von A
    solange B ist noch nicht leer
        hänge kopf(B) an C an
        entferne den Kopf von B

    ausgabe C

Das Erstellen einer neuen Liste $C$ kann vermieden werden, dadurch wird der Algorithmus allerdings langsamer und schwerer zu verstehen. ^[2]

k-Wege-Mischen

The k-way merge problem consists of merging k sorted arrays to produce a single sorted array with the same elements. Denote by n the total number of elements. n is equal to the size of the output array and the sum of the sizes of the k input arrays. For simplicity, we assume that none of the input arrays is empty. As a consequence k < n, which simplifies the reported running times. The problem can be solved in O(n log k) running time with O(n) space. Several algorithms that achieve this running time exist.

Direktes k-Wege-Mischen

The basic idea of a direct k-way merge consists of efficiently computing the minimum element of all k arrays and then transferring it to the output array.

A straightforward implementation would scan all k arrays to determine the minimum. This straightforward implementation results in a running time of Θ(kn). Note that this is mentioned only as a possibility, for the sake of discussion. Although it would work, it is not efficient.

We can improve upon this by computing the smallest element faster. By using either heaps, tournament trees, or splay trees, the smallest element can be determined in O(log k) time. The resulting running times are therefore in O(n log k).

Heap

Turnierbaum

TODO User:ByteHamster/sandbox-k-way-merge

References

^ Skiena, Steven (2010). The Algorithm Design Manual (2nd ed.). Springer Science+Business Media. p. 123. ISBN 1-849-96720-2.
^ Katajainen, Jyrki; Pasanen, Tomi; Teuhola, Jukka (1996). "Practical in-place mergesort". Nordic J. Computing. 3 (1): 27–40. CiteSeerX 10.1.1.22.8523.

Siehe auch

Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Pages 158–160 of section 5.2.4: Sorting by Merging. Section 5.3.2: Minimum-Comparison Merging, pp. 197–207.
Mergesort

Kategorie:Sortieralgorithmus

[skiena-1] Skiena, Steven (2010). The Algorithm Design Manual (2nd ed.). Springer Science+Business Media. p. 123. ISBN 1-849-96720-2.

[2] Katajainen, Jyrki; Pasanen, Tomi; Teuhola, Jukka (1996). "Practical in-place mergesort". Nordic J. Computing. 3 (1): 27–40. CiteSeerX 10.1.1.22.8523.

[1]

[2]