User:Brown.ry/sandbox

Wikipedia policies

Text

Wikipedia:Identifying_reliable_sources_(medicine)

Fourier_transform

Riemann_zeta_function

Permutation

http://www.google.com

This text should be referenced.

This text should also be referenced.

Enumeration of magic squares

As mentioned above, the set of normal squares of order three constitutes a single equivalence class-all equivalent to the Lo Shu square. Thus there is basically just one normal magic square of order 3. But the number of distinct normal magic squares rapidly increases for higher orders. There are 880 distinct magic squares of order 4 and 275,305,224 of order 5. The number of distinct normal squares is not yet known for any higher order.

Semi-log plot of Pn, the probability of magic squares of dimension n

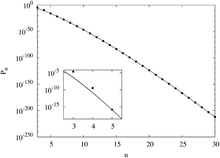
Algorithms tend to only generate magic squares of a certain type or classification, making counting all possible magic squares quite difficult. Traditional counting methods have proven unsuccessful, statistical analysis using the Monte Carlo method has been applied. The basic principle applied to magic squares is to randomly generate n × n matrices of elements 1 to n² and check if the result is a magic square. The probability that a randomly generated matrix of numbers is a magic square is directly proportional to the number of magic squares.

More intricate versions of the Monte Carlo method, such as the exchange Monte Carlo, and Monte Carlo Backtracking have produced even more accurate estimations. Using these methods it has been shown that the probability of magic squares decreases rapidly as n increases. Using fitting functions give the curves seen to the right.