User:Blindman shady/Trig

In mathematics, trigonometric identities are equalities that involve trigonometric functions that are true for every single value of the occurring variables. These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common trick involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity.

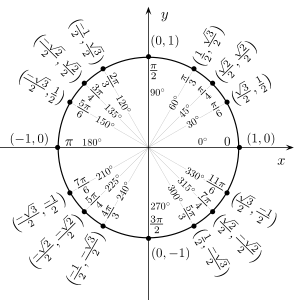
All of the trigonometric functions of an angle θ can be constructed geometrically in terms of a unit circle centered at O.

Cosines & Sines around the unit circle

Notation

To avoid the confusion caused by the ambiguity of sin⁻¹(x), the reciprocals and inverses of trigonometric functions are often displayed as in this table. In representing the cosecant function, the longer form 'cosec' is sometimes used in place of 'csc'.

Function		Inverse function		Reciprocal		Inverse reciprocal
sine	sin	arcsine	arcsin	cosecant	csc	arccosecant	arccsc
cosine	cos	arccosine	arccos	secant	sec	arcsecant	arcsec
tangent	tan	arctangent	arctan	cotangent	cot	arccotangent	arccot

Different angular measures can be appropriate in different situations. This table shows some of the more common systems. Radians is the default angular measure and is the one you use if you use the exponential definitions. All angular measures are unitless.

Degrees	30	45	60	90	120	180	270	360
Radians	$\pi /6$	$\pi /4$	$\pi /3$	$\pi /2$	$2\pi /3$	$\pi$	$3\pi /2$	$2\pi$
Grads	33 ⅓	50	66 ⅔	100	133 ⅓	200	300	400

Basic relationships

Pythagorean trigonometric identity	$\sin ^{2}\theta +\cos ^{2}\theta =1\,$
Ratio identity	$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$

From the two identities above, the following table can be extrapolated. Note however that these conversion equations may not provide the correct sign (+ or −). For example, if sin θ = 1/2, the conversion in the table indicates that $\scriptstyle \cos \theta \,=\,{\sqrt {1-\sin ^{2}\theta }}={\sqrt {3}}/2$, though it is possible that $\scriptstyle \cos \theta \,=\,-{\sqrt {3}}/2$. More information would be needed about which quadrant θ lies in to determine a single, exact answer.

Each trigonometric function in terms of the other five.

Function	sin	cos	tan	csc	sec	cot
$\sin \theta =$	$\sin \theta \$	${\sqrt {1-\cos ^{2}\theta }}$	${\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}$	${\frac {1}{\csc \theta }}$	${\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}$	${\frac {1}{\sqrt {1+\cot ^{2}\theta }}}$
$\cos \theta =$	${\sqrt {1-\sin ^{2}\theta }}$	$\cos \theta \$	${\frac {1}{\sqrt {1+\tan ^{2}\theta }}}$	${\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}$	${\frac {1}{\sec \theta }}$	${\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}$
$\tan \theta =$	${\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}$	${\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}$	$\tan \theta \$	${\frac {1}{\sqrt {\csc ^{2}\theta -1}}}$	${\sqrt {\sec ^{2}\theta -1}}$	${\frac {1}{\cot \theta }}$
$\csc \theta =$	${1 \over \sin \theta }$	${1 \over {\sqrt {1-\cos ^{2}\theta }}}$	${{\sqrt {1+\tan ^{2}\theta }} \over \tan \theta }$	$\csc \theta \$	${\sec \theta \over {\sqrt {\sec ^{2}\theta -1}}}$	${\sqrt {1+\cot ^{2}\theta }}$
$\sec \theta =$	${1 \over {\sqrt {1-\sin ^{2}\theta }}}$	${1 \over \cos \theta }$	${\sqrt {1+\tan ^{2}\theta }}$	${\csc \theta \over {\sqrt {\csc ^{2}\theta -1}}}$	$\sec \theta \$	${{\sqrt {1+\cot ^{2}\theta }} \over \cot \theta }$
$\cot \theta =$	${{\sqrt {1-\sin ^{2}\theta }} \over \sin \theta }$	${\cos \theta \over {\sqrt {1-\cos ^{2}\theta }}}$	${1 \over \tan \theta }$	${\sqrt {\csc ^{2}\theta -1}}$	${1 \over {\sqrt {\sec ^{2}\theta -1}}}$	$\cot \theta \$

Historic shorthands

Rarely used today, the versine, coversine, haversine, and exsecant have been defined as below and used in navigation, for example the haversine formula was used to calculate the distance between two points on a sphere.

Name(s)	Abbreviation(s)	Value
versed sine versine	${\textrm {versin}}\,\theta$ ${\textrm {vers}}\,\theta$	$1-\cos \theta \,$
coversed sine coversine	${\textrm {coversin}}\,\theta$ ${\textrm {cover}}\,\theta$	$1-\sin \theta \,$
haversed sine haversine	${\textrm {haversin}}\,\theta$ ${\textrm {hav}}\,\theta$	${\tfrac {1}{2}}{\textrm {versin}}\theta \,$
hacoversed sine hacoversine cohaversine havercosine	${\textrm {hacoversin}}\,\theta$ ${\textrm {hacov}}\,\theta$	${\tfrac {1}{2}}{\textrm {coversin}}\theta \,$
exsecant	${\textrm {exsec}}\,\theta \,$	$\sec \theta -1\,$
excosecant	${\textrm {excsc}}\,\theta \,$	$\csc \theta -1\,$

Symmetry, shifts, and periodicity

By examining the unit circle, the following properties of the trigonometric functions can be established.

Symmetry

When the trigonometric functions are reflected from certain values of $\theta$, The result is often one of the other trigonometric functions. This leads to the following identities:

Reflected in $\theta =0$	Reflected in $\theta =\pi /2$ (co-function identities)	Reflected in $\theta =\pi$
${\begin{aligned}\sin(0-\theta )&=-\sin \theta \\\cos(0-\theta )&=+\cos \theta \\\tan(0-\theta )&=-\tan \theta \\\csc(0-\theta )&=-\csc \theta \\\sec(0-\theta )&=+\sec \theta \\\cot(0-\theta )&=-\cot \theta \end{aligned}}$	${\begin{aligned}\sin({\tfrac {\pi }{2}}-\theta )&=+\cos \theta \\\cos({\tfrac {\pi }{2}}-\theta )&=+\sin \theta \\\tan({\tfrac {\pi }{2}}-\theta )&=+\cot \theta \\\csc({\tfrac {\pi }{2}}-\theta )&=+\sec \theta \\\sec({\tfrac {\pi }{2}}-\theta )&=+\csc \theta \\\cot({\tfrac {\pi }{2}}-\theta )&=+\tan \theta \end{aligned}}$	${\begin{aligned}\sin(\pi -\theta )&=+\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \\\csc(\pi -\theta )&=+\csc \theta \\\sec(\pi -\theta )&=-\sec \theta \\\cot(\pi -\theta )&=-\cot \theta \\\end{aligned}}$

Shifts and periodicity

By shifting the function round by certain angles, it is often possible to find different trigonometric functions that express the result more simply. Some examples of this are shown by shifting functions round by π/2, π and 2π radians. Because the periods of these functions are either π or 2π, there are cases where the new function is exactly the same as the old function without the shift.

Shift by π/2	Shift by π Period for tan and cot	Shift by 2π Period for sin, cos, csc and sec
${\begin{aligned}\sin(\theta +{\tfrac {\pi }{2}})&=+\cos \theta \\\cos(\theta +{\tfrac {\pi }{2}})&=-\sin \theta \\\tan(\theta +{\tfrac {\pi }{2}})&=-\cot \theta \\\csc(\theta +{\tfrac {\pi }{2}})&=+\sec \theta \\\sec(\theta +{\tfrac {\pi }{2}})&=-\csc \theta \\\cot(\theta +{\tfrac {\pi }{2}})&=-\tan \theta \end{aligned}}$	${\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=+\tan \theta \\\csc(\theta +\pi )&=-\csc \theta \\\sec(\theta +\pi )&=-\sec \theta \\\cot(\theta +\pi )&=+\cot \theta \\\end{aligned}}$	${\begin{aligned}\sin(\theta +2\pi )&=+\sin \theta \\\cos(\theta +2\pi )&=+\cos \theta \\\tan(\theta +2\pi )&=+\tan \theta \\\csc(\theta +2\pi )&=+\csc \theta \\\sec(\theta +2\pi )&=+\sec \theta \\\cot(\theta +2\pi )&=+\cot \theta \end{aligned}}$

Angle sum and difference identities

These are also known as the addition and subtraction theorems or formulæ. The quickest way to prove these is Euler's formula.

Sine	$\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \,$	Note: From plus-minus sign. $x\pm y=a\pm b\Rightarrow \ x+y=a+b\ {\mbox{or}}\ x-y=a-b$ $x\pm y=a\mp b\Rightarrow \ x+y=a-b\ {\mbox{or}}\ x-y=a+b$
Cosine	$\cos(\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \,$
Tangent	$\tan(\alpha \pm \beta )={\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}$

Matrix form

Main article: matrix multiplication

The sum and difference formulas for sine and cosine can be written in matrix form, thus:

$\left[{\begin{matrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{matrix}}\right]\left[{\begin{matrix}\cos \beta &-\sin \beta \\\sin \beta &\cos \beta \end{matrix}}\right]=\left[{\begin{matrix}\cos(\alpha +\beta )&-\sin(\alpha +\beta )\\\sin(\alpha +\beta )&\cos(\alpha +\beta )\end{matrix}}\right].$

Sines and cosines of sums of infinitely many terms

$\sin \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {odd} \ k\geq 1}(-1)^{(k-1)/2}\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)$

$\cos \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{\mathrm {even} \ k\geq 0}~(-1)^{k/2}~~\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)$

In these two identities an asymmetry appears that is not seen in the case of sums of finitely many terms: in each product, there are only finitely many sine factors and cofinitely many cosine factors. If only finitely many of the terms θ_i are nonzero, then only finitely many of the terms on the right side will be nonzero because sine factors will vanish, and in each term, all but finitely many of the cosine factors will be unity.

Tangents of sums of finitely many terms

Let x_i = tan(θ_i ), for i = 1, ..., n. Let e_k be the kth-degree elementary symmetric polynomial in the variables x_i, i = 1, ..., n, k = 0, ..., n. Then

$\tan(\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},$

the number of terms depending on n. For example:

${\begin{aligned}\tan(\theta _{1}+\theta _{2}+\theta _{3})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&{}={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&{}={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}$

and so on. The general case can be proved by mathematical induction.

Multiple-angle formulae

Tn is the nth Chebyshev polynomial	$\cos n\theta =T_{n}(\cos \theta )\,$
Sn is the nth spread polynomial	$\sin ^{2}n\theta =S_{n}(\sin ^{2}\theta )\,$
de Moivre's formula, $i$ is the Imaginary unit	$\cos n\theta +i\sin n\theta =(\cos(\theta )+i\sin(\theta ))^{n}\,$

$1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}.$

(This function of x is the Dirichlet kernel.)

Double-, triple-, and half-angle formulae

These can be shown by using either the sum and difference identities or the multiple-angle formulae.

Double-angle formulae
${\begin{aligned}\sin 2\theta &=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}$	${\begin{aligned}\cos 2\theta &=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}$	$\tan 2\theta ={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\,$	$\cot 2\theta ={\frac {\cot ^{2}\theta -1}{2\cot \theta }}\,$
Triple-angle formulae
$\sin 3\theta =3\sin \theta -4\sin ^{3}\theta \,$	$\cos 3\theta =4\cos ^{3}\theta -3\cos \theta \,$	$\tan 3\theta ={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}$	$\cot 3\theta ={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}$
Half-angle formulae
$\sin {\tfrac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}$	$\cos {\tfrac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}}$	${\begin{aligned}\tan {\tfrac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\end{aligned}}$	${\begin{aligned}\cot {\tfrac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {1+\cos \theta \over 1-\cos \theta }}\\&={\frac {\sin \theta }{1-\cos \theta }}\\&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}$

See also Tangent half-angle formula.

Sine, cosine, and tangent of multiple angles

$\sin n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\sin \left({\frac {1}{2}}(n-k)\pi \right)$

$\cos n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\cos \left({\frac {1}{2}}(n-k)\pi \right)$

tan nθ can be written in terms of tan θ using the recurrence relation:

$\tan \,(n{+}1)\theta ={\frac {\tan n\theta +\tan \theta }{1-\tan n\theta \,\tan \theta }}.$

cot nθ can be written in terms of cot θ using the recurrence relation:

$\cot \,(n{+}1)\theta ={\frac {\cot n\theta \,\cot \theta -1}{\cot n\theta +\cot \theta }}.$

Tangent of an average

$\tan \left({\frac {\alpha +\beta }{2}}\right)={\frac {\sin \alpha +\sin \beta }{\cos \alpha +\cos \beta }}=-\,{\frac {\cos \alpha -\cos \beta }{\sin \alpha -\sin \beta }}$

Setting either α or β to 0 gives the usual tangent half-angle formulas.

Euler's infinite product

$\cos \left({\theta \over 2}\right)\cdot \cos \left({\theta \over 4}\right)\cdot \cos \left({\theta \over 8}\right)\cdots =\prod _{n=1}^{\infty }\cos \left({\theta \over 2^{n}}\right)={\sin(\theta ) \over \theta }.$

Power-reduction formulae

Obtained by solving the second and third versions of the cosine double-angle formula.

Sine	Cosine	Other
$\sin ^{2}\theta ={\frac {1-\cos 2\theta }{2}}$	$\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}$	$\sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos 4\theta }{8}}$
$\sin ^{3}\theta ={\frac {3\sin \theta -\sin 3\theta }{4}}$	$\cos ^{3}\theta ={\frac {3\cos \theta +\cos 3\theta }{4}}$	$\sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin 2\theta -\sin 6\theta }{32}}$
$\sin ^{4}\theta ={\frac {3-4\cos 2\theta +\cos 4\theta }{8}}$	$\cos ^{4}\theta ={\frac {3+4\cos 2\theta +\cos 4\theta }{8}}$	$\sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos 4\theta +\cos 8\theta }{128}}$
$\sin ^{5}\theta ={\frac {10\sin \theta -5\sin 3\theta +\sin 5\theta }{16}}$	$\cos ^{5}\theta ={\frac {10\cos \theta +5\cos 3\theta +\cos 5\theta }{16}}$	$\sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin 2\theta -5\sin 6\theta +\sin 10\theta }{512}}$

and in general terms of powers of sin θ or cos θ the following is true, and can be deduced using De Moivre's formula, Euler's formula and binomial expansion.

	Cosine	Sine
${\mbox{if }}n{\mbox{ is odd}}$	$\cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {(n-2k)\theta }$	$\sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{({\frac {n-1}{2}}-k)}{\binom {n}{k}}\sin {(n-2k)\theta }$
${\mbox{if }}n{\mbox{ is even}}$	$\cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {(n-2k)\theta }$	$\sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{({\frac {n}{2}}-k)}{\binom {n}{k}}\cos {(n-2k)\theta }$

Product-to-sum and sum-to-product identities

The product-to-sum identities can be proven by expanding their right-hand sides using the angle addition theorems. See beat frequency for an application of the sum-to-product formulas.

Product-to-sum $\cos \theta \cos \varphi ={\cos(\theta -\varphi )+\cos(\theta +\varphi ) \over 2}$ $\sin \theta \sin \varphi ={\cos(\theta -\varphi )-\cos(\theta +\varphi ) \over 2}$ $\sin \theta \cos \varphi ={\sin(\theta +\varphi )+\sin(\theta -\varphi ) \over 2}$ $\cos \theta \sin \varphi ={\sin(\theta +\varphi )-\sin(\theta -\varphi ) \over 2}$

Sum-to-product $\sin \theta +\sin \varphi =2\sin \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)$ $\cos \theta +\cos \varphi =2\cos \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)$ $\cos \theta -\cos \varphi =-2\sin \left({\theta +\varphi \over 2}\right)\sin \left({\theta -\varphi \over 2}\right)$ $\sin \theta -\sin \varphi =2\cos \left({\theta +\varphi \over 2}\right)\sin \left({\theta -\varphi \over 2}\right)\;$

Other related identities

If x, y, and z are the three angles of any triangle, or in other words

${\mbox{if }}x+y+z=\pi ={\mbox{half circle,}}\,$

${\mbox{then }}\tan(x)+\tan(y)+\tan(z)=\tan(x)\tan(y)\tan(z).\,$

(If any of x, y, z is a right angle, one should take both sides to be ∞. This is neither +∞ nor −∞; for present purposes it makes sense to add just one point at infinity to the real line, that is approached by tan(θ) as tan(θ) either increases through positive values or decreases through negative values. This is a one-point compactification of the real line.)

${\mbox{If }}x+y+z=\pi ={\mbox{half circle,}}\,$

${\mbox{then }}\sin(2x)+\sin(2y)+\sin(2z)=4\sin(x)\sin(y)\sin(z).\,$

Ptolemy's theorem

${\mbox{If }}w+x+y+z=\pi ={\mbox{half circle,}}\,$

${\begin{aligned}{\mbox{then }}&\sin(w+x)\sin(x+y)\\&{}=\sin(x+y)\sin(y+z)\\&{}=\sin(y+z)\sin(z+w)\\&{}=\sin(z+w)\sin(w+x)=\sin(w)\sin(y)+\sin(x)\sin(z).\end{aligned}}$

(The first three equalities are trivial; the fourth is the substance of this identity.) Essentially this is Ptolemy's theorem adapted to the language of trigonometry.

Linear combinations

For some purposes it is important to know that any linear combination of sine waves of the same period but different phase shifts is also a sine wave with the same period, but a different phase shift. In the case of a linear combination of a sine and cosine wave (which is just a sine wave with a phase shift of π/2), we have

$a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )\,$

where

$\varphi =\arcsin \left({\frac {b}{\sqrt {a^{2}+b^{2}}}}\right)+{\begin{cases}0&{\text{if }}a\geq 0,\\\pi &{\text{if }}a<0,\end{cases}}$

or equivalently

$\varphi =\arctan \left({\frac {b}{a}}\right)+{\begin{cases}0&{\text{if }}a\geq 0,\\\pi &{\text{if }}a<0.\end{cases}}$

More generally, for an arbitrary phase shift, we have

$a\sin x+b\sin(x+\alpha )=c\sin(x+\beta )\,$

where

$c={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }},\,$

and

$\beta =\arctan \left({\frac {b\sin \alpha }{a+b\cos \alpha }}\right).$

Other sums of trigonometric functions

Sum of sines and cosines with arguments in arithmetic progression:

$\sin {\varphi }+\sin {(\varphi +\alpha )}+\sin {(\varphi +2\alpha )}+\cdots +\sin {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \sin {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.$

$\cos {\varphi }+\cos {(\varphi +\alpha )}+\cos {(\varphi +2\alpha )}+\cdots +\cos {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \cos {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.$

For any a and b:

$a\cos(x)+b\sin(x)={\sqrt {a^{2}+b^{2}}}\cos(x-\arctan(b,a))\;$

where arctan(y, x) is the generalization of arctan(y/x) which covers the entire circular range (see also the account of this same identity in "symmetry, periodicity, and shifts" above for this generalization of arctan).

$\tan(x)+\sec(x)=\tan \left({x \over 2}+{\pi \over 4}\right).$

The above identity is sometimes convenient to know when thinking about the Gudermannian function, which relates the circular and hyperbolic trigonometric functions without resorting to complex numbers. If x, y, and z are the three angles of any triangle, i.e. if x + y + z = π, then

$\cot(x)\cot(y)+\cot(y)\cot(z)+\cot(z)\cot(x)=1.\,$

Certain linear fractional transformations

If ƒ(x) is given by the linear fractional transformation

$f(x)={\frac {(\cos \alpha )x-\sin \alpha }{(\sin \alpha )x+\cos \alpha }},$

and similarly

$g(x)={\frac {(\cos \beta )x-\sin \beta }{(\sin \beta )x+\cos \beta }},$

then

$f(g(x))=g(f(x))={\frac {(\cos(\alpha +\beta ))x-\sin(\alpha +\beta )}{(\sin(\alpha +\beta ))x+\cos(\alpha +\beta )}}.$

More tersely stated, if for all α we let ƒ_α be what we called ƒ above, then

$f_{\alpha }\circ f_{\beta }=f_{\alpha +\beta }.\,$

If x is the slope of a line, then ƒ(x) is the slope of its rotation through an angle of −α.

Inverse trigonometric functions

$\arcsin(x)+\arccos(x)=\pi /2\;$

$\arctan(x)+\operatorname {arccot}(x)=\pi /2.\;$

$\arctan(x)+\arctan(1/x)=\left\{{\begin{matrix}\pi /2,&{\mbox{if }}x>0\\-\pi /2,&{\mbox{if }}x<0\end{matrix}}\right.$

Compositions of trig and inverse trig functions

$\sin[\arccos(x)]={\sqrt {1-x^{2}}}\,$	$\tan[\arcsin(x)]={\frac {x}{\sqrt {1-x^{2}}}}$
$\sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}$	$\tan[\arccos(x)]={\frac {\sqrt {1-x^{2}}}{x}}$
$\cos[\arctan(x)]={\frac {1}{\sqrt {1+x^{2}}}}$	$\cot[\arcsin(x)]={\frac {\sqrt {1-x^{2}}}{x}}$
$\cos[\arcsin(x)]={\sqrt {1-x^{2}}}\,$	$\cot[\arccos(x)]={\frac {x}{\sqrt {1-x^{2}}}}$

Relation to the complex exponential function

$e^{ix}=\cos(x)+i\sin(x)\,$ (Euler's formula),

$e^{-ix}=\cos(-x)+i\sin(-x)=\cos(x)-i\sin(x)\,$

$e^{i\pi }=-1\,$

$\cos(x)={\frac {e^{ix}+e^{-ix}}{2}}\;$

$\sin(x)={\frac {e^{ix}-e^{-ix}}{2i}}\;$

and hence the corollary:

$\tan(x)={\frac {e^{ix}-e^{-ix}}{i({e^{ix}+e^{-ix}})}}\;={\frac {\sin(x)}{\cos(x)}}$

where $i^{2}=-1$.

Infinite product formula

For applications to special functions, the following infinite product formulæ for trigonometric functions are useful:

$\sin x=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)$

$\sinh x=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right)$

${\frac {\sin x}{x}}=\prod _{n=1}^{\infty }\cos \left({\frac {x}{2^{n}}}\right)$

$\cos x=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)$

$\cosh x=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}(n-{\frac {1}{2}})^{2}}}\right)$

Identities without variables

The curious identity

$\cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}}$

is a special case of an identity that contains one variable:

$\prod _{j=0}^{k-1}\cos(2^{j}x)={\frac {\sin(2^{k}x)}{2^{k}\sin(x)}}.$

A similar-looking identity is

$\cos {\frac {\pi }{7}}\cos {\frac {2\pi }{7}}\cos {\frac {3\pi }{7}}={\frac {1}{8}},$

and in addition

$\sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}}.$

The following is perhaps not as readily generalized to an identity containing variables (but see explanation below):

$\cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.$

Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators:

$\cos \left({\frac {2\pi }{21}}\right)\,+\,\cos \left(2\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(4\cdot {\frac {2\pi }{21}}\right)$

$\,+\,\cos \left(5\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(8\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.$

The factors 1, 2, 4, 5, 8, 10 may start to make the pattern clear: they are those integers less than 21/2 that are relatively prime to (or have no prime factors in common with) 21. The last several examples are corollaries of a basic fact about the irreducible cyclotomic polynomials: the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the Möbius function evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.

Computing π

An efficient way to compute π is based on the following identity without variables, due to Machin:

${\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}$

or, alternatively, by using Euler's formula:

${\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}.$

A useful mnemonic for certain values of sines and cosines

For certain simple angles, the sines and cosines take the form $\scriptstyle {\sqrt {n}}/2$ for 0 ≤ n ≤ 4, which makes them easy to remember.

${\begin{matrix}\sin 0&=&\sin 0^{\circ }&=&{\sqrt {0}}/2&=&\cos 90^{\circ }&=&\cos \left({\frac {\pi }{2}}\right)&={\sqrt {0}}/2\\\\\sin \left({\frac {\pi }{6}}\right)&=&\sin 30^{\circ }&=&{\sqrt {1}}/2&=&\cos 60^{\circ }&=&\cos \left({\frac {\pi }{3}}\right)&={\sqrt {1}}/2\\\\\sin \left({\frac {\pi }{4}}\right)&=&\sin 45^{\circ }&=&{\sqrt {2}}/2&=&\cos 45^{\circ }&=&\cos \left({\frac {\pi }{4}}\right)&={\sqrt {2}}/2\\\\\sin \left({\frac {\pi }{3}}\right)&=&\sin 60^{\circ }&=&{\sqrt {3}}/2&=&\cos 30^{\circ }&=&\cos \left({\frac {\pi }{6}}\right)&={\sqrt {3}}/2\\\\\sin \left({\frac {\pi }{2}}\right)&=&\sin 90^{\circ }&=&{\sqrt {4}}/2&=&\cos 0^{\circ }&=&\cos 0&={\sqrt {4}}/2\end{matrix}}$

Other interesting values

$\sin {\frac {\pi }{7}}={\frac {\sqrt {7}}{6}}-{\frac {\sqrt {7}}{189}}\sum _{j=0}^{\infty }{\frac {(3j+1)!}{189^{j}j!\,(2j+2)!}}\!$

$\sin {\frac {\pi }{18}}={\frac {1}{6}}\sum _{j=0}^{\infty }{\frac {(3j)!}{27^{j}j!\,(2j+1)!}}\!$

With the golden ratio φ:

$\cos \left({\frac {\pi }{5}}\right)=\cos 36^{\circ }={{\sqrt {5}}+1 \over 4}=\varphi /2$

$\sin \left({\frac {\pi }{10}}\right)=\sin 18^{\circ }={{\sqrt {5}}-1 \over 4}={\varphi -1 \over 2}={1 \over 2\varphi }$

Also see exact trigonometric constants.

Calculus

In calculus the relations stated below require angles to be measured in radians; the relations would become more complicated if angles were measured in another unit such as degrees. If the trigonometric functions are defined in terms of geometry, their derivatives can be found by verifying two limits. The first is:

$\lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1,$

verified using the unit circle and squeeze theorem. It may be tempting to propose to use L'Hôpital's rule to establish this limit. However, if one uses this limit in order to prove that the derivative of the sine is the cosine, and then uses the fact that the derivative of the sine is the cosine in applying L'Hôpital's rule, one is reasoning circularly—a logical fallacy. The second limit is:

$\lim _{x\rightarrow 0}{\frac {1-\cos x}{x}}=0,$

verified using the identity tan(x/2) = (1 − cos x)/sin x. Having established these two limits, one can use the limit definition of the derivative and the addition theorems to show that (sin x)′ = cos x and (cos x)′ = −sin x. If the sine and cosine functions are defined by their Taylor series, then the derivatives can be found by differentiating the power series term-by-term.

${d \over dx}\sin x=\cos x$

The rest of the trigonometric functions can be differentiated using the above identities and the rules of differentiation:

${\begin{matrix}{d \over dx}\sin x=&\cos x,&{d \over dx}\arcsin x=&{1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\cos x=&-\sin x,&{d \over dx}\arccos x=&{-1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\tan x=&\sec ^{2}x,&{d \over dx}\arctan x=&{1 \over 1+x^{2}}\\\\{d \over dx}\cot x=&-\csc ^{2}x,&{d \over dx}\operatorname {arccot} x=&{-1 \over 1+x^{2}}\\\\{d \over dx}\sec x=&\tan x\sec x,&{d \over dx}\operatorname {arcsec} x=&{1 \over |x|{\sqrt {x^{2}-1}}}\\\\{d \over dx}\csc x=&-\csc x\cot x,&{d \over dx}\operatorname {arccsc} x=&{-1 \over |x|{\sqrt {x^{2}-1}}}\end{matrix}}$

The integral identities can be found in "list of integrals of trigonometric functions". Some generic forms are listed below.

$\int {\frac {du}{\sqrt {a^{2}-u^{2}}}}=\sin ^{-1}\left({\frac {u}{a}}\right)+C$

$\int {\frac {du}{a^{2}+u^{2}}}={\frac {1}{a}}\tan ^{-1}\left({\frac {u}{a}}\right)+C$

$\int {\frac {du}{u{\sqrt {u^{2}-a^{2}}}}}={\frac {1}{a}}\sec ^{-1}\left|{\frac {u}{a}}\right|+C$

Implications

The fact that the differentiation of trigonometric functions (sine and cosine) results in linear combinations of the same two functions is of fundamental importance to many fields of mathematics, including differential equations and fourier transformations.

Exponential definitions

Function	Inverse Function
$\sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\,$	$\arcsin x=-i\ln \left(ix+{\sqrt {1-x^{2}}}\right)\,$
$\cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\,$	$\arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)\,$
$\tan \theta ={\frac {e^{i\theta }-e^{-i\theta }}{i(e^{i\theta }+e^{-i\theta })}}\,$	$\arctan x={\frac {i\ln \left({\frac {i+x}{i-x}}\right)}{2}}\,$
$\csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}\,$	$\operatorname {arccsc} x=-i\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,$
$\sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}\,$	$\operatorname {arcsec} x=-i\ln \left({\tfrac {1}{x}}+{\sqrt {1-{\tfrac {i}{x^{2}}}}}\right)\,$
$\cot \theta ={\frac {i(e^{i\theta }+e^{-i\theta })}{e^{i\theta }-e^{-i\theta }}}\,$	$\operatorname {arccot} x={\frac {i\ln \left({\frac {i-x}{i+x}}\right)}{2}}\,$
$\operatorname {cis} \,\theta =e^{i\theta }\,$	$\operatorname {arccis} \,x={\frac {\ln x}{i}}\,$

Miscellaneous

Dirichlet kernel

The Dirichlet kernel D_n(x) is the function occurring on both sides of the next identity:

$1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left[\left(n+{\frac {1}{2}}\right)x\right\rbrack }{\sin \left({\frac {x}{2}}\right)}}.$

The convolution of any integrable function of period 2π with the Dirichlet kernel coincides with the function's nth-degree Fourier approximation. The same holds for any measure or generalized function.

Extension of half-angle formulae

If we set

$t=\tan \left({\frac {x}{2}}\right),$

then

$\sin(x)={\frac {2t}{1+t^{2}}}{\text{ and }}\cos(x)={\frac {1-t^{2}}{1+t^{2}}}{\text{ and }}e^{ix}={\frac {1+it}{1-it}}.$

where e^ix is the same as cis(x). This substitution of t for tan(x/2), with the consequent replacement of sin(x) by 2t/(1 + t²) and cos(x) by (1 − t²)/(1 + t²) is useful in calculus for converting rational functions in sin(x) and cos(x) to functions of t in order to find their antiderivatives. For more information see tangent half-angle formula.