User:Bingjun Zhang/Wagner's gene network model
The Wagner's gene network model was first proposed by Andreas Wagner in 1996[1] and then used or extended/modified by other groups to study the evolution of gene network, gene expression, robustness, plasticity and epistasis[2][3][4]. The model and its variants explicitly modeled the developmental and evolutionary process of genetic regulatory networks.
Assumptions
[edit]The model and its variants have a number of simplifying assumptions. Three of them are listing below.
- The organisms are modeled as gene regulatory networks. The models assume that the gene expression is regulated exclusively on the transcriptional level;
- The product of one gene could be regulatory factor of itself or other genes. The models assume that one gene can only produce one active transcriptional regulator;
- The effects of one regulator act independently from other regulator of the same target gene.
Organisms
[edit]Gene Network
[edit]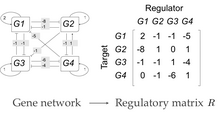
The unicellular organisms are modeled as regulatory gene networks with a number of interacting genes. The product of each gene can regulate the expression level of itself and/or the other genes through cis-regulatory elements. The interactions among genes constitute a gene network. The gene network is represented by a × regulatory matrix in the model. The elements in matrix R represent the interaction strength. Positive values in the matrix represent the active regulation of the target gene, negative ones represent repression.
Gene Expression
[edit]
Gene expression pattern of a organism at time is represented by a state vector
whose elements denotes the expression states of gene i at time t. In the original Wagner model,
∈
where 1 represents the gene is expressed while -1 is not. The expression pattern can only be ON or OFF. The continuous expression pattern between -1 (or 0) and 1 is also implemented in some other variants[2][3][4].
Development
[edit]The development process is modeled as the development of gene expression states. The gene expression pattern at time is defined as the initial expression state. Starting from the initial states, the interactions among genes will change the expression states during the development process. This process is modeled by the following difference equations
τσ
= σ
where τ) represents the expression state of at time t+τ. It is determined by a filter function σ. represents the weighted sum of regulatory effects () of all genes on gene at time t. In the original Wagner model, the filter function is a step function
σ if if if
In other variants, the filter function is implemented as a sigmoidal function
σ
In this way, the expression states will acquire a continuous but not discret states. The gene expression will reach the final state if it reach a stable pattern.
Evolutionary Simulation
[edit]With this model, a population with multiple organisms can be created and evolved from generation to generation.
Mutation
[edit]Mutations are modeled as the changes in gene regulation, i.e., the changes of the elements in the regulatory matrix .
Reproduction
[edit]Both sexual and asexual reproductions are implemented. The asexual reproduction is implemented as producing the offspring's genome (the gene network) by directly copying the parent's genome. Sexual reproduction is implemented as the recombination of the two parents' genome.
Selection
[edit]The organisms are considered to be viable if they reach the stable gene expression pattern but not oscillation. An organism with oscillated expression pattern will be discarded and can not enter the next generation.
References
[edit]- ^ Wagner A (1996). "Does Evolutionary Plasticity Evolve?", Evolution, 50(3):1008-1023.
- ^ a b Bergman A and Siegal ML (2003). "Evolutionary capacitance as a general feature of complex gene networks", Nature, 424(6948):549-552.
- ^ a b Azevedo RBR., Lohaus R and Srinivasan S and Dang KK and Burch CL (2006). "Sexual reproduction selects for robustness and negative epistasis in artificial gene networks", Nature, 440(7080):87-90.
- ^ a b Huerta-Sanchez E, Durrett R (2007). "Wagner's canalization model", Theoretical Population Biology, 71(2):121-130.













![{\displaystyle [\sum _{j=1}^{N}w_{ij}S_{j}(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1c221147021d92685ce8a5b9b69e350c45da33e)
}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dc77a4d3a47a1b4d1a55354a15bf6028fb5c143)









