Jump to content

User:Bernanke's Crossbow/sandbox/Polyhedral skeletal electron pair theory

From Wikipedia, the free encyclopedia
The butterfly cluster compound [Re4(CO)12]2− conforms to PSEPT.

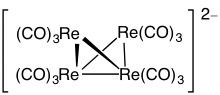
In chemistry, polyhedral skeletal electron pair theory (PSEPT) is a set of empirical regularities describing the number of electrons necessary to form a cluster compound in a specified geometry. The rules developed as a generalization of patterns in borane and carborane clusters,[citation needed] but have a molecular orbital rationalization[1][2][3] and apply to elements across the periodic table.

Historically, PSEPT was originally formulated by Kenneth Wade.[4] It has been further developed Michael Mingos[5][6] and E. D. Jemmis. It is thus sometimes known as Wade's rules, the Wade–Mingos rules,[7] or Jemmis mno rules.[8][9][10]

The Jemmis mno rules reduce to Hückel's rule when restricted to two dimensions and reduce to Wade's rules when restricted to one polyhedron.[11]

Predicting structures of cluster compounds

[edit]
Pb2−
10
(BH)7−
7

The polyhedral cluster compounds poorly described by classical Lewis structures have extensive delocalized bonding along the cluster skeleton. PSEPT begins with a skeletal electron count, which omits any electrons in extraskeletal bonds or lone pairs. For example, B7H2−
7 contains 30 electrons, but 14 are consumed in B–H σ bonds, leaving 16 skeletal electrons. Likewise, Pb2−
10 has 42 electrons, but 20 lie in lead's inert s orbital, leaving 12 skeletal electrons. TO DO: fix this example; should be closo In Rh6(CO)16, each CO ligand double-bonds to acts as a σ donor, giving 86 electrons, of which 60 fill each rhodium atoms' inert d shell, TO DO: backbonding? leaving 26 skeletal electrons.[citation needed]

Deltahedral case

[edit]

In the simplest case, there are a cluster atoms and roughly 2a skeletal electrons. In that case, PSEPT associates a polyhedron (tabulated below) with v vertices and all triangular faces (a deltahedron) to 2(v + 1) skeletal electrons.[12]

Number of vertices Polyhedron
4 Tetrahedron
5 Trigonal bipyramid
6 Octahedron
7 Pentagonal bipyramid
8 D2d (trigonal) dodecahedron (snub disphenoid)
9 Tricapped trigonal prism
10 Bicapped square antiprismatic molecular geometry
11 Edge-contracted icosahedron (octadecahedron)
12 Icosahedron (bicapped pentagonal antiprism)

If a ≥ v, then one atom is placed at each vertex of the polyhedron. Atoms try to adopt "normal" coordination numbers; thus larger and more electropositive atoms prefer higher-degree vertices. If a > v, then each surplus atom will act as an η3-ligand and cap a particular face. For example, Os6(CO)18 has only 12 skeletal electrons, corresponding to v = 5 and a trigonal bipyramid. The remaining osmium atom then caps one of the bipyramidal faces:

Os6(CO)18, carbonyls omitted
Os6(CO)18, carbonyls omitted

Likewise, in boron hydride clusters, each boron atom is at least tetracoordinate, and surplus hydrogen atoms are placed in open face positions to even out the coordination number of the vertices.

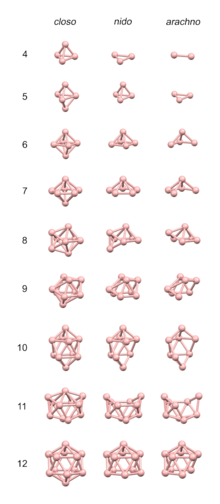
Ball-and-stick models showing the small boron hydride clusters' skeleta.

Typically, however, a < v. If a is only slightly smaller than v, then some vertices are left empty. Such structures have specialized nomenclatural prefixes:

Vacancy count Name Example
-1 (capped) hypercloso-
0 closo-
1 nido- ("nest-like") B
5H4−
5 (from octahedron)[13]		 B 5H4− 5
(hydrogen atoms omitted)
2 arachno- ("spider-like") S2+
4 (from octahedron)		 S2+ 4
C2B7H13
3 hypho-
4 klado- (TO DO: contradicted by boron hydride clusters)

In general, the vacancy occurs at the position most discordant with an atom's natural coordination geometry. Larger, more electropositive atoms leave low-degree vertices vacant; smaller, more electronegative atoms leave high-degree vertices vacant. If multiple vacancies are present, then their location depends on the atom size. Small atoms tend to adopt adjacent vacancies, whereas large atoms tend to adopt nonadjacent ones.

3c-2e bonds can capture the molecular orbital structure of clusters with at least one vacancy, but the bonding is more delocalized if there are few electrons.[14]

Compounds with more than two vacancies (e.g. hypho- or klado- structures) often adopt other forms. As Jemmis noted, the atoms may form multiple polyhedra fused along a face or single vertex, which are sometimes called a conjuncto- structure.[15] In that case, each sub-polyhedron substitutes for a vacancy (indeed, in the 2(v + 1) case, the " + 1" counts the entire-cluster polyhedron). However, as the electron-surfeit increases, eventually compounds begin to adopt a different shape altogether.

Cubic case

[edit]

If there are roughly 3 electrons per atom, then PSEPT proposes that the cluster should adopt the form of a polyhedron with cubic skeleton. These are sometimes called 3-connected polyhedra, although their 1‑skeleton is not triconnected.

Rather than adopting structures based on deltahedra, the 5n-type clusters have structures based on a different series of polyhedra known as the 3-connected polyhedra, in which each vertex is connected to 3 other vertices. The 3-connected polyhedra are the duals of the deltahedra. The common types of 3-connected polyhedra are listed below.

5n cluster: P4
5n + 3 cluster: P4S3
5n + 6 cluster: P4O6
Number of vertices Type of 3-connected polyhedron
4 Tetrahedron
6 Trigonal prism
8 Cube
10 Pentagonal prism
12 D2d pseudo-octahedron (dual of snub disphenoid)
14 Dual of triaugmented triangular prism (K5 associahedron)
16 Square truncated trapezohedron
18 Dual of edge-contracted icosahedron
20 Dodecahedron

The 5n rules are as follows.

Total electron count Predicted structure
5n n-vertex 3-connected polyhedron
5n + 1 n – 1 vertex 3-connected polyhedron with one vertex inserted into an edge
5n + 2 n – 2 vertex 3-connected polyhedron with two vertices inserted into edges
5n + k n − k vertex 3-connected polyhedron with k vertices inserted into edges

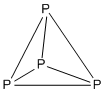
Example: P4

Electron count: 4 × P = 4 × 5 = 20
It is a 5n structure with n = 4, so it is tetrahedral

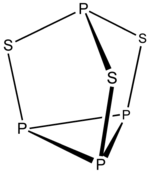
Example: P4S3

Electron count 4 × P + 3 × S = 4 × 5 + 3 × 6 = 38
It is a 5n + 3 structure with n = 7. Three vertices are inserted into edges

Example: P4O6

Electron count 4 × P + 6 × O = 4 × 5 + 6 × 6 = 56
It is a 5n + 6 structure with n = 10. Six vertices are inserted into edges

6n rules

[edit]

As more electrons are added to a 5n cluster, the number of electrons per vertex approaches 6. Instead of adopting structures based on 4n or 5n rules, the clusters tend to have structures governed by the 6n rules, which are based on rings. The rules for the 6n structures are as follows.

S8 crown
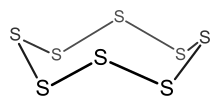
Total electron count Predicted structure
6n – k n-membered ring with k⁄2 transannular bonds
6n – 4 n-membered ring with 2 transannular bonds
6n – 2 n-membered ring with 1 transannular bond
6n n-membered ring
6n + 2 n-membered chain (n-membered ring with 1 broken bond)

Example: S8

Electron count = 8 × S = 8 × 6 = 48 electrons.
Since n = 8, 6n = 48, so the cluster is an 8-membered ring.
6n + 2 cluster: hexane

Hexane (C6H14)

Electron count = 6 × C + 14 × H = 6 × 4 + 14 × 1 = 38
Since n = 6, 6n = 36 and 6n + 2 = 38, so the cluster is a 6-membered chain.

Isolobal vertex units

[edit]

Provided a vertex unit is isolobal with BH then it can, in principle at least, be substituted for a BH unit, even though BH and CH are not isoelectronic. The CH+ unit is isolobal, hence the rules are applicable to carboranes. This can be explained due to a frontier orbital treatment.[12] Additionally there are isolobal transition-metal units. For example, Fe(CO)3 provides 2 electrons. The derivation of this is briefly as follows:

  • Fe has 8 valence electrons.
  • Each carbonyl group is a net 2 electron donor after the internal σ- and π-bonding are taken into account making 14 electrons.
  • 3 pairs are considered to be involved in Fe–CO σ-bonding and 3 pairs are involved in π-backbonding from Fe to CO reducing the 14 to 2.

Bonding in cluster compounds

[edit]
closo-B
6H2−
6
MO diagram of B
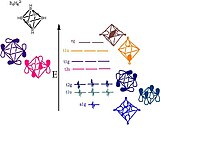
6H2−
6 showing the orbitals responsible for forming the cluster. Pictorial representations of the orbitals are shown; the MO sets of T and E symmetry will each have two or one additional pictorial representation, respectively, that are not shown here.
The boron atoms lie on each vertex of the octahedron and are sp hybridized.[13] One sp-hybrid radiates away from the structure forming the bond with the hydrogen atom. The other sp-hybrid radiates into the center of the structure forming a large bonding molecular orbital at the center of the cluster. The remaining two unhybridized orbitals lie along the tangent of the sphere like structure creating more bonding and antibonding orbitals between the boron vertices.[9] The orbital diagram breaks down as follows:
The 18 framework molecular orbitals, (MOs), derived from the 18 boron atomic orbitals are:
  • 1 bonding MO at the center of the cluster and 5 antibonding MOs from the 6 sp-radial hybrid orbitals
  • 6 bonding MOs and 6 antibonding MOs from the 12 tangential p-orbitals.
The total skeletal bonding orbitals is therefore 7, i.e. n + 1.

Transition metal clusters

[edit]

Transition metal clusters use the d orbitals for bonding. Thus, they have up to nine bonding orbitals, instead of only the four present in boron and main group clusters.[16][17] PSEPT also applies to metallaboranes

Clusters with interstitial atoms

[edit]

Owing their large radii, transition metals generally form clusters that are larger than main group elements. One consequence of their increased size, these clusters often contain atoms at their centers. A prominent example is [Fe6C(CO)16]2-. In such cases, the rules of electron counting assume that the interstitial atom contributes all valence electrons to cluster bonding. In this way, [Fe6C(CO)16]2- is equivalent to [Fe6(CO)16]6- or [Fe6(CO)18]2-.[18]

Second article starts here

[edit]

Electron-counting rules

[edit]

Electron-counting rules are used to predict the preferred electron count for molecules. The octet rule, the 18-electron rule, and Hückel's 4n + 2 pi-electron rule are proven to be useful in predicting the molecular stability. Wade's rules were formulated to explain the electronic requirement of monopolyhedral borane clusters. The Jemmis mno rules are an extension of Wade's rules, generalized to include condensed polyhedral boranes as well.

The first condensed polyhedral borane, B20H16, is formed by sharing four vertices between two icosahedra. According to Wade's n + 1 rule for n-vertex closo structures, B20H16 should have a charge of +2 (n + 1 = 20 + 1 = 21 pairs required; 16 BH units provide 16 pairs; four shared boron atoms provide 6 pairs; thus 22 pairs are available). To account for the existence of B20H16 as a neutral species, and to understand the electronic requirement of condensed polyhedral clusters, a new variable, m, was introduced and corresponds to the number of polyhedra (sub-clusters).[19] In Wade's n + 1 rule, the 1 corresponds to the core bonding molecular orbital (BMO) and the n corresponds to the number of vertices, which in turn is equal to the number of tangential surface BMOs. If m polyhedra condense to form a macropolyhedron, m core BMOs will be formed. Thus the skeletal electron pair (SEP) requirement of closo-condensed polyhedral clusters is m + n.

Single-vertex sharing is a special case where each subcluster needs to satisfy Wade's rule separately. Let a and b be the number of vertices in the subclusters including the shared atom. The first cage requires a + 1 and the second cage requires b + 1 SEPs. Therefore, a total of a + b + 2 or a + b + m SEPs are required; but a + b = n + 1, as the shared atom is counted twice. The rule can be modified to m + n + 1, or generally m + n + o, where o corresponds to the number of single-vertex sharing condensations. The rule can be made more general by introducing a variable, p, corresponding to the number of missing vertices, and q, the number of caps. As such, the generalized Jemmis rule can be stated as follows:

The SEP requirement of condensed polyhedral clusters is m + n + o + p − q, where m is the number of subclusters, n is the number of vertices, o is the number of single-vertex shared condensations, p is the number of missing vertices and q is the number of caps.[20][21]

Examples

[edit]

B20H16

[edit]
Condensed polyhedral boranes and metallaboranes

m + n + o + p − q = 2 + 20 + 0 + 0 + 0 = 22 SEPs are required; 16 BH units provide 16 pairs; four shared boron atoms provide 6 pairs, which describes why B20H16 is stable as a neutral species.[21]

B21H−
18

[edit]

closo-B21H−18 is formed by the face-sharing condensation of two icosahedra. The m + n + o + p − q rule demands 23 SEPs; 18 BH units provide 18 pairs and 3 shared boron atoms provide 4+1⁄2 pairs; the negative charge provides one half pair.[22]

B12H16

[edit]

The bis-nido-B12H16 is formed by the edge-sharing condensation of a nido-B8 unit and a nido-B6 unit. The m + n + o + p − q count of 16 SEPs are satisfied by ten BH units which provide 10 pairs, two shared boron atoms which provide 3 pairs, and six bridging H atoms which provide 3 pairs.[21]

Cu(B11H11)3−
2

[edit]

m + n + o + p − q = 26 SEPs. A transition metal with n valence electrons provides n − 6 electrons for skeletal bonding as 6 electrons occupying the metal-like orbitals do not contribute much to the cluster bonding. Therefore Cu provides 2+1⁄2 pairs, 22 BH units provide 22 pairs; three negative charges provide 1+1⁄2 pairs.[21]

Ferrocene

[edit]
Ferrocene

According to the m + n + o + p − q rule, ferrocene requires 2 + 11 + 1 + 2 − 0 = 16 SEPs. 10 CH units provide 15 pairs while Fe provides one pair. [21]

B18H2−
20

[edit]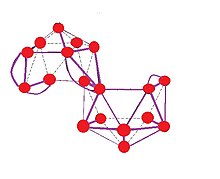
B18H2−20, hydrogens removed

B18H2−20 is a bis-nido edge-shared polyhedron. Here, m + n + o + p − q = 2 + 18 + 0 + 2 − 0 = 22; 16 BH units provide 16 pairs, 4 bridging hydrogen atoms provide 2 pairs, two shared boron atoms provide 3 pairs, along with the two negative charges which provide 1 pair.[21]

Triple-decker complexes

[edit]

Triple-decker complexes are known to obey a 30-valence electron (VE) rule. Subtracting 6 pairs of nonbonding electrons from the two metal atoms brings the number of SEPs to 9 pairs. For a triple-decker complex with C5H5 as the decks, m + n + o + p − q = 3 + 17 + 2 + 2 − 0 = 24. Subtracting the 15 pairs corresponding to C–C sigma bonds, it becomes 9 pairs. For example, consider (C5(CH3)5)3Ru+2: 15 C–CH3 groups provide 22+1⁄2 pairs. Each ruthenium atom provides one pair. Removing the electron corresponding to the positive charge of the complex leads to a total of 22+1⁄2 + 2 − 1⁄2 = 24 pairs.

β-Rhombohedral boron

[edit]
B105, conceptually fragmented to B57 and B48.

The structure of β-rhombohedral boron is complicated by the presence of partial occupancies and vacancies.[23][24][25] The idealized unit cell, B105 has been shown to be electron-deficient and hence metallic according to theoretical studies, but β-boron is a semiconductor.[26] Application of the Jemmis rule shows that the partial occupancies and vacancies are necessary for electron sufficiency.

B105 can be conceptually divided into a B48 fragment and a B28−B−B28 (B57) fragment. According to Wade's rule, the B48 fragment requires 8 electrons (the icosahedron at the centre (green) requires 2 electrons; each of the six pentagonal pyramids (black and red) completes an icosahedron in the extended structure; as such the electronic requirement for each of them is 1). The B28−B−B28 or B57 is formed by the condensation of 6 icosahedra and two trigonal bipyramids. Here, m + n + o + p − q = 8 + 57 + 1 + 0 − 0 = 66 pairs required for stability, but 67+1⁄2 are available. Therefore the B28−B−B28 fragment has 3 excess electrons and the idealized B105 is missing 5 electrons. The 3 excess electrons in the B28−B−B28 fragment can be removed by removing one B atom, which leads to B27−B−B28 (B56). The requirement of 8 electrons by the B48 fragment can be satisfied by 2+2⁄3 boron atoms and the unit cell contains 48 + 56 + 2+2⁄3 = 106+2⁄3, which is very close to the experimental result.[10]

See Also

[edit]

References

[edit]
  1. ^ Wade, K. (1976). "Structural and Bonding Patterns in Cluster Chemistry". Adv. Inorg. Chem. Radiochem. Advances in Inorganic Chemistry and Radiochemistry. 18: 1–66. doi:10.1016/S0065-2792(08)60027-8. ISBN 9780120236183.
  2. ^ Gilespie, R. J. (1979). "Nyholm Memorial Lectures". Chem. Soc. Rev. 8 (3): 315–352. doi:10.1039/CS9790800315.
  3. ^ Mingos, D. M. P. (1984). "Polyhedral Skeletal Electron Pair Approach". Acc. Chem. Res. 17 (9): 311–319. doi:10.1021/ar00105a003.
  4. ^ Wade, K. (1971). "The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds". J. Chem. Soc. D. 1971 (15): 792–793. doi:10.1039/C29710000792.
  5. ^ Mingos, D. M. P. (1972). "A General Theory for Cluster and Ring Compounds of the Main Group and Transition Elements". Nature Physical Science. 236 (68): 99–102. Bibcode:1972NPhS..236...99M. doi:10.1038/physci236099a0.
  6. ^ Mingos, D. M. P (1984). "Polyhedral skeletal electron pair approach". Acc. Chem. Res. 17 (9): 311–319. doi:10.1021/ar00105a003.
  7. ^ Welch, Alan J. (2013). "The significance and impact of Wade's rules". Chem. Commun. 49 (35): 3615–3616. doi:10.1039/C3CC00069A. PMID 23535980.
  8. ^ Jemmis, Eluvathingal D.; Balakrishnarajan, Musiri M.; Pancharatna, Pattath D. (2001). "A Unifying Electron-counting rule for Macropolyhedral Boranes, Metallaboranes, and Metallocenes". J. Am. Chem. Soc. 123 (18): 4313–4323. doi:10.1021/ja003233z. PMID 11457198.
  9. ^ a b Jemmis, Eluvathingal D.; Balakrishnarajan, Musiri M.; Pancharatna, Pattath D. (2002). "Electronic Requirements for Macropolyhedral Boranes". Chem. Rev. 102 (1): 93–144. doi:10.1021/cr990356x. PMID 11782130.
  10. ^ a b Jemmis, E. D.; Balakrishnarajan, M. M. (2001). "Polyhedral Boranes and Elemental Boron: Direct Structural Relations and Diverse Electronic Requirements". J. Am. Chem. Soc. 123 (18): 4324–4330. doi:10.1021/ja0026962. PMID 11457199.
  11. ^ Jemmis, E. D.; Jayasree, E. G. (2003). "Analogies between Boron and Carbon". Acc. Chem. Res. 36 (11): 816–824. doi:10.1021/ar0300266. PMID 14622028.
  12. ^ a b Cotton, F. Albert; Wilkinson, Geoffrey; Murillo, Carlos A.; Bochmann, Manfred (1999), Advanced Inorganic Chemistry (6th ed.), New York: Wiley-Interscience, ISBN 0-471-19957-5
  13. ^ a b Cotton, Albert (1990). Chemical Applications of Group Theory. John Wiley & Sons. pp. 205–251. ISBN 0-471-51094-7.
  14. ^ Greenwood & Earnshaw 1984, pp. 179–183.
  15. ^ Greenwood & Earnshaw 1984, p. 171.
  16. ^ King, R. B.; Rouvray, D. H. (1977). "Chemical Applications of Group Theory and Topology.7. A Graph-Theoretical Interpretation of the Bonding Topology in Polyhedral Boranes, Carboranes, and Metal Clusters". J. Am. Chem. Soc. 99 (24): 7834–7840. doi:10.1021/ja00466a014.
  17. ^ Kostikova, G. P.; Korolkov, D. V. (1985). "Electronic Structure of Transition Metal Cluster Complexes with Weak- and Strong-field Ligands". Russ. Chem. Rev. 54 (4): 591–619. Bibcode:1985RuCRv..54..344K. doi:10.1070/RC1985v054n04ABEH003040. S2CID 250797537.
  18. ^ Fehlner, Thomas P. (2006). "Cluster Compounds: Inorganometallic Compounds Containing Transition Metal & Main Group Elements". Encyclopedia of Inorganic Chemistry. doi:10.1002/0470862106.ia097. ISBN 0470860782.
  19. ^ Jemmis, E. D.; Balakrishnarajan, M. M. (2000). "Electronic Requirements of Polycondensed Polyhedral Boranes". J. Am. Chem. Soc. 122 (18): 4516–4517. doi:10.1021/ja994199v.
  20. ^ Jemmis, E. D.; Balakrishnarajan, M. M.; Pancharatna, P. D. (2001). "A Unifying Electron-Counting Rule for Macropolyhedral Boranes, Metallaboranes, and Metallocenes". J. Am. Chem. Soc. 123 (18): 4313–4323. doi:10.1021/ja003233z. PMID 11457198.
  21. ^ a b c d e f Jemmis, E. D.; Balakrishnarajan, M. M.; Pancharatna, P. D. (2002). "Electronic Requirements for Macropolyhedral Boranes". Chem. Rev. 102 (1): 93–144. doi:10.1021/cr990356x. PMID 11782130.
  22. ^ Bernhardt, E.; Brauer, D. J.; Finze, M.; Willner, H. (2007). "closo-[B21H18]−: A Face-Fused Diicosahedral Borate Ion". Angew. Chem. Int. Ed. Engl. 46 (16): 2927–2930. doi:10.1002/anie.200604077. PMID 17366499.
  23. ^ Hughes, R. E.; Kennard, C. H. L.; Sullenger, D. B.; Weakliem, H. A.; Sands, D. E.; Hoard, J. L. (1963). "The Structure of β-Rhombohedral Boron". J. Am. Chem. Soc. 85 (3): 361–362. doi:10.1021/ja00886a036.
  24. ^ Hoard, J. L.; Sullenger, D. B.; Kennard, C. H. L.; Hughes, R. E. (1970). "The structure analysis of β-rhombohedral boron". J. Solid State Chem. 1 (2): 268–277. Bibcode:1970JSSCh...1..268H. doi:10.1016/0022-4596(70)90022-8.
  25. ^ Slack, G. A.; Hejna, C. I.; Garbauskas, M. F.; Kasper, J. S. (1988). "The crystal structure and density of β-rhombohedral boron". J. Solid State Chem. 76 (1): 52–63. Bibcode:1988JSSCh..76...52S. doi:10.1016/0022-4596(88)90192-2.
  26. ^ Prasad, D. L. V. K; Balakrishnarajan, M. M.; Jemmis, E. D. (2005). "Electronic structure and bonding of β-rhombohedral boron using cluster fragment approach". Phys. Rev. B. 72 (19): 195102. Bibcode:2005PhRvB..72s5102P. doi:10.1103/physrevb.72.195102.

General references

[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=User:Bernanke%27s_Crossbow/sandbox/Polyhedral_skeletal_electron_pair_theory&oldid=1263117999"