User:BARRY.ismael/sandbox

Graphe de distance unitaire

[[Fichier : Unit distance 16 40.svg|thumb|Un graphique de distance unitaire avec 16 sommets et 40 arêtes]

En mathématiques, particulièrement en théorie des graphes géométriques, un graphe de distance unitaire est un graphe formé à partir d'une collection de points dans le plan euclidien en reliant deux points lorsque la distance qui les sépare est exactement égale à un. Pour distinguer ces graphes d'une définition plus large qui permet à certains couples de sommets non adjacents d'être à une distance de un, on peut également les appeler graphes de distance unitaire stricte ou graphes de distance unitaire fidèles. En tant que famille héréditaire de graphes, ils peuvent être caractérisés par des sous-graphes interdits. Les graphes de distance unitaire incluent les graphes cactus, les graphes allumettes, les graphes de pièces de monnaie, et les graphes hypercubes. Les graphes de Petersen généralisés sont des graphes de distance unitaire non stricts.

Un problème non résolu de Paul Erdős consiste à déterminer combien d'arêtes un graphe de distance unitaire avec $n$ sommets peut avoir. La meilleure borne inférieure connue est légèrement supérieure à linéaire en $n$ — bien loin de la borne supérieure, proportionnelle à $n^{4/3}$. Le nombre de couleurs nécessaires pour colorier les graphes de distance unitaire est également inconnu (le problème de Hadwiger–Nelson) : certains graphes de distance unitaire nécessitent cinq couleurs, et chaque graphe de distance unitaire peut être colorié avec sept couleurs. Pour tout nombre algébrique, il existe un graphe de distance unitaire avec deux sommets séparés par cette distance. Selon le théorème de Beckman-Quarles, les seules transformations du plan qui préservent tous les graphes de distance unitaire sont les isométries du plan euclidien.

Il est possible de construire efficacement un graphe de distance unitaire, étant donné ses points. Trouver toutes les distances unitaires a des applications en recherche de motifs, où cela peut être une première étape pour identifier des copies congruentes de motifs plus grands. Cependant, déterminer si un graphe donné peut être représenté comme un graphe de distance unitaire est un problème NP-difficile, et plus précisément complet pour la théorie existentielle des réels.

Définition

Le graphe de Petersen en tant que graphe de distance unitaire

Le graphe de Möbius–Kantor comme sous-graphe d'un graphe de distance unitaire

Le graphe de distance unitaire pour un ensemble de points dans le plan est le graphe non orienté ayant ces points comme sommets, avec une arête entre deux sommets lorsque leur distance euclidienne est exactement égale à un. Un graphe abstrait est dit être un graphe de distance unitaire s’il est possible de trouver des emplacements distincts dans le plan pour ses sommets, de sorte que ses arêtes aient une longueur unitaire et que tous les couples de sommets non adjacents soient à une distance différente de l’unité. Lorsque cela est possible, le graphe abstrait est isomorphe au graphe de distance unitaire des emplacements choisis. Alternativement, certaines sources utilisent une définition plus large, permettant aux paires de sommets non adjacents d'être à une distance unitaire. Les graphes résultants sont les sous-graphes des graphes de distance unitaire (tels que définis ici). Lorsque la terminologie peut prêter à confusion, les graphes dans lesquels les non-arêtes doivent être à une distance différente de l'unité peuvent être appelés graphes de distance unitaire stricte ou graphes de distance unitaire fidèles. Les sous-graphes des graphes de distance unitaire sont, de manière équivalente, les graphes pouvant être dessinés dans le plan en n'utilisant qu'une seule longueur d'arête. Par souci de brièveté, cet article se réfère à ceux-ci comme "graphes de distance unitaire non stricts".

Les graphes de distance unitaire ne doivent pas être confondus avec les graphes de disque unitaire, qui connectent les paires de points lorsque leur distance est inférieure ou égale à un, et sont fréquemment utilisés pour modéliser les réseaux de communication sans fil.

Exemples

Le graphe complet sur deux sommets est un graphe de distance unitaire, tout comme le graphe complet sur trois sommets (le graphe triangulaire), mais ce n'est pas le cas pour le graphe complet sur quatre sommets. En généralisant le graphe triangulaire, tout graphe cyclique est un graphe de distance unitaire, réalisé par un polygone régulier. Deux graphes finis de distance unitaire, connectés par un seul sommet partagé, produisent un autre graphe de distance unitaire, car l'un peut être tourné par rapport à l'autre pour éviter des distances unitaires supplémentaires indésirables. En connectant ainsi des graphes, tout arbre fini ou graphe cactus peut être réalisé comme un graphe de distance unitaire.

Le graphe hypercube $Q_{4}$ a 16 sommets et 32 distances unitaires

Le graphe de Hamming $H(3,3)$ a 27 sommets et 81 distances unitaires

Tout produit cartésien de graphes de graphes de distance unitaire produit un autre graphe de distance unitaire ; cependant, ceci n'est pas vrai pour d'autres produits courants de graphes. Par exemple, le produit fort de graphes, appliqué à deux graphes non vides, produit des sous-graphes complets avec quatre sommets, qui ne sont pas des graphes de distance unitaire. Les produits cartésiens de graphes chemins forment des graphes en grille de toute dimension ; les produits cartésiens du graphe complet sur deux sommets forment les graphes hypercubes, et les produits cartésiens de graphes triangulaires forment les graphes de Hamming $H(d,3)$.

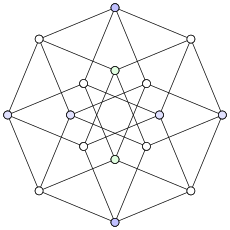
D'autres graphes spécifiques qui sont des graphes de distance unitaire incluent le graphe de Petersen, le graphe de Heawood, le graphe roue $W_{7}$ (le seul graphe roue qui est un graphe de distance unitaire), ainsi que la broche de Moser et le graphe de Golomb (petits graphes de distance unitaire 4-chromatiques). Tous les graphes de Petersen généralisés, tels que le graphe de Möbius–Kantor représenté, sont des graphes de distance unitaire non stricts.

Les graphes allumettes sont un cas particulier de graphes de distance unitaire, dans lesquels aucune arête ne se croise. Chaque graphe allumette est un graphe planaire, mais certains graphes de distance unitaire planaires, comme la broche de Moser, ont un croisement dans chaque représentation en tant que graphe de distance unitaire. De plus, dans le contexte des graphes de distance unitaire, le terme "planaire" doit être utilisé avec précaution, car certains auteurs l’utilisent pour faire référence au plan dans lequel les distances unitaires sont définies, plutôt qu’à une interdiction de croisements. Les graphes de pièces de monnaie sont un cas encore plus particulier de graphes de distance unitaire et de graphes allumettes, dans lesquels chaque paire de sommets non adjacents est à une distance supérieure à une unité.

Propriétés

Nombre d'arêtes

{voir aussi|Problème des distances distinctes d'Erdős} {non résolu|mathématiques|Combien de distances unitaires peuvent être déterminées par un ensemble de $n$ points ?} Paul Erdős (1946) a posé la question d'estimer combien de paires de points dans un ensemble de $n$ points peuvent être à une distance unitaire l'un de l'autre. En termes de théorie des graphes, la question interroge sur la densité maximale d'un graphe de distance unitaire, et la publication d'Erdős à ce sujet est l'une des premières contributions à la théorie extrémale des graphes. Les graphes hypercubes et graphes de Hamming fournissent une borne inférieure sur le nombre de distances unitaires, proportionnelle à $n\log n.$ En considérant les points d'une grille carrée avec un espacement soigneusement choisi, Erdős a trouvé une borne inférieure améliorée sous la forme $$n^{1+c/\log \log n}$$ pour une constante $c$, et a offert $500 pour une démonstration de savoir si le nombre de distances unitaires peut également être borné par une fonction de cette forme. La meilleure borne supérieure connue pour ce problème est $${\sqrt[{3}]{\frac {29n^{4}}{4}}}\approx 1.936n^{4/3}.$$ Cette borne peut être interprétée comme comptant les incidences entre points et cercles unitaires, et est étroitement liée à l'inégalité du nombre de croisements et au théorème de Szemerédi–Trotter sur les incidences entre points et droites.

Pour de petites valeurs de $n$, le nombre maximum exact possible d'arêtes est connu. Pour $n=2,3,4,\dots$, ces nombres d'arêtes sont :

1, 3, 5, 7, 9, 12, 14, 18, 20, 23, 27, 30, 33, ... (sequence A186705 in the OEIS)

Sous-graphes interdits

Si un graphe donné $G$ n'est pas un graphe de distance unitaire non strict, aucun supergraphe $H$ de $G$ ne l'est. Un principe similaire s'applique aux graphes de distance unitaire stricts, mais en utilisant le concept de sous-graphe induit, un sous-graphe formé de toutes les arêtes entre les paires de sommets d'un sous-ensemble donné de sommets. Si $G$ n'est pas un graphe de distance unitaire strict, alors aucun autre $H$ ayant $G$ comme sous-graphe induit ne l'est. En raison de ces relations entre le statut de sous-graphe ou de supergraphe d'un graphe de distance unitaire, il est possible de décrire les graphes de distance unitaire par leurs sous-graphes interdits. Ce sont les graphes minimaux qui ne sont pas des graphes de distance unitaire du type donné. Ils permettent de déterminer si un graphe donné $G$ est un graphe de distance unitaire de l'un ou l'autre type. $G$ est un graphe de distance unitaire non strict si, et seulement si, $G$ n'est pas un supergraphe d'un graphe interdit pour les graphes de distance unitaire non stricts. $G$ est un graphe de distance unitaire strict si, et seulement si, $G$ n'est pas un supergraphe induit d'un graphe interdit pour les graphes de distance unitaire stricts.

Pour les graphes de distance unitaire non stricts et stricts, les graphes interdits incluent à la fois le graphe complet $K_{4}$ et le graphe biparti complet $K_{2,3}$. Pour $K_{2,3}$, quel que soit l'emplacement des sommets du côté à deux sommets de ce graphe, il y a au plus deux positions à une distance unitaire d'eux pour placer les trois autres sommets, donc il est impossible de placer les trois sommets aux points distincts. Ce sont les deux seuls graphes interdits pour les graphes de distance unitaire non stricts jusqu'à cinq sommets ; il existe six graphes interdits jusqu'à sept sommets et 74 pour des graphes jusqu'à neuf sommets. En raison du fait que coller deux graphes de distance unitaire (ou leurs sous-graphes) par un sommet produit des graphes de distance unitaire stricts (ou non stricts respectivement), chaque graphe interdit est un graphe biconnexe, qui ne peut pas être formé par ce processus de collage.

Le graphe roue $W_{7}$ peut être réalisé comme un graphe de distance unitaire strict avec six de ses sommets formant un hexagone régulier unitaire et le septième au centre de l'hexagone. Retirer l'une des arêtes du sommet central produit un sous-graphe qui possède toujours des arêtes de longueur unitaire, mais qui n'est pas un graphe de distance unitaire strict. La disposition en hexagone régulier de ses sommets est la seule façon (à congruence près) de placer les sommets en des points distincts de telle manière que les sommets adjacents soient à une distance unitaire, et cette disposition place également les deux extrémités de l'arête manquante à une distance unitaire. Par conséquent, c'est un graphe interdit pour les graphes de distance unitaire stricts, mais ce n'est pas l'un des six graphes interdits pour les graphes de distance unitaire non stricts. D'autres exemples de graphes qui sont des graphes de distance unitaire non stricts mais pas des graphes de distance unitaire stricts incluent le graphe formé en retirant une arête extérieure de $W_{7}$ et le graphe à six sommets formé à partir d'un prisme triangulaire en retirant une arête de l'un de ses triangles.

Nombres algébriques et rigidité

{article principal|Théorème de Beckman–Quarles} Pour chaque nombre algébrique $\alpha$, il est possible de construire un graphe de distance unitaire $G$ dans lequel une paire de sommets sont à une distance $\alpha$ dans toutes les représentations de distance unitaire de $G$. Ce résultat implique une version finie du théorème de Beckman–Quarles : pour tous deux points $p$ et $q$ situés à une distance $\alpha$ l'un de l'autre, il existe un graphe de distance unitaire rigide fini contenant $p$ et $q$ tel que toute transformation du plan qui conserve les distances unitaires dans ce graphe conserve également la distance entre $p$ et $q$. Le théorème complet de Beckman–Quarles stipule que les seules transformations du plan euclidien (ou d'un espace euclidien de dimension supérieure) qui conservent les distances unitaires sont les isométries. En d'autres termes, pour le graphe de distance unitaire infini engendré par tous les points du plan, tous les automorphismes de graphe préservent toutes les distances dans le plan, et pas seulement les distances unitaires.

Si $\alpha$ est un nombre algébrique de module 1 qui n'est pas une racine de l'unité, alors les combinaisons entières de puissances de $\alpha$ forment un sous-groupe de type fini du groupe additif des nombres complexes dont le graphe de distance unitaire a un degré infini. Par exemple, $\alpha$ peut être choisi comme l'une des deux racines complexes du polynôme $z^{4}-z^{3}-z^{2}-z+1$, produisant un graphe de distance unitaire de degré infini avec quatre générateurs.

Coloration

{article principal|Problème de Hadwiger–Nelson} {non résolu|mathématiques|Quel est le plus grand nombre chromatique possible d'un graphe de distance unitaire ?} Le problème de Hadwiger–Nelson concerne le nombre chromatique des graphes de distance unitaire, et plus particulièrement du graphe de distance unitaire infini formé de tous les points du plan euclidien. Par le théorème de De Bruijn–Erdős, qui suppose l'axiome du choix, cela équivaut à demander le plus grand nombre chromatique d'un graphe de distance unitaire fini. Il existe des graphes de distance unitaire nécessitant cinq couleurs dans toute coloration propre, et tous les graphes de distance unitaire peuvent être colorés avec au plus sept couleurs.

[[Fichier:Hadwiger-Nelson.svg|thumb|upright|Une coloration en sept couleurs du graphe de distance unitaire infini formé de tous les points du plan, et la fuseau de Moser, qui est un graphe de distance unitaire à nombre chromatique quatre, représentée comme un graphe de distance unitaire]] En réponse à une autre question de Paul Erdős, il est possible pour des graphes de distance unitaire sans triangles de nécessiter quatre couleurs.

Énumération

Le nombre de graphes de distance unitaire stricts sur $n\geq 4$ sommets étiquetés est au plus $${\binom {n(n-1)}{2n}}=O\left(2^{{\bigl (}4+o(1){\bigr )}n\log _{2}n}\right),$$ exprimé en utilisant la notation O et la notation o.

Généralisation aux dimensions supérieures

La définition d'un graphe de distance unitaire peut naturellement être généralisée à tout espace euclidien de dimension supérieure. En trois dimensions, les graphes de distance unitaire de $n$ points ont au plus $n^{3/2}\beta (n)$ arêtes, où $\beta$ est une fonction croissant très lentement, reliée à l'inverse de la fonction d'Ackermann. Ce résultat conduit à une borne similaire sur le nombre d'arêtes des graphes de voisinage relatif en trois dimensions. En quatre dimensions ou plus, tout graphe biparti complet est un graphe de distance unitaire, obtenu en plaçant les points sur deux cercles perpendiculaires ayant un centre commun, de sorte que les graphes de distance unitaire peuvent être des graphes denses. Les formules d'énumération pour les graphes de distance unitaire se généralisent aux dimensions supérieures et montrent qu'en quatre dimensions ou plus, le nombre de graphes de distance unitaire stricts est beaucoup plus grand que le nombre de sous-graphes des graphes de distance unitaire.

Tout graphe fini peut être plongé comme un graphe de distance unitaire dans un espace de dimension suffisamment élevée. Certains graphes peuvent nécessiter des dimensions très différentes pour les plongements en tant que graphes de distance unitaire non stricts et en tant que graphes de distance unitaire stricts. Par exemple, le graphe couronne à $2n$ sommets peut être plongé en quatre dimensions comme un graphe de distance unitaire non strict (c'est-à-dire de telle sorte que toutes ses arêtes aient une longueur unitaire). Cependant, il nécessite au moins $n-2$ dimensions pour être plongé en tant que graphe de distance unitaire strict, de sorte que ses arêtes soient les seules paires de sommets à distance unitaire. La dimension nécessaire pour réaliser un graphe donné en tant que graphe de distance unitaire strict est au plus deux fois son degré maximal.

Complexité computationnelle

La construction d'un graphe de distance unitaire à partir de ses points est une étape importante pour d'autres algorithmes visant à trouver des copies congruentes d'un motif dans un ensemble de points plus large. Ces algorithmes utilisent cette construction pour rechercher des positions candidates où l'une des distances du motif est présente, puis utilisent d'autres méthodes pour tester le reste du motif pour chaque candidat. Une méthode de Matoušek (1993) peut être appliquée à ce problème, donnant un algorithme pour trouver le graphe de distance unitaire d'un ensemble de points planaires en temps $n^{4/3}2^{O(\log ^{*}n)}$, où $\log ^{*}$ est la fonction logarithme itéré, qui croît lentement.

Il est NP-difficile—et plus précisément, complet pour la théorie existentielle des réels—de tester si un graphe donné est un graphe de distance unitaire (strict ou non strict) dans le plan. Il est également NP-complet de déterminer si un graphe de distance unitaire planaire possède un cycle hamiltonien, même lorsque les sommets du graphe ont tous des coordonnées entières connues.