User:Avronj/sandbox-sagnac

The Wang experiment

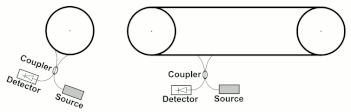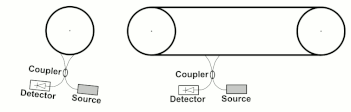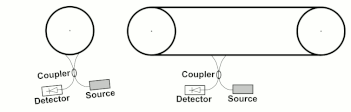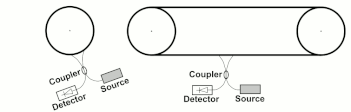
Modified versions of the Sganac experiment have been made by Wang et. al. in configurations similar to those shown in Fig. 5. The Wang interferometer does not move like a rigid body and Sagnac formula does not apply as the angular frequency ot rotation $\omega$ is not defined. Wang et. al. verified experimentally that a generalized Sagnac formula applies

$$\Delta \phi \approx {\frac {4\pi }{\lambda c}}\oint \mathbf {v} \cdot d\mathbf {x}$$

Figure 4. A Sagnac interferometer, shown on the left, versus a Wang interferometer shown on the right.

Theories

The shift in interference fringes in a ring interferometer is a consequence of the different times it takes a right and left moving light beams to complete a full round trip in the interferometer ring.

Relativistic derivation of Sagnac formula

Fig. 3: A closed optical fiber moving arbitrarily in space without stretching.

In a ring interferometer two counter-propagating light beams share a common optical path. It is convenient to think of the path as determined by a loop of an optical fiber , see Figure 3. The case of free space is recovered by taking the index of refraction $n$ of the fiber to be 1. The loop may have an arbitrary shape, and can move arbitrarily in space. The only restriction is that it is not allowed to stretch.

Consider a small segment of the fiber, whose length in its rest frame is $d\ell '$. The time intervals, $dt'_{\pm }$, it takes the left and right moving light rays to traverse the segment in the rest frame coincide and are given by$$dt'_{\pm }={n \over c}d\ell '$$Let ${\textstyle d\ell =|d\mathbf {x} |}$ be the length of this small segment in the lab frame. By the relativistic length contraction formula, ${\textstyle d\ell '=\gamma d\ell \approx d\ell }$ correct to first order in the velocity $\mathbf {v}$ of the segment. The time intervals $dt_{\pm }$ for traversing the segment in the lab frame are given by Lorentz transformation as:

$$dt_{\pm }=\gamma \left(dt'\pm {\frac {\mathbf {v} \cdot d\mathbf {x} '}{c^{2}}}\right)\approx {\frac {n}{c}}d\ell \pm {\frac {\mathbf {v} }{c^{2}}}\cdot d\mathbf {x}$$

correct to first order in the velocity $\mathbf {v}$. In general, the two beams will visit a given segment at slightly different times, but, in the absence of stretching, the length ${\textstyle d\ell }$ is the same for both beams.

It follows that the time difference for completing a cycle for the two beams is$$\Delta T=\int \left(dt_{+}-dt_{-}\right)\approx {\frac {2}{c^{2}}}\oint \mathbf {v} \cdot d\mathbf {x}$$Remarkably, the time difference is independent of the refraction index $n$ and the velocity of light in the fiber.

Imagine a screen for viewing fringes placed at the light source (alternatively, use a beamsplitter to send light from the source point to the screen). Given a steady light source, interference fringes will form on the screen with a fringe displacement given by ${\textstyle \Delta \phi \approx {\frac {2\pi c}{\lambda }}\Delta T}$ where the first factor is the frequency of light. This gives the generalized Sagnac formula $$\Delta \phi \approx {\frac {4\pi }{\lambda c}}\oint \mathbf {v} \cdot d\mathbf {x}$$In the special case that the fiber moves like a rigid body with angular frequency ${\boldsymbol {\omega }}$, the velocity is ${\textstyle \mathbf {v} ={\boldsymbol {\omega }}\times \mathbf {x} }$ and the line integral can be computed in terms of the area of the lop:$$\oint \mathbf {v} \cdot d\mathbf {x} =\oint {\boldsymbol {\omega }}\times \mathbf {x} \cdot d\mathbf {x} =\oint {\boldsymbol {\omega }}\cdot \mathbf {x} \times d\mathbf {x} =2\oint {\boldsymbol {\omega }}\cdot d\mathbf {A} =2{\boldsymbol {\omega }}\cdot \mathbf {A}$$This gives Sagnac formula for ring interferometers of arbitrary shape and geometry$$\Delta \phi \approx {\frac {8\pi }{\lambda c}}{\boldsymbol {\omega }}\cdot \mathbf {A}$$If one also allows for stretching one recovers the Fizeau interference formula .

Since emitter and detector are traveling at the same speeds, Doppler effects cancel out, so the Sagnac effect does not involve the Doppler effect. In the case of ring laser interferometry, it is important to be aware of this. When the ring laser setup is rotating, the counterpropagating beams undergo frequency shifts in opposite directions. This frequency shift is not a Doppler shift, but is rather an optical cavity resonance effect, as explained below in Ring lasers.

The Sagnac effect has stimulated a century long debate on its meaning and interpretation, much of this debate being surprising since the effect is perfectly well understood in the context of special relativity

Other generalizations

A relay of pulses that circumnavigates the Earth, verifying precise synchronization, is also recognized as a case requiring correction for the Sagnac effect. In 1984 a verification was set up that involved three ground stations and several GPS satellites, with relays of signals both going eastward and westward around the world. In the case of a Sagnac interferometer a measure of difference in arrival time is obtained by producing interference fringes, and observing the fringe shift. In the case of a relay of pulses around the world the difference in arrival time is obtained directly from the actual arrival time of the pulses. In both cases the mechanism of the difference in arrival time is the same: the Sagnac effect.

The Hafele–Keating experiment is also recognized as a counterpart to Sagnac effect physics. In the actual Hafele–Keating experiment the mode of transport (long-distance flights) gave rise to time dilation effects of its own, and calculations were needed to separate the various contributions. For the (theoretical) case of clocks that are transported so slowly that time dilation effects arising from the transport are negligible the amount of time difference between the clocks when they arrive back at the starting point will be equal to the time difference that is found for a relay of pulses that travels around the world: 207 nanoseconds.

Reference frames

The Sagnac effect is not an artifact of the choice of reference frame. It is independent of the choice of reference frame, as is shown by a calculation that invokes the metric tensor for an observer at the axis of rotation of the ring interferometer and rotating with it yielding the same outcome. If one starts with the Minkowski metric and does the coordinate conversions $x=r\cos \left(\theta +\omega t\right)$ and $y=r\sin \left(\theta +\omega t\right)$ (see Born coordinates), the line element of the resultant metric is

$ds^{2}=(c^{2}-r^{2}\omega ^{2})\,dt^{2}-dr^{2}-r^{2}\,d\theta ^{2}-dz^{2}-2r^{2}\omega \,dt\,d\theta$

where

• $t$ is proper time for the central observer,
• $r$ is distance from the center,
• $\theta$ is the angular distance along the ring from the direction the central observer is facing,
• $z$ is the direction perpendicular to the plane of the ring, and
• $\omega$ is the rate of rotation of the ring and the observer.

Under this metric, the speed of light tangent to the ring is $c\pm r\omega$ depending on whether the light is moving against or with the rotation of the ring. Note that only the case of $\omega =0$ is inertial. For $\omega \neq 0$ this frame of reference is non-inertial, which is why the speed of light at positions distant from the observer (at $r=0$) can vary from $c$.