User:AhmedFrance123/sandbox

In geometry, a point $P'$ in the plane is called origami constructible if and only if, given a line segment $OP$ joining two points $O$ and $P$ in the plane, a line segment $OP'$ can be constructed using the origami axioms in a finite number of steps.

In algebra, a real number r is an origami-number if and only if there is a closed-form expression for r using only the integers 0 and 1 and the operations for addition, subtraction, multiplication, division, square roots and cube roots. The set of origami numbers forms a field: applying any of the four basic arithmetic operations to members of this set produces another origami number. This field is a field extension of the rational numbers and in turn is contained in the field of algebraic numbers. It is the smallest field extension of the rational numbers, that includes the square roots of all of its positive numbers and cube roots of all numbers.

The proof of the equivalence between the algebraic and geometric definitions has the effect of transforming geometric questions about 'paper folding' into algebra by introducing Cartesian coordinates in the plane. We say that a point $(a,b)$ is an origami constructible point if and only if $|a|$ and $|b|$ are origami numbers.

Note: In this article the terms constructible point and constructible number might be used interchangeably in which case the context can clarify what is being said.

Introduction

Modern origami constructions, from a mathematical perspective, are an attempt to construct segments of different lengths using certain geometric axioms. However, this attempt at construction of lengths using some geometric operations is hardly a new thing. Since ancient times humans have been interested in constructing different lengths using limited tools for practical reasons. The greeks pondered hard on straight edge and compass constructions. They came up with sophisticated techniques to construct different lengths. However, questions like doubling the cube, squaring the circle and trisecting an angle puzzled them and defied every line of attack. These questions were resolved only after the advent of modern mathematical tools from disciplines like abstract algebra and analytic geometry. This article is an attempt at applying these mathematical tools to exactly ascertain which lengths can be constructed using origami axioms (i.e. the set $\mathbb {O}$).

To paraphrase what the mathematician G. H. Hardy said , we can say that there are at least three distinct perspectives with which a point in an Euclidean plane can be viewed:

1. Geometric Perspective: A point can be viewed as a purely geometric entity.
2. Analytic Perspective: A point can be viewed as a vector emanating from a special fixed point (i.e. as an ordered pair of real numbers).
3. Algebraic Perspective: A point can be viewed as a complex number.

One of the axioms of higher mathematics that is often overlooked is that; there is a one-to-one correspondence between the set of ordered pairs of Real Numbers (and therefore the set of Complex numbers) and the Euclidean plane i.e. for every point in the plane there is a pair of real numbers (or a complex number) and that for every pair of real numbers (or a complex number) there is a point on the plane. This correspondence is the standard Cartesian co-ordinate system (or equivalently Complex number system).These correspondences establish the equivalence of these three perspectives. This axiom is one of the most brilliant strokes of human imagination because it helps us create analytical (or algebraic) representation of geometric entities and vice-versa. We will be using this axiom to convert the geometric axioms into algebraic operations in order to decipher the structure of the set of lengths that are constructible using origami axioms.

Geometric Perspective

Axioms for Geometric Construction

In origami constructions, we start with the Euclidean plane on which two points say $O$ and $P$ are initially given. An origami construction involves a sequence of single-fold operations as described by the Huzita–Hatori axioms which for the sake of completion are stated below.

Note: A single fold refers to the folding of paper once. A new fold can only be made after the paper is unfolded. Each fold leaves a crease that acts like an origami constructed line. Origami constructed points are the intersection points of these lines that can be constructed by using the following axioms finitely many times.

Axiom O1

Given two distinct points $P_{1}$ and $P_{2}$, we can fold a line $f$ that connects them.

Figure 1: Axiom O1

Axiom O2

Given two distinct points $P_{1}$ and $P_{2}$, we can create a line $f$ that folds $P_{1}$ onto $P_{2}$.

(One can clearly see that this fold will be perpendicular bisector of the segment joining $P_{1}$ and $P_{2}$.)   

Figure 2: Axiom O2

Axiom O3

Given two lines $l_{1}$ and $l_{2}$ , we can create a line $f$ that folds $l_{1}$ onto $l_{2}$.

(One can clearly see that this fold will be angle bisector of the lines $l_{1}$ and $l_{2}$.)

Figure 3: Axiom O3

Axiom O4

Given a line $l$ and a point $P$, we can fold a line $f$ passing through $p$ and perpendicular to $l$.

Figure 4: Axiom O4

Axiom O5

Given two points $P_{1}$ and $P_{2}$ and line $l$ we can create a line $f$ passing through $P_{1}$ that folds $P_{1}$ onto $l$.

(One can clearly see that this fold is equivalent to finding the intersection of a circle centred on $p_{2}$ and of radius that is length of segment joining $P_{1}$ and $P_{2}$ with the line $l_{1}$.)

Figure 5: Axiom O5

Axiom O6

Given two points $P_{1}$ and $P_{2}$ and two lines $l_{1}$ and $l_{2}$ we can create a line that folds $P_{1}$ and $P_{2}$ onto $l_{1}$ and $l_{2}$ respectively.

Figure 6: Axiom O6

Axiom O7

Given a point $P$ and two lines $l_{1}$ and $l_{2}$, we can create a line $f$ perpendicular to $l_{2}$ that folds $P$ onto $l_{1}$.       

Figure 7: Axiom O7

A note on the Axioms

According to Robert J. Lang, the first six axioms were first formulated by Humiaki Huzita in 1989 while the seventh axiom was found by Koshiro Hatori in 2003.

It is worth noting that these axioms are not independent. It has been shown that the operations O1 to O5 can be done by only using O6. Moreover, O7 also is dependent on the first 6 axioms. In reality, from a purely logical perspective only O6 really matters however, for practical reasons these other axioms are included.

Using combinatorial techniques the mathematicians Roger C. Alperin and Robert J. Lang in their paper showed that the axioms are complete. That is, the 7 operations described by the axioms, can be used to construct all possible alignments of lines and points in origami. Therefore, there is no need of another single-fold axiom.

Being familiar with the geometric axioms, we can now try to look at these axioms from an algebraic perspective.

Algebraic Perspective

Set of Origami Numbers forms a Field

If a and b are the non-zero lengths of origami-constructed segments then the axioms O1 to O6 can be used to obtain constructed segments of lengths a + b, a − b (if a ≥ b), ab and ⁠a/b⁠.

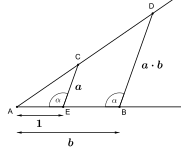
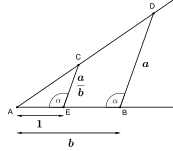
Closure under multiplication and division can be shown by using a construction based on the intercept theorem.

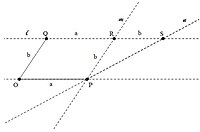
To show closure under addition and subtraction it suffices to only show closure under addition. Given two segments OP and OQ with corresponding lengths a and b fold a line 'm' parallel to OQ passing through P by applying O4 twice. Similarly, fold a line ' l ' parallel to OP passing through Q. Lengths of the segments QR and RP are a and b respectively because OPQR is a parallelogram. Now, by applying O3 we can construct a line 'n' by folding the line OP on the line 'm'. Let the point S be the intersection of 'l' and 'n'. Since 'n' is an angle bisector between 'm' and OP and since 'l' is parallel to OP, we know that the triangle RPS is isosceles and thus length of RS is b. Hence we have constructed a line segment QS with length a + b.

• Origami Constructions showing closure under field operations
• 
  $a\cdot b$ based on the intercept theorem
• 
  ${\frac {a}{b}}$ based on the intercept theorem
• 
  Constructing $a+b$ using axioms O3 and O4.

Therefore we have shown that the set of origami numbers $\mathbb {O}$, is closed under the four basic field operations and hence is a field (the remaining field axioms will obviously be satisfied).

Moreover, it is clear that the field of origami numbers $\mathbb {O}$ contains all rational numbers. Therefore, the field $\mathbb {O}$ is a field extension of $\mathbb {Q}$

"Algebraising" the geometric axioms

We have proved in the previous section that the set of origami numbers $\mathbb {O}$ is a field extension of the field of rational numbers $\mathbb {Q}$. Therefore, the operations corresponding to the origami axioms lead to field extensions of $\mathbb {Q}$. In this section we will use the analytic perspective described in the introduction to convert the geometric origami axioms into algebraic ones. In doing so, we wish to see which type of origami numbers are added into a given field $\mathbb {F}$ due to each of the axioms. This will help us determine exactly what kind of field extension of a given field $\mathbb {F}$ takes place (if any) due each axiom. Once we know this, we will be able to know in what way is the field of rationals i.e. $\mathbb {Q}$ is extended to yield the field of origami numbers $\mathbb {O}$.

(Note: The techniques from analytic geometry used below are standard ones and can be found in books like the book on coordinate geometry] by S. L. Loney .)

Now, each of the seven axioms constructs either a new line or a new point. Every time a new point is constructed its coordinates would be origami numbers. If a new line is constructed then coordinates of every point on the line, that are found by putting in numbers belonging in $\mathbb {F}$ for one of the variables in the equation of the line, will be constructible.

Now we are prepared for the following analysis:

Conversion of axiom O1

If two points $P_{1}\equiv (x_{1},y_{1})$ and $P_{2}\equiv (x_{2},y_{2})$ are given then the fold line connecting them is $f\equiv (y-y_{1})={\frac {(y_{2}-y_{1})}{(x_{2}-x_{1})}}(x-x_{1})$.

Clearly, if we put into the equation of the line $f$ either value of $x$ or the value of $y$ from a field $\mathbb {F}$, the corresponding value of the other variable would still lie in $\mathbb {F}$ because of closure of a field over four basic arithmetic operations. Hence, axiom O1 adds no new point in the field $\mathbb {F}$.

Conversion of axiom O2

If two points $P_{1}\equiv (x_{1},y_{1})$ and $P_{2}\equiv (x_{2},y_{2})$ are given then the fold line mapping one onto the other is $f\equiv (y-{\frac {y_{1}+y_{2}}{2}})=-{\frac {(x_{2}-x_{1})}{(y_{2}-y_{1})}}(x-{\frac {x_{1}+x_{2}}{2}})$. As said earlier this is the equation of perpendicular bisector of the segment $P_{1}P_{2}$.

For the same reasoning as axiom O1, axiom O2 does not add any new point to the field $\mathbb {F}$.

Conversion of axiom O3

To convert axiom O3 into algebra, we can assume without loss of generality that the two lines given are $l_{1}\equiv y+1=0$ and $l_{2}\equiv mx-y+c=0$. Then the equations of the two angle bisectors of these would be as follows: $f\equiv {\frac {mx-y+c}{\sqrt {m^{2}+1}}}=\pm (y+1)\implies f\equiv x={\frac {(1\pm {\sqrt {m^{2}+1}})(y+1)-c-1}{m}}$.

We know that according to our assumptions $m\in \mathbb {F}$. Now, if we put into the equation of the line $f$ either value of $x$ or the value of $y$ from a field $\mathbb {F}$, the corresponding value of the other variable might not lie in $\mathbb {F}$ because $\mathbb {F}$ might not be closed under the operation of taking square-roots. Therefore, axiom 3 might lead to a an extension of the field $\mathbb {F}$. For example, if $y=0=c$ and $m=1$ then $x=\pm {\sqrt {2}}$. Now, if $\pm {\sqrt {2}}$ does not belong in $\mathbb {F}$ then clearly axiom O3 can lead to the field extension $\mathbb {F} ({\sqrt {2}})$

Conversion of axiom O4

If a point $P\equiv (x_{1},y_{1})$ and a line $l\equiv mx-y+c=0$ are given then the fold line perpendicular to $l$ and passing through $P$ is given by $f\equiv x+my-x_{1}-my_{1}=0$

We know that according to our assumptions $m\in \mathbb {F}$. Therefore, for the same reasoning as axiom O1, axiom O4 does not add any new point to the field $\mathbb {F}$.

Conversion of axiom O5

To convert axiom O5 into algebra, we can say without loss of generality that, the line $l\equiv y+1=0$ and the two points $P_{1}\equiv (0,1)$ and $P_{2}\equiv (x_{2},y_{2})$ are given. Then the fold line $f$, passing through $P_{2}$ that maps $P_{1}$ onto $l$ is derived below:

Let, $P_{1}'\equiv (t,-1)$ be the point on which $P_{1}$ maps after the fold operation. It is then obvious by using O2 that the fold line $f$ would be the perpendicular bisector of the segment $P_{1}P_{1}'$. Hence, $f\equiv y-{\frac {1+(-1)}{2}}=-{\frac {0-t}{1-(-1)}}(x-{\frac {0+t}{2}})\implies f\equiv y={\frac {t}{2}}(x-{\frac {t}{2}})$.

Now, we know that $f$ passes through (x_2, y_2) therefore $y_{2}={\frac {t}{2}}(x_{2}-{\frac {t}{2}})\implies t^{2}-2x_{2}t+4y_{2}=0$.

Clearly, axiom O5 leads to the construction of a point, the $x$-coordinate of which (i.e. $t$) is the root of a general quadratic equation, the coefficients of which lie in $\mathbb {F}$. It is therefore clear that axiom O5 can lead to any field extension of $\mathbb {F}$ of degree at most 2.

Conversion of axiom O6

To convert axiom O6 into algebra, we can say without loss of generality that, the two lines $l_{1}\equiv y+1=0$ and $l_{2}\equiv mx-y+c=0$ and the two points $P_{1}\equiv (0,1)$ and $P_{2}\equiv (x_{2},y_{2})$ are given. Then the fold line $f$, that would map $P_{1}$ and $P_{2}$ on $l_{1}$ and $l_{2}$ respectively would be as described below:

Let, $P_{1}'\equiv (k,-1)$ and $P_{2}'\equiv (t,mt+c)$ be the points on whom the points $P_{1}$ and $P_{2}$ respectively map after the fold operation. It is then obvious by using O2 that the fold line $f$ would be the perpendicular bisector of both segments $P_{1}P_{1}'$ and $P_{2}P_{2}'$ simultaneously.

Hence, $f\equiv y-{\frac {1+(-1)}{2}}=-{\frac {0-k}{1-(-1)}}(x-{\frac {0+k}{2}})\implies f\equiv y={\frac {k}{2}}(x-{\frac {k}{2}})$ (Note: This equation is 'representation 1 of $f$ ')

and

$f\equiv y-{\frac {(mt+c)+(y_{2})}{2}}=-{\frac {(x_{2}-t)}{[y_{2}-(mt+c)]}}(x-{\frac {x_{1}+x_{2}}{2}})$ (Note: This equation is 'representation 2 of $f$ ')

We can equate the slopes of the two equations of lines stated above because they represent the same fold $f$. On doing so we get the equation:

${\frac {k}{2}}=-{\frac {(x_{2}-t)}{[y_{2}-(mt+c)]}}$. (Note: This is 'Equation 1')

Moreover, we know that the mid point of the segment $P_{2}P_{2}'$ passes through $f$. Therefore, we can evaluate the 'representation 1 of $f$' at the coordinates of this point to get the equation:

${\frac {(mt+c)+y_{2}}{2}}={\frac {k}{2}}({\frac {x_{1}+t}{2}}-{\frac {k}{2}})$. ((Note: This is 'Equation 2'))

It is clear that if one uses the equations 1 and 2 stated above to eliminate the variable $k$ one would end up with a complicated cubic polynomial equation in $t$ of the form: $At^{3}+Bt^{2}+Ct^{3}+D=0$.

Clearly, axiom O6 leads to the construction of a point, the $x$-coordinate of which (i.e. $t$) is the root of a general cubic equation, the coefficients of which lie in $\mathbb {F}$. It is therefore clear that axiom O6 can lead to any field extension of $\mathbb {F}$ of degree at most 3.

Conversion of axiom O7

To convert axiom O7 into algebra, we can say without loss of generality that, the two lines $l_{1}\equiv y+1=0$ and $l_{2}\equiv mx-y+c=0$ and the point $P\equiv (0,1)$ are given. The fold line $f$ that maps $P$ onto a point $P'\equiv (t,-1)$ lying on the line $l_{1}$ is given by: $f\equiv y={\frac {t}{2}}(x-{\frac {t}{2}})$. Now this fold line is perpendicular to $l_{2}$. Therefore, the slope of $f$ will be $-{\frac {1}{m}}$. Hence, ${\frac {t}{2}}=-{\frac {1}{m}}\implies t=-{\frac {2}{m}}$.

We know that according to our assumptions $m\in \mathbb {F}$ which means that $t\in \mathbb {F}$. Hence, axiom O7 does not add any new numbers to $\mathbb {F}$.

Conclusions drawn from the transformation

Interpretation of the conversion of axioms

Using the analysis of the previous section it can be seen clearly that the operations of axioms O1, O2, O4 and O7 do not add any new points to a given field $\mathbb {F}$. It can be seen that axiom O5 can lead to a field extension if the field $\mathbb {F}$ does not contain ${\sqrt {m^{2}+1}}$. Axiom O5 can lead to at most a two degree extension of the field $\mathbb {F}$ and hence any field extension possible due to axiom O3 is also possible due to axiom O5. Finally, the axiom O6 can lead to at most a three degree extension of the field $\mathbb {F}$ and therefore this axiom, from a logical perspective, is equivalent to all other axioms combined.

We know that the field of origami numbers contains the field of rational numbers $\mathbb {Q}$. This means that any origami number lies in some field extension of $\mathbb {Q}$ that is formed by using axioms O1 to O7 in some order, finitely many times. This fact gives us a way to define an origami number in a purely algebraic way. A real number $x$ is an origami number if and only if the smallest field extension of $\mathbb {Q}$ containing $x$ i.e. the field $\mathbb {Q(x)}$ has a degree of the form $2^{a}3^{b}$ where $a,b\in \mathbb {N}$ (this is because axioms either do not lead to an extension or they lead to an extension of degree 2 or 3).

In the notation of field extensions we write this as: $x\in \mathbb {O} \iff [\mathbb {Q(x):Q} ]=2^{a}3^{b}$ where $a,b\in \mathbb {N}$.

Relationship with constructible numbers ($\mathbb {K}$)

In the previous section we saw how we can define origami numbers as numbers that lie in field extensions of $\mathbb {Q}$ with degree of extension being of the form $2^{a}3^{b}$. If one were to read the wiki page of constructible numbers, they will see that if a similar algebraic analysis as we have done on origami constructions, were done on straight-edge and compass constructions, then the constructible numbers can be defined as real numbers such that smallest field extension of $\mathbb {Q}$ containing them has a degree of the form $2^{a}$.

In mathematical notation this means that: $x\in \mathbb {K} \iff [\mathbb {Q(x):Q} ]=2^{a},a\in \mathbb {N}$.

It therefore becomes clear that: $\mathbb {K} \subset \mathbb {O}$. This conclusion could have been reached intuitively before our rigorous analysis by observing that origami axiom O5 is effectively equivalent to finding intersection of a line and a circle which is what happens in a ruler and compass construction!

${\displaystyle }$