User:حلیم وردګ
د پښتو ژباړې لپاره را وړل شوی د انجینري جوړښتونو د شننې یوه لاره () ده چې په () سره هم یادیږي. دا لاره زیاتره د کمپیوټر پر مرسته ولاړې شننې لپاره کارول کیږي. ځکه پدې لاره یا رویښ کې پیچلې زیاضیکي او فزیکي معادلې کارول کیږي چې د هغو حل په ګوتو ډیر ستونزمن او د زیات وخت غوښتونکی دی. دا رویښ د نا معین-سټاټیکي او همدا راز پیچلو جوړښتونو د شننې لپاره هم یوه غوره وسیله بللی شو. پدې رویښ کې د یو جوړښت د هر غړي () د سختوالي () څخه د یاد غړي د داخلي قوې او بیځایښت () د موندلو په موخه کار اخیستل کیږي. دا () رویښ د فاینیټ ایلیمنټ رویښ تر ټولو معمول او زیات کاریدونکی رویښ دی. پدې رویښ کې یو جوړښت یا سیستم په وړو، وړو داسې ټوټو ویشل کیږي چې له یو بل سره په غوټو () کې تړل شوي وي. دې دغو وړو ټوټو د جوړونکو موادو سختي بیا د مترکسونو د ریاضي په مرسته په یو مترکس اړول کیږي. لاسته راغلی مترکس بیا د ټول سیستم د رفتار څرګندويي کوي. پدې توګه د یو جوړښت یا سیستم ټول ناڅرګنده () بیځایښت او داخلي قوې تر لاسه کیدی شي. د زیاتره سوداګریزو پوستکالو () بنسټ پر همدې رویښ ولاړ دی. دا رویښ په لمړي ځل په الوتک جوړونه () کې را وټوکید. څیړونکو د بیلابیلو لارو او رویښونو له مخې د الوتکو فرمونه وکتل. لکه د ارتجاعیت نظریه، د انرژۍ اصول د جوړښتونو په میخانیک کې، د نرمښت رویښ او د مترکس رویښ. ددې رویښونو د شننې او کتنې وروسته د ډایرکټ سټیفنیس میتود د کمپیوټري پروګرام جوړونې لپاره تر ټولو غوره را ووت. تاریخچه د 1934 او 1938 کلونو ترمنځ () او () د
As one of the methods of structural analysis, the direct stiffness method, also known as the matrix stiffness method, is particularly suited for computer-automated analysis of complex structures including the statically indeterminate type. It is a matrix method that makes use of the members' stiffness relations for computing member forces and displacements in structures. The direct stiffness method is the most common implementation of the finite element method (FEM). In applying the method, the system must be modeled as a set of simpler, idealized elements interconnected at the nodes. The material stiffness properties of these elements are then, through matrix mathematics, compiled into a single matrix equation which governs the behaviour of the entire idealized structure. The structure’s unknown displacements and forces can then be determined by solving this equation. The direct stiffness method forms the basis for most commercial and free source finite element software.
The direct stiffness method originated in the field of aerospace. Researchers looked at various approaches for analysis of complex airplane frames. These included elasticity theory, energy principles in structural mechanics, flexibility method and matrix stiffness method. It was through analysis of these methods that the direct stiffness method emerged as an efficient method ideally suited for computer implementation.
History
[edit]Between 1934 and 1938 A. R. Collar and W. J. Duncan published the first papers with the representation and terminology for matrix systems that are used today. Aeroelastic research continued through World War II but publication restrictions from 1938 to 1947 make this work difficult to trace. The second major breakthrough in matrix structural analysis occurred through 1954 and 1955 when professor John H. Argyris systemized the concept of assembling elemental components of a structure into a system of equations. Finally, on Nov. 6 1959, M. J. Turner, head of Boeing’s Structural Dynamics Unit, published a paper outlining the direct stiffness method as an efficient model for computer implementation (Felippa 2001).
Member stiffness relations
[edit]A typical member stiffness relation has the following general form:
where
- m = member number m.
- = vector of member's characteristic forces, which are unknown internal forces.
- = member stiffness matrix which characterises the member's resistance against deformations.
- = vector of member's characteristic displacements or deformations.
- = vector of member's characteristic forces caused by external effects (such as known forces and temperature changes) applied to the member while ).
If are member deformations rather than absolute displacements, then are independent member forces, and in such case (1) can be inverted to yield the so-called member flexibility matrix, which is used in the flexibility method.
System stiffness relation
[edit]- See also: Stiffness matrix
For a system with many members interconnected at points called nodes, the members' stiffness relations such as Eq.(1) can be integrated by making use of the following observations:
- The member deformations can be expressed in terms of system nodal displacements r in order to ensure compatibility between members. This implies that r will be the primary unknowns.
- The member forces help to the keep the nodes in equilibrium under the nodal forces R. This implies that the right-hand-side of (1) will be integrated into the right-hand-side of the following nodal equilibrium equations for the entire system:
where
- = vector of nodal forces, representing external forces applied to the system's nodes.
- = system stiffness matrix, which is established by assembling the members' stiffness matrices .
- = vector of system's nodal displacements that can define all possible deformed configurations of the system subject to arbitrary nodal forces R.
- = vector of equivalent nodal forces, representing all external effects other than the nodal forces which are already included in the preceding nodal force vector R. This vector is established by assembling the members' .
Solution
[edit]The system stiffness matrix K is square since the vectors R and r have the same size. In addition, it is symmetric because is symmetric. Once the supports' constraints are accounted for in (2), the nodal displacements are found by solving the system of linear equations (2), symbolically:
Subsequently, the members' characteristic forces may be found from Eq.(1) where can be found from r by compatibility consideration.
The direct stiffness method
[edit]It is common to have Eq.(1) in a form where and are, respectively, the member-end displacements and forces matching in direction with r and R. In such case, and can be obtained by direct summation of the members' matrices and . The method is then known as the direct stiffness method.
The advantages and disadvantages of the matrix stiffness method are compared and discussed in the flexibility method article.
Example
[edit]Breakdown
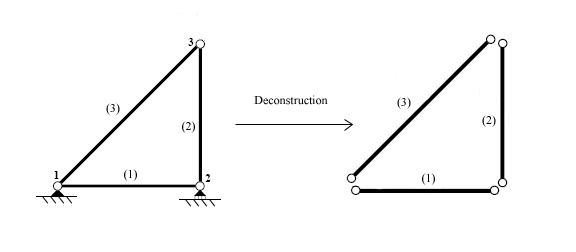
[edit]The first step when using the direct stiffness method is to identify the individual elements which make up the structure.
Once the elements are identified, the structure is disconnected at the nodes, the points which connect the different elements together.
Each element is then analyzed individually to develop member stiffness equations. The forces and displacements are related through the element stiffness matrix which depends on the geometry and properties of the element.
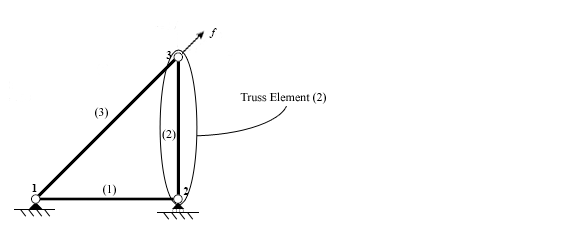
A truss element can only transmit forces in compression or tension. This means that in two dimensions, each node has two degrees of freedom (DOF): horizontal and vertical displacement. The resulting equation contains a four by four stiffness matrix.
A frame element is able to withstand bending moments in addition to compression and tension. This results in three degrees of freedom: horizontal displacement, vertical displacement and in-plane rotation. The stiffness matrix in this case is six by six.
Other elements such as plates and shells can also be incorporated into the direct stiffness method and similar equations must be developed.
Assembly
[edit]Once the individual element stiffness relations have been developed they must be assembled into the original structure. The first step in this process is to convert the stiffness relations for the individual elements into a global system for the entire structure. In the case of a truss element, the global form of the stiffness method depends on the angle of the element with respect to the global coordinate system (This system is usually the traditional Cartesian coordinate system).
(for a truss element at angle β)
After developing the element stiffness matrix in the global coordinate system, they must be merged into a single “master” or “global” stiffness matrix. When merging these matrices together there are two rules that must be followed: compatibility of displacements and force equilibrium at each node. These rules are upheld by relating the element nodal displacements to the global nodal displacements.
The global displacement and force vectors each contain one entry for each degree of freedom in the structure. The element stiffness matrices are merged together by augmenting or expanding each matrix in conformation to the global displacement and load vectors.
(for element (1) of the above structure)
Finally, the global stiffness matrix is constructed by adding the individual expanded element matrices together.
Solution
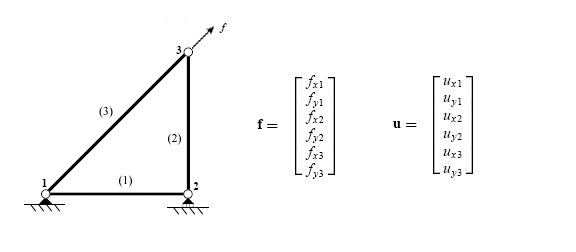
[edit]Once the global stiffness matrix, displacement vector and force vector have been constructed, the system can be expressed as a single matrix equation.
For each degree of freedom in the structure, either the displacement or the force is known.
After inserting the known value for each degree of freedom, the master stiffness equation is complete and ready to be evaluated. There are several different methods available for evaluating a matrix equation including but not limited to Cholesky decomposition and the brute force evaluation of systems of equations. If a structure isn’t properly restrained, the application of a force will cause it to move rigidly and additional support conditions must be added.
The method described in this section is meant as an overview of the direct stiffness method. Additional sources should be consulted for more details on the process as well as the assumptions about material properties inherent in the process.
Applications
[edit]The direct stiffness method was developed specifically to effectively and easily implement into computer software to evaluate complicated structures that contain a large number of elements. Today, nearly every finite element solver available is based on the direct stiffness method. While each program utilizes the same process, many have been streamlined to reduce computation time and reduce the required memory. In order to achieve this, shortcuts have been developed.
One of the largest areas to utilize the direct stiffness method is the field of structural analysis where this method has been incorporated into modeling software. The software allows users to model a structure and, after the user defines the material properties of the elements, the program automatically generates element and global stiffness relationships. When various loading conditions are applied the software evaluates the structure and generates the deflections for the user.
See also
[edit]- Finite element method
- Finite element method in structural mechanics
- Structural analysis
- Flexibility method
- List of finite element software packages
External links
[edit]- Application of direct stiffness method to a 1-D Spring System
- Matrix Structural Analysis
- Animations of Stiffness Analysis Simulations
References
[edit]- Felippa, Carlos A. (2001), "A historical outline of matrix structural analysis: a play in three acts" (PDF), Computers & Structures, 79 (14): 1313–1324, doi:10.1016/S0045-7949(01)00025-6, ISSN 0045-7949
- Felippa, Carlos A. Introduction to Finite Element Method. Fall 2001. University of Colorado. 18 Sept. 2005 <http://www.devdept.com/fem/books.php>
- Robinson, John. Structural Matrix Analysis for the Engineer. New York: John Wiley & Sons, 1966
- Rubinstein, Moshe F. Matrix Computer Analysis of Structures. New Jersey: Prentice-Hall, 1966
- McGuire, W., Gallagher, R. H., and Ziemian, R. D. Matrix Structural Analysis, 2nd Ed. New York: John Wiley & Sons, 2000.
Category:Structural analysis Category:Numerical differential equations
زلزله
زلزله هغه طبعيی افت دی چې د ځمکی د لړزش په واسطه منځ ته راځي. که په ژوند کې ېو وار چا زلزله ليدلی اوسي، نو هغه زلزلی ته په خاص احترام قاېليږي.
پخوا به د ايټالی او يونان عالمانو فکر کولو چې د ځمکی په مخ وچی په اوبو کې لکه د بېړۍ غوندی لمبيږي، څنګه چې بېړۍ په اوبو کې دېخوا هغه خوا ځنګيږی، همدا رنګه ځمکه هم چې ددی په وجه زلزلهمنځ ته راځي. بعضو به دا فکر کولو چې زلزله د سوړو او غارونو څخه منځ ته راځي. جاپانيانو فکر کولو چې زلزله هغه وخت منځ ته راځي، کله چې خامار (کوم چې دوی پری عقيده لري) په قهر شي نو د خولی څخه يی اور اوځي او ځمکه په لړزش راولي. د 20 قرن په شروع کې کله چې د الفريد واګنېر له خوا نه تيکتونيکی تختو نظريه وپېژندل شوه، د زلزلی د منځ ته راتلو علت باند سړی پوه شو.
د زلزلی ډولونه:
اساساً زلزله دوه ډولونه لري: ېو تېکتونيکي زلزله ده او بله يی ولکانيکي زلزله ده. خو کله کله داسی هم کيږي چې د زلزلی نه وروسته ځمکه وښويږي. بله دا چې د ځمکی لرزش د بعضی چاودنو په واسطه هم منځ ته راځي خصوصاً هغه ضروري ازماېښتونه چې د قدرتمندانو له خوانه کيږي. د ېوې عادي چاودنی مثال چې زما د سترګو ليدلی حال دی، هغه دا کله چې ما په کابل کې وظيفه درلوده، نو د هوايی ډګر شاته په غره کې خانه سازي د ساختماني ډبرو د پاره چاودنه وکړه چې ددغی چاودنې په وجه تر بي بي مهرو پوری ساحه ولړزېده.
زلزله څه ته وايي؟
زلزله هغه پروسه ده چې د ځمكې لاندې د لېتوسفېر په طبقه كې واقع كيږي.
زلزله هغه وخت منځ ته راځي كله چې د ډبرو لوېې كتلې په مداوم يا بې د دمې خپل حجم ته په ډېر قوت سره تغير وركړي او په ېو كمزوري سيمه كې په ناڅاپه ډول ېو چاود منځ ته راوړي چې د دغو ډبرو كتلې په دغه كمزوري سيمه كې په ېودم دواړو خواو ته په حركت راځي او د ځمكې لاندې د ېو لړزش علت گرځي. دا ډول پېښې د ځمكې په پورتنۍ طبقې او د ځمكې په دوهمې طبقې كې واقع كيږي ، كوم چې د ډبرو هغه تختې چې ېوبل سره نږدې واقع دي او تغيرد حجم پكې موجودې دي.
د زلزلې د تفاهم دپاره باېد سړئ پوه شي، چې ځمكه په منځ منځ كې كوم قوي جسم هم نه دئ. نظر په هغه نتيجو چې دزلزلې د څپو څخه لاس ته راغلي، سړئ پوهيږي چې ځمكه لكه د ېو پيازغوټې په شكل د مختلفو پوټكو څخه جوړه شوې ده، چې دا هر ېو ېې د كيمياوي، د موادو تغيرات، تودوخي (حرارت) او د گڼ والي په لحاظ د ېوبل نه ډېر تفاوت لري چې ددې جملې څخه ډېر مهم يې د ځمكې پورتنۍ طبقه، د ځمكې دريم قشر او د ځمكې مركزي قشر دې.
د ځمكې پورتنئ يا لومړنئ قشرد ځمكې د وچې قارې او اوقيانوس څخه تسكيل شوئ. د ځمكې وچه قاره د ۲۵ او ۵۰كيلو مترو پورې غښتلئ (ډبل) دئ چې زياته اندازه د كم تېزابي ډبرو لكه گرانيت څخه تشكيل شوېدې. د اوقيانوس برخه د هغه د لوېوالي سره سره بيا هم ډېر كم د ۵ او ۸ كيلو مترو په منځ كې غښتلئ دئ او په زياته اندازه د گڼ بازالت ډبرو څخه تشكيل شوېدې.
د ځمكې لمړنئ قشر او د ځمكې د دوهم قشر پورتنۍ برخه دواړه ېوه طبقه جوړوي چې د ليتوسفېر په نوم ياديږي. ليتو په يوناني كې د ډبرې مانا وركوي. ليتوسفېر كلك او ددي دپاره چې د ځمكې پورتنۍ برخې ته نږدې دئ نو ځكه تقريباً سوړ دئ. ددى طبقې غښتلوالئ (پېړوالئ) د ۷۰ او ۱۲۰ كيلو مترو په منځ كې دئ. د دغې طبقې لاندې بله طبقه ده چې د استېنوسفېر په نوم ياديږي. استېنو په يوناني كې د پوست (نرم) مانا وركوي چې دا طبقه شخه او د پلاستيك په شان عكس العمل لري او د ۱۰۰۰ نه تر ۱۲۰۰ درجى سانتيګريت پورې تودوخي (حرارت) لري. د ډبرو له ډېر زيات زور (فشار) په وجه چې د (۱۰ټنه/متر مربع) څخه زيات دئ او د ليتوسفېر په سر واقع دئ،بيا هم نه شي كولائ چې دا تودې ډبرې ويلې كړي، سره ددې چې تودوخي هم په كافي اندازه موجوده ده.
لاندينئ قسمت د ځمكې د دوهمې طبقې پورتنۍ برخه ميسوسفېر جوړوي چې ميسو په يوناني كې د منځ مانا لري چې دا د ځمكې په ۳۵۰ او ۷۰۰ كيلو مترو كې ښكته پروت دئ. د ۲۹۰۰ كيلو مترو په ژور والي كې د ځمكې د دوهمې طبقې لاندينۍ برخه ده.
د ځمكې منځنۍ (مركزي) طبقه د ۵۰۰۰ كيلو مترو په اندازه ټيټه پروته ده چې دا طبقه د زلزله سنج عالمانو د نتيجو څخه اوبلنه (مايع) او ډېره توده ده چې د تودوخي (حرارت) درجه ۶۰۰۰ سانتيگريت ته رسيږي او دا د اوسپنې او نكل څخه گډ (الياژ) دئ.
په ليتوسفېر كې ډېر زښت د ډبرو تختې ړنګيږي او يا تجزيه كيږي کوم چې دا بيا په ايستوسفېر كې چې د پلاستيك ډوله عكس العمل لري، گډيږي او تل په حركت كې وي. ددى دننئ زور دومره زيات وي چې سړئ فكر كوي دا د ځمكې په دريمه طبقه كې د برق ېوه سخته جرقه ده. ددى جريان لا عامل تر اوسه لا نا معلوم دئ. كله چې دغه د ډبرو تختې ېو بل سره ولگيږي، ېو بل څخه بېلې شي او يا د ېو بل د خوا څخه په سولېدو تېرې شي، نو دغه تختې بيا خپل حجم ته په ډېر قوت سره تغير وركوي او ېو سخت تشنج منځ ته راوړي چې ورڅخه زلزله جوړيږي.
د زلزلی ساحی :
د زلزلی ساحی دتېکتونيکي لوېو تختو ساحی دي، چی هغه عبارت دي له:
د ارام اوقيانوس او انترکتيکا تختته، شمالي او جنوبي امريکی تخته، افريقايی او اوروپايی تخته او د استراليا تخته.
ددی په خوا کې نوری وړی تختې هم شته چې عبارت دي له:
کاريبيک تخته، کوکوس تخته، کوکس (منځنی امريکا) تخته، نازکا تخته، هندي تخته، سکوتيا تخته، عرب تخته او د فليپين تخته.
د زلزلې پېښه:
د زلزلې پېښېدل د عالمانو په نظر دا د ځمكې شكېدلو يا چاودېدلو فرضيه ده چې دغه تيوري تر ننه پورې هم د اعتبار وړ ده. دغه د ځمكې شكېدل يا چاودېدل په ليتوسفېر كې د هغو تختو تر منځ پولې (سرحدونه) دي، چې دا په عمودي زاويو ېو پر بل سړكونه او لارې جوړوي او بيا دغه تختې په ډېر ېو قوي حركت سره هغه ځاېو ته كوم چې مزاهمت يا ورانئ پكې راغلئ، متقابل پورې وهل كيږي. هغه كومې تختې چې په مزاهمت ځائ كې واقع دي، ددې د پاره چې د پورې وهل شوو تختو مخنيوئ وكړي او يا د ېو بل څخه تېرې شي، برعكس دغه تختې په دغه مزاهم ځائ كې خپلو څنډو ته تغير د شكل وركوي، هغه مستقيم سړكونه او لارې چې وې، خپل شكل بدلوي او په كگلېچو بدليږي بيا دا پورې وهل ودريږي او په متداوم ډول سره د څنډو د تغيرشكل په وجه ېو تشنج منځ ته راځي چې سړئ ورته بېاطي (قېچي) كوونكئ تشنج وېلئ شي. دا كېدئ شي چې تر لسونو كلونو پورې دوام وكړي، ېو نه ېو وخت دا تشنج دومره لويږي چې د مزاهمت په ځائ كې د ماتېدو په وجه سولېدنه شروع كړي او په دې ځائ كې بيا د دغه تختو څنډې ېو ناڅاپه په پورې وهلو شروع وكړي چې د پورته الوتنو اندازه يې دومره زياته وي چې مترونو فاصلو سره ډېره ساحه لاندې كوي. په دغه مزاهم ځائ كې بېرته ېوه ټېله (لكه د ربړ په شان چې راښكل شي او بېرته خپل ځاى ته راشي) منځ ته راځي چې دلته هغه ډبرې چې خپل شكلونو ته تغير وركړئ وو، ډېر په سرعت سره ېو كمزره تشنجي حالت غوره كوي. هغه سړكونه او لارئ چې كگلېچې وې، بېرته خپل حالت نيسي خو خپل ځاېو ته تغير وركوي. د دغه ازاده پاتې شوې اينرژي ېوه برخه په تودو وړانگو د زلزلې په څپو د ټولې ځمكې پر مخ منځ ته راځي او زلزلهورڅخه جوړيږي. د مزاهمت په هغه ځائ كې چې د ډبرو تختې ېو ناڅاپه خپل پورې وهنه شروع كوي، دا ټكى (نقطه) د زلزلى د داش يا د ځمكې په دننه كې د زلزلې اصلي مركز په نوم ياديږي او عمودي دده په سرد ځمكې په پورتنۍ سطح واقع ټكئ (نقطى) ته د ځمكې په سر د زلزلې مركز وېل كيږي. كله كله د ډبرو دغه كتلې په عمودي ډول پورې وهنه هم كوي چې ددې په وجه د ځمكې پر مخ لكه د پوړۍ( زينې) په شان چاود منځ ته راځي. څومره چې دغه پوري وهنه قوي او پراخه وي، هومره انرژي ازادوي او همدا رنگه زلزله قوي وي. په لوېو زلزلو كې د ځمكې د چاود اندازه په مترونو ژور او په كيلومترونو اوږود وي.
د زلزلې نه مخكې زلزله او د زلزلې نه وروسته زلزله:
د ېوې زلزلې سره مخكې او وروسته زلزله مل وي. د زلزلې څخه مخكې(مقدماتي)زلزله دهغو ډبرو تغير د شكل څخه منځ ته راځي، چې دا ډبرې په مزاهم ځائ كې په پورې وهنه شروع وكړي. ددې د پاره چې دلته فيزيكي شرايط لا قوي پورې وهنى ته برابر نه دي، نو ځكه وړاندې نه ځي خو بيا هم دى مقدماتي زلزلې سره ډېر واړه درزونه منځ ته راځي چې دا بيا په مرور د وخت سره خپل تشنج ذخيره كوي او په ېو قوي پورې وهنه شروع كوي چې غټ درځونه او چاود منځ ته راځي چې د قوي زلزلى علت كيږي.
د زلزلې زياتره واقعات او قوت:
ډېرو خلكو ته ځمكه ېوه ټينگه، تغير نه خوړنكې او حتى ېو نيم ته د بقاً ېو سمبول دې. دوۍ باور لري چې په ټينگه ځمكه قدم وهي، خو دا ېوه غولېدنه ده. د ځمكې لاندې په هيڅ ځائ كې ارام نه شته. زلزله سنج ښودلې ده چې په ټوله دنيا كې هر كال د ۸۰۰۰۰۰ څخه زيات د ځمكې لاندې لړزشونه منځ ته راځي چې دغه سړئ ډېر كم او يا هيڅ احساسولئ نه شي. په كال كې ۱۰۰ زلزلې د ۶ او ۷ درجو پورې واقع كيږي. د ۵ او ۱۰ كلونو منځ كې په ېو ځائ كې چې د زلزلې ساحه وي، د ۸درجو څخه قوي زلزله منځ ته راځي.
سره ددې چې زلزله ډېر تاوانونه او خرابي منځ ته راوړي، خو بيا هم خلك د زلزلې كېدل د نصيب او قسمت پورى تړي.
ډېرې قوي زلزلې زياتره په جاپان كې واقع كيږي. د هغه وخت نه چې د زلزلې قوت ښودونكئ د ۱۹۰۴ نه شروع شوېدئ، تر اوسه قوي ترينه زلزله په ۲ د مارچ ۱۹۳۳ د جاپان په ختيځ ساحل كې د ۸،۹ درجو په اندازه وه. نورې زلزلې په ۱۹۶۴ الاسكا كې د ۸،۴ درجو په اندازه او د مكسيكو په ښار كې ۱۹۸۵ د ۸،۱ درجو په اندازه وې. د ټولو نه قوي زلزله چې په ۱۷۵۵ كې په ليسابون كې واقع شوې وه، د ۹ درجو په اندازه اټكل شوئ وو.
ولکاني زلزله :
د ولکان کليمه د ايټالی د ولکانو جزيری څخه اخستل شوی دی.
دننه په ځمکه د 100 km په ژوره کی د 1000 - 1500º پوری ډبری ويلي کيږي، چې دغه ويلی شوي ډبری د څاسکو په ډول د 2 – 50 km پوری ښکته تويږي او هلته سره ټوليږي، کله چې فشار زيات شي، نو دا بيا د ليتوسفېر په طبقه کې د درزونو او چاود له لاری پورته کيږي او بيا د د ځمکی پر مخ بهيږي چې دی ته لاوا وېل کيږي.
د ولکاني زلزلو ساحی :
د نړۍ په مخ تقريباً 1500 فعاله ولکانونه شته چې دا په هر براعظم کې موجود دي خو دا په مساوي ډول نه دي تقسيم شوي بلکه دا په هر ځای کې په خاص ډول برسېره کيږي. چې ددی جملی څخه د ارام اوقيانوس د اور کړۍ ده چې دا د غټترينه ځنځيري کړۍ د ولکان ده. دا د نيوزلېند څخه شروع کيږي او امتداد پېداکوي ايندونيزيا ته، بيا د فليپين او جاپان څخه تېريږي د روسی نيمی وچی کامچاتکا څخه تر الاسکا پوری. بيا د د کاناډا، مرکزي او جنوبي امريکی نه او په اخره کې په کلېفورنيا کې ختميږي.
مشهوری اور غورځونکی غرونه عبارت دي له:
ويزېو او اتنا په ايټاليا کې، د هېلېن غرونه په امريکی کې، په فليپين کې پيناتوبو، اېرا د جاپان په کيوشو کی، اسو هم د جاپان په کيوشو کې، کيکاې د جاپان په ريوکيو کې، لاکېتوبا په ايندونيزيا کې، لونګ وېلي چېلدېرا د امريکی په کلېفورنيا کې، ټاوپو زی په نيوزلېند کې او وېلي ګرېند په مکسيکو کې.
د زلزلې تاوانونه:
زلزله په راز راز ډولونو ورانئ لري. د زلزلې اغيزه د هغه د قوت او د مركز (ايپوسنتر) څخه د لېرې والي پورې اړه لري.كه د زلزلې ټكان د زلزلې مركز ته نږدې او يا د زلزلې د داش په سر وي، دومره قوي وي، چې هغه شيان كوم چې په دغه ځائ كې وجود ولري، نو هوا ته يې الوزوي، ودانۍ په ټكان لړزوي چې يا خو نړيږي او يا چپه كيږي . د زلزلې څپې غېر ددنه نورې جانبي اغيزې هم لري. كله چې د اوبو رسولو (اب رساني) نلونه درزی کيږي او اوبه ورڅخه بهيږي چې بيا د گاز مات شوي نلونو او د قوي برق خراب لېنونوته اوبه رسيږي چې د اور اخستلو خطر زياتيږي. د اور د لگېدوپه وجه بيا ېو ډېر تباه كوونكئ خطر منځ ته راوړي. د ځمكې ښوېيدنه، د واورې ښوېيدنه، د ځمكې چاودېدل او يا په ځمكه كې مترونو مترونو پورې د چاود پوړۍ( زينې) جړېدل، دا ټول د تاوانونوعلتونه كېدې شي. د زلزلې په قوي ټكان باندې هغه ترسب شوي مېده شگه او يا خاوره د اوبو سره گډيږي او مايع ډوله عكس العمل ښكاره كوي، د ځمكې لاندې سامانونو ته تاوان رسيږي چې ودانۍ او يا ټوله ځمكه سره پرې كوي. په ساحلونو كې چېرته چې د زلزلې ساحه ده خصوصاً په بحرونو كې د زلزلې په وجه ډېرې اعظيمې څپې منځ ته راځي چې دا د تسونامي په نوم ياديږي او دغه عظيمې څپې هغه مناطقو ته چې په ټيټو ساحو كې واقع دي، ېو ډېر بې رحمه افتونه منځ ته راوړي.
مخكې د مخكې نه د ېوې زلزلې د كېدو اټكل كول:
د عالمانو د څېړنو له مخې، تر اوسه پورې د زلزلې دقيق وخت او ځائ معلومول نا ممكن دئ. مختلف معېن علتونه دي چې د څرنگوالي له مخې تر ډېر حده سړئ پوهېدائ شي. خو هر اړخيزه د زلزلې اساسي اندازه معلومول، كوم چې د زلزلې د داش په پروسه كې واقع كيږي، تر ډېر حده نا ممكن دئ چې سړئ د ېو زلزلې د كيدو اټكل په ېو معېن ځائ او يا په معېن وخت كې وكړي. خو بيا هم سړئ اجالتاً احتمالي څرگندونې كولاې شي. چې ېو نيم ددې څخه جيوفيزيكي ډېر لوې او بد بدلون دئ. د مثال په ډول: د زلزلې د ټكان سرعت، د ځمكې مېلان پېدا كول او يا د ډبرو الېكترو مگنيتي خواص. د احصايې له مخې نورې اساسي څرگندونې لكه د زلزلې د ټكان ارامېدل او بيا وروسته په ډېر لنډو كې ېوې ډېرې لوېې پېښې ته اشاره كول، د حېواناتو غېرارادي او تكرار تكرار رمباړې وهل چې دا هم په ډېرو لنډو كې د ېو لوې افت نښې دي.
د زلزلی په وخت کې باېد سړی څه وکړي؟
که سړی په ودانۍ کې وي، د زلزلی په وخت باېد کوښښ وکړي چې خپل سرونه د مېز، چيرکټ او يا تختونو لاندی پټ کړي.
او يا دی د دروازی په چوکاټ کې ودريږي. د هغو کړکۍ ګانو څخه ځان لری وساتي کوم چې ښيښه لري. که امکان ولري کوښښ دی وکړي چې تاکاو ته پناه وېسي.
که څوک بهر وي، نو د ونی، ودانۍ او د برق پاېو يا مزو څخه ځان لری وساتي.
هغه ساحی چې ډېر سخت د زلزلی تر اغيزی لاندی دي، باېد د ودانېو په جوړولو کې ډېره توجه وشي. يعنی د ودانۍ په لاندی برخه کې چېرته چې بنسټ ايښودل کيږي، اول د اوسپنی تختی ورکړل شي بيا د ربړ څخه تختی او دهغه په سر بيا د اوسپنی تخته او بيا د ودانۍ ته دوام ورکړل شي. او يا د فولادو څخه قوي سپرېنګونه د ودانۍ لاندی ورکړل شي. د ودانۍ په دننه کۍ ټول موبل (میز او چوکۍ) بايد د فرش او دېوال سره کلک شي.
په ښوونځېو کې دی زده کوونکو ته د زلزلی په برخه پوره معلومات ور کړل شي.
ددې پاڼې فارمټ جوړولو ته اړتیا ده - مرسته