Unusual number

Demonstration, with Cuisenaire rods, that the number 10 is an unusual number, its largest prime factor being 5, which is greater than √10 ≈ 3.16

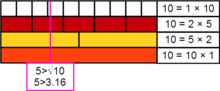
In number theory, an unusual number is a natural number n whose largest prime factor is strictly greater than ${\sqrt {n}}$.

A k-smooth number has all its prime factors less than or equal to k, therefore, an unusual number is non-${\sqrt {n}}$-smooth.

Relation to prime numbers

All prime numbers are unusual. For any prime p, its multiples less than p² are unusual, that is p, ... (p-1)p, which have a density 1/p in the interval (p, p²).

Examples

The first few unusual numbers are

2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 20, 21, 22, 23, 26, 28, 29, 31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 44, 46, 47, 51, 52, 53, 55, 57, 58, 59, 61, 62, 65, 66, 67, ... (sequence A064052 in the OEIS)

The first few non-prime (composite) unusual numbers are

6, 10, 14, 15, 20, 21, 22, 26, 28, 33, 34, 35, 38, 39, 42, 44, 46, 51, 52, 55, 57, 58, 62, 65, 66, 68, 69, 74, 76, 77, 78, 82, 85, 86, 87, 88, 91, 92, 93, 94, 95, 99, 102, ... (sequence A063763 in the OEIS)

Distribution

If we denote the number of unusual numbers less than or equal to n by u(n) then u(n) behaves as follows:

n	u(n)	u(n) / n
10	6	0.6
100	67	0.67
1000	715	0.72
10000	7319	0.73
100000	73322	0.73
1000000	731660	0.73
10000000	7280266	0.73
100000000	72467077	0.72
1000000000	721578596	0.72

Richard Schroeppel stated in the HAKMEM (1972), Item #29 that the asymptotic probability that a randomly chosen number is unusual is ln(2). In other words:

$\lim _{n\rightarrow \infty }{\frac {u(n)}{n}}=\ln(2)=0.693147\dots \,.$

External links

• Weisstein, Eric W. "Rough Number". MathWorld.