Talk:William F. Egan

This article must adhere to the biographies of living persons (BLP) policy, even if it is not a biography, because it contains material about living persons. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libellous. If such material is repeatedly inserted, or if you have other concerns, please report the issue to this noticeboard.

If you are a subject of this article, or acting on behalf of one, and you need help, please see this help page.

Biography: Science and Academia

	Biography portal This article is within the scope of WikiProject Biography, a collaborative effort to create, develop and organize Wikipedia's articles about people. All interested editors are invited to join the project and contribute to the discussion. For instructions on how to use this banner, please refer to the documentation.BiographyWikipedia:WikiProject BiographyTemplate:WikiProject Biographybiography articles
	This article is supported by the science and academia work group.

Electrical engineering

	Engineering portal This article is within the scope of WikiProject Electrical engineering, a collaborative effort to improve the coverage of Electrical engineering on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.Electrical engineeringWikipedia:WikiProject Electrical engineeringTemplate:WikiProject Electrical engineeringelectrical engineering articles
???	This article has not yet received a rating on the project's importance scale.

Years

 https://magazine.scu.edu/classnote/william-f-egan/

Additional refs

In 1981, describing high-order loops, William Egan conjectured that the addition of the zero pole to the loop filter's transfer function causes the hold-in and pull-in (acquisition) ranges to be theoretically infinite , i.e. that the hold-in and pull-in ranges of type 2 PLL are theoretically infinite: "The most common additional singularities are a low-frequency zero and a very-low-frequency pole (Fig.7.5d), essentially at zero frequency in many cases (see Fig. 7.5c), so that the hold-in range and acquisition range became theoretically infinite. That is, for the simplified model, they are infinite, although circuit limitations, such as finite VCO tuning range, will cause them to be finite".^[1]^: 176 In his book, published in 1998^[2]^: 192, he wrote that "We might also say that significant deviations occur when \Omega_{PI} is approached for the lag-lead filter; this is to be expected since the type 2 loops have infinite \Omega_{PI}." Later similar statement was formulated in various articles and books.

In 1986, Egan's conjecture (without ref to his original work) was published in Aguirre, S., Brown, D.H., and Hurd, W.J. (1986). Phase Lock Acquisition for Sampled Data PLL's Using the Sweep Technique. TDA Progress Report 4, 86, 95-102, page 96: "an analog PLL with a type II loop has an infinite pull-in range".

In Bandwidth Variation, A Fully Differential Phase-Locked Loop With Reduced Loop, 2011 the statement of Egan's conjecture is provided on page 22 without ref to Egan.

Amr M. Fahim noted in his book^[3]^: 6 that "in order to have an infinite capture range, an active filter must be used for the loop filter".

Similar statement can be found in (2005) Phase-Locked Loop Fundamentals. In: Clock Generators for SOC Processors. Springer, Boston, MA on page 6 (there is ref to Egan's book 1990 - see ref 13).

Since additional refs have been provided, thus I removed the BLP primary sources template.

nk (talk) 09:37, 4 June 2020 (UTC)[reply]

References

^ Egan, William F. (1981). Frequency synthesis by phase lock (1st ed.). New York: John Wiley & Sons.
^ Egan, William F. (1998). Phase-Lock Basics (1st ed.). New York: John Wiley & Sons.
^ Fahim, Amr M. (2005). Clock Generators for SOC Processors: Circuits and Architecture. Boston-Dordrecht-London: Kluwer Academic Publishers.

Additional explanations

I suggest to add the corresponding figure: Baseband model of type 2 analog PLLs.

Grand city building below beautiful blue sky and clouds — Baseband model of type 2 analog PLLs

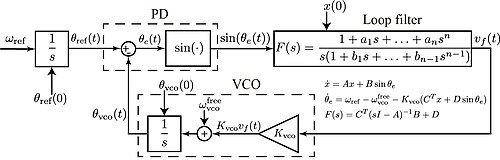
Milich64 (talk) 15:44, 22 June 2020 (UTC)[reply]

Feedback from New Page Review process

I left the following feedback for the creator/future reviewers while reviewing this article: Good start!.

North8000 (talk) 01:19, 30 June 2020 (UTC)[reply]

[1981-Egan-1] Egan, William F. (1981). Frequency synthesis by phase lock (1st ed.). New York: John Wiley & Sons.

[1998-Egan-2] Egan, William F. (1998). Phase-Lock Basics (1st ed.). New York: John Wiley & Sons.

[2005-Fahim-3] Fahim, Amr M. (2005). Clock Generators for SOC Processors: Circuits and Architecture. Boston-Dordrecht-London: Kluwer Academic Publishers.

[1]

[2]

[3]