Talk:Tensor/Rewrite
A tensor is a generalization of a scalar and a vector. In the language of tensors, a scalar is known as is a 0th-order tensor. As its magnitude is its sole component, it can be represented by a single number, said magnitude, which can then be considered a 0-dimensional matrix. A vector is a 1st-order tensor. It is like an arrow going from a source point to another, and it's components are the coordinates of that end point relative to the source point. These components make up a 1-dimensional matrix. A 2nd-order tensor is a geometrical object representable by a 2-dimensional array (an n×n matrix) of scalar components, or a 1-dimensional array of vector components, an array of arrays being a 2-dimensional matrix. An order-k tensor can be represented as a k-dimensional array of components. The dimension or number of indices of the array that expresses the tensor is its order.
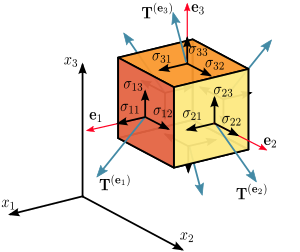
Although tensors are often represented as multidimensional arrays, they have intrinsic coordinate-free meaning that can be represented in different coordinate systems. In a different coordinate system, the same tensor takes a different matrix form. In the case of the stress tensor (see image right), under a change of coordinates, one would change which faces to consider not just which coordinate system is used to represent the vectors.
The nature of the transformation between coordinate systems is of interest to the study of tensors and is often the distinction that makes tensor analysis necessary rather than just using matrices. For example, if one refers to a "covariance tensor" rather than "covariance matrix", one is drawing attention to the fact that the covariance can be expressed in more than one coordinate system and likewise that there is no one "covariance matrix".
Additionally, there is the concept of the symmetry of a tensor, analogous to the concept of matrix symmetry.
Tensor Fields
[edit]A tensor field associates a tensor to points in space. A 0th-order tensor field is a scalar field and a 1st-order tensor field is a vector field.
A scalar field can be used to describe the density at each point in a solid. A heightmap is a scalar field whose magnitudes are converted to the Y values of points corresponding to each scalar. A vector field can be used to describe the velocity everywhere in a fluid. One common example of a second-order tensor field—the one from which the name arises—is stress in a solid. If a unit cube of material is supporting a unit force in compression along the Z axis, that stress can be described as a scalar, but suppose we now pull on the block with two units of force along the X axis while simultaneously pushing the X faces in opposite directions along the Y axis. While it is clear that we could apply such a stress to a block of material, it may not be clear how to quantify the stresses; there is tension and compression and shearing all in different directions. We could try to use several vectors to keep track of which directions are experiencing which stresses, but the elegant solution is to describe stress as a second-order tensor, representable in this case as a three-by-three symmetric matrix in which the i,j indices contain the stress on the i face in the j direction.


