Talk:Formal language
| This It is of interest to the following WikiProjects: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Archive 1: through June 15, 2009 Archive 2: June 16, 2009 through October 7, 2009 |
Infinite words
[edit]In the "Words over an Alphabet" section, a "word" is defined to be a "finite sequence" or "string." However, in other areas, it appears infinite sequences are permitted. For example, the set of all words contains countably infinite strings. As well, the section on constructions talks of infinitely long words. Does the "Words over an Alphabet" section need to be changed? 199.46.196.230 (talk) 22:29, 2 November 2015 (UTC)
- This article consistently talks about finitely long words only, even in the Constructions section. However, there are usually infinitely many such words, so is an infinite set of finite-length words. The article is correct in this respect. - Jochen Burghardt (talk) 07:05, 3 November 2015 (UTC)
Failure in "Operations on languages"-chart
[edit]According to
http://en.wikipedia.org/wiki/Recursively_enumerable_language
and
http://en.wikipedia.org/wiki/Recursive_language
RE-languages are not closed under set difference, recursive ones are. In the charts its the other way round.... —Preceding unsigned comment added by 79.205.161.224 (talk) 17:11, 8 November 2009 (UTC)
- I want to fix this. Can you tell me where it is in the article? — Carl (CBM · talk) 14:17, 9 November 2009 (UTC)
just fixed it myself, I wanted to be sure because I'm no native english speaking person...
sections edit-url:
http://en.wikipedia.org/w/index.php?title=Formal_language&action=edit§ion=5 —Preceding unsigned comment added by 79.205.170.133 (talk) 18:04, 9 November 2009 (UTC)
- I thought you were talking about set difference, which I don't see in the article. I have to think for a while about string substitution; I don't see why there is a problem with either recursive or r.e. languages there, but I might ahve misread the definition of substitution. Could you explain briefly or give some counterexample to help me understand? — Carl (CBM · talk) 20:10, 9 November 2009 (UTC)
well, maybe I got confused myself - I just hit the undo for now - its already pretty late over here... —Preceding unsigned comment added by 62.158.217.129 (talk) 22:14, 11 November 2009 (UTC)
Formal language vs. natural language
[edit]What are the differences between the formal languages and the natural languages? It cannot be grammar solely, as many natural languages such as English have their own defined grammar. --Abdull (talk) 15:17, 28 August 2010 (UTC)
- They are really totally different things, only vaguely similar. A formal language only consists of strings over a fixed alphabet, and the meaning (if one even exists) is not part of the formal language itself. A natural language is more than a collection of strings. It's even more than a structured collection of strings (written language) plus a structured collection of phoneme strings (spoken language), in many, many variants (dialects), with various correspondences between them. The meaning is also part of the language. And in some sense it's less than a formal language because for many strings it's not entirely clear whether they are grammatical or not. Some examples of borderline cases w.r.t. to the English language: "Let's write a poëm." "Have you been in 北京市 recently?" "Ceci n'est pas un double-entendre." "Ye five-and-twenty year-olde archaism." Or take any sentence that consists entirely of standard English words and follows the rules of English grammar precisely – but consists of more words than there are atoms in the universe. For a formal language, for each of these strings it would have to be decided once and for all whether they are part of the language or not. Hans Adler 15:35, 28 August 2010 (UTC)
- I'll probably keep repeating this until I'm blue in the face: I disagree with your formulation. A formal language is a language with a formal (i.e. mathematical) definition; a language (formal language theory) is what this article and your reply here are devoted to, but such a thing is usually just called a language, not a formal language, and it is a related, but clearly different notion in any case. The two notions should be clearly separated because most of the discussion on this page arises from confusing the two; as far as I'm concerned, they should have their own separate articles (full of cross-references). Rp (talk) 11:39, 30 August 2010 (UTC)
- I could make sense of your post by looking at your archived posts, but I am not sure your distinction is as important as you are making it. It happens all the time in mathematics that a certain type of structure is studied in a pure form, but also arises in applications, where it carries extra structure and extra meaning that is important for the application but not necessarily reflected by use of a different name. I can see some arguments for the POV that a language in the sense of formal language theory is the pure structure, while a formal language, as it arises in other contexts, is the applied thing which is typically a language in the former sense plus extra structure of one kind or another. Under this POV formal languages would not have a precise mathematical definition (unless it is something like "language plus arbitrary extra structure"). But I have never seen any source that discusses both languages and formal languages and distinguishes them. Therefore it seems more natural to me to assume that "language" is an abbreviation for "formal language" which is generally used in formal language theory, in the same way that in some contexts "group" is an abbreviation for "algebraic group" or "topological group". Hans Adler 12:09, 30 August 2010 (UTC)
- I agree, except that it's the other way round: formal language theory is devoted solely to studying the possible form of language and how to describe it, which explains its extremely narrow definition of language, excluding structure and excluding meaning, which are intrinsic properties of language in every other context of use of the term that I've ever seen. If you haven't been subjected to formal language theory, this distinction is nearly impossible to grasp; if you have, it should be easier, except that computer scientists and mathematicians tend to confuse formal definitions of terms with everyday use of the same terms. I believe this (lack of) distinction is what creates and recreates the confusing discussions on this talk page and the confounding of notions within the article itself. Rp (talk) 21:03, 30 August 2010 (UTC)
- I always thought a formal language was a set of strings over a finite alphabet, and of course there are such sets, most of them undefinable in the sense of definable real number. Natural language is completely different, and as a concept it's more from biology or psychology than mathematics. There's no way to pin down exactly what English is, not because it's mathematically undefinable, but because we each have our own idiolect that is constantly changing. 67.119.3.248 (talk) 17:17, 1 September 2010 (UTC)
- I agree, except that it's the other way round: formal language theory is devoted solely to studying the possible form of language and how to describe it, which explains its extremely narrow definition of language, excluding structure and excluding meaning, which are intrinsic properties of language in every other context of use of the term that I've ever seen. If you haven't been subjected to formal language theory, this distinction is nearly impossible to grasp; if you have, it should be easier, except that computer scientists and mathematicians tend to confuse formal definitions of terms with everyday use of the same terms. I believe this (lack of) distinction is what creates and recreates the confusing discussions on this talk page and the confounding of notions within the article itself. Rp (talk) 21:03, 30 August 2010 (UTC)
- I could make sense of your post by looking at your archived posts, but I am not sure your distinction is as important as you are making it. It happens all the time in mathematics that a certain type of structure is studied in a pure form, but also arises in applications, where it carries extra structure and extra meaning that is important for the application but not necessarily reflected by use of a different name. I can see some arguments for the POV that a language in the sense of formal language theory is the pure structure, while a formal language, as it arises in other contexts, is the applied thing which is typically a language in the former sense plus extra structure of one kind or another. Under this POV formal languages would not have a precise mathematical definition (unless it is something like "language plus arbitrary extra structure"). But I have never seen any source that discusses both languages and formal languages and distinguishes them. Therefore it seems more natural to me to assume that "language" is an abbreviation for "formal language" which is generally used in formal language theory, in the same way that in some contexts "group" is an abbreviation for "algebraic group" or "topological group". Hans Adler 12:09, 30 August 2010 (UTC)
- I'll probably keep repeating this until I'm blue in the face: I disagree with your formulation. A formal language is a language with a formal (i.e. mathematical) definition; a language (formal language theory) is what this article and your reply here are devoted to, but such a thing is usually just called a language, not a formal language, and it is a related, but clearly different notion in any case. The two notions should be clearly separated because most of the discussion on this page arises from confusing the two; as far as I'm concerned, they should have their own separate articles (full of cross-references). Rp (talk) 11:39, 30 August 2010 (UTC)
- I really think it depends on the context in which you encounter the term. Rp (talk) 23:46, 26 December 2010 (UTC)
Operations on other languages
[edit]The table of operations on languages is helpful but limited to "classical" formal languages (REG, DCFL, CFL, CSL, R, RE). It would be nice to include other classes of languages as well:
- Linear languages (LIN) which are between REG and CFL. There is also DLIN between REG and DCFL. — Preceding unsigned comment added by JakobVoss (talk • contribs) 13:21, 19 April 2011 (UTC)
- Visibly pushdown language (VPL) which are between REG and DCFL. Unlike DCFL they are closed under most operations. VPL are equivalent to so called nested words and regular tree grammar.
- Tree-adjoining grammars (TAG) which are between CFL and CSL. TAG and equivalent formalisms are often called mildly context-sensitive languages.
- Growing context-sensitive languages (GCSL) which are between CFL and CSL and in P. — Preceding unsigned comment added by JakobVoss (talk • contribs) 11:10, 19 April 2011 (UTC)
The term 'formal system' should do
[edit]I know I'm flogging an archived horse, but the present text is still assuming logic as the context in places. In particular, I don't think the term 'formal system' is widely used outside that context and the term "well-formed formula" is specific to logic (although the concept applies elsewhere). Rp (talk) 13:45, 19 December 2011 (UTC)
Form
[edit]What does "form" exactly/literally mean as it appears in the expression of "formal language"?
What is the difference between form and shape?
In the very beginning of this article, these questions should be answered. And a link to Wiktionary is not enough. --98.196.232.128 (talk) 22:39, 14 March 2012 (UTC)
- "Form" may have many meanings unrelated to "shape", and "formal" does not usually mean anything close to "shapely". See Formalism (mathematics) for something closer to the meaning in context. —David Eppstein (talk) 23:20, 14 March 2012 (UTC)
- I read that article and many othersrelated to it. Nop! I still don't understand. And it is still necessary at the beginning of (this) article.
- By the way, I know shape and form are two different concepts. But the distinction is neccessary for the sake of the article. In many languages, "shape" and "form" are carried by same word.--98.196.232.128 (talk) 01:07, 15 March 2012 (UTC)
- I don't see the point of explaining the etymology at the start of the article. We are not a dictionary. And in any case it is not necessary to understand "form" in order to understand "formal language" any more than it is necessary to understand "beg" in order to understand "beginning". It's just irrelevant. —David Eppstein (talk) 01:10, 15 March 2012 (UTC)
- I recently added an introduction to the Dutch pendant of this article (try Google Translate if you don't read Dutch) to make the relationship between the different uses of the term formal language clearer, and I think doing the same thing here would help avoid a lot of the confusion we're seeing here. What do you think? Rp (talk) 14:49, 15 March 2012 (UTC)
- Mr. David Eppstein, if you ever read a few Wikipedia articles, you will notice that most of them has a section describing the meaning of the words appearing in the title (name of the phenomenon). If you ever read a few more articles, you will notice that even etymologies are given. So, the people you call as "we" -I think- are not Wikipedists.
- Rp, thank you for Dutch Wiki article. It's very kind of you putting the link in Google Translate. I read Dutch article in English. It is far better than this English one. I started to understand. Thanks to you and Google translate.
- One interesting expression was this: "a formal language is an artificial language whose shape and often the meaning exactly is recorded". So, here comes "shape"!!! Who says shape is irrelevant? There is also an expression: "The formal language theory ... is dedicated to the study of mathematical formalisms for the form ( syntax ) of expressions in formal languages to ...". Therefore form is "the shape of a language which are also called syntax".
- Therefore, we have a definition for "form" as it appears in "formal" of the "formal language." Since "formal" means "relating to the form of something", the menaing of the word "form" is essential for the validity and understandibility of this article.
- Finally, I suggest putting my definition of "form" in the beginning of the article. But English is not my first language. Therefore, a possible better definition might be even better.--98.196.232.128 (talk) 02:21, 16 March 2012 (UTC)
- I'll try a real translation. Rp (talk) 09:04, 16 March 2012 (UTC)
Well ... I haven't. The gist of it: formal language theory is the formal study of the form of language. Here, form is syntax and is used in opposition to meaning (semantics), which formal language theory is not concerned with. The study is formal in that it uses mathematical formalisms to describe the syntax of language. Rp (talk) 09:52, 3 July 2017 (UTC)
Content at Object theory
[edit]Following a recent discussion, Object theory was blanked and turned into a disambiguation page. Of all pages I could think of, it seems to me that its previous content was most relevant to this page, so editors may want to consult the page history for anything salvageable. Felix QW (talk) 11:37, 4 July 2022 (UTC)
- This is a rather baffling page indeed. Direct link for the curious. I don't think formal languages is really the right target, but I don't much of the content is salvageable anyway. It's all using obscure terminology (probably from Kleene's book) and the few references are either generic or obscure. Better to have articles describing these concepts in the proper modern terminology. Caleb Stanford (talk) 14:42, 4 July 2022 (UTC)
- The content seems appropriate for a page on formal systems, not formal language theory. Rp (talk) 20:59, 11 July 2022 (UTC)
- To me it looks closer to Structure (mathematical logic). —David Eppstein (talk) 22:16, 11 July 2022 (UTC)
- The content seems appropriate for a page on formal systems, not formal language theory. Rp (talk) 20:59, 11 July 2022 (UTC)
Error in examples
[edit]The first bulletpoint in the section Examples contains does not contain -or "=". This should probably be does not contain "+" or "=", but I'll leave that to someone with more knowledge on the subject to correct. 159.100.126.214 (talk) 13:09, 9 September 2022 (UTC)
- Thank you! Corrected. Felix QW (talk) 14:29, 9 September 2022 (UTC)
Mention the topic of equivalence of two grammars
[edit]There's the concept of equivalence of two grammars, and the respective article (Equivalence (formal languages)) really should be linked somewhere in here. Shuween (talk) 17:16, 7 March 2023 (UTC)
- The article you linked has issues in the lead that are unresolved for 9 years; so I consider it essentially unmaintained and hardly helpful. In the general article about formal languages (defined by what ever formalism, not necessarily a grammar, let alone a context-free one), not much can be said about equivalence. In context-free grammar the remark you suggest is already present; in regular grammar, I just added it, inspired by your above post. - Jochen Burghardt (talk) 18:01, 7 March 2023 (UTC)
Questioning redirect 'Symbolic system'
[edit]Why ought Symbolic system redirect here? The term 'symbol' or 'symbolic' do not arise on this page in the first place FatalSubjectivities (talk) 15:12, 30 March 2023 (UTC)
- I think this is a leftover from a past editor who seemed to think this page was about formal systems, as still reflected in the present sentence:
In logic and the foundations of mathematics, formal languages are used to represent the syntax of axiomatic systems, and mathematical formalism is the philosophy that all of mathematics can be reduced to the syntactic manipulation of formal languages in this way.
- Clearly, this is just about correct, but not 100%, and I think this article should probably do a better job of explaining that. Part of the problem is that formal language really isn't a technical term I've seen anybody use, so it's not clear to me what this article should and should not cover. If we rename it to Language (formal language theory), the subject will be 100% unambiguous, and editing the article will become easier. I'm not going to do it because it's just going to be reverted, but I think it's what should be done. Rp (talk) 15:58, 1 April 2023 (UTC)
Finite or infinite alphabet
[edit]An alphabet, in the context of formal languages, can be any set, although it often makes sense to use an alphabet in the usual sense of the word, or more generally any finite character encoding such as ASCII or Unicode. The elements of an alphabet are called its letters. An alphabet may contain an infinite number of elements;[note 1] however, most definitions in formal language theory specify alphabets with a finite number of elements, and most results apply only to them.
Notes
- ^ For example, first-order logic is often expressed using an alphabet that, besides symbols such as ∧, ¬, ∀ and parentheses, contains infinitely many elements x0, x1, x2, … that play the role of variables.
This seems to me to contradict itself by requiring that character encoding sets by finite while alphabets may be infinite. I would prefer other editors more familiar with the topic make any necessary changes; I'm not sufficiently familiar with this topic to write with precision on it. Daask (talk) 15:56, 5 October 2023 (UTC)
- Character encoding sets such as ASCII or Unicode are finite; that is not a requirement, just an observation. They are examples of things that one could use as an alphabet, but not the only examples. The infinite alphabet described in the footnote is another example. —David Eppstein (talk) 16:04, 5 October 2023 (UTC)
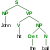
Update the tree?
[edit]The tree in the example ("Colorless green ideas sleep furiously") is not particularly theoretically up-to-date (most modern syntax does not use S, and would prefer DP, vP shells and so on). I know that this page is about formal languages more generally, but the caption "Structure of the syntactically well-formed, although nonsensical, English sentence" refers to the structure of the English sentence. This gives the impression that the structure of English sentences (as opposed to, e.g. toy languages modeled on English as used in NLP textbooks) is like this, which is inaccurate for most modern linguists.
On the other hand, if the purpose is just to show a tree of any formal language, why include the empty X' levels (e.g. N'-N'-N) at all? To someone coming from a non-linguistic background, these could also be confusing, particularly as this tree has so many of them. The saved vertical space could also be used to incorporate the rewrite rules in Chomsky Normal Form used to generate the tree (which would be much simpler if the bar-levels were removed). BobEret (he/him) (talk) 18:29, 9 January 2024 (UTC)
- You have a good point. I think the right answer is the Wikipedia answer: source the material. Use a tree from a published article, refer to it, and explain the context. Rp (talk) 13:14, 13 January 2024 (UTC)
- ... and [in this case] additionally: provide an image that shows your new tree. - Jochen Burghardt (talk) 19:01, 14 January 2024 (UTC)
- C-Class level-4 vital articles
- Wikipedia level-4 vital articles in Mathematics
- C-Class vital articles in Mathematics
- C-Class Computing articles
- Mid-importance Computing articles
- All Computing articles
- C-Class Computer science articles
- High-importance Computer science articles
- WikiProject Computer science articles
- C-Class mathematics articles
- High-priority mathematics articles
- C-Class Linguistics articles
- Unknown-importance Linguistics articles
- WikiProject Linguistics articles