Talk:Quasiregular polyhedron
| This article is rated C-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||||||||||||
| |||||||||||||||||||||
Inconsistencies
[edit]By the definition here, "A polyhedron which has regular faces and is transitive on its edges is said to be quasiregular", all regular polyhedra are quasiregular. By the definition at Polyhedron, "vertex-transitive and edge-transitive (and hence has regular faces) but not face-transitive", no regular polyhedron is quasiregular. Thus these two definitions are inconsistent. Furthermore, the enumeration of convex quasiregular polyhedra given here, which includes the octahedron but excludes the other regular polyhedra, is inconsistent with both definitions.
In fact the two external sites cited disagree as to whether the octahedron should be regarded as quasiregular. But both agree that to be quasiregular, faces with n sides must alternate with faces with m sides at each vertex -- implying an even number of faces at each vertex. Then the octahedron is quasiregular or not, depending on whether you allow n=m or not, but the other regular polyhedra (having 3 or 5 faces at each vertex) are not.
(posted by 24.58.33.52 on 06:06, 3 January 2008).
- Hi, you are quite right about the inconsistencies. The literature on quasiregular polyhedra is pretty sparse, but it appears to be one of those many areas where geometers define one thing and then describe something else. One of the difficulties is that there are several interesting quasiregular properties, but nobody has ever methodically figured out which properties are fundamental and which are consequences of these. Feel free to make clarifications as to the nature of the muddle.
- As for the octahedron, it can be seen as quasiregular by the definition at Polyhedron, if we colour alternate faces black and white so there are two kinds - a figure sometimes also called the tetratetrahedron.
- And as for other web sites, they are for the most part a terrible load of rubbish. Mathworld perpetuates many shameful myths about polyhedra. George Hart is a lot more reliable, though his classification of quite so many star polyhedra as quasiregular is unusual (I happen to agree with him, but that is a long and continuing story).
- HTH -- Steelpillow (talk) 12:55, 3 January 2008 (UTC)
Missing entries?
[edit]If non-convex polyhedra with non-convex vertex figures count, there's a number missing, firstly the edge-sharing forms (is there an "official" term?) of the pictured five:
- tetrahemihexahedron
- cubohemioctahedron & octahemioctahedron
- small dodecahemidodecahedron & small icosihemidodecahedron
- great dodecahemidodecahedron & great icosihemidodecahedron
- small dodecahemicosahedron & great dodecahemicosahedron
Also, these have only singly symmetrical but nevertheless alternating vertex figures. Dunno if that's an additional problem.
- small rhombihexahedron, great rhombihexahedron
- small rhombidodecahedron, great rhombidodecahedron
- rhombicosahedron
- small dodecicosahedron, great dodecicosahedron
Didn't want to add these directly for two reasons - the section for non-convex quasiregulahedrons is titled with "examples", and I notice the discussion on what the authorities consider quasiregular anyway... --Tropylium (talk) 19:28, 20 February 2008 (UTC)
- You have the right idea. The first list are indeed quasiregular (though the second list are not - they do not have edges all wthin a single symmetry orbit). We can also find quasiregular examples among the apeirohedra - plane tessellations and infinite skew polyhedra. Trouble is, none of this seems to have been published in an adequate reference (It's on George Hart's website but AIUI personal websites are deemed inadequate). A few months ago I submitted a paper on exactly this to the Mathematical Intelligencer, so we shall have to wait and see. -- Steelpillow (talk) 20:58, 22 February 2008 (UTC)
More missing entries
[edit]under the list of convex quasi-regular polyhedra, it says the the cuboctohedron and the icosahedron are the only two. However in the category "Quasiregular Polyhedra", it lists the rhombic dodecahedron and rhombic tricontahedron as well. Shouldn't they be included then? —Preceding unsigned comment added by Timeroot (talk • contribs) 17:39, 4 July 2008 (UTC)
- They're given here under Quasiregular_polyhedron#Quasiregular_duals. Tom Ruen (talk) 05:18, 5 July 2008 (UTC)
- See also the remark in that section, about differences of opinion as to whether these two polyhedra are quasiregular or not. Cromwell regards them as quasiregular, while Coxeter et. al. do not. -- Cheers, Steelpillow (Talk) 11:50, 5 July 2008 (UTC)
Lead needs to be more accessible
[edit]The lead for this uses too much technical jargon. Move the mathematical definition into the article and make the lead into an introduction which is accessible to an intelligent, well educated non-mathematician.
I'm trained as an engineer and I couldn't make head nor tail of this intro. filceolaire (talk) 09:51, 23 November 2009 (UTC)
- A worthy complaint! Hopefully better now? Tom Ruen (talk) 10:22, 23 November 2009 (UTC)
- Much better. Thanks. filceolaire (talk) 12:54, 23 November 2009 (UTC)
Two errors in second diagram
[edit]In the diagram "Regular and quasiregular figures" there are two errors.
In the third column, second row, the Schläfli symbol is missing. It should be {3 3} arranged vertically.
In the fourth column, fourth row, the caption should not be "pentagonal tiling". This thing is quasiregular not regular. Maybe "tetrapentagonal tiling"?
I haven't time to fix these now. Maproom (talk) 13:59, 18 February 2010 (UTC)
- Thanks. I have fixed the tetrapentagonal tiling. The Schläfli symbol poses a problem. These symbols are supposed to be unique to a given figure. Clearly, applies to two of the examples given, thus providing a counter-example to long-held mathematical folk lore. I think that all we can do here is to faithfully reflect published sources, imperfect as they are. -- Cheers, Steelpillow (Talk) 16:38, 18 February 2010 (UTC)
- The 5.4.5.4 tiling does not belong in that table! It ought to show {5,4} as , the rectification of {5,5}. —Tamfang (talk) 22:06, 18 February 2010 (UTC)
- Yes, it belongs in the table above - that will mess up somebody's nice layout. The appropriate "single-height" symbol is {5.4}2, and none other. -- Cheers, Steelpillow (Talk) 20:34, 19 February 2010 (UTC)
- with (), not {} —Tamfang (talk) 02:43, 3 July 2023 (UTC)
- Yes, it belongs in the table above - that will mess up somebody's nice layout. The appropriate "single-height" symbol is {5.4}2, and none other. -- Cheers, Steelpillow (Talk) 20:34, 19 February 2010 (UTC)
- The 5.4.5.4 tiling does not belong in that table! It ought to show {5,4} as , the rectification of {5,5}. —Tamfang (talk) 22:06, 18 February 2010 (UTC)
Gallery of duals
[edit]I have moved this from the article because the references given do not include the majority of these figures. Indeed, they do not consistently recognise all the original "parents" as quasiregular - the most reliable sources such as Coxeter do not.
As an example of the problem, the tetrahemihexahedron does not have a Schläfli symbol distinct from that of the cuboctahedron. Coxeter did not regard it as quasiregular, even though he sometimes gave definitions of quasiregularity which are consistent with it. We are once again into the inconsistencies of modern theory, and we must be careful to avoid wp:or. -- Cheers, Steelpillow (Talk) 18:44, 28 February 2010 (UTC)
- here is the bit I have moved
The nonconvex ones are:
- The medial rhombic triacontahedron,
- the great rhombic triacontahedron,
- the duals of the hemipolyhedra,
- and the three triambic icosahedra, duals of the three ditrigonal polyhedra.
pictured below.
 Medial rhombic triacontahedron V5.5/2.5.5/2 |
 Great rhombic triacontahedron V3.5/2.3.5/2 |
 Tetrahemihexacron V3.4.3/2.4 |
 Octahemioctacron V3.6.3/2.6 |
 Hexahemioctacron V4.6.4/3.6 |
 Small icosihemidodecacron V3.10.3/2.10 |
 Small dodecahemidodecacron V5.10.5/4.10 |
 Great icosihemidodecacron V10/3.3.10/7.3 |
 Great dodecahemidodecacron V5/2.10/3.5/3.10/3 |
 Great dodecahemicosacron V5.6.5/4.6 |
 Small dodecahemicosacron 5/2.6.5/3.6 |
 Small triambic icosahedron V5.5/3.5.5/3.5.5/3 |
 Medial triambic icosahedron V3.5/2.3.5/2.3.5/2 |
 Great triambic icosahedron V(3.5.3.5.3.5)/2 |
chiral link
[edit]I'll bite. Why did David Eppstein (talk · contribs) add Chiral polytope to the See also? —Tamfang (talk) 22:46, 30 August 2012 (UTC)
- Because his discussion of abstract chiral polytopes discusses their relation to quasiregularity? — Cheers, Steelpillow (Talk) 13:02, 1 September 2012 (UTC)
Sixfold vertices
[edit]Do any of the sources referenced explicitly state that sixfold vertices can be treated as quasiregular? I have only ever seen quasiregularity discussed in the context of fourfold vertices. — Cheers, Steelpillow (Talk) 11:26, 29 August 2013 (UTC)
- Why wouldn't they be treated as quasiregular? Of course there are no ditrigonal polyhedra, regular or quasiregular; but that's a matter of what can up up to 360 degrees, not of definition. Maproom (talk) 12:16, 29 August 2013 (UTC)
- Actually, there are ditrigonal polyhedra. Even if we ban coplanar faces, using star polygons solves the problem, as they can have internal angles smaller than 60°. Additionally, the faces do not all have to circle forwards, and there is nothing stopping them from wrapping round the vertex more than once. Thus there exist ditrigonal polyhedra: the quasiregular ones are the small ditrigonal icosidodecahedron, ditrigonal dodecadodecahedron, and great ditrigonal icosidodecahedron. Double sharp (talk) 13:56, 14 April 2014 (UTC)
- I was wrong, at least in part. In their classic paper on Uniform polyhedra, Coxeter et. al. give a definition of quasiregularity compatible with sixfold vertices and identify a number of such polyhedra. But I was also right in part. In that same paper they describe nine polyhedra as "semi-regular" even though they appear to meet the given definition of quasiregularity. (These are all "hemi" polyhedra having faces passing through their centres, hence their Schwarz triangles and associated Wythoff symbols do not display the characteristics of quasiregularity even though the polyhedra themselves do. Presumably this is why they were missed.) If we treat these as quasiregular when Coxeter et. al. (or anybody else) did not, we are guilty of WP:OR. If the fact that these polyhedra meet the definition cannot be referenced, then however true and obvious we might think it, saying so is WP:OR. This also applies to tilings of the plane having sixfold vertices, which I have not seen addressed in this context. I admit I have not read widely on such tilings, so good sources might be out there, but are they? That both answers your first question and provides counterexamples to your subsequent assertion. I assume you mean, there are no convex ditrigonal polyhedra in Euclidean space. — Cheers, Steelpillow (Talk) 14:24, 29 August 2013 (UTC)
- George W. Hart lists non-convex ditrigonals as quasi-regular: [1]. — Stannic (talk) 15:51, 29 August 2013 (UTC)
- George's website is self-published and, for the most part if not all, is not peer-reviewed. As such we cannot regard it as an authoritative source. It can at best be used to support material from such sources. — Cheers, Steelpillow (Talk) 18:04, 29 August 2013 (UTC)
- George W. Hart lists non-convex ditrigonals as quasi-regular: [1]. — Stannic (talk) 15:51, 29 August 2013 (UTC)
- Coxeter's 1954 paper [2] (Section 7), title "The regular and quasiregular polyhedra p | q r" says "p | q 2" are regular, and all the others with this Wythoff symbol are quasiregular, including right triangles "2 | p q" and in general triangles none are regular, all 3 singularly active mirrors make quasiregulars. Tom Ruen (talk) 21:08, 29 August 2013 (UTC)
- The Hemipolyhedron don't qualify as quasiregular because Wythoff symbol, p/(p − q) p/q | r, shows two active mirrors. I notice at Small icosihemidodecahedron it says: It is given a Wythoff symbol, 3/2 3 | 5, but that construction represents a double covering of this model. Tom Ruen (talk) 22:04, 29 August 2013 (UTC)
- Here's a graphic File:Vertex figures.png based on Johnson's names at List of uniform polyhedra by vertex figure (Only online source Mathworld I think, [3]). So it show the quasiregular with a rectangular vertex figure, and (hemi-polyhedra) as versi-regular with crossed-rectangle. Tom Ruen (talk) 23:01, 29 August 2013 (UTC)
- Johnson (2000) classified uniform polyhedra according to the following:
- Regular (regular polygonal vertex figures): pq, Wythoff symbol q|p 2
- Quasi-regular (rectangular or ditrigonal vertex figures): p.q.p.q 2|p q, or p.q.p.q.p.q, Wythoff symbol 3|p q
- Versi-regular (orthodiagonal vertex figures), p.q*.-p.q*, Wythoff symbol q q|p
- Truncated regular (isosceles triangular vertex figures): p.p.q, Wythoff symbol q 2|p
- Versi-quasi-regular (dipteroidal vertex figures), p.q.p.r Wythoff symbol q r|p
- Quasi-quasi-regular (trapezoidal vertex figures): p*.q.p*.-r q.r|p or p.q*.-p.q* p q r|
- Truncated quasi-regular (scalene triangular vertex figures), p.q.r Wythoff symbol p q r|
- Snub quasi-regular (pentagonal, hexagonal, or octagonal vertex figures), Wythoff symbol p q r|
- Prisms (truncated hosohedra),
- Antiprisms and crossed antiprisms (snub dihedra)
- @Tom, You say that the hemipolyhedra don't qualify because of their Wythoff symbols (on the sphere). I'm sorry, but where in the definition of quasiregularity does it demand a specific form of Wythoff symbol on the sphere? My understanding of quasiregularity is that its definition is based on the arrangement of faces around each vertex. FYI the Mathworld reference to Johnson (2000) is to a draft ms on Uniform Polytopes that is still yet to be published, a classic example of why websites like Mathworld are not reputable sources. Johnson's classification scheme also appears to be used in the List of uniform polyhedra by vertex figure, but there is no proper citation of him (or of anyone else!) on that page. — Cheers, Steelpillow (Talk) 11:11, 30 August 2013 (UTC)
- In fact, with the exception of the orientable octahemioctahedron, these Wythoff symbols do not even represent the hemipolyhedra themselves, but rather degenerate versions of them where all elements are doubled. Double sharp (talk) 13:58, 14 April 2014 (UTC)
- @Tom, You say that the hemipolyhedra don't qualify because of their Wythoff symbols (on the sphere). I'm sorry, but where in the definition of quasiregularity does it demand a specific form of Wythoff symbol on the sphere? My understanding of quasiregularity is that its definition is based on the arrangement of faces around each vertex. FYI the Mathworld reference to Johnson (2000) is to a draft ms on Uniform Polytopes that is still yet to be published, a classic example of why websites like Mathworld are not reputable sources. Johnson's classification scheme also appears to be used in the List of uniform polyhedra by vertex figure, but there is no proper citation of him (or of anyone else!) on that page. — Cheers, Steelpillow (Talk) 11:11, 30 August 2013 (UTC)
Quasiregular polychora and honeycombs
[edit]In Regular Polytopes (book) Coxeter says {4,3,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() is the only regular honeycomb in Euclidean 3-space, and h{4,3,4},
is the only regular honeycomb in Euclidean 3-space, and h{4,3,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]() is the only quasiregular honeycomb. So I'm not sure of the full definition, but in this case, it has a quasiregular vertex figure. So from that case alone here's a list of qualifying forms, each has alternating of two types of cells, although they are also regular if the two cells are the same type (like a checkerboard). Tom Ruen (talk) 01:23, 13 October 2013 (UTC)
is the only quasiregular honeycomb. So I'm not sure of the full definition, but in this case, it has a quasiregular vertex figure. So from that case alone here's a list of qualifying forms, each has alternating of two types of cells, although they are also regular if the two cells are the same type (like a checkerboard). Tom Ruen (talk) 01:23, 13 October 2013 (UTC)
Quasiregular 4D polytopes:
- (also regular)






 =
= 





 =
= 



 =
= 



 , {3,3,4} = {3,31,1} tet-tet {3,3}-{3,3} - vertex figure is octahedron or tetratetrahedron,
, {3,3,4} = {3,31,1} tet-tet {3,3}-{3,3} - vertex figure is octahedron or tetratetrahedron, 




Quasiregular 3D Euclidean honeycombs






 =
= 



 =
= 



 h{4,3,4} tet-oct {3,3}-{3,4} - vertex figure is cuboctahedron,
h{4,3,4} tet-oct {3,3}-{3,4} - vertex figure is cuboctahedron, 




- (also regular)






 =
= 



 =
= 



 {4,31,1} = {4,3,4} cube-cube {4,3}-{4,3} - vertex figure is octahedron or tetratetrahedron,
{4,31,1} = {4,3,4} cube-cube {4,3}-{4,3} - vertex figure is octahedron or tetratetrahedron, 




Quasiregular 3D compact hyperbolic honeycombs






 =
= 



 =
= 



 h{4,3,5} tet-icos {3,3}-{3,5} - vertex figure is icosidodecahedron,
h{4,3,5} tet-icos {3,3}-{3,5} - vertex figure is icosidodecahedron, 




- (also regular)




 =
= 



 =
= 





 {5,31,1} = {5,3,4} dodec-dodec {5,3}-{5,3} - vertex figure is octahedron or tetratetrahedron,
{5,31,1} = {5,3,4} dodec-dodec {5,3}-{5,3} - vertex figure is octahedron or tetratetrahedron, 




Quasiregular 3D Paracompact_uniform_honeycombs






 =
= 



 h{4,3,6} tet-tri {3,3}-{3,6} - vertex figure is trihexagonal tiling,
h{4,3,6} tet-tri {3,3}-{3,6} - vertex figure is trihexagonal tiling, 




- (also regular)






 =
= 



 {3,41,1} = {3,4,4} oct-oct {3,4}-{3,4} - vertex figure is square tiling or checkerboard,
{3,41,1} = {3,4,4} oct-oct {3,4}-{3,4} - vertex figure is square tiling or checkerboard, 




- (also regular)






 =
= 



 {6,31,1} = {6,3,4} hex-hex {6,3}-{6,3} - vertex figure is octahedron or tetratetrahedron,
{6,31,1} = {6,3,4} hex-hex {6,3}-{6,3} - vertex figure is octahedron or tetratetrahedron, 










 =
= 



 =
= 



 h{4,4,3} cube-square {4,3}-{4,4} - vertex figure is cuboctahedron,
h{4,4,3} cube-square {4,3}-{4,4} - vertex figure is cuboctahedron, 




- (also regular)






 =
= 





 =
= 



 =
= 



 h{4,4,4} = {4,4,4} square-square {4,4}-{4,4} - vertex figure is square tiling or checkerboard,
h{4,4,4} = {4,4,4} square-square {4,4}-{4,4} - vertex figure is square tiling or checkerboard, 




- (also regular)




 =
= 





 , {p,3[3]} = {p,3,6} (p=3,4,5,6) {p,3}-{p,3} - vertex figure is {3[3]} = {3,6},
, {p,3[3]} = {p,3,6} (p=3,4,5,6) {p,3}-{p,3} - vertex figure is {3[3]} = {3,6}, 


According Norman Johnson (in private communication)
A recursive definition of quasi-regular, which agrees with how the term is used by Coxeter, is as follows:
- A polygon is quasi-regular if its symmetry group is transitive on the vertices. [regular
and truncated
]
- An n-polytope (n > 2) is quasi-regular if its symmetry group is transitive on the vertices and its vertex figures are quasi-regular.
Rectified polyhedra [1-ring Coxeter diagram] are quasi-regular, but so are the ditrigonary polyhedra, which are not obtained by rectification. For n > 3, rectified regular n-polytopes are generally not quasi-regular.
- Tom Ruen (talk) 03:31, 13 October 2013 (UTC)
- Well, Tom, that's all very fascinating but it appears to be unpublished. As such it is WP:OR and has no place here. — Cheers, Steelpillow (Talk) 09:14, 14 October 2013 (UTC)
- As I said I only have explicit source statement for the Euclidean honeycomb h{4,3,4}, so that is defendable on the article. But for the full list above, that's why I put it here on the talk page. I'll continue looking for what else Coxeter said about Quasiregular honeycombs. Tom Ruen (talk) 09:30, 14 October 2013 (UTC)
- Eh? Coxeter does give a full definition in Regular Polytopes, p.69 (3rd ed.)! "A honeycomb is said to be quasiregular if its cells are regular while its vertex figures are quasiregular. This definition (cf. § 2·3) implies that the vertex figures are all alike, and that the cells are of two kinds, arranged alternately." Double sharp (talk) 11:35, 4 March 2015 (UTC)
- That's helpful, at least works for me for 3D honeycombs, Euclidean and hyperbolic, and 4D polychora as spherical honeycombs. Tom Ruen (talk) 12:02, 4 March 2015 (UTC)
- Eh? Coxeter does give a full definition in Regular Polytopes, p.69 (3rd ed.)! "A honeycomb is said to be quasiregular if its cells are regular while its vertex figures are quasiregular. This definition (cf. § 2·3) implies that the vertex figures are all alike, and that the cells are of two kinds, arranged alternately." Double sharp (talk) 11:35, 4 March 2015 (UTC)
Degenerate case
[edit]The common core of a dihedron and hosohedron would be a degenerate figure with n+2 faces (2 n-gons, n digons), 2n edges, and n vertices. It's not currently listed here. Should it be? Does it have a name? Joule36e5 (talk) 22:17, 27 January 2015 (UTC)
- Let's see - = = {n,2} (or




 =
= 



 =
= 



 ). So the regular dihedra are also quasiregular, with 2 colors, one for each hemisphere rather than a single color. So the way the dihedrons are colored now is actually quasiregular. Tom Ruen (talk) 22:28, 27 January 2015 (UTC)
). So the regular dihedra are also quasiregular, with 2 colors, one for each hemisphere rather than a single color. So the way the dihedrons are colored now is actually quasiregular. Tom Ruen (talk) 22:28, 27 January 2015 (UTC)
- "Does it have a name?" It's a (pentagonal, whatever) prism, isn't it? Maproom (talk) 22:49, 27 January 2015 (UTC)
- I think Tom's analysis is correct. Like the octahedron, dihedra have both regular and quasiregular colorings. I'd go further and suggest that even-numbered hosohedra do as well (depending on your definition of quasiregularity). But I'll bet you won't find any of that in any reliable source. The hosohedra degenerate to infinite prisms in Euclidean space, but these are not the same structures as the prism polyhedra. — Cheers, Steelpillow (Talk) 07:28, 28 January 2015 (UTC)
- Yes, I see now that Tom is right. A prism isn't quasiregular, it's just a truncated hosohedron. Maproom (talk) 08:05, 28 January 2015 (UTC)
- Hosohedra of the form {2,2q} would indeed be quasiregular: the colouring would be as shown at Hosohedron#Kaleidoscopic symmetry. You can imagine these improper forms on the table by adding a row at the top for {p,2} (the dihedra) and a column to the left for {2,2q} (the hosohedra). (But does {1,2} count as quasiregular? It would be a singular exceptional sense, because I don't see how {1,2q} would work for q > 1.) Double sharp (talk) 10:33, 28 January 2015 (UTC)
- {1,2q} may be constructed on the projective plane, where it is simply q lines through a point. I suppose one could call them projective hosohedra. The dual {2q,1} projective monohedron would be a single 2q-gon wrapped around a line subdivided into q segments. At this point, the wise among us begin to think, "hang on, do I have q or 2q edges here? I need to understand this kind of thing before I decide what is or is not a valid, or even degenerate, polytope". — Cheers, Steelpillow (Talk) 11:02, 28 January 2015 (UTC)
- (All off-topic) I would call them hemishosohedra and hemidihedra. A hemidihedron has q edges, but its face has 2q edges. It is dodgy regarding such things as polyhedra, but they are perfectly respectable regular maps. Maproom (talk) 12:56, 28 January 2015 (UTC)
- OK, I think I see what you're describing. Can {1,q} and {q,1} exist for odd q? (I guess hemihosohedra and hemidihedra seem like reasonable terms, given the projective polyhedra like hemi-cubes.) Double sharp (talk) 06:00, 29 January 2015 (UTC)
- In general they cannot exist for odd q. You cannot draw n lines right through a point but with an odd number of segment ends meeting. Nor can you cut a polygon from inside a sheet of paper and end up with an odd number of cut sides when you add the sides of the polygon to the sides of the hole. Those are good names, it would be nice if they could be reliably sourced. — Cheers, Steelpillow (Talk) 12:14, 31 January 2015 (UTC)
- So I guess {1,1} would be the sole such case (and it is a weird one). I do wonder though if you can use rational numbers here, to create cases like {2,8/3}, {1,8/3} or their duals, as long as their numerators are even.
- This (p.163) seems to support this kind of use of the "hemi-" prefix, but unfortunately doesn't use it on the dihedra and hosohedra. The examples it gives are the hypercubes, orthoplices (spelling?), and the regular polyhedra and 4-polytopes/polychora (except of course the simplices). Double sharp (talk) 13:45, 31 January 2015 (UTC)
- I notice that spherical polyhedron already mentioned the cases {1,1}, {2p,1}, and {1,2p} (though calling the last two {2p,2}/2 and {2,2p}/2). It uses the names "hemi-dihedron" for {2p,1} and "hemi-hosohedron" for {1,2p}. I guess they can be considered cited, albeit at a slight stretch (both elements of the words are attested with the right meanings, but I can't find them used together to create this compound). Double sharp (talk) 08:20, 1 February 2015 (UTC)
- Regular map (geometry) uses the terms "hemi-dihedron" and "hemi-hosohedron", citing them to Coxeter: if this attribution is correct, there would no longer be any problems with these names. Double sharp (talk) 14:01, 2 February 2015 (UTC)
- I do not have Coxeter & Moser's cited book to hand but the Index has no mention of anything hemi while a search of a copy on Google Books provided no hits for either hemi or for hemicube. It is not looking good. — Cheers, Steelpillow (Talk) 15:00, 2 February 2015 (UTC)
- Coxeter lists {2p,2}/2 and {2,2p}/2 cases with no names, only as trivial elliptical maps, p 111 of Coxeter & Moser, 1957.
- Above I gave a source for "hemi-" alone and applied with the hypercubes, cross-polytopes, dodecahedron, icosahedron, 24-cell, 120-cell, and 600-cell: Abstract Regular Polytopes by McMullen and Schulte (2002), p.163; so those are all right. It's the hemi-dihedra and hemi-hosohedra that are still unsourced for now (their existence is certainly sourced – I know Coxeter mentions them – but I do not know if he names them, which is the unsourced part). Double sharp (talk) 14:12, 4 February 2015 (UTC)
- I find it was me who introduced the terms "hemi-dihedron" and "hemi-hosohedron" to the Regular map (geometry) article. I'm on holiday this week. When I get home I'll see if can source them to a reference book. Maproom (talk) 16:40, 2 February 2015 (UTC)
- Here's a reputable source for "hemi-hosohedron" and "hemi-dihedron".[1]section 2.3 Maproom (talk) 13:38, 6 February 2015 (UTC)
- I do not have Coxeter & Moser's cited book to hand but the Index has no mention of anything hemi while a search of a copy on Google Books provided no hits for either hemi or for hemicube. It is not looking good. — Cheers, Steelpillow (Talk) 15:00, 2 February 2015 (UTC)
- Regular map (geometry) uses the terms "hemi-dihedron" and "hemi-hosohedron", citing them to Coxeter: if this attribution is correct, there would no longer be any problems with these names. Double sharp (talk) 14:01, 2 February 2015 (UTC)
- I notice that spherical polyhedron already mentioned the cases {1,1}, {2p,1}, and {1,2p} (though calling the last two {2p,2}/2 and {2,2p}/2). It uses the names "hemi-dihedron" for {2p,1} and "hemi-hosohedron" for {1,2p}. I guess they can be considered cited, albeit at a slight stretch (both elements of the words are attested with the right meanings, but I can't find them used together to create this compound). Double sharp (talk) 08:20, 1 February 2015 (UTC)
- In general they cannot exist for odd q. You cannot draw n lines right through a point but with an odd number of segment ends meeting. Nor can you cut a polygon from inside a sheet of paper and end up with an odd number of cut sides when you add the sides of the polygon to the sides of the hole. Those are good names, it would be nice if they could be reliably sourced. — Cheers, Steelpillow (Talk) 12:14, 31 January 2015 (UTC)
- OK, I think I see what you're describing. Can {1,q} and {q,1} exist for odd q? (I guess hemihosohedra and hemidihedra seem like reasonable terms, given the projective polyhedra like hemi-cubes.) Double sharp (talk) 06:00, 29 January 2015 (UTC)
- (All off-topic) I would call them hemishosohedra and hemidihedra. A hemidihedron has q edges, but its face has 2q edges. It is dodgy regarding such things as polyhedra, but they are perfectly respectable regular maps. Maproom (talk) 12:56, 28 January 2015 (UTC)
- {1,2q} may be constructed on the projective plane, where it is simply q lines through a point. I suppose one could call them projective hosohedra. The dual {2q,1} projective monohedron would be a single 2q-gon wrapped around a line subdivided into q segments. At this point, the wise among us begin to think, "hang on, do I have q or 2q edges here? I need to understand this kind of thing before I decide what is or is not a valid, or even degenerate, polytope". — Cheers, Steelpillow (Talk) 11:02, 28 January 2015 (UTC)
- I think Tom's analysis is correct. Like the octahedron, dihedra have both regular and quasiregular colorings. I'd go further and suggest that even-numbered hosohedra do as well (depending on your definition of quasiregularity). But I'll bet you won't find any of that in any reliable source. The hosohedra degenerate to infinite prisms in Euclidean space, but these are not the same structures as the prism polyhedra. — Cheers, Steelpillow (Talk) 07:28, 28 January 2015 (UTC)
- ^ Séquin, Carlo. "Symmetrical immersions of low-genus non-orientable regular maps" (PDF). Berkeley University.
To get to a quasiregular even-sided hosohedron, t{p,2}, ![]()
![]()
![]()
![]()
![]() , I think if you have to look at Norman Johnson's unpublished opinion, i.e. a hosohedron is more like a polygon, (t{p},
, I think if you have to look at Norman Johnson's unpublished opinion, i.e. a hosohedron is more like a polygon, (t{p}, ![]()
![]()
![]() ) than a polyhedron. Tom Ruen (talk) 18:47, 28 January 2015 (UTC)
) than a polyhedron. Tom Ruen (talk) 18:47, 28 January 2015 (UTC)
A recursive definition of quasi-regular, which agrees with how the term is used by Coxeter, is as follows:
- A polygon is quasi-regular if its symmetry group is transitive on the vertices. [regular
and truncated
]
- An n-polytope (n > 2) is quasi-regular if its symmetry group is transitive on the vertices and its vertex figures are quasi-regular.
Rectified polyhedra [1-ring Coxeter diagram] are quasi-regular, but so are the ditrigonary polyhedra, which are not obtained by rectification. For n > 3, rectified regular n-polytopes are generally not quasi-regular.
- p.s. This is the only paper [4] that I've found on "quasiregular polygons", but also "quasiregular prisms"(!?). Tom Ruen (talk) 19:09, 28 January 2015 (UTC)
- Looks like they're using "quasiregular polygon" to mean a polygon which is isogonal but not isotoxal. Thus the polygons at User:Tomruen/Truncated polygons should all qualify (although I'm uncertain on whether the authors are considering nonconvex polygons). The "quasiregular prisms" appear simply to be just prisms built on such polygons. Double sharp (talk) 06:08, 29 January 2015 (UTC)
- Glad to see there's been response here, but I don't think anybody has actually discussed the object I described, which I'll call a "hosodihedron" by analogy with "cuboctahedron" and "icosadodecahedron". It's a "flat prism" -- it has two n-gonal faces, but unlike a dihedron (which connects the two n-gons to each other) or a true prism (which puts n squares between them), they're connected by a ring of digons. Joule36e5 (talk) 03:43, 29 January 2015 (UTC)
- Are we still talking about spherical polyhedra? In that case, don't the digons in the ring have to be degenerate because their vertices aren't antipodal? Then r{n,2} (=r{2,n}) would look exactly like the dihedron {n,2}, except that the edges shared by the two faces are actually all digons with zero area. Incidentally, wouldn't this mean that the vertex configuration "2.2.2.2" could refer to either r{2,2} or {2,4}? The second is regular, but the first is only quasiregular. This seems surprising. Double sharp (talk) 06:00, 29 January 2015 (UTC)
- Yes, it's degenerate even on the sphere -- "doubly degenerate" in Euclidean space, perhaps as a consequence of it being the intersection of two (dual) degenerate cases. As for the 2.2.2.2 question, it seems to me that r{2,2} is identical to {2,4}, just like r{3,3} is identical to {3,4} -- the only distinction is if you choose to 2-color it, no? Joule36e5 (talk) 01:11, 30 January 2015 (UTC)
- NOTE: r{2,2}=={2,2} (


 =
= 



 ), but I suppose it depends on how you define operations on orthogonal mirrors. You could say rr{2,2}=r{21,1}=={4,2}, that is r{21,1}= =
), but I suppose it depends on how you define operations on orthogonal mirrors. You could say rr{2,2}=r{21,1}=={4,2}, that is r{21,1}= = 

 =
= 

 =
= 


 =
= 



 =
= 



 = {4,2}, but not {2,4}. Tom Ruen (talk) 04:31, 30 January 2015 (UTC)
= {4,2}, but not {2,4}. Tom Ruen (talk) 04:31, 30 January 2015 (UTC)
- I guess topologically speaking, r{2,2} and {2,4} are the same thing: but they'd get realized differently if you interpret r{2,2} as meaning a literal geometric rectification of the spherical improper polyhedron {2,2}. {2,4} would have all four digon faces have nonzero area, whereas r{2,2} would have them alternate between nonzero- and zero-area digons. Double sharp (talk) 08:11, 31 January 2015 (UTC)
- NOTE: r{2,2}=={2,2} (
- Yes, it's degenerate even on the sphere -- "doubly degenerate" in Euclidean space, perhaps as a consequence of it being the intersection of two (dual) degenerate cases. As for the 2.2.2.2 question, it seems to me that r{2,2} is identical to {2,4}, just like r{3,3} is identical to {3,4} -- the only distinction is if you choose to 2-color it, no? Joule36e5 (talk) 01:11, 30 January 2015 (UTC)
- I understand now what you are describing. I once searched for a term for those things, and failed to find one. I started using the word "lucanihedron" (from Greek λουκάνικο) because they remind me of strings of sausages. Maproom (talk) 09:14, 29 January 2015 (UTC)
- Are we still talking about spherical polyhedra? In that case, don't the digons in the ring have to be degenerate because their vertices aren't antipodal? Then r{n,2} (=r{2,n}) would look exactly like the dihedron {n,2}, except that the edges shared by the two faces are actually all digons with zero area. Incidentally, wouldn't this mean that the vertex configuration "2.2.2.2" could refer to either r{2,2} or {2,4}? The second is regular, but the first is only quasiregular. This seems surprising. Double sharp (talk) 06:00, 29 January 2015 (UTC)
- If you take (almost) any regular polyhedron and expand each edge into a digon, you will obtain a figure that is technically quasiregular but also degenerate. The regular hosohedra are exceptions because of course it simply creates a new hosohedron with double the number of faces. To my knowledge, none of these degenerate figures has a name because none is of any mathematical or physical significance. — Cheers, Steelpillow (Talk) 10:18, 29 January 2015 (UTC)
- Fair enough. My only reason for considering this to be a special case was because it's the intersection of a regular polyhedron and its dual, which is not true for the general case. But I'm willing to accept "nobody cares enough". Joule36e5 (talk) 01:11, 30 January 2015 (UTC)
- The cuboctahedron is the intersection of a cube with its dual octahedron, when reciprocated about a common midsphere. Ditto the icisidodecahedron, etc. — Cheers, Steelpillow (Talk) 08:48, 30 January 2015 (UTC)
- Most of the article is about quasiregular figures that can be formed by rectification of regular figures. These seem to be what Joule36e5 regards as a "special case", though I would have taken it to be the definition. Maproom (talk) 09:03, 30 January 2015 (UTC)
- But the three ditrigonal polyhedra cannot be formed this way, unlike the other examples, because none of p, q, r for them is 2.
- Isn't the way the regular polyhedra get constructed by the Wythoff construction creating them as quasiregular polyhedra anyway? Their vertex configurations don't come out as pq; they come out as (p.2)q, with degenerate digons. Of course you can then take away the digons and get a figure which looks the same but is now regular. (As Steelpillow mentions, the hosohedra are exceptions, though the dihedra are not. I wonder if this works for the strange cases where p or q is 1.) Double sharp (talk) 08:15, 31 January 2015 (UTC)
- Sorry, which are the three ditrigonal polyhedra? Once a polyhedron cannot be drawn on a sphere, the kaleidoscope model needs applying with caution. For example Coxeter's construction of his uniform hemi polyhedra on the sphere is a bit of a cheat. He ends up with diametral polygons which he arbitrarily treats as cutting across the sphere rather than lying on its surface. This cheat is entirely unjustified by the kaleidoscope itself. More significantly, a kaleidoscope of mirrors constructed in the projective plane will yield hemi polyhedra, while toroidal and hyperbolic kaleidoscopes are a law unto themselves. In fact, the uniform hemi polyhdra are more properly constructed from these projective and toroidal kaleidoscopes. — Cheers, Steelpillow (Talk) 12:14, 31 January 2015 (UTC)
- The three ditrigonal polyhedra are the small ditrigonal icosidodecahedron (
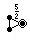 , χ = −8), the ditrigonal dodecadodecahedron (
, χ = −8), the ditrigonal dodecadodecahedron ( , χ = −16), and the great ditrigonal icosidodecahedron (
, χ = −16), and the great ditrigonal icosidodecahedron ( , χ = −8). Those Euler characteristic values do appear to suggest that I ought to apply some caution.
, χ = −8). Those Euler characteristic values do appear to suggest that I ought to apply some caution. - (On the other hand, the small stellated dodecahedron and great dodecahedron have χ = −6, and yet Kepler–Poinsot polyhedron still successfully shows them as spherical tilings. I assume this is because they cover the sphere multiple times? If so, should they really be thought of as coming from non-spherical kaleidoscopes?) Double sharp (talk) 12:45, 31 January 2015 (UTC)
- Yes, the ditrigonal stars are quasiregular but must be obtained through a different construction. Not even a "hemi" style cheat can save it. And like those two regular stars they are toroids. Any toroid which covers the sphere must do so multiple times. One may generate those that yield spherical symmetries from their Schwarz triangles on the sphere, but many do not yield such symmetries. All, whether constructible on the sphere or no, can be derived from their topological surface's "native" kaleidoscopes. A suitable metric can be defined within the surface to render them geometrically quasiregular as well as structurally so, but when injected into Euclidean space they will not necessarily "look" symmetrical. — Cheers, Steelpillow (Talk) 18:31, 2 February 2015 (UTC)
- So you can have star polyhedra which are actually topologically spheres (e.g. great stellated dodecahedron, great icosahedron) and star polyhedra which are topologically something else (e.g. small stellated dodecahedron, great dodecahedron). Cool! How do these native toroidal/projective/hyperbolic kaleidoscopes look like, say for simple-ish examples like the hemis, ditrigonals, or those two Kepler–Poinsots? I understand that they would probably be constructed the same way, by taking a fundamental domain and reflecting it across its edges, but I'm wondering how to better visualize the resulting tiling. Double sharp (talk) 14:17, 4 February 2015 (UTC)
- Yes, the ditrigonal stars are quasiregular but must be obtained through a different construction. Not even a "hemi" style cheat can save it. And like those two regular stars they are toroids. Any toroid which covers the sphere must do so multiple times. One may generate those that yield spherical symmetries from their Schwarz triangles on the sphere, but many do not yield such symmetries. All, whether constructible on the sphere or no, can be derived from their topological surface's "native" kaleidoscopes. A suitable metric can be defined within the surface to render them geometrically quasiregular as well as structurally so, but when injected into Euclidean space they will not necessarily "look" symmetrical. — Cheers, Steelpillow (Talk) 18:31, 2 February 2015 (UTC)
- The three ditrigonal polyhedra are the small ditrigonal icosidodecahedron (
- Sorry, which are the three ditrigonal polyhedra? Once a polyhedron cannot be drawn on a sphere, the kaleidoscope model needs applying with caution. For example Coxeter's construction of his uniform hemi polyhedra on the sphere is a bit of a cheat. He ends up with diametral polygons which he arbitrarily treats as cutting across the sphere rather than lying on its surface. This cheat is entirely unjustified by the kaleidoscope itself. More significantly, a kaleidoscope of mirrors constructed in the projective plane will yield hemi polyhedra, while toroidal and hyperbolic kaleidoscopes are a law unto themselves. In fact, the uniform hemi polyhdra are more properly constructed from these projective and toroidal kaleidoscopes. — Cheers, Steelpillow (Talk) 12:14, 31 January 2015 (UTC)
- Most of the article is about quasiregular figures that can be formed by rectification of regular figures. These seem to be what Joule36e5 regards as a "special case", though I would have taken it to be the definition. Maproom (talk) 09:03, 30 January 2015 (UTC)
- The cuboctahedron is the intersection of a cube with its dual octahedron, when reciprocated about a common midsphere. Ditto the icisidodecahedron, etc. — Cheers, Steelpillow (Talk) 08:48, 30 January 2015 (UTC)
- Fair enough. My only reason for considering this to be a special case was because it's the intersection of a regular polyhedron and its dual, which is not true for the general case. But I'm willing to accept "nobody cares enough". Joule36e5 (talk) 01:11, 30 January 2015 (UTC)
- If you take (almost) any regular polyhedron and expand each edge into a digon, you will obtain a figure that is technically quasiregular but also degenerate. The regular hosohedra are exceptions because of course it simply creates a new hosohedron with double the number of faces. To my knowledge, none of these degenerate figures has a name because none is of any mathematical or physical significance. — Cheers, Steelpillow (Talk) 10:18, 29 January 2015 (UTC)
missing
[edit]
(p.q)³ where p≠q, starting with (3.4)³. —Tamfang (talk) 20:30, 13 June 2016 (UTC)
- I see. I added row cases for (p p 3) and (p p 4) triangles. Tom Ruen (talk) 03:01, 14 June 2016 (UTC)
The definition from Coxeter et al.'s paper on uniform polyhedra (1954)
[edit]"Let us define a quasi-regular polyhedron as consisting of regular polygons of two kinds, say {q}'s and {r}'s, each entirely surrounded by specimens of the other kind (Coxeter & Whitrow 1950, p. 422)." He considers under this section 7 every uniform polyhedron of Wythoff symbol type p | q r that is not actually regular, and actually considers the hemipolyhedra q' q | r to be further quasiregular polyhedra on p. 417. This means that the hemipolyhedra should be reinstated as quasiregular in the article, as the section on star forms cites this very paper. Since later it is written "If r = 2 or r = q, the polyhedron p | q r is not only quasi-regular but regular (as we saw in §3)", we must conclude that Coxeter is considering the regular polyhedra to also be quasiregular by insertion of degenerate digon faces. Double sharp (talk) 15:47, 17 September 2018 (UTC)
- I have added the hemipolyhedra back to the article. For reference, the quote from the paper is "In this manner the octahedron {3
3} yields the tetratrihedron 3/2 3 | 2, and the quasi-regular polyhedra of §§1 and 5 yield further quasi-regular polyhedra as follows: {3
4}, 3/2 3 | 3 and 4/3 3 | 3; {3
5}, 3/2 3 | 5 and 5/4 5 | 5; {5/2
5}, 5/3 5/2 | 3 and 5/4 5 | 3; {5/2
3}, 3/2 3 | 5/3 and 5/2 5/3 | 5/3." While it is true that the tetrahemihexahedron is thus not explicitly called quasiregular, I believe we can plead common sense here, given that it is grouped together with the other eight hemipolyhedra and satisfies the definition given above just like the others do. - Incidentally, this implies that the hemi Euclidean tilings 4/3 4 | ∞, 3/2 3 | ∞, 6/5 6 | ∞, and 3/2 | 3 ∞ enumerated in the same paper should also count as quasiregular; they meet the definition just as well. Double sharp (talk) 14:27, 19 September 2018 (UTC)
- Added those tilings. Double sharp (talk) 14:38, 19 September 2018 (UTC)








