Talk:Poynting vector/Archive 1

Archive 1

Archive 2

Archive 3

Definition

Is the definition

S = E x H

or is it the complex conjugate of H

S = E x H*

Anyone know which it is? --H2g2bob 21:58, 23 May 2006 (UTC)

In nonquantum physics (which is what we are talking about here), the directional components of E and H are real numbers. So H=H* for any actual physical field. However, it is common in electrical engineering to apply a complex Fourier decomposition to the real fields and talk about complex valued sinusoidal waves. So the equations are modified to a complex form for handling such waves. JRSpriggs 03:45, 24 May 2006 (UTC)

The poynting vector is ExH which gives the instantaneous energy flow crossing unit area normal to the direction of flow per unit time. However, you may have seen ExH* in the expression for the time averaged poynting vector which is 1/2 Re(ExH*) and is the average energy of the electromagnetic wave crossing unit area (perpendicular to the vector) per unit time. —Preceding unsigned comment added by 62.31.207.26 (talk) 20:01, 6 May 2008 (UTC)

I believe this would be a nice addition to the article. It already says something about the time averaged poynting vector, but not as clear as here IMHO. Aphexer (talk) 09:19, 18 May 2009 (UTC)

Non-zero Poynting vector in static situtation

Let's imagine a simple situation: We have two vertical parallel metallic plates, carrying charges +Q and -Q, generating a homogeneous electrical field E. From above on a thin cord we hang between these plates a bar magnet, which eventually gets to rest. So nothing moves, nothing happens. Because there are electric and magnetic fields present, we can assign to any point in space a Poynting vector, which says, that at (almost) each point there is flowing energy.

I have difficulty to imagine and believe this. Is there any experimental evidence about this energy flow? Has it been measured? Please don't come with explanations from quantum physics. The Poynting vector was introduced in classical times in the end of nineteenth century. —Preceding unsigned comment added by Pschultz (talk • contribs)

Just because there is no radiation does not mean that there should be no linear momentum in the electromagnetic field, even if it adds up to zero. It may be necessary to store angular momentum. JRSpriggs 06:40, 7 September 2006 (UTC)

The energy can be considered to be circulating in closed loops. The electric and magnetic field exist also outside the plates. The energy can be considered to be continually circulating between the outside of the plates and the space in between them. However the net transfer of energy between any two points is zero. A better explanation is given briefly in Richard Feynman's "Lectures in Physics" volume 2 page 27-8. Grottlu 16:56, 29 December 2006 (UTC)grottlu

Another useful reference is Examples of Momentum Distributions in the Electromagnetic field and in Matter by W. H. Furry, published in American Journal of Physics 37, June 1969. A couple of quotes from this paper:

"Some recent papers [1-3] in this Journal have emphasised the importance of accepting the Poynting vector as a description of the space distribution of energy flux and momentum density in the electromagnetic field. As these authors have remarked, the deprecatory attitude toward the Poynting vector traditionally taken in textbooks is not only unfortunately misleading, but actually entirely incorrect. The example of angular momentum in a static field given by Pugh and Pugh [2] is particularly conclusive evidence for this."

"The idea that the Poynting vector is not to be taken seriously as a detailed distribution of energy flow and momentum density is a relic from the time when the energy-balance theorem for the electromagnetic field was taken as an isolated result. The single theorem indeed remains valid if one changes the Poynting vector by adding to it any vector whose divergence is zero. Such a change is clearly forbidden, however, by the theorems for momentum and angular momentum. The example given by Pugh and Pugh [2] conclusively vindicates the Poynting vector for the notorious case of a charged magnet for which generations of textbook writers declared that there could obviously be no actual energy flow."

The references [1-3] are [1] R. H. Romer, Amer. J. Phys. 34, 772 (1966); 35, 445 (1967); [2] E. M. Pugh and G. H. Pugh, Amer. J. Phys. 35, 153 (1967); [3] M. G. Calkin, Amer. J. Phys. 34, 921 (1966). A description of the Pugh & Pugh example can also be found in Albert Shadowitz's book The Electomagnetic Field (pp 426-429 in the 1988 Dover edition) and is interesting in that it describes a case where the discrepancy in mechanical angular momentum is exactly matched by the angular momentum of the static electromagnetic field. The angular momentum of the em field depends on the Poynting vector, showing the profound importance of this vector, even in the static case.AQv (talk) 17:26, 14 January 2008 (UTC)

I believe there is something in Feynman about this, which I am afraid I remember only very dimly. Imagine the parallel plates with the magnet dangling within. Start with no E-field between the plates, but the magnet suspended. Now apply the E-field (as gradually as you like). This is a changing E-field, so there must be a B-field circulating between the plates during this process. As the full charge is achieved this fades away again, but during the process it has imparted angular momementum onto the magnet. If you hold the magnet fixed w.r.t. plates, this momentum can only go into the fields? This is probably the Pugh & Pugh argument again? Perhaps you are free to choose a background divergence-free component at will, but you must be consistent between the start and end of the charging process - so if you assume no circulating energy before charging the plates, there must be circulating energy after charging the plates (which is equivalent to angular momentum?) Alas I don't own that particular volume of Feynman's lectures in physics (vol 2) but a quick search suggests Vol 2 chapter 27 MarkTillotson (talk) 21:04, 29 August 2008 (UTC)

I happen to have my copy of Feynman's Lectures on Physics opened to what you're talking about. Feynman's example is this: take a coil of superconducting wire with a current flowing through it and place it on a (frictionless) turntable. Then distribute charges around the rim of the turntable (say in the form of metal spheres). Finally, allow the superconducting coil to warm up until its temperature exceeds the critical temperature necessary for superconductivity. At first, this seems to pose a paradox: as the current in the coil dies, the magnetic field within the coil also dies; according to Maxwell's equations, this should create an electric field around the coil. The interaction of the electric field with the charges should push them, causing the table to start turning. On the other hand, the system began with no angular momentum, so it can't possibly begin to turn. However, if you analyze the Poynting vector while the magnetic field is still on, you'll see that it circulates around the turntable; thus there is a flow of energy, and consequently momentum, around the table. When the magnetic field dies, the momentum stored in the electric and magnetic fields becomes mechanical momentum in the turning of the table. (From The Feynman Lectures on Physics Volume II, 17-4 and 27-6) —Preceding unsigned comment added by Sebbie88 (talk • contribs) 18:15, 4 September 2008 (UTC)

One aspect that has not really been discussed, it seems to me, is the issue of what we mean when we say "energy flowing." I would like to point out a very interesting discussion of this concept in the book "The Classical Electromagnetic Field" by Leonard Eyges, Dover, 1972, on pp. 199-203. Eyges argues that the concept of where energy is stored is nebulous. He gives the example of a spherical shell of uniform surface charge density. There are two alternative formulas in classical electrostatics for finding the stored energy. One involves integrating the square of the electric field magnitude, and the other involves integrating the charge density times the potential. The first formula seems to imply that the energy is stored in all of space outside the shell, since this is where the electric field is. The second formula implies that the energy is stored only on the shell itself, since this is where the charge density is. Now, of course both formulas must give the same result when we integrate over all of space, and include all charges and fields, and this is easily verified. But we run into problems when we ask “where exactly is the energy stored?” The two formulas imply something quite different. Now, to quote Eyges, "But since one cannot identify the electromagnetic energy stored in a volume, one can scarcely verify that this same energy has moved someplace else. From this viewpoint, the concept of flow of electromagnetic energy is a tenuous one." We always get the correct answer for the total power crossing a closed surface when we integrate the Poynting vector over the surface. This power is what can be measured. However, in general, we cannot measure power crossing through an open surface (such as a loop). Indeed, how do we even define it? It seems to me that the concept of "flow" is one that involves some type of particles that are moving, like water molecules flowing in a river. We can count the number of water molecules crossing a given surface in a given amount of time, even if the surface is open (e.g., a small loop). But working only with fields, how do we define energy crossing an open surface?

Now, it is true that as we go to higher frequencies the electromagnetic field becomes more particle-like in character. For example, at optical or x-ray frequencies, it is convenient to talk about the energy flow in terms of photons. I think that here it does make sense to talk about energy crossing an open surface, since we can in principle count the photons. Hopefully any such experiment will verify the correctness of energy flow as given by the usual Poynting vector (as opposed to one where a curl term has been added). But at lower frequencies, where the dimensions of the open surface are not large compared with a wavelength, how can we measure, or even define, the energy crossing it? If we cannot do this, then it seems as if the question of whether the Poynting vector represents local energy flow in these cases is mainly a philosophical one. I invite comments on this. Elee1l5 (talk) 01:03, 9 October 2008 (UTC)

The angular momentum of the energy flux represented by the Poynting vector seems to be necessary for the general preservation of angular momentum. This is at least a strong indication that the energ flux should be interpreted as real, even for independent static E and B fields at an angle to each other. There are plenty of papers published dealing with the angular momentum of such static fields, so it's quite a well established idea. See earlier in this section. AQv (talk) 15:59, 20 January 2009 (UTC)

Having read the above comments, and the article I propose that the section "Independent E and B fields" should be rewritten, to reflect the consensus that the Poynting vector does indicate local energy flow, or at least the phrase "seemingly absurd" removed. I'm happy to contribute this, but don't wish to step on anyone's toes. Comments? Australisergosum (talk) 10:34, 8 June 2009 (UTC)

Poynting vector around a wire

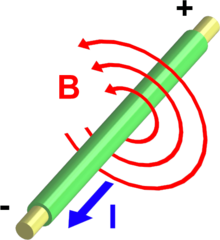
I removed this statement, but it was reverted: For example, the Poynting vector near an ideally conducting wire is parallel to the wire axis - so electric energy is flowing in space outside of the wire. The Poynting vector becomes tilted toward wire for a resistive wire, indicating that energy flows from the e/m field into the wire, producing resistive Joule heating in the wire. In an ideally conducting straight wire, there is no potential difference along the wire since otherwise the current would be infinite. That is simply Ohm's law. Hence, the Poynting vector ExH must be zero. If the wire has an ohmic resistance, E is parallel to the wire and H is circular around the wire. In this case, S=ExH will point into the wire, rather than being tilted towards the wire. I checked Jackson, Classical electrodynamics, 2nd edition, and it appears that more is wrong in this article. In the discussion of the Poynting vector, it states:

${\frac {\partial u}{\partial t}}+\mathbf {\nabla } \cdot \mathbf {S} =-\mathbf {J} \cdot \mathbf {E}$

(warning: Gaussian/CGS units; u is the electromagnetic energy density) and "Since only the divergence appears in the conservation law, the Poynting vector is arbitrary to the extent that the curl of any vector field can be added to it." Hence, it is not generally correct at all to interpret the Poynting vector as an energy flow per se. Furthermore, this was removed for "being untrue": For an electromagnetic wave propagating in vacuum, the irradiance can be written as

$I={\frac {1}{\mu _{0}c}}E^{2}={\frac {\epsilon _{0}c}{2}}E^{2},$

where E is the amplitude of the electric field, $\epsilon _{0}$ is the permittivity of free space.. For this I can simply refer you to Jackson, equation 7.13. Han-Kwang 07:58, 8 July 2007 (UTC)

What do you mean CGS? That's the way Poynting's theorem looks in SI units. AQv (talk) 15:55, 16 January 2008 (UTC)

You say you're quoting from the 2nd edition of Jackson's Classical electrodynamics. It was publised in 1975, but do you know that there is a third edition, from 1998? I haven't got access to it myself right now, but have you checked if the formulation about the arbitrariness of the Poynting vector is the same in this later edition? AQv (talk) 17:53, 16 January 2008 (UTC)

Given the price and how rarely I look up things I never bothered buying the new edition. I'll see tomorrow if someone at work (a physics research lab) has the new edition. Han-Kwang (t) 18:33, 16 January 2008 (UTC)

Explanation of revert by JRSpriggs

(1) You dropped a factor of two in your irradiance equation, since $\mu _{0}\epsilon _{0}c^{2}=1\!$ is an identity.

(2) You said "In an ideally conducting straight wire, there is no potential difference along the wire since otherwise the current would be infinite. That is simply Ohm's law. Hence, the Poynting vector ExH must be zero.". This is false and shows that you do not know what you are talking about. The E field would not be along the wire, it is perpendicular to the wire (pointing away from it or towards it). Since the B field wraps around the wire, the S which is their cross product points along the wire. How else could the electrical energy from the source be delivered to the load?

(3) Also your statement about S being indeterminate by a constant is false. S represents the flux of energy (or density of linear momentum) and is part of the stress-energy tensor which is the source of the gravitational field. Consequently, it must have a definite value at each event in space-time.

(4) There is no basis for introducing square-roots where you introduced them.

I will not waste my time looking for additional errors. These are enough to justify reverting you. JRSpriggs 02:28, 9 July 2007 (UTC)

Han-Kwang's rebuttal

I based most of my edits on Jackson's Classical Electrodynamics. If you doubt the validity of this standard reference, you should provide a reference.

(1) Agreed, thank you for pointing this out to me.

(2) The E field would not be along the wire, it is perpendicular to the wire (pointing away from it or towards it). -- The current in an ohmic wire follows the eq. J = sigma E, which means that the field in general is along the wire. However, I think I see now what you mean. Since in a typical application, there is another wire somewhere else at a different potential, the is a field perpendicular to the wire. However, this is not generally the case, so such a statement should be clarified. For example, there is no potential difference with a superconducting loop in a magnet. In any case, the current article statement Poynting vector becomes tilted toward wire for a resistive wire, indicating that energy flows from the e/m field into the wire, producing resistive Joule heating in the wire. is misleading, since the Poynting vector should be used in Poynting's theorem, in conjunction with the energy density u and the current dissipation J.E.

(3) Quoting from Jackson page 237: The vector S, representing energy flow is called the Poynting vector. It is given by S=c/4pi (ExH) [CGS units] and has the dimensions of (energy/area x time). Since only its divergence appears in the conservation law, the Poynting vector is arbitrary to the extent that the curl of any vector field can be added to it. Such an added term can, however, have no physical consequences. Hence it is customary to make the specific choice (eq 6.109).

(4) I am not sure what you mean. Do you mean this one?

$\langle S\rangle ={\frac {1}{2\mu _{0}c}}{\sqrt {\frac {\epsilon _{r}}{\mu _{r}}}}E_{0}^{2}$

It is based on the CGS equation 7.13 in Jackson: S = c/8pi * sqrt(epsilon/mu) * |E0^2| * n, where n is the unit vector in the direction of propagation. Did I make an error in the conversion into SI units?

Han-Kwang 06:50, 9 July 2007 (UTC)

Jackson's paper Surface charges on circuit wires and resistors play three roles, Am. J. Phys. 64(7), July 1996, pp 855-870, supports the idea of a perpendicular component of the electric field outside the wires of a circuit. It's caused by surfaces charges on the wire, not by a distant source. AQv (talk) 16:52, 4 January 2008 (UTC)

yes, but that is already discussed below. (whether you prefer to interpret the field as a result of surface charge or potential difference is a matter of taste, not something fundamentally different) Han-Kwang (t) 00:45, 7 January 2008 (UTC)

Wire discussion

I made the following diagram as an illustration to point (2).

Shown are a couple of ways to send current through a closed loop of wires, with the E, H, and S fields in blue, black, and red, respectively. I think it is clear that a statement along the lines of "the Poynting vector is parallel to the wire" is only correct in very specific cases. Han-Kwang 09:35, 10 July 2007 (UTC)

jrs to hw

(1) You are welcome.

(2) Do not forget that the context of my statement was that the wire was non-resistive. If it has resistance, then the Poynting vector will tilt towards the wire since it absorbs some of the power. It is true that I was assuming that the wire leads to a load which consumes most of the power. Your drawings are helpful in showing that the situation may be more complicated. If you want to add qualifications to the paragraph to make it correct, then go ahead. But I object to your statement that the vector was zero, which is also not true generally. Even if there is not a second wire, the current has to return through the chassis, Earth, water, air, or whatever. So an electric field will exist between the wire and that other conductor.

(3) Standard text or not, I think that Jackson is just wrong, if he says "Since only its divergence appears in the conservation law, the Poynting vector is arbitrary to the extent that the curl of any vector field can be added to it. Such an added term can, however, have no physical consequences.". The stress-energy tensor could not transform correctly under coordinate transformations as required by the theory of relativity, if the "added term" were present, nor could the Einstein field equation be satisfied. I have never seen any other text mention this alleged indeterminacy of the Poynting vector. And it would clearly be pointless to even look for a refutation of his statement, just as it would be pointless to look for a reference which said "The Poynting vector is not made of green cheese.".

(4) Yes, that is the equation I meant. I am not complaining about the units. I am concerned about how you justify the square-root. Please explain how you (or Jackson) derive that equation. JRSpriggs 05:37, 11 July 2007 (UTC)

HK's reply

I'm glad to see that we can have a reasonable discussion to improve the article.

(2) I guess it will be an diagram similar to the the middle diagram above. I'll be without internet for a while, so I will defer this to a couple of weeks from now, except of course if you feel like making better illustrative diagrams yourself.

(3) Special relativity is rather far away from my daily expertise. However, Jackson mentions the stress-energy tensor in section 12.16 and says that the "covariant generalization of the differential conservation law of [Poynting's theorem] is

$\partial _{\alpha }T^{\alpha \beta }=0\,$".

The tensor T contains lots of ExB terms, as well as an E^2+B^2 term (equivalent to u in Poynting's theorem). You probably know all this, but I'm trying to summarize what I understand from reading this. I'll assume that you're correct that replacing ExB by ExB+curl C (for any C) will result in an inconsistent stress tensor. However, I see no contradictions here, since Jackson writes the stress tensor components for example as (leaving out the 4pi factors)

$T^{0i}=(E\times B)+\nabla \cdot (A_{i}E)$

and not as

$T^{0i}=\mu S+\nabla \cdot (A_{i}E).$

Are there any authors who write the stress tensor as in the latter equation? In any case, there is no μ and/or H in the stress tensor either. I assume that special relativity (did you say gravitational field???) doesn't deal with macroscopic μ and ε parameters.

(4) Leaving out the cumbersome 4pi etc. prefactors and vectors,

$B_{0}={\sqrt {\mu \epsilon }}E_{0}$

$\langle S\rangle =E_{0}H_{0}/2=E_{0}(1/\mu )B_{0}/2={\sqrt {\epsilon /\mu }}E_{0}^{2}/2$

Han-Kwang 06:53, 11 July 2007 (UTC)

jrs to hk

(3) I did not mention "special"; I was referring to general relativity. The correct expression for the mixed time-space components of the electromagnetic stress-energy tensor in an inertial frame of reference is

$T^{0i}=T^{i0}=S_{i}={\frac {1}{\mu _{0}}}(E\times B)_{i}\!$

If you mean the A in $+\nabla \cdot (A_{i}E)$ to refer to the vector potential, then this would violate gauge invariance as well as having no justification that is apparent to me. JRSpriggs 03:44, 14 July 2007 (UTC)

hk to jrs

OK, general relativity is definitely outside my expertise, so I can't comment much on that. But I still would like to point out that the definition of the Poynting vector on electromagnetic stress-energy tensor (i.e. ExB/mu0) is different from that on this page (ExH). In a linear medium, the difference is $\mu _{r}$, with things like hysteresis it gets worse. It might be best if we explain in this article that there are different definitions of the Poynting vector, with slightly different properties, depending on which field within physics.

It could something along the lines of:

In classical electrodynamics, as described by Jackson, S=ExH; its definition is arbitary to the extent of that the curl of any field can be added to it. In general relativity, S=ExB/mu0. It appears in the e.m. stress-energy tensor and because of gauge invariance, the curl arbitrariness does not apply here.

Han-Kwang 14:01, 31 July 2007 (UTC)

Standard textbooks

Example of incorrect picture of the electromagnetic wave.

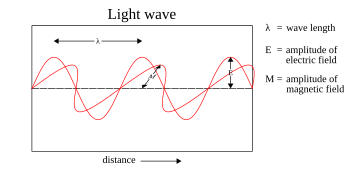
Standard textbooks sometimes does define Poynting vector as $\mathbf {S} =\mathbf {E} \times \mathbf {H}$, probably for sake of simplicity, or more probably for sake of tradition (just as they call H, not B, the magnetic field for sake of tradition). However, Poynting vector is $\mathbf {S} ={\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B}$ and magnetizing field is $\mathbf {H} ={\frac {\mathbf {B} }{\mu _{0}\mu _{r}}}$, which gives $\mathbf {S} =\mathbf {E} \times \mu _{r}\mathbf {H}$ if one wants to express the Poynting vector in terms of E and H.

One example to show that standard text books can indeed be colectively be wrong is the picture of electromagnetic wave in which magnetic and electric fields are in phase, which is incorrect, but it is unfortunately much more often used than correct picture.

If standard textbooks do some errors we don't have to blindly copy those errors. This is one of the many examples how obeying the tradition can be harmful. Thank you for understanding. --78.0.23.69 (talk) 16:52, 21 December 2007 (UTC)

E and B (or H) are in phase in a plane wave. What are you talking about? Han-Kwang (t) 00:40, 7 January 2008 (UTC)

Quite - just to explain this for 78.0.23.69, deriving the e-m plane-wave solution from Maxwell's equation involves relating the E-field to the B-field via (for instance) curl-of-E relates to time-differential-of-B. This relates the differential of one field w.r.t. space (curl) to the differential of the other w.r.t. time. so the phase difference is a multiple of 180 degrees, not 90. Its very informative to do this exercise for the plane-wave case as it explains e-m radiation, waveguides, relationship between $\mu _{0},\epsilon _{0}$ and c. MarkTillotson (talk) 21:23, 29 August 2008 (UTC)

A further point - perhaps there is confusion about circular polarisation (which is simply the superposition of linearly polarised plane waves) the E and B fields rotate 90 degrees apart in space... MarkTillotson (talk) 21:30, 29 August 2008 (UTC)

I wonder if the current definition in the article of the Poynting vector as S=Exμ_rH isn't wrong, and that S=(1/μ₀)ExB should be valid only for free space, while S=ExH covers both free space and cases with μ_r$\neq$ 1. According to Encyclopaedia Britannica's online article about the Poynting vector: "The Poynting vector S is defined as to be equal to the cross product S=(1/μ)ExB, where μ is the permeability of the medium through which the radiation passes", and I've never seen S=Exμ_rH anywhere in literature. AQv (talk) 17:37, 7 January 2008 (UTC)AQv (talk) 15:02, 8 January 2008 (UTC)

I suspected exactly the same thing (it was changed recently). According to Jackson (standard reference!), it's ExH, but according to Griffiths "Introduction to electrodynamics, 2nd ed.", it's ExB/mu0. It's also like that according to hyperphysics, but there free space is explicitly mentioned. The mu0 in Griffiths' version comes from Ampere's law, which is curl B = mu_0 J without a mu_r appearing. (It's like that on Wikipedia, in Griffiths, and Jackson after CGS->SI conversion). Anyway, since I have 2 references for mu0 and 1 reference for mu0*mur, and I don't feel like redoing the derivations myself, I decided to leave it as it is now. Han-Kwang (t) 17:58, 8 January 2008 (UTC)

I can think of two reasons why S=ExB/μ₀ is often found in textbooks. One is that free space is often assumed even when not explicitly stated. The other is that for many diamagnetic and paramagnetic substances μ_r is close enough to 1, making the free space approximation of S as ExB/μ₀ acceptable in these cases. (Being quite inexperienced as an editor I'd rather wait, too, before making any changes, at least until some consensus has been reached.) AQv (talk) 18:37, 8 January 2008 (UTC)

I've removed the mu_r from the definition and added a remark that it is for free space, such that it is certainly correct, although maybe incomplete. When we've sorted this out, we can add a version for materials with mu_r > 1. Han-Kwang (t) 23:50, 8 January 2008 (UTC)

At hyperphysics free space isn't even implicitly mentioned. Only thing that has to with free space mentioned there is sentence Electromagnetic waves carry energy as they travel through empty space. which only says that em waves doesn't need non-free space to propagate. --83.131.29.161 (talk) 09:36, 12 January 2008 (UTC)

Notice how c is used several times on that page. It stands for the speed of light in vacuum, and the way it is used shows that free space conditions are in fact implied. If you follow their link to speed of light, you'll notice that they say the speed of light is 299,792,458 m/s, forgetting to mention that this is the speed of light in vacuum only (which it obviously is). AQv (talk) 18:27, 14 January 2008 (UTC)

Free and non-free space

Perhaps this Jackson guy was having free space in mind when he said "S=ExH". --83.131.77.67 (talk) 13:50, 3 February 2008 (UTC)

May I suggest the following refereed scientific paper (my own): http://www.iop.org/EJ/abstract/0295-5075/81/6/67005 ? It deals with the proper derivation of the Poynting vector and Poyntings theorem and hopefully answers the questions posed in this section. If there are doubts, feel free to send an e-mail (address see paper). The paper is also freely available at http://arxiv.org/abs/0710.0515v3 The bottom line is that S=ExB/μ₀ is the proper Poynting vector and is valid everywhere (in vacuum as in matter), but ExH is only valid after some approximations are made. If the properties of the medium are described by simple constants like μ_r, the Poynting vector could be written as S=(1/μ)ExB=ExH but the consequence is that the electromagnetic energy density can no longer be given! 139.30.44.17 (talk) 17:05, 26 June 2008 (UTC)

Thanks! I quickly scanned through the article, but I'm not sure what these approximations are. The paper explicitly mentions spatial dispersion, but I'm not sure what that means. Maybe you can clarify that and also give some comments about other disagreements (e.g. whether adding an arbitrary rot X is allowed or not) here on this talk page? Han-Kwang (t) 17:40, 26 June 2008 (UTC)

You could add any vector rot X to S without altering the energy continuity equation (eq 1 in article). But this vector S'=S+rot X just would no longer be the pure energy flux vector. The article shows that S=1/μ_0(E x B) naturally evolves from the Maxwell-Lorentz equations in just two steps. Moreover, an additional rot X is not compatible with a relativistic formulation. This is dealt with in Jackson (4th ed.) also.

On spatial dispersion: The effect of the presence of a certain medium in an electromagnetic field E is given by the polarization field P, which superimposes E to the resulting field D. Now, let's imagine some very general relation for P. The field P at point r ant time t may depend on the electromagnetic field at a different point r' and different time t' (of course, t>t'). It may also depend on the strength of E in a non-proportional way, but then we have a non-linear medium, which is not dealt with in the article. So we have a factor between P and E that depends on where and when P is measured and, also, on E at a certain position and time. This factor contains all the information about the properties of the medium (and this is the only place where these properties enter). The field E at all times (t'<t) and all points in space may have an effect on P, so we have to integrate over r' and t'. The same applies for magnetic fields B and the magnetization M. This is exactly what equations (11) tell us, the factor I mentioned is the susceptibility chi (χ). This is the most general linear formulation, and the Poynting vector and Poynting's theorem as well are perfectly valid as shown.

We can now apply some approximations. First, we could say that the medium does not change over time. chi then depends only on the time difference (t-t'). We could also say, the medium is spatially homogeneous, i.e., it looks the same everywhere. chi then depends only on the spatial distance (r-r'). The crucial point is that this can only be true for an infinitely extended medium. The mere presence of a medium surface or boundary implies that chi is spatially INhomogeneous! A spatially inhomogeneous chi is equivalent to spatial dispersion. If we accept the assumption of an infinitely extended medium, we can approximate further and say that chi doesn't really depend on (r-r'), but only on the time difference (which is identical to a frequency dependence). We then have the well-known frequency dispersion which, e.g., causes the light to split up into the color spectrum in a prism. If we further deny the frequency dependence, we arrive at a simple constant chi, which can be re-written as ε_r or μ_r in the electric or magnetic case, respectively.

The message of the article is that if one starts his considerations at the end of this chain of approximations and tries to work his way up, something goes wrong and one will arrive at the questions posed here. If you start at the full material equations (11) together with the microscopic Maxwell-Lorentz equations, everything comes out fine.

Due to the historical situation, physicists were first interested in crystal optics. Here, all of the above approximations were viable and they considered at most a frequency dependence, focusing more on the geometry of the crystal lattice. This situation still is reflected in today's textbooks, where Maxwell's equations are often introduced with a constant chi (i.e., ε or μ) and the Poynting vector ambiguously as S=1/μ_0(E x B)=E x H. 139.30.44.17 (talk) 09:10, 27 June 2008 (UTC)

Thank you for your comments. Can I try to summarize the essential points?

1. S=ExH is not correct if ε_r or μ_r depend on the position (including boundaries from one medium to another)
2. S=ExH is not correct if ε_r or μ_r are frequency-dependent (that surprises me).
3. S=ExH is not correct if the medium has a nonlinear response.

I'd also like to hear your opinion on the application of the Poynting vector on non-radiative fields, such as the example of the coaxial cable (it gets worse if you put the ground point somewhere else, see my drawings elsewhere on this page) and the magnet with static charges. My opinion is that the Poynting vector only makes sense in the context of Poynting's theorem, and only for radiation it can be interpreted as an energy flux. Han-Kwang (t) 09:53, 27 June 2008 (UTC)

Let's see (correcting myself a little bit):

1) S=1/mu_0 (E x B) is always valid and purely radiative. You can clearly distinguish between radiative and mechanical energy flux, and corresponding potential energy densities can be given.

2) If there are no magnetic effects of the medium, S=1/mu_0 (E x B)= E x H.

3) You could formally define S'= E x H, but the downside is:

a) S' is not purely radiative, but also contains contributions from induced currents (i.e., mechanical energy from charged particle motion!) see eq. (2)

b) You cannot give a potential energy corresponding to this mixed energy flux S' unless you can strip down the full material equations (11) by approximations to something like eqs. (12), and ε_r and μ_r are really constants (not frequency dependend).

4) To be strict, such approximations can only be made for infinitely extended, linear media that do not change properties over time (steady state/equilibrium). 139.30.44.17 (talk) 16:58, 27 June 2008 (UTC)

Thank you again. I've tried to incorporate the essence of your comments into the article. I didn't use as much detail since there is a significant risk that I'll make errors and moreover it would require a substantial rearrangement of the article. Feel free to correct the article for any errors. Han-Kwang (t) 19:34, 27 June 2008 (UTC)

Well done, thanks. I finally decided to open an account and I concretized the problem one runs into with S= E x H. I think the article now covers the crucial point very well. Nebeleben (talk) 12:35, 29 June 2008 (UTC)

There is one simple example where S = E x H makes more sense as representing an energy flow than does S = 1/mu_0 (E x B): Consider a long straight cylindrical current-carrying conductor in a DC circuit. It can be shown that the net perpendicular energy flow (Poynting flow) into a cylindrical segment of the conductor is equal to the expected power dissipation P = IV. You can see this derivation done in section 4.5 of Ian M. Sefton's Understanding Electricity and Circuits:What the Text Books Don’t Tell You. He doesn't bother to include the weak magnetic properties of the wire or the surrounding media in that derivation, but let's consider the case of both the wire and the surrounding air having weak simple magnetic and dielectric properties characterized by scalar mu_r and epsilon_r, both of which may be different for the two media involved. As you will know, the parallel component of the electric field is is continuous at the boundary between the two media, even if epsilon_r isn't. Likewise, the parallel component of H is continuous at the boundary, even if mu_r isn't. The parallel component of B, on the other hand, is not continuous if mu_r isn't! This means that if S is defined as S=1/mu_0 (E x B), S will be discountinuous at the surface, implying that at the boundary energy is continuously either accumulated or depleted! This is not a fortunate physical situation, and I think this supports the idea that at least in this case, S = E x H gives a much more plausible definition of the Poynting vector, if we want this vector to represent an energy flow. (But, lacking a reliable reference, I'll wait before adding anything about it on the main page.) AQv (talk) 16:47, 21 July 2008 (UTC)

You have a good point. So Jackson was right after all. Apparently something happens when you make the transition from a steady-state case to propagating waves. Han-Kwang (t) 17:29, 21 July 2008 (UTC)

Remember that epsilon_r and mu_r are strictly valid only for infinetely extended media. You cannot expect them to produce correct results at a medium boundary. The total energy is conserved and the total Poynting vector is continuous, but if the model of the material is not good enough, it might produce a non-continuity in the electromagnetic Poynting vector and a second one in the mechanical Poynting vector, which compensates the first. So non-continuity might be an artefact of the model and is not a good point here. I hope I can come up with a more descent, "positive" explanation soon. -- Nebeleben (talk) 18:02, 27 July 2008 (UTC)

When you say that S=ExB/μ₀ is the "proper" Poynting vector, in vacuum as well as in matter, I wonder if you're not putting an old name on a new entity? Traditionally the Poynting vector is defined as S=ExH, and even if you and your colleagues find it very useful to work with S=ExB/μ₀, rather than S=ExH, in matter as well as in free space, I wonder if a new name shouldn't be invented for this new vector. Calling it the "proper" Poynting vector is very confusing, and I question using your paper as a reference for the actual definition of the Poynting vector. This is not meant as a critique of the paper, or even of including it in the reference list, but to let such a recent paper from 2008 overthrow the old established use of the name "Poynting vector" is questionable, even if the paper has been refereed. I can't see it as a valid reference for the definition of the Poynting vector.

About the discontinuity in mu_r, I'd say that even if the discontinuity in real materia isn't a proper mathematical discontinuity, but only a drastic but continuous change, it still raises the same question about a very high accumulation or depletion of energy in a very thin, even if not infinitely thin, layer of materia. AQv (talk) 16:00, 28 July 2008 (UTC)

I'm sure this is not the only case where a physical quantity or law has changed from its original form due to re-interpretation, the need for a consistent reformulation together with other laws or just the ongoing development of the theory. One example are Maxwell's equations.

We were not the first to call S=ExB/μ₀ a "Poynting vector", and I think we should continue to do so in honour of its inventor. Also, people have introduced "acoustic" Poynting vectors and such. Our paper does not try to define the Poynting vector, but shows differences and implications of the existing definitions, so please don't mistake its citation in the Wikipedia article as a pointer to the origin of the definition (it is - by far - not!, and Jackson's book isn't either). Maybe we could change the first paragraph of this article to something like "One practical definition of... though the original definition is..."?

I did call S=ExB/μ₀ the "proper" Poynting vector, and you are right, that's confusing, but please bear in mind, I did so only on this discussion page. "Proper" is meant in the sense of "as it was meant to be" (Have a look at the first sentence of Poynting's original article!) or "as it is widely understood", namely as the flux of radiative energy carried by the physical fields. Additionally, it seems very unfortunate to me to introduce a quantity that mixes such different things as field energy with certain parts of a current and to which no corresponding energy density can be given.

By the way, I do not understand your point in the comment above - Sefton uses S=ExB/μ₀ and finds the right energy dissipation, so what's wrong? -- Nebeleben (talk) 20:55, 28 July 2008 (UTC)

Reading this again with regard to the fact that we are dealing with an encyclopedic article rather than scientific research in general, I find that I didn't give satisfying answers to the questions you arose. I will have a look for a more original reference for the definition of the "proper" Poynting vector, but I suspect that this will be hard to find, even though it is used quite often. If this was only an academic idea without practical use, it shouldn't be mentioned in an encyclopedic article so prominently, so some reference would be nice to to have. On the other hand, for such a purely theoretical topic, it's hard to draw the line between "academic use" and "practical use". I wonder if these categories even apply... In a comment above you mentioned some textbooks which employ the "proper" definition yourself. Wouldn't a textbook reference be enough? -- Nebeleben (talk) 07:30, 29 July 2008 (UTC)

The reason the derivation in Sefton's text works for S=ExB/μ₀ is that he also uses B = μ₀I/(2πr). Had he used μ instead of μ₀ in this expression, he also would have needed to use S=ExH to make it work. AQv (talk) 16:14, 30 July 2008 (UTC)

I'm not sure what you mean by the first sentence of Poynting's original article, is it the introductory A space containing electric currents may be regarded as a field where energy is transformed at certain points into the electric and magnetic kinds by means of batteries, dynamos, thermoelectric actions, and so on, while in other parts of the field this energy is again transformed into heat, work done by electromagnetic forces, or any form of energy yielded by currents. from Poynting(1884) On the Transfer of Energy in the Electromagnetic Field?

The problem with identifying a term as the elctromagnetic energy flow S_e, as is done in eq. (6) in your paper, is that this by itself is not a proof that this vector actually represents the electromagnetic energy flow. (Feynman discusses this issue in relation the the derivation of the "classical" Poynting vector in chapter 27 of Feynman Lectures.) AQv (talk) 16:50, 30 July 2008 (UTC)

I'll be glad to explain further (as far as I can), perhaps we should continue that via email? You know where to find my address. Please have a look at the concept of total/free/bound charges/currents before. See, for example, Maxwell's equations.

Yes, I referred to the sentence you cited. Poynting aimed to separate energies into energies carried by the fields and energies such as heat and work, as far as I understand this (as a non-native speaker).

Briefly: 1) Heat is kinetic energy, and all particles contribute, so it's the total current that counts. Corresponding Maxwell's equation is $rotB=\mu _{0}j_{total}$ 2) If the kinetic energy of all particles is included by definition, what other kinds of energy besides field energy could be present? -- Nebeleben (talk) 20:54, 31 July 2008 (UTC)

(I'll start from the left margin again in order not to indent too much, and because the discussion is about a reference to the main page it's better, I think, to keep it open to anyone who wants to have a say.) How do you deal with magnetisation caused by orientation of electron spins? What j in $rotB=\mu _{0}j_{total}$ could be used to account for the magnetisation of for example molecular oxygen O2, which is paramagnetic due to two unpaired parallel electron spins in each molecule, and how does this relate to a kinetic energy density U_m or kinetic energy flux S_m? I don't quite see how the electron spins fit into your equation (3b).

The energy density given in your eq. (5) is similar to that normally given for free space only. Reitz, Milford & Christy's Foundations of Electromagnetic Theory, 3rd ed., gives a derivation of the energy density of a magnetic field in linear media as u = H•B/2 (in section 12-2) and the energy density of a electrostatic field in linear media as u = E•D/2 (in section 6-3). Are those derivations, in your opinion, wrong because they give a result different from yours (except in free space)?AQv (talk) 14:59, 1 August 2008 (UTC)

(I moved a few comments in order to put them in chronological order.) I understand that a current density j can be derived from rot M. But, since Maxwell's equations don't really deal with intrinsic spin of elementary particles, and perhaps not even really with the magnetic momentum derived from atomic electron orbitals, I fail to see how a bound j = rot M could be treated as a current with a given mechanical kinetic energy. From rot M you only get the current density j, but if you want to write j as qv, or as a sum over q_iv_i there's no way to find v or v_i from j, especially if M derives mainly from such things as electrons' intrinsic spin, or their atomic (or perhaps molecular) orbitals. In short: j derived from rot M seems to me to be a rather theoretical current, not necessarily having a well-defined mechanical kinetic energy like the expression in for example eq. (7) in your paper. So how do you then explain the discrepancy arising from the discontinuity of ExB at the boundary between two media? AQv (talk) 14:55, 5 August 2008 (UTC)

I would like to invite you again to continue this discussion by email - I do not see it attract much interest, it's getting lengthy and doesn't seem to find back to the main point soon, and last but not least, it's much easier for me. Of course we should leave a note here about the result.

Again, brief responses to your questions: 1) This is absolutely well-founded classical physics. $rotB=\mu _{0}j_{total}$ is just Maxwell's equation and we really should agree to trust it. Remember that spin is a quantum-mechanical phenomenon and we're here in a classical context. Eqs. (3a+b) are used in Claude Cohen-Tannoudji's introduction to QED as a starting point. This is also to say you needn't worry much about compatibility of the classical approach with a quantum-mechanical generalization if it's needed. Furthermore, since we never want to calculate S_e or U_e, we don't really need to know q and v, just in principle. Later, one may introduce averaged macroscopic quantities, and then we're back at D and H.

2) No, Reitz's result is not "wrong", it is just physically different (it includes the induced/bound current contributions and is thus not purely radiative), and, to my knowledge, it is only possible establishing these energy densities with some further assumptions, e.g., that the material equations can be written as in Eq. (12) in the paper. That's most certainly the reason why Landau/Lifshitz refrain from giving U and just mention the total differential, dU. If you add up a frequency-dependence in epsilon or mu, than things get already much more complicated (Re(d(mu omega)/d omega)). Nevertheless, this is still covered in Jackson's book. Have a look, he calls U in this case "effective" and also mentions clearly the approximations. Next step: Try to derive U from dU in the case of a spatially dispersive or even inhomogeneous medium and see how far you come. - Could you provide me with a copy of the relevant sections of this book? It'll take me a few weeks to get one otherwise, unfortunately. Then I could check whether their derivation manages to avoid this assumptions.

For the discontinuity of S, the same arguments as above still apply. -- Nebeleben (talk) 15:50, 5 August 2008 (UTC)

(On discontinuity, added later:) I'll try to put in other words: If one assumes a set of material equations, namely $B=\mu H,D=\epsilon E$, knowing that they are an approximation for infinitely extended media, and than looks for an energy flow expression that is continuous at a medium boundary, one puts the cart before the horse, and the horse suffers a serious colic.

Rather, since E and B are the physical fields (see Jackson), the continuity of these two fields is the physical condition that has to be fulfilled, and if there is a model or approximation that cannot be made consistent with this condition, it has to be deemed inappropriate and may not be used in studying the special case, even though it may give good results in other circumstances. In our case, the conflict is quite obvious: infinitely extended media don't have boundaries. Conclusion: The given form of the material equations will lead to wrong results.

What does the situation look like in the medium close to the boundary? Different from that in the middle of the medium, because the continuity of E and B implies that electromagnetic energy is transfered continuously into other kinds of energy, starting at zero at the medium boundary. So there is clearly a dependence on the position, which $B=\mu H,D=\epsilon E$ simply do not reflect. More general material equations that contain the necessary spatial dependence are shown in Maxwell's_equation#General_case (I have tried to describe them phenomenologically above). The continuity condition becomes then a condition for the formulation of the susceptibility, which has enough degrees of freedom to be able to fulfill it. We then have E, B continuous by definition and, automatically, $S_{e}=1/\mu _{0}(E\times B)$ as well as S_m, too, and there is no energy depletion at the surface whatsoever. Last but not least, we also have an exact, well-defined energy density U_e. Compare that with the many rough edges of the traditional definition, which I assume is a kind of historic burden (see above and in the paper). -- Nebeleben (talk) 08:38, 6 August 2008 (UTC)

Regarding interest here: I do watch this page because I am interested in whether it's ExH or ExB/mu0. I admit that I am not trying to follow the whole discussion in detail, though, and maybe a specific discussion which is not related to improving the article is better conducted over email. I think for the time being, it may be better to revert to S=ExH (as is standard in text books) with a note that in some applications, ExB/mu0 may be a more appropriate definition.Han-Kwang (t) 16:02, 5 August 2008 (UTC)

Let's just agree to disagree then. I'm afraid I can't really believe in your paper, and it would only be a waste of your time trying to convince me further at this moment. AQv (talk) 12:05, 6 August 2008 (UTC)

I have restored the ExH definition, but kept the ExB/mu0 as an alternative expression. Regarding the example of the singularity in a coaxial cable filled with a dielectric that has a discontinuity in mu_r, I suspect the problem is in reflections. If you consider a DC current, you need continuity in H and hence ExH is a proper definition. However, if you consider a wave travelling through the coaxial cable, there will be a reflection and it wouldn't surprise me if the H component due to the reflected wave exactly accounts for the discontinuity in H that you would have in the absence of reflection when using the ExB definition.

On the other hand, in the derivation of Poynting's theorem on Wikipedia, the definition ExB/mu0 is assumed. I think the current article text is reasonable in that it presents the traditional definition first, even though it may or may not be correct in specific cases, and makes a remark about special cases. Han-Kwang (t) 14:33, 6 August 2008 (UTC)

That's all fine for me, I suggested something similar above. This discussion was more scientific then about the right wording for an encyclopedia. However, I think that even in a Wikipedia article, the equations shouldn't be given in a form where certain approximations have been applied and which have been simplified afterwards. That is, let's write them in terms of E,B,D,H,P and M (not eps_r, mu_r) and add a short section with the simplified (I'd say "obfuscating the physical contents") version. I will start this soon if you don't disagree. Then I will also correct the energy density expression, which stands there for quite a while now but does not correspond to S=ExH, only in vacuum... We must be blind...

AQv, "believe" seems to be the right word ;-) I can only guess what still makes you feel uncomfortable, but let me give one last thought: What about S=ExH if the "medium" consists of just a few atoms, and the concept of constitutive relations doesn't make any sense, and you cannot even do the averaging necessary to introduce the field H? Furthermore, do you think that E and B can be discontinuous at such a microscopic scale? Can they be discontinous in presence of 100, 1000, or a million atoms? - Let's now stop this thread here, it's neither the right medium nor the right place. -- Nebeleben (talk) 17:50, 6 August 2008 (UTC)

I'll allow myself one last(?) comment too then: In your paper you say that the force appearing in the time derivative of U_m is equal to the Lorentz force F = e(E + vxB). But, I wonder, if the same average E vector should be used for the bound charges as for the free charges? The large scale E will distort the cloud of bound charges around each atom (or molecule), and the bound charges will be affected both by the large scale E and the field from the nucleus and the other bound electrons in the same atom. What if these fields cancel in the sense that the average (over time) E vector the bound charges experience is zero? Then only the free charges contribute to the time derivative of your U_m, and the j_boundE part of j_totalE is perhaps more likely to be related to dipoles' potential energy.

Don't you find it strange that your U_e looks exactly the same for a given E and B, whether they are found in free space or in a material medium? In the medium (but not in free space) there is likely to be potential energy due to the dipoles' (both electric and magnetic) orientation in E and B. Still, you say that all potential energy is attributed to the fields, and that your mechanical energy terms only involve kinetic energy.AQv (talk) 13:02, 11 August 2008 (UTC)

It seems I constantly fail to anticipate your concerns and your understanding of the problem. That's why I offer (now for the last time, seriously ;-) ) to continue this discussion by mail. -- 1) There is no average or large scale field E. E is the microscopic field, and it is microscopically structured. What you are talking about applies rather to D and H. I admit this can be mind-boggling. 2) No, since it accounts for field energy only, I find it rather convincing, to be honest. 3) We're talking about electric potential energy which is always related to and "stored" in the fields. -- Nebeleben (talk) 15:02, 13 August 2008 (UTC)

You may turn out to be right, of course, but I fail to see how your paper actually proves that. A new S_e and U_e are suggested, and may be well motivated, but is there any form of corroboration from other parts of physics? Compare with the second quote from Furry in section 2 of this page.

"The idea that the Poynting vector is not to be taken seriously as a detailed distribution of energy flow and momentum density is a relic from the time when the energy-balance theorem for the electromagnetic field was taken as an isolated result. The single theorem indeed remains valid if one changes the Poynting vector by adding to it any vector whose divergence is zero. Such a change is clearly forbidden, however, by the theorems for momentum and angular momentum ..."

(I'm not sure if this has been done for anything but free space, so the question may still be open regarding non-free space.) My question is whether your S_e and U_e, as they are derived and presented in the paper, are to be interpreted, and presented in an encyclopedic article, as "suggested" or as "corroborated". Nothing wrong in presenting a new approach, but how verified is it?AQv (talk) 13:59, 14 August 2008 (UTC)

Forget every doubt I've expressed, I think I get it now. For some reason I didn't quite realize the scale of the resolution, that it's about subatomic, perhaps even infinite resolution, and that the new S_e and U_e aren't really new, but that on this scale the interior of matter looks very much like free space with some charged particles scattered around, and that it makes sense then to use the vacuum Poynting vector and energy density at this very local level. The speed of the local energy flux at this resolution will, I assume, be the speed of light in vacuum, even though we are inside matter, but, there being no such thing as homogenous fields at this subatomic level, the energy can't move straight, but will have to curve it's way through the interior, resulting in an effective large scale average velocity that will be lower than in vacuum. At this resolution there may be no discontinuities in the fields, except possibly at the "surface" of the charged particles, if these are thought of as point-like or small charged spheres, for example. If they have more diffuse boundaries, there might be no discontinuities there either. This very local energy flux is then coupled to the motion of the individual charged particles, rather than to any averaged current densities.

If the local energy density (ε₀/2)E² + (1/2μ₀)B² is to be integrated over a volume involving matter, then the actual fields at each point must be squared before (ε₀/2)E² + (1/2μ₀)B² is summed, so that for example the very strong fields near the nucleus are given their due weight. If the fields are averaged before taking the square, then (ε₀/2)E² + (1/2μ₀)B² would give the wrong result.AQv (talk) 11:44, 16 August 2008 (UTC)

It seems to me that the article is somewhat biased against the use of H in the Poynting vector, as opposed to B. It is true that the form involving B is valid on the microscopic scale, whether media is present or not. However in practical engineering problems, we usually work with macroscopic fields, and furthermore, we often do make the assumption that we have linear nondispersive media, including magnetic media. In this case the form of the Poynting vector with H is the one that should be used, and the one with B will give the wrong result. It is not true that, as stated in the article, the form involving H is practically limited only to vacuum. Elee1l5 (talk) 16:42, 8 October 2008 (UTC)

Appart from whether we use B or H, there is a question as to the validity of the WikiArticle in the case were the EM waves are not transverse, as it happens when there is total reflection in a non-conductor or when light goes from a non-conductor into a conductor. In both cases the wave vector is complex and so Maxwell's equation do not imply the usual orthogonality conditions among the real parts of E and H. I just add this as a warning, as in this case I haven't found a proof that one can still use the amplitud E and its complex conjugate to get the magnitude of S. —Preceding unsigned comment added by 62.83.111.63 (talk) 09:37, 12 September 2010 (UTC)

Alternate Expressions for Poynting Vector

There was no mention of the possibility of alternate expressions for poynting vector, e.g. a term which is a curl of some vector can be added to E x H keeping the Poynting Theorem valid. I think this bit is mentioned in Jordan Balmain. Also I have a paper by one Mr. Slepian in which he discusses several cases. Welt^anschaunng 19:09, 7 February 2008 (UTC)

Well, if you read a bit further up you'll see a long discussion about that topic. Apparently this invariance is not correct anymore in general relativity. There was some strong opposition against mentioning that invariance and I didn't pursue it anymore. Han-Kwang (t) 19:29, 7 February 2008 (UTC)

Radiation in a DC circuit

Recently this has been added to the article:

However, it is also known that power cannot be radiated without accelerated charges, i.e. time varying currents. Since we are considering DC (time invariant) currents here, radiation is not possible.

But the radiation can originate from atoms and molecules even if there are no large scale AC currents. In a DC circuit powered by an ordinary battery the energy primarily originates from the chemical electrode reactions. In a way one could think of the changes in electron states involved in these reactions as a kind of (sub)microscopic charge accelerations, not necessarily involving any macroscopic AC currents. Besides, any DC current will always create heat that radiates from a wire as electromagnetic heat radiation. To say that energy can't radiate within, or from, a DC circuit is simply wrong. In fact, materia kept at a temperature above absolute zero, it could be an ice cube at 5 K, will give of some thermal radiation in the form of electromagnetic waves, without there being any large scale AC currents involved. —Preceding unsigned comment added by AQv (talk • contribs) 17:53, 12 March 2008 (UTC)

What I learned in physics class is that there is an inducedd magnetic field inside a wire. This field would cause the particles to follow a spiral the wire. Because the magnetic force is always perpendicular to the path of the particles, it does not cause them to gain or lose energy. It does, however, accelerate them (centripetally). Also, the second paper cited for the section (the one numbered 7) refutes the one that supports the argument that the Poynting vector is not the right formulation (the one numbered 6). --Savant13 (talk) 21:28, 8 May 2009 (UTC)

The movement of charge in a dc circuit follows a closed path; it must, therefore, change direction. Change of direction is acceleration. Constant314 (talk) 12:13, 29 June 2010 (UTC)

Visual?

Does anybody have a visual?--Frozenport (talk) 17:56, 30 June 2008 (UTC)

What do you mean? Han-Kwang (t) 19:18, 30 June 2008 (UTC)

Rearrangement

I would like to propose a rearrangement of the article:

• Introduction
• Generalization
• Examples and applications
  • Coaxial wire
  • Value of the Poynting vector in plane waves
  • Poynting vector and radiation pressure
• Problems in certain cases
• References
• Further reading
• See also

Hopefully this is self-explanatory. If not, it's not a good proposal ;-) Comments? Nebeleben (talk) 09:32, 8 July 2008 (UTC)

For reference, this is the current article outline:

1 Interpretation 
1.1 Alternative form
2 The Poynting vector in electromagnetic waves 
2.1 Derivation
3 Radiation pressure
4 Examples
5 Problems in certain cases 
5.1 DC Power flow in a concentric cable
5.2 Independent E and B fields
6 Generalization
7 References
8 Further reading
9 See also

As I mentioned earlier, this article needs some clean-up and rearrangement, so in principle I'd welcome your initiative. I'm not sure how much rewriting you want to do, though. Since you are new here and maybe not aware of all Wikipedia conventions, or if you feel unsure, you could consider working on the re-vamped article in your user space, e.g. User:Nebeleben/Poynting vector and ask for feedback. I'll start with some feed-back here: (positive) you seem to know a lot about the subject and your edits so far were quite good. (negative) I'm not a big fan of the {{cite}} templates. They take a lot of space and make it harder to read the page source. I think there is a guideline somewhere that advises against converting existing references into the template version. Han-Kwang (t) 14:47, 8 July 2008 (UTC)

Thanks for your comments, Hankwang. Well, what I intend is a pure rearrangement plus a few better headings. I think the article will gain a lot this way without rewriting a single line. (I forgot to include sections 5.1 and 5.2 in the above proposal.) Regarding the citations, I read some guidelines, but besides the obvious "stick with one citation style" it seems a matter of taste to me. Nebeleben (talk) 18:36, 8 July 2008 (UTC)

OK, I'm not sure what content exactly goes where, but I'd say go ahead. If someone really disagrees, they might revert it and ask for discussion, but I don't expect so.

Regarding citation: from Wikipedia:Citing_sources#Citation_templates: The use of citation templates is neither encouraged nor discouraged. [...] Because templates can be contentious, editors should not change an article with a distinctive citation format to another without gaining consensus.; similar remarks in Wikipedia:Citation templates.

Han-Kwang (t) 19:21, 8 July 2008 (UTC)

I wish to say that as a new Wikipedian, I'm grateful for hints on policies and practises I might miss or offend. I agree with you that references in the running source are hard to read and maintain. However, I think that once references are made, the citation templates should be used so that the output format is uniform and the bibliographic data complete and possibly machine-readable. (Try, for example, the Zotero plugin [1] on a reference using/not using citation templates.) Nebeleben (talk) 21:04, 8 July 2008 (UTC)

Well, then we don't agree about the citations. I'd say follow the guidelines and use whatever citation style you prefer for new references, but don't update existing references except if they are really lacking essential information, like with url-only references. It would be better if the references are separate from the article text (like with LaTeX/bibTeX). If the MediaWiki software one day starts supporting that, I will immediately start using it. Anyway, for future editing, remember to be bold with articles that are clearly need more work. Han-Kwang (t) 10:33, 10 July 2008 (UTC)

Neutral Point of View, NPOV

The reason I've been asking all the questions about Nebeleben's paper is not because of a strong personal interest in the paper - in that case this would not be the right place, as have been suggested. The paper is a refereed published paper, and in that sense a valid reference, but I'm worried that he might be a bit biased when it comes to presenting the content of his paper. The paper being refereed doesn't make every suggestion made in it into a widely accepted truth, and it is questionable to suddenly have a new definition of the Poynting vector that doesn't coincide with the old definition for material media whose electric and magnetic properties can be characterized by scalar μ and ε. The derivation in the paper suggests an identification of a certain term as the real, new em Poynting vector, but I wonder if this should be presented on the article here as being the actual/true em Poynting vector. Is one refereed paper enough to change the classical definition, and make all the claims that are being made, or is more support needed first? A research paper is probably allowed to be more biased than an encyclopedic article. I'm wondering if Nebeleben is keeping a sufficiently "Neutral Point of View", or if there is a tendency to promote his own research. (See for example Wikipedia:Neutral_point_of_view and Wikipedia:NPOV_tutorial.) It's difficult for me to judge, but I suspect there might be a tendency of selfpromotion in his contributions.AQv (talk) 15:54, 12 August 2008 (UTC)

Vague Wording

In the section referring to the nature of the two terms in parentheses, ${\underline {E}}\cdot {\underline {D}}+{\underline {B}}\cdot {\underline {H}}$, the second term is given the less-than-artful interpretation as the "negative of work done by ...". I think the term "subtrahend," or perhaps "subtracted portion" could be put to good use here. I'll be changing that right now; here is where to object. Eccomi (talk) 02:20, 27 October 2008 (UTC)

Auxiliary field strength ?

In the very first paragraph, the vector H is called auxiliary field strength. I think, the adjective auxiliary is quite meaningless. This is a phyisical quantity and like all other phyisical quantities it is a convenient tool to solve the problems. There is no reason to name it auxiliary. Nedim Ardoğa (talk) 11:43, 4 February 2010 (UTC)

Poynting Vector Tilted

In the section "The Poynting vector in a coaxial cable" I think "tilted" is not the best word, because it is usually applied to rigid structures and might suggest to some readers that the Poynting vector everywhere points at the same angle toward the center conductor. Also, a resistive center conductor and a zero resistance outer conductor is a special case. If both were resistive and we wanted to use "tilted" then we have the Poynting vector tilted in two directions at the same time. I would like to generalize the statement by changing "core conductor" to "a conductor" and elaborate the tilting occurs near the surface of the conductor. I suggest the following: "If a conductor was replaced by a conductor having significant resistance, then the Poynting vector would become tilted toward that conductor near the surface of that conductor." Constant314 (talk) 14:48, 8 August 2010 (UTC)

Archive 1

Archive 2

Archive 3