Talk:Positive feedback/Archive 1

Archive 1

Archive 2

The author of this article

hello, i was just wondering who the author of this article is? i need to know for referencing the information for my essay. thank-you very much. my e-mail is teenateichroeb@yahoo.com

Greetings. There is rarely any one author per se on any given Wikipedia article. I direct you to this page which talks about the best way to go about citing Wikipedia. Have fun! RadicalBender 16:35, 8 Mar 2004 (UTC)

Untitled

Rated "high" as high school/SAT biology content. This article needs biological/biochemical examples of feedback regulation, e.g. of enzyme activity or gene expression. It also needs references. - tameeria 00:19, 19 February 2007 (UTC)

games?

I don't understand the gaming examples. --Abdull 21:33, 21 July 2005 (UTC)

I'm not sure how to improve the explanation. The idea is that there's an "upward spiral", where improvement in the player's position leads to more and more rapid improvement. Please feel free to edit it, or maybe visit your bookstore and take a look at the source, Rules of Play. Deco 03:55, 23 July 2005 (UTC)

These might be good examples in gaming but they're not very good examples. Why do we need examples specifically from gaming anyway? I think the rest of the article does fine. Deleting. Every name is taken12345 09:22, 4 April 2007 (UTC)

surely this gaming example is trivial. It adds nothing, so I'm removing it. —Preceding unsigned comment added by 85.134.134.152 (talk • contribs)

In biology

One example of a biological positive feedback loop is the onset of contractions in childbirth. When a contraction occurs, the hormone oxytocin is released into the body, which stimulates further contractions. This results in contractions increasing in amplitude and frequency.

Another example of a biological positive feedback loop is the process of blood clotting. The loop is initiated when injured tissue releases signal chemicals which activate platelets in the blood. An activated platelet releases chemicals which activate more platelets, causing a rapid cascade and the formation of a blood clot.

In most cases, once the purpose of the feedback loop is completed, counter-signals are released which suppress or break the loop.

safe safe — Preceding unsigned comment added by Mdd (talk • contribs) 15:09, 16 May 2008‎ (UTC)

Is it unstable if gain is less than one?

Article says "A system in equilibrium in which there is positive feedback to any change in its current state is said to be in an unstable equilibrium, whereas it is possible for one with negative feedback to be in a stable equilibrium."

What if the gain is less than one. In climate terms a positive feedback with gain of less than one is considered a stable climate. Is this different in other disciplines? crandles (talk) 16:04, 17 February 2009 (UTC)

ANSWER: In the context of the quoted text, "negative feedback" and "gain of less than one" are synonomous. "Negative" doesn't necessarily mean that the absolute value of the feedback is negative, but rather the mathematical derivative of the feedback value is negative with respect to time. -MWies —Preceding unsigned comment added by 205.174.162.35 (talk) 17:43, 16 September 2009 (UTC)

That makes no sense. Positive feedback should simply be feedback which self-reinforces. In simple cases, if the feedback factor is smaller than 1 this means amplification, and the output is greater than the input but does not grow infinitely; if the feedback is greater than 1 then it does grow without limit. Negative feedback is similar, it is feedback which attenuates and if it is between 0 and -1 then it simply means the output is smaller than the input, with unstable oscillations if more negative than -1. One problem is that phrases like gain and loop gain are used in more than one sense. --Rumping (talk) 22:34, 3 February 2010 (UTC)

Spiralling

The second line of the lede says "it will tend to spiral out of control". This is an inappropriate metaphor for such a prominent position in the article. I would suggest something like, 'Under strong positive feedback, most systems quickly move to a limit state, where the limit is provided by external factors, or into some other new stable state where the positive feedback is somehow negated.' Does anybody here have a better or more general wording that does not involve spiralling or any other unlikely convolutions? --Nigelj (talk) 13:23, 5 March 2010 (UTC)

Well a week has gone by and nobody has objected or suggested anything better, so I have made the change. While I was at it I tidied up some other wording in the lede. --Nigelj (talk) 13:35, 13 March 2010 (UTC)

Ferguson Reflex

Altered 'in biology' section slightly in order to link to the Ferguson reflex, which is the name of the contractions mentioned. Medical Sciences (Edited by Naish, Revest and Court) is where I found this, in the endocrinology chapter. —Preceding unsigned comment added by 138.253.88.75 (talk) 22:28, 3 November 2010 (UTC)

A flip-flop/latch is NOT positive feedback!

Positive feedback in dynamic systems has a additive or multiplicative effect. A latch built with NAND or NOR gates fails the test for positive feedback in 2 ways. 1: The bubble on the end of the gate is an inverter. Thus, the feedback is negative, not positive. 2: digital (logic) feedback is not accumulative/multiplicative as it is with e.g., thermal runaway. --Bill Huston ^(talk)

Illustration of an R-S ('reset-set') flip-flop made from two digital nor gates with positive feedback. Red and black mean logical '1' and '0', respectively.

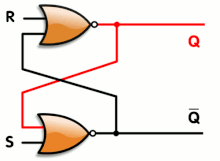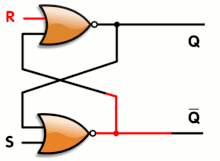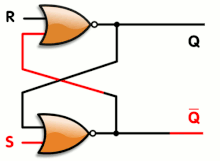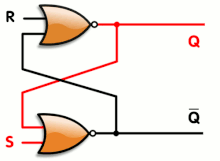
That is wrong. I have included that diagram here to help this discussion. First, notice two little bubbles. From the input next to the S, you go through the bottom inverting gate, then the top one before coming back to the input next to the S, that's two inversions of sense and so is positive feedback. Second, who heard of a circuit being held in a limit-state, with all outputs hard against the supply rails, with no input and negative feedback? The only thing that drives every component in a circuit against the rails and keeps it there is positive feedback (or an extreme input, which is not necessary for a latched flip-flop). Third, we think of logic gates as 'digital' with only two states, but they don't know that; they are made entirely of analogue components inside the chips - MOSFETs or other transistors, diodes or resistors. You can make a flip-flop out of any low-gain analogue transistors and it will latch hard against the supply rails as soon as you switch it on, that's only because of the extreme positive feedback having additive and multiplicative effects. Here are two references that support this explicitly: [1] and [2] , from a simple google search. I'm going to reinstate the section, per WP:BRD. See if you can find a reference that says flip-flops latch because of negative feedback. --Nigelj (talk) 20:46, 4 November 2010 (UTC)

In biology

I moved the material on psychology to a new 'In psychology' section. So revealed, it is sorely lacking, having discussion of two references on gifted children, and nothing else. What was left in the biology section, I split into physiology and evolutionary biology subsections. I deleted some editorial asides and original research/synthesis. Robertmacl (talk) 19:07, 29 December 2010 (UTC)

Preamble should being: "Positive feedback is ....."

Preamble should being: "Positive feedback is ....", an active voice declaration, an assertion. Right now we have instead an example:

A system exhibiting positive feedback, in response to perturbation, acts to increase the magnitude of the perturbation.

In addition, the word "perturbation" while precise, does not lend to clarity for the average Wikipedia user.

I am going to take the suggestion to "BE BOLD" and going to take a whack at improving this. — Preceding unsigned comment added by Bhuston (talk • contribs) 19:29, 20 August 2011

Re the changes to the lead, while I agree with the editor that the correct format would begin with a definition, the one provided is not understandable to me, and likely not understandable to the majority of non-specialist readers. I have no idea what phase-congruent means, despite having an intuitive idea of what positive feedback is about. Per WP:MOSINTRO, can we come up with an introductory text that does not use overly specialized terminology? Quasihuman | Talk 21:38, 26 November 2011 (UTC)

The above two comments are a little hard to follow. I think Quasihuman is saying that the current lead is not helpful, and that the old lead was better (that is, the change in this edit by Bhuston is not desirable). The old lead started:

A system exhibiting positive feedback, in response to perturbation, acts to increase the magnitude of the perturbation.

while the current lead starts:

Positive feedback is energy taken from the output of a system and reapplied to the input, which is phase-congruent with the input signal.

I agree that the opening sentence of the old lead is better. I have not yet thought about the rest of the lead, but it is too long (and may not be just a summary of points in the article, per WP:LEAD). Johnuniq (talk) 02:31, 27 November 2011 (UTC)

In these edits, I have found a way to use the current opening sentence, but have the sentence begin 'Positive feedback is...'. I've also added a few links - one to Wiktionary. I've tried to make the distinction between erroneously saying 'positive feedback is...' when 'the effect of positive feedback on a system is...' is more accurate. I've tried to do this without being unnecessarily wordy or pedantic. I can discuss individual changes if anyone wants me to. --Nigelj (talk) 22:58, 27 November 2011 (UTC)

Where the preamble says ..."positive" refers to the mathematical sign of the direction of change..., is this being too specific? In general, it seems the magnitude of the change is important, not the direction. Otherwise, this excludes things like market crashes or latches switching off. --Trevithj (talk) 22:34, 14 March 2012 (UTC)

Cause of oscillation?

Positive feedback tends to cause ... oscillation. Really? This seems self-contradictory. Why would something that causes a system's output to move away from an equilibrium suddenly cause it to about face and head back there (multiple times)?

Some authors (John Sterman and Peter Senge) even state that oscillations are explicitly caused by Negative feedback instead. The section on Hunting oscillation outlines this.

This may relate to a point made earlier by User:Rumping: "One problem is that phrases like gain and loop gain are used in more than one sense." A similar issue is being raised at the Electronic oscillator page. If no objection I would like to (1) remove the oscillation reference and (2) add some clarity on the use of "positive" and "gain" as applied in this context. Trevithj (talk) 21:58, 8 March 2012 (UTC)

That statement, I think, comes from the lede, where it is describing the concept at its most general. One justification for the inclusion of oscillation in the list might lie in complex systems, where the overall situation is the net result of an interplay between a lot of positive and negative feedbacks. In such a case case, increasing the effectiveness of a positive feedback would have an effect similar to that of increasing the loop gain in a simpler negative feedback system, i.e. it could push a barely stable system just into oscillation. --Nigelj (talk) 22:47, 8 March 2012 (UTC)

Another possibility is to do with the non-linearities that may exist in a real system near the edges of its capability: positive feedback that drives a system powerfully away from the central region may peter out and die to nothing near the edges, allowing 'inertia' to drive an overshoot before the system begins to fall back to the centre (perhaps there's negative feedback involved in that bit?), at which time the positive feedback builds in strength again. I once fixed a fault in a shaft position control system where the sense of an amplifier had been wired reversed - causing very strong positive feedback instead of the expected negative FB. The shaft sensor produced -5 V for 0°, 0 V for 180°, and very nearly +5 V for 359.9°. The non-linearity between 359.9° and 0° made the system oscillate violently about that point with positive feedback whatever the setpoint! --Nigelj (talk) 22:58, 8 March 2012 (UTC)

Hi Nigelj. Yes, that statement comes from the current overview - is that what you mean?

Your examples highlight another difficult area: positive feedback may exaggerate an already existing oscillation, but can we say it causes the oscillation? Also, if frequency and amplitude are fairly constant, in what sense is an oscillation unstable?

Your shaft position-control is a good case in point. Can we say the shaft oscillates when the system is stable? I'm questioning frames of reference here. Trevithj (talk) 00:07, 9 March 2012 (UTC)

If you have two dimensions, x and y, or displacement and momentum, you can find that positive feedback can cause the value to spiral away from equilibrium. That will appear as an ever-increasing oscillation amplitude.GliderMaven (talk) 23:49, 8 March 2012 (UTC)

So it never completely goes back to zero. If the displacement is zero, then the momentum isn't, and in fact each time it returns to zero displacement, the momentum is bigger each time.GliderMaven (talk) 00:02, 9 March 2012 (UTC)

Hi, GliderMaven. Similar response to above - isn't the oscillation already there? You raise another interesting point though: in what sense is the feedback "positive" with x and y dimensions? Trevithj (talk) 00:07, 9 March 2012 (UTC)

No, there need not be anything you would recognize as an oscillation. The feedback is positive in the totally normal sense. And very many common situations are two or more dimensional, where the amplitude grows over time.GliderMaven (talk) 01:19, 9 March 2012 (UTC)

@GliderMaven, sorry but I don't understand your first response. Why does the feedback spiral away?

I think I get your second point - assuming the "totally normal sense" of positive = "increasing". Do you mean that positive feedback causes a state in x,y space to move further away from the origin (vs. moving in a "positive direction" along either axis)? Trevithj (talk) 01:41, 9 March 2012 (UTC)

Yes, in the totally normal case that is very, very commonly found, the positive feedback doesn't act directly away from equilibrium, it acts at an angle in the x/y diagram or on the position/velocity diagram to the origin, and on that diagram you end up with a spiral, which will appear as an ever growing oscillation. And that's very definitely positive feedback. For example, on aircraft wings, they sometimes get aeroelastic flutter which is a form of positive feedback on an aerodynamic surface which often continues until the wing falls off. That would appear as a spiral on a speed/position graph as it grows.GliderMaven (talk) 03:22, 10 March 2012 (UTC)

Hmm. I accept that this is common, and that the net outward movement is due to PF. It is still difficult to see why PF would cause spiraling if the system wasn't already doing it. Also, a system with NF (or no feedback) could also spiral (inward). Not reinforcing, sure, but still oscillating. Trevithj (talk) 08:07, 10 March 2012 (UTC)

I don't know where this discussion is heading - it should be focussed on improving the article per WP:TPG. In answer to the questions aimed at me above, the reason I mentioned the position of the statement is that that is where the article is at its most general - i.e. it is not just about electronic oscillators or any other specialist area. Both my examples were about +ve FB causing an oscillation. Just because a system has a natural resonant frequency, or the capacity to oscillate, doesn't mean that 'the oscillation [is] already there' in any real sense. I used the word stable as a control system engineer - a system that oscillates (for ever or for too long) when it's measured value meant to be steady, is too unstable in that sense. Oscillations don't have to continue to grow with time for the system to be oscillating. I think it's more useful to stick to the problem you see in the wording of the article (per WP:TPG - talk page guidelines), which was can positive FB cause oscillation, rather than stray into intricacies of instability, or multidimensionality, or frames of reference. --Nigelj (talk) 00:02, 10 March 2012 (UTC)

If my questions have come across as belligerent, I apologise. That wasn't my intention. I admit I am somewhat frustrated by this subject, but I do want to try and pin down points of confusion. The examples you have given above are very thought-provoking and interesting. When I said your shaft-control example was a "good case in point", I meant it was (and is) a good scenario to examine.

The original difficulty remains. If PF (by definition) reinforces effects, how can it reinforce an effect which isn't there? I see it as definitely an issue of general definition.

My research on this found references to oscillation being caused by NF, yet the opposite idea persists across several articles. So I'm trying to get at the underlying thinking, which I assume involves a conflict in frames of reference (which often happens). If so, I hope to make this explicit, which should improve the article. If my research is wrong, I want to know about that too. Trevithj (talk) 08:07, 10 March 2012 (UTC)

If there's only one dimension of the phase space, then no amount of feedback can EVER cause oscillation. If there's two or more then it can certainly cause oscillation. Takoma Narrows is a classic example.GliderMaven (talk) 03:22, 10 March 2012 (UTC)

OK, I'll go along with this for a while. Re, positive feedback "reinforces effects, [so] how can it reinforce an effect which isn't there?" You may be thinking about a static system that is actually very unstable. Think of a matchbox balanced on its end rather than its side - it is less stable and so requires less perturbation to tip it into a new state. Now think of it balanced on its corner! Utterly unstable, but in theory possible to do. The slightest perturbation and it'll go. In what I think GliderMaven is calling a 2-dimensional system (we called them either 2nd or 3rd order systems - ones that have d2x/dt2, d3x/dt3 or higher terms in their equations and so are capable of oscillating) the 'new state' after such a perturbation is often one of oscillation. Maybe imagine an inverted heavy pendulum, held upright by two weak springs. The springs provide negative feedback to hold it in place, but its mass provides positive feedback pulling it away from centre. It can be stationary, it can oscillate gently, and a heavier perturbation can send it all the way to one of its endstops - either directly or after a few increasing oscillations.

Aeroelastic flutter is an interesting case. I'm a sailor and there is a rule when sailing downwind, never to let the top of any sail sag off the wind at more than 90 deg to the centreline of the boat, or you make a 'rolling machine'. It goes like this: when the boat rolls one way, the sail remains stalled and produces drag, a down-wind force, but when it rolls the other way the flow can become laminar again and produce lift, which has a component at 90 deg to the wind. With sails let out too far, this lift will exaggerate the roll of the boat that caused it. --Nigelj (talk) 14:40, 10 March 2012 (UTC)

Thank you - again you provide useful examples. The sailing example (and maybe aeroelastic flutter) sound similar to Dutch Roll: like two effects chasing each other. Maybe not - I'm no sailor - but I once traced a pair of recurring software bugs that were doing that; the cure for one caused the other.

I get that a big enough perturbation can knock a system into a different state. Thinking about the inverted pendulum example (without the springs/stops) I guess we could say that a perturbation would flip the pendulum into its more usual configuration - which certainly oscillates. Hmm.

Okay, if PF moves a system away from a non-oscillating state into an oscillating state, and in the process provides the kick to get the oscillation going, then its reasonable to say that PF is a contributory cause of the oscillation. Is it a necessary or sufficient cause? (If not, does that matter here?) -- Trevithj (talk) 03:31, 11 March 2012 (UTC)

I have moderated my original position, and concede that PF is an important contributory cause to oscillation. Have edited the lead section from "oscillation" to "extreme oscillation", and will leave it at that. Thanks for the feedback critique. Trevithj (talk) 22:19, 13 March 2012 (UTC)

No, in most cases if the state of the system is anywhere on that graph except at exactly the equilibrium, then net positive feedback will cause ever growing oscillation, and in that sense the feedback directly causes the oscillation. It doesn't cause it to be away from the equilibrium position, but it 100% definitely can cause the actual oscillation.Teapeat (talk) 22:47, 14 March 2012 (UTC)

If cause means either trigger or enhance, then PF can cause oscillation. But if cause means necessary or sufficient, then PF is neither. If oscillation doesn't necessarily imply PF, and PF doesn't guarantee oscillation, we can't call it 100% definite. -- Trevithj (talk) 01:20, 16 March 2012 (UTC)

Use of 'ideal feedback model'

I would like to propose that this diagram (in its current form anyway) be moved out of the lead. Despite its implied generality, I believe it is actually quite specific to electronics. It uses a definition of feedback type that is not generic - the sign of the feedback signal (Nyquist and Bode), and is very likely based on Black's and Bode's work related to the negative feedback amplifier. While very important in the development of the concepts of positive/negative feedback, this work introduces some confusion here: this article is specific to positive feedback, while the model is associated with negative feedback.

It also doesn't work easily with examples given. It is not obvious what the inputs/outputs are of a cattle stampede, nor how the β function would apply to the feedback. A simpler two-attribute causal loop diagram would work - e.g., number_of_animals_running and overall_level_of_fear reinforcing each other.

I agree that a clear diagram is a good idea in the lead. The other lead images depict specific examples of positive feedback, not generic models, so I had added the simplest diagram I could find, using the example of compound interest. The diagram was easy to follow, uses a familiar example, and is of a form commonly used in system dynamics literature to explain the concept.

As my initial edit was reversed, I ask for wider opinions on this suggestion. -- Trevithj (talk) 21:58, 18 April 2012 (UTC)

Added an example diagram as described above, to illustrate the existing stampede example. -- Trevithj (talk) 23:31, 2 May 2012 (UTC)

Moved image as discussed. Added cited text, based on only published reference that I could find for "ideal feedback model" other than wikimedia (W Chen 1993), although likely based on Hendrik Bode's work. -- Trevithj (talk) 21:31, 7 May 2012 (UTC)

Positive feedback always acts away from an equilibrium

By definition, positive feedback itself creates a disturbance that is a positive function of the distance in phase space from an (unstable) equilibrium.

So if there's a small disturbance that is away from equilibrium, it is amplified; but if there's a small disturbance towards equilibrium, it is going to be opposed, cancelled or in cases of large positive feedback, overwhelmed.

So positive feedback does not alway increase the size of a disturbance, only the disturbance measured from equilibrium.

Is this even remotely controversial??? GliderMaven (talk) 14:27, 27 May 2012 (UTC)

You know it is, because I reverted you. I'm not familiar with this definition. Can you provide a source? What about distrurbances that push a system back toward equilibrium? Doesn't positive feedback accelerate that (and cause overshoot in many cases)? If the system is linear, the direction of the disturbance doesn't matter; either way, it gets increased by positive feedback. And what about systems that have no definable equilibrium state? Dicklyon (talk) 16:52, 27 May 2012 (UTC)

(e/c) I think in order to understand this, we need to imagine a system that:

1. includes one or more positive feedback mechanisms
2. is not at equilibrium (no matter how unstable)
3. is then subject to a small perturbation, either (a) away from equilibrium or (b) towards it

I'm finding it very difficult to imagine any real world example that satisfies (1) and (2), let alone bring (3) into it. This may have some abstract mathematical reality to it, but I'm unimpressed without something more concrete. Our present definition is really based on (1) and (3a), without the requirement that the system is already in motion (2) which would be required in order to give a disturbance towards equilibrium (3b) any meaningful reality. --Nigelj (talk) 17:44, 27 May 2012 (UTC)

How about the example of compound interest on an investment? Equilibrium would be zero principal (so ... no investment!) Changes in principal would be the perturbations. Any value of $ > 0 would serve as a reference point for future growth ('accelerating' the balance away from the starting value).

GliderMaven has a point regards using equilibrium as a reference point - provided that is feasible. Other options exist however. Also, defining ANY change with respect to equilibrium may in fact be a tautology: "a net change causes divergence from a point of no net change." -- Trevithj (talk) 01:39, 1 June 2012 (UTC)

OK, so imagine an inverted pendulum, with a loose thin thread tying it to an upright vertical support. First the pendulum is released from upright. The further it falls, the greater the moment accelerating it (+ve FB). Then the thread pulls tight and it is perturbed towards the upright, unstable equilibrium point. The thread breaks, the downward swing continues, but it has been slightly slowed and delayed by the thread. Yup. A perturbation that was not exaggerated by the +ve FB. A little bit like introducing, say, carbon trading into a world headed for unstoppable global warming due to carbon emissions, maybe. --Nigelj (talk) 17:52, 27 May 2012 (UTC)

Re Dicklyon's questions: To define feedback as either positive or negative requires a comparison between a measured value and a reference value. If the difference between them is increasing, the feedback is positive. By that definition, there is no explicit requirement for amplification to be involved. And equilibrium may be too jargon-ish - why not say reference?

Note that this applies specifically to the cybernetics paradigm. None of the above applies to the performance appraisal/psychology paradigm, which also uses the term "positive feedback" very frequently, but applies it to the mechanism rather than to the result (and that is another old controversy). --Trevithj (talk) 19:59, 27 May 2012 (UTC)

I agree that there is no need to invoke 'amplification' or 'equilibrium', but disagree about this proposed definition. Take an oven - measured temperature 180°C, setpoint or reference value 200°C. If this difference is increasing, there is no need for there to be positive feedback. The heater could have failed, the door may be open, or the setpoint could be ramping quickly upwards. Positive feedback requires that some part of the system is detecting this difference and applying a cooling influence because of the negative difference. If negative differences => cooling, and positive differences => heating, that would be positive feedback in this case. --Nigelj (talk) 21:14, 27 May 2012 (UTC)

Good point. To clarify, the definition assumes feedback. But for a clearer explaination, see (Ramaprasad 1983). --Trevithj (talk) 23:11, 27 May 2012 (UTC)

Unfortunately, a reference value is only one example of an equilibrium. In the general case in systems the unstable equilibria are a manifold in the phase n-space; in chaos theory, I think that's sometimes called a 'strange repeller'. The phase state in n-space undergoes positive feedback away from the strange repeller and ends up moving towards the strange attractor.GliderMaven (talk) 01:56, 28 May 2012 (UTC)

It might be clearer to say that an equilibrium is only one example of a reference value. Given that an n-space system would likely have a great many feedback loops, this doesn't really serve to clearly explain the concept covered by the article. It's a fascinating area (phase states in n-space), but probably belongs in its own article.-- Trevithj (talk) 02:40, 28 May 2012 (UTC)

I suppose a simple example in one dimension would be thermal temperature of a CPU. If the temperature is above a certain equilibrium value the silicon will conduct and warm up and the temperature will runaway until the chip cooks. If the temperature is below that point, the temperature will go down towards a stable equilibrium.GliderMaven (talk) 01:56, 28 May 2012 (UTC)

Thermal runaway is a good example. Note that you are using two reference values here, both called "equilibrium". Its not so much controversial as confusing. -- Trevithj (talk) 02:40, 28 May 2012 (UTC)

Here's a ref on a positive-feedback amplifier that has neither a reference point nor an equilibrium per se. For any given input level it does have an equilibrium output value, but the effect of the positive feedback on perturbations doesn't depend on which direction they are in. Dicklyon (talk) 05:16, 28 May 2012 (UTC)

I can't read the example online, so it is difficult to comment! Don't regenerative amplifiers implicitly use gain (ratio input:output) as a reference value? -- Trevithj (talk) 07:26, 28 May 2012 (UTC)

I can't read it either.GliderMaven (talk) 11:40, 31 May 2012 (UTC)

I guess it's not available in all countries. Dicklyon (talk) 03:46, 1 June 2012 (UTC)

"What about distrurbances that push a system back toward equilibrium? Doesn't positive feedback accelerate that (and cause overshoot in many cases)?"

No of course not!

Positive feedback opposes and attenuates forces that push a system back into equilibrium, that's the whole point!!!

Yes, you can get some systems to exhibit overshoot and oscillations in positive feedback systems with 2 or more dimensional phase spaces, (e.g. position and momentum), but a disturbance that pushes a system towards equilibrium in both dimensions has a damping effect!!!GliderMaven (talk) 11:40, 31 May 2012 (UTC)

Is there a source that describes positive feedback as you understand it? Dicklyon (talk) 03:46, 1 June 2012 (UTC)

While I disagree with the generality of "equilibrium" as a reference point, and feel that GliderMaven's comments are less than civil, he is correct in saying that positive feedback will always increase a discrepancy. Ramaprasad (cited above, pg9) says: "if the action triggered by feedback widens the gap between the reference and actual levels of the system parameter, the feedback is called positive feedback." And Carver says "A positive feedback loop ... is a discrepancy amplifying system. These loops create movement away from the reference value".

Charles S. Carver, Michael F. Scheier. On the Self-Regulation of Behavior. Cambridge University Press, 2001 pg18

As for overshoot/oscillation - that is a very confounding issue! See above section. Hope that is useful. --Trevithj (talk) 04:15, 1 June 2012 (UTC)

It's not very confounding from the point of view of linear/nonlinear systems theory, where the feedback can be positive and negative at different frequencies. The confounding thing is when the behavior guys try to adapt systems concepts to their fields. Your book ref seems to be largely about stable and unstable equilibria. The latter might arise by positive feedback, but systems with positive feedback are not necessarily unstable. It's a too-narrow viewpoint and definition. But even there, what I was saying is true. Consider the balanced-pencil example. If you disturb it away from equilibrium, the torque due to gravity increases and pulls it harder away from equilibrium. But if you knock it toward equilibrium, the torque due to gravity decreases, pulling it less hard away from equilibrium. In both cases it's positive feedback amplifying the disturbance, not dependent on the direction. Dicklyon (talk) 04:24, 1 June 2012 (UTC)

This is a very odd definition of 'amplifying'. Note that the loop gain in a positive feedback system can often be a lot less than one, so as to not be an amplification, but an attenuation.

No. What matters most is the direction of the feedback, not the amplification, the feedback direction is always designed to be away or towards equilibrium (or a reference if you prefer.) Positive feedback is NOT an amplifier!GliderMaven (talk) 10:06, 1 June 2012 (UTC)

But positive means in the same direction as the input (or disturbance). It doesn't matter which direction the input occurs in. Dicklyon (talk) 14:44, 1 June 2012 (UTC)

rather than adding tags to the whole article (most of which consists of specific examples which are not in dispute), why doesn't somebody (e.g. GliderMaven) propose a new definition for the opening lines, with a source, and we can knock it into shape here. This is meant per WP:TPG, re 'improving the article'. --Nigelj (talk) 19:04, 1 June 2012 (UTC)

The problem is that amplifying perturbations is not characteristic of positive feedback, it's only one characteristic, and not even the most important one. The important characteristic is that there's positive force that goes as a function from the distance from an equilibrium/reference.GliderMaven (talk) 12:44, 2 June 2012 (UTC)

Not a perturbation, which is by definition an infinitely small quantity, it's a disturbance, disturbances don't have to be small.GliderMaven (talk) 12:44, 2 June 2012 (UTC)

"Positive feedback in a system is a process in which a disturbance away from equilibrium has the effect of increasing the magnitude of the disturbance. That is, A produces more of B which in turn produces more of A"

GliderMaven (talk) 12:44, 2 June 2012 (UTC)

Who are you quoting? It sounds like it's describing an unstable equilibrium, which doesn't necessarily come about via feedback, but can result from a sufficient quantity of positive feedback. Lower amounts of positive feedback are sometimes used, leaving a system stable. Dicklyon (talk) 18:59, 2 June 2012 (UTC)

section break

For a long time (until this unexplained edit, and some editing that followed), the opening sentences read, "Positive feedback is a process in which the effects of a small disturbance on (a perturbation of) a system include an increase in the magnitude of the perturbation. That is, A produces more of B which in turn produces more of A." So the main changes I see GliderMaven proposing are as follows:

1. add 'in a system' so we say "Positive feedback in a system is a process...
2. remove 'effects... include', to say 'has the effect of'
3. add 'away from equilibrium'
4. remove 'small' from 'small disturbance'
5. remove both mentions of 'perturbation'

Re 1, I don't see any benefit. Re 2, the previous wording was careful to distinguish the effect of the feedback from the effect of the disturbance - we are defining only the former (without knowing more about the system, we can't really speak for the latter). Re 3, This is the change that has been under discussion on this section from the start. I'm not sure we can introduce 'equilibrium' undefined into this definition with begging more questions than we answer - it caused enough confusion among us just above. Re 4, I don't know, I guess that whatever the +ve FB does to a small disturbance it will also do to any size one, but large disturbances can have unexpected side effects, which I think is why control theory often talks about 'small' disturbances or perturbations (I don't think they have to be infinitesimal, just not so big as to have multiple or irrelevant side effects). Re 5, see my comment re 4. --Nigelj (talk) 23:41, 2 June 2012 (UTC)

I agree with your assessment. In the technical fields, we talk about small perturbations because then things tend to be locally linear, making it easier to reason about. What happens with large disturbances is arbitrarily more complicated, making it hard to say where feedback is effectively positive or negative, for example. I think that GliderMaven is coming from the social sciences, where they don't tend to get very analytical or numerical. Dicklyon (talk) 23:47, 2 June 2012 (UTC)

An example of positive feedback:

${\dot {x}}=f(x+\delta x)$

where $\delta x$ is a perturbation, and f() is an arbitrary function, which may be nonlinear, positive when x>0 and negative when x < 0

Now, the claim in the first sentence is that positive feedback is such that delta x is amplified. But it may be seen that a valid f() to give positive feedback is when it can be a constant positive value above zero, and a constant negative value below zero and the system still constitutes positive feedback, without amplifying any perturbations at all (except around the equilibrium point).

How many different ways do I have to say the same damn thing, that the first sentence is false?

The first sentence is Original Research, not backed up by any references, and it is NOT at all correct!!! Positive feedback occurs, always, with respect to an equilibrium or 'reference'. That's also what the reference says "A positive feedback loop ... is a discrepancy amplifying system. These loops create movement away from the reference value" GliderMaven (talk) 16:32, 3 June 2012 (UTC)

Yes, you can make hash of almost any dynamical systems concept by trying to apply it to non-differentiable functions. If you take a smoothed version of your function, you'll see a region near zero where it tends to amplify disturbances; and when it goes flat, there's no longer any positive feedback there. Dicklyon (talk) 17:40, 3 June 2012 (UTC)

I don't accept your faulty argument, and your definition and argument is OR, and doesn't match the reference.GliderMaven (talk) 18:10, 3 June 2012 (UTC)

Many of the examples here and in the article have no reference point (in the sense of 'required value' or 'setpoint') and no equilibrium point (except perhaps a trivial and largely irrelevant zero-point). The include:

• Compound interest - the equilibrium point is zero investment, at which point it's not really an investment account
• Stampeding animals - equilibrium is zero animals stampeding - no stampede
• Contractions in childbirth - equilibrium at no contractions - not during childbirth
• Thermal runaway - equilibrium when cold
• etc

There are obscure cases where this piece of pure maths has a relevance to reality (e.g. my inverted pendulum and thin thread example above), but the definition has to be general - i.e. apply to all cases, not just to one theoretical mathematical model and to one convoluted and contrived example. I would be happy to see a textbook definition, but I do not accept the one you are quoting, or the changes you are proposing. I think that author is talking about +ve FB in his specific application, not defining it in general. --Nigelj (talk) 18:28, 3 June 2012 (UTC)

He is stating properties of a feedback system that are held, by him, in a reliable published work, to be true. I'll take that every time over what you, or Dicklyon says, anytime. If you will not stick to reliable sources, please leave.GliderMaven (talk) 18:30, 3 June 2012 (UTC)

There is no need for your continuing level of incivility. That is the second time you have been warned in the course of this one discussion. I had some further thoughts about where your confusion may be arising, but considering your attitude, I think I'll keep them to myself for now. You have no consensus to make the changes you have proposed. If you have any further suggestions for improving the article, please start a new section here to discuss them. --Nigelj (talk) 18:42, 3 June 2012 (UTC)

Settle down there and WP:AGF. Sticking to sources is what we're all about. If you've said what your source is, I missed it; I asked above who you are quoting, and I've started a section below to collect relevant sources with good definitions. Dicklyon (talk) 18:42, 3 June 2012 (UTC)

And the example I give above isn't some theoretical model, it's a standard, common, real world cybernetic system called a 'bang-bang controller'. They're normally wired up in negative feedback mode, but if you simply swap the connections to the motor around, or similar, then it forms a positive feedback loop. The important characteristic of it is that it doesn't amplify perturbations, it just runs the motors at a constant speed.GliderMaven (talk) 18:40, 3 June 2012 (UTC)

Sure, it's an odd limiting case of positive feedback; but the feedback is only at the point of the discontinuity; everywhere else it's an open-loop system. Dicklyon (talk) 18:45, 3 June 2012 (UTC)

An off-the-shelf on-off controller, used open-loop, is not a 'cybernetic system'; it's not even a feedback loop. This discussion started with a sentence that said, "positive feedback itself creates a disturbance". It is important to distinguish open from closed loop systems, feedback signals from external forcings, amplification from feedback control, equilibria from setpoints or references, open loop transfer functions from closed loop transfer functions. In short, this is a complicated subject and necessarily has its own vocabulary. I'm all for finding references, and the section below looks very useful. --Nigelj (talk) 19:43, 3 June 2012 (UTC)

No, a bang-bang controller always runs closed loop, and can be run with positive or negative feedback (but they normally run with negative feedback). In absolutely every case, in feedback theory positive feedback is simply negative feedback with the opposite sign. GliderMaven (talk) 20:10, 3 June 2012 (UTC)

Perhaps a bang-bang controller with positive feedback, if such exists, would be better called a "bang controller". In any case, this sort of non-differentiable special case confuses the issue more than clarifying it. Dicklyon (talk) 21:07, 3 June 2012 (UTC)

Yes, you do seem quite confused. It's perfectly differentiable if you put a short slope in the middle, and it behaves in very much the same way.GliderMaven (talk) 21:38, 3 June 2012 (UTC)

The first sentence that you keep revert warring back implicitly assumes linearity. I'm completely certain that non linear positive feedback systems are quite common in nature, economics and electronics (e.g. the humble flip flop.)GliderMaven (talk) 21:38, 3 June 2012 (UTC)

I'd like to know why you think linear systems are the only ones worth considering.GliderMaven (talk) 21:38, 3 June 2012 (UTC)

I'm not sure why you think I'm focused on linear systems only. You do need differentiability (a local linearization) to distinguish between positive and negative, which is why I said above "If you take a smoothed version of your function, you'll see a region near zero where it tends to amplify disturbances; and when it goes flat, there's no longer any positive feedback there." Dicklyon (talk) 01:03, 4 June 2012 (UTC)

It's positive feedback because the amplitude is still increasing away from the reference point, pushed away by the feedback loop, which is actively returning a value to move it. There's absolutely no negative feedback to cancel it out even slightly. If by some chance the loop happened to return zero it would stop, if it returned a negative value it would move backwards towards the reference, and would then be in negative feedback. And it does this symmetrically, either side of the reference.GliderMaven (talk) 13:22, 4 June 2012 (UTC)

I've also thought of a much, much more common example, one in every computer and cell phone.

In an oscillator you want the oscillator to self start and then oscillate with a particular amplitude. The way this is usually done is to start the oscillator with positive feedback, so that any noise kicks it off and the amplitude then rapidly grows. To stop it growing the system is that the loop gain eventually rolls off and becomes below one; usually due to a non linearity.

But there's a point where the amplitude is still growing, it's still in positive feedback, and isn't yet in negative feedback, but the loop gain is decreasing. If you think about it, that means that a small perturbation gives negative relative growth, while the overall gain is still positive, the relative gain is downwards.

Now according to your 'definition' of positive feedback, that's no longer 'positive feedback'. But if it's still growing it's certainly not in net negative feedback. Negative feedback is defined as the loop returning a negative value relative to its position, but here the loop is returning a positive value, it's still growing, just at a slowing rate.

I agree that you could consider this to be a case of negative feedback towards the target amplitude, but I think that's actually a different way of designing stable oscillators, by designing a negative feedback loop to make it do that. The actual real loop here is exhibiting overall positive feedback relative to the reference that it uses, which is the zero voltage, but there's some negative feedback growing to eventually cancel it out.

I think that defining positive feedback and negative feedback in relative terms for perturbations is quite different to how it is usually considered, and it's not how the negative feedback article defines it right now, for example, either. And I think you'll find very few references for that.

By talking about perturbations, you've differentiated and you are getting slightly the wrong answer. The difference between negative and positive feedback isn't about infinitesimal perturbations, it's about real world, macroscopic, voltages or other non microscopic quantities that can move real world, macroscopic, objects. If the voltage moves the system towards the reference it's negative feedback, if it moves it away, positive feedback.GliderMaven (talk) 13:22, 4 June 2012 (UTC)

What's the "reference" in your oscillator example? Dicklyon (talk) 17:50, 4 June 2012 (UTC)

In the example I gave, it's zero volts, the oscillator initially exhibits positive feedback away from 0 volts. (Actually, if you're being really precise, for an oscillator, there's two forms of storage coupled in quadrature, and it's zero for both).GliderMaven (talk) 21:32, 4 June 2012 (UTC)

There seem two basic ways of defining the type of feedback - the mechanism or the effect. The Mindell text mentioned below describes this dispute. For technical use in human-designed systems, knowing the mechanism is necessary - I think this is where Dicklyon is coming from. On the other hand, for natural systems and simplicity of explanation, defining the differences by the observable effect is more generic. It's an old dispute. --Trevithj (talk) 19:54, 4 June 2012 (UTC)

You're saying that whenever you see exponential growth that's, by definition, positive feedback in natural systems? GliderMaven (talk) 21:32, 4 June 2012 (UTC)

Not quite. I'm saying whenever we see exponential growth due to feedback, that's by definition positive feedback. --Trevithj (talk) 06:59, 5 June 2012 (UTC)

Although... I haven't been able to think of a case of exponential growth in natural systems that isn't positive feedback. New rate-of-growth depends on present value. New value depends on present rate-of-growth. Feedback? --Trevithj (talk) 21:31, 5 June 2012 (UTC)

In the general case, feedback is heavily non linear, and negative feedback can give you exponential growth over some region of the phase space if it's sufficiently non linear.GliderMaven (talk) 22:57, 5 June 2012 (UTC)

Does that mean that in the general case, positive feedback is sometimes negative feedback? Remember we are talking about definitions here - if the growth is away from the reference point then it is "positive" by (cited) definition. If the growth is due to feedback, then it is positive feedback.--Trevithj (talk) 01:03, 6 June 2012 (UTC)

No, I mean that the behavior will be exponential growth towards the reference point. So it's still negative feedback, but giving exponential growth over some region. But it can't continue past the reference point and remain negative feedback. Mathematically, positive feedback could continue exponential growth away from the reference indefinitely, but in the real world something always eventually gets in the way. Feedback always has an input/reference and the behavior is relative to that.GliderMaven (talk) 02:08, 6 June 2012 (UTC)

OK, the following is a possible example of a non linear positive feedback open loop response, that is differentiable at all points and has negative response to perturbations over much of the response curve (the bit after the peak of the curve):

--Does this example contain only one feedback loop? --Trevithj (talk) 01:03, 6 June 2012 (UTC)

Yes. This is the open loop response of a non linear positive feedback loop. And it has the property that past the peak, a positive perturbation reduces the size of the feedback response, and vice versa, a negative perturbation increases it, while still being unstable and pushing away from the reference at all points and giving positive feedback. So neighbouring values converge to each other, while diverging from the reference. You could (for example) build an oscillator with it, although it would give you a somewhat wonky waveform, and it wouldn't be sinusoidal. Actually, come to think of it, there are people that literally do that (it's the response of an induction motor, and people sometimes build electromechanical oscillators using them.)GliderMaven (talk) 01:56, 6 June 2012 (UTC)

Since this is a possible non linear positive feedback function, the first sentence is clearly false. Given that the first sentence in the article has not a reference for it, I will remove it in a few days, unless it can be specifically referenced.GliderMaven (talk) 00:10, 6 June 2012 (UTC)

If something with this open-loop response was built into a feedback loop with the sense set to demonstrate positive feedback, the positive feedback would only exist in the relatively linear region between the peaks. Exactly at either peak, the gain of the overall system would have decreased to zero (0 x anything == 0, and the slope here is zero). Beyond each peak, what was positive feedback in the middle region would have been transformed into negative feedback by the reversed slopes. This is exactly how many positive feedback systems remain whole and so don't destroy the Earth by using up infinite energy: the effective positive feedback gain drops away to zero and then negative feedback effects come to predominate beyond that. If a feedback system was connected up using this device so that the middle region was part of a negative feedback system, the region beyond the peaks would represent a dangerous positive feedback region, or latching trap, into which the system probably mustn't stray. That reminds me of controlling devices that display negative resistance, such as tunnel diodes. --Nigelj (talk) 20:19, 8 June 2012 (UTC)

Careful here. Positive feedback is simply a feedback loop with the opposite sense feedback to negative feedback. GliderMaven (talk) 21:50, 8 June 2012 (UTC)

Recall that a feedback loop is: "information about the gap between the actual level and the reference level of a system parameter which is used to alter the gap in some way". It's nothing to do with perturbations, it's to do with the gap. That graph is a perfectly proper transfer function for a positive or negative feedback loop because it only crosses the x axis at the origin. GliderMaven (talk) 21:50, 8 June 2012 (UTC)

Again, I don't recall, and you're not saying who you're quoting. Feedback systems that I have designed, analyzed, and worked on have not usually had any "gap" in their conceptual design or their realization. As for "Positive feedback is simply a feedback loop with the opposite sense feedback to negative feedback," that may be OK, but it's still the case that some loops make positive feedback in some parts of their phase space and negative in other parts. Dicklyon (talk) 03:43, 9 June 2012 (UTC)

I think GliderMaven is quoting Ramaprasad, but I am intrigued - how is it possible to design and implement a feedback system without some measure between actual and reference value somewhere? (See eg. the Carver & Scheier quote below) How do you know if the feedback is working? I assume you are NOT talking about systems with multiple feedback loops. --Trevithj (talk) 05:35, 9 June 2012 (UTC)

Sources and definitions

It's hard to find sources that give good concise and general definitions for positive feedback, as it's such a broad term with many nuances in different fields. So let's try to collect here a few good sources, and maybe we can state a couple of definitions that illustrate the use in different areas. Dicklyon (talk) 18:08, 3 June 2012 (UTC)

• I like this discussion on the origins in electrical engineering:. It discusses even the early days the confusion between positive feedback and instability, and different interpretations of the feedback concept. Dicklyon (talk) 18:08, 3 June 2012 (UTC)

• The Federal Standard 1037C definition is completely worthless. Dicklyon (talk) 18:55, 3 June 2012 (UTC)

• Electronics dictionaries about talk about the signal fed back to the input being in phase with the input, so as to increase the gain; here are the snippets: positive feedback Feedback in which the signal returned to the earlier stage of the amplifier is in phase with and ..., With positive feedback, the signal fed back is in phase with the input and increases amplification, but may cause oscillation. With negative feedback, the signal is 180° out of phase with the input and decreases amplification but ..., Regenerative feedback : Positive feedback. Feedback from the output of an amplifier to the input such that the feedback signal is in phase with the input signal. Used to produce oscillation.; from this search. Dicklyon (talk) 19:00, 3 June 2012 (UTC)

• The World Book Dictionary says "feedback in which the output of a process is returned to its input in such a way that the effect of the process is augmented." A Dictionary of Ethology says "Positive feedback obtains when the output of the system adds to its cause, resulting in progressive buildup of output." Soil and environmental science dictionary says "There are two types of feedback: negative feedback, in which the effect of the change is to counteract the impact of the initial alteration, and positive feedback, when the effect of the change is to cause the system to continue changing in the same direction...". Please see the sources for more complete context.

• Most other dictionaries that I looked at have definitions that are too malformed to be interpretable, or too narrow, or whatever. But I haven't been able to find ANY that mention equilibrium in connection with positive feedback, though some, like the Encyclopedic Dictionary of Archaeology, speak of equilibrium with respect to negative feedback, and contrast that with positive feedback; this one says "deviation-amplifying system: A system that continues to change as a result of positive feedback. / deviation-counteracting system: A system that reaches equilibrium as a result of negative feedback." Dicklyon (talk) 19:15, 3 June 2012 (UTC)

John Sterman offers a simple definiton in Business dynamics: "Positive feedback denotes a self-reinforcing process..." He also describes an example possibly relevant to this discussion:

"Imagine a ball balanced on top of a hill. As long as the ball is exactly balanced... it remains in equilibrium. But the slightest breeze pushes the ball down the hill ever so slightly, leading to a still greater force downhill, in a positive feedback. The equilibrium is unstable."(p130)

There is also Carver & Scheier's definition, and Ramaprasad's too, both cited already in the above discussion. On the subject of reference values, Carver & Scheier also go on to say:

"The [feedback] loop has two sources of information, the input function and the reference value. It should be apparent that both sources are important - indeed, both are necessary for a feedback loop to exist and to function."

Defining "positive" (in the sense of "increasing") requires a reference value. --Trevithj (talk) 08:26, 4 June 2012 (UTC)

I scored a copy of Harold Chestnut and Robert W. Mayer's Servomechanism and regulating system design volumes I & II (1955). While they don't use the terms 'positive feedback' or 'negative feedback' but on page 311 of volume I, they do cover the "degenerative feedback" which is self evidently negative feedback and "regenerative feedback" which is clearly positive feedback; well the diagram is the same as positive feedback with control element G1 and feedback element H and regenerative feedback is defined as:

"in which the output is fed back with positive sign as shown in 10.2-14" and then they show the normal positive feedback diagram, with an input labelled I. Elsewhere for negative feedback circuits there's a minus on the adder blob and the input is labelled as 'reference' but otherwise it's the same diagram. They also talk about using regenerative feedback to build oscillators (where the effective gain is infinite, you put in no signal and get a signal out.)

I've also got a copy of Electronics Circuits and Devices (second edition) Ralph J.Smith (1980) which talks about combining positive and negative feedback to build stable oscillators. Pg 417 talks about "positive feedback in an oscillator circuit", in the case they talk about they use the non linear response of an incandescent lamp in a negative feedback to control the amplitude.

On page 416 they do give what seems to be a definition of positive feedback though, at least for a complex linear system, they say:

"For GH positive but less than unity, the denominator is less than unity and the system gain is greater than the forward gain G. This condition of positive feedback was used in regenerative receivers to provide high gain in the days when electronic amplifiers were poor and signals were weak. Operation with positive feedback becomes less stable as GH approaches unity, so regenerative receivers required constant adjustment. If the value of GH approaches 1+j0, the demominator approacehes zero and the overall gain increases without limit." And then they talk about oscillators which deliberately use that.GliderMaven (talk) 23:31, 4 June 2012 (UTC)

It's a little bit ambiguous, you can read that as positive feedback is when the gain is less than one, or that 'positive feedback' holds the whole time the feedback is applied in the positive sense. I'm thinking that the second is true though, it's more logical from a naming point of view, and they never actually say that positive feedback no longer exists when you reach the oscillation point.GliderMaven (talk) 23:31, 4 June 2012 (UTC)

I believe that's right, that it's positive feedback whether more or less than unity magnitude. Dicklyon (talk) 04:41, 5 June 2012 (UTC)

From the area of Service Improvement and performance feedback:

In sum, the effect of performance feedback on task performance has been explained using three different theories. Behavioral theory stresses the importance of feedback as external reinforcer/punisher or as cueing stimuli. Control theory emphasizes the error correction or informational nature of feedback. Social cognitive theory explains the feedback performance link through the detailed mediation of cognitive processes such as goals and self efficacy.

Article's present emphasis is on 2nd (control) theory. --Trevithj (talk) 21:42, 5 June 2012 (UTC)

GliderMaven, regards the edited "ideal feedback model" text - does the new referenced text refer to an "ideal feedback model"? If not, I think you have invalidated the diagram. --Trevithj (talk) 01:06, 6 June 2012 (UTC)

There's a figure 14.2 on page 414 which is exactly the same and the surrounding text calculate the gain while specifying that the boxes are linear for that particular calculation (they do that mostly because calculating gain for non linear boxes would be very tricky, and many, but not all, amplifier circuits are approximately linear).GliderMaven (talk) 02:19, 6 June 2012 (UTC)

It's not the figure so much as the caption. If the caption calls the figure an "ideal block diagram", that is a fairly grand claim and needs to be cited. Could you change the description to whatever your cited text uses? To keep things consistent. --Trevithj (talk) 02:45, 6 June 2012 (UTC)

I made some adjustments there that I hope will meet with approval. The reason for the linear system diagram is that it is an "idealization" of a real situation, not that it is "ideal". That is, it's simplified to be easy to analyze. I added a ref that discusses a similar diagram, in terms of disturbances and effects, much like (but not exactly like) our lead sentence. I'm not claiming we have the best definition, but it is at least pretty much supportable by this source (with some possible quibbles about what's a perturbation and what's an effect). Dicklyon (talk) 05:27, 6 June 2012 (UTC)

To clarify, the diagram has been over-used in the past IMO. The citation that GliderMaven removed (Chen 1991) is the only one I could find that actually referred to this diagram as an "ideal feedback model". I'd be in favour of replacing the diagram with something more relevant to PF - this one seems to be based on the Negative feedback amplifier diagram from Harold Black's work. But I'm okay with your changes if they match the cited text. --Trevithj (talk) 01:45, 8 June 2012 (UTC)

Broadcast storm paragraph

As part of a copyedit of the Positive feedback#In electronics section, I have removed the following paragraph from its end. It was added relatively recently, and initially I was going to tidy it up. On careful reading, however, and looking at the broadcast storm and switching loop articles, I'm not sure that it's really an example of positive feedback. It sounds more like the kind of cascade effect that goes on in a nuclear chain reaction, which I don't think really represents actual feedback.

In networking, a form of positive feedback known as a broadcast storm can result when multiple switches are connected in such a way that they form a loop. Say for example, you have two switches, each with 4 ports. By accident, ports 1 and 2 are connected to the other switches ports 1 and 2. A single multi-cast packet is sent, switch one receives it, and sends it out through every port besides the one it came in on. Switch 2 receives 2 multi-casts, and sends each of them out on every port besides the ones they came in on. Switch 1 then receives 2 again, and the process repeats. This begins flooding the network with packets being rapidly bounced back and forth until the entire network is crippled.

What do others think? We could sort out all the 1's and 2's if necessary. --Nigelj (talk) 22:04, 7 June 2012 (UTC)

I would say it's not a very good example of positive feedback, and is not of the sort meant by "electronic" in any case. Dicklyon (talk) 00:23, 8 June 2012 (UTC)

It fits PF in the broadest sense - any two elements that influence each other in a self-reinforcing way. But the electronic sense is usually much more specific around mechanism. Also, it isn't the easiest example to follow (unnecessarily detailed IMO). It would be okay if summarised and put in a different section. With that in mind...

Could the Electronics section be sub-divided (e.g., Amplifiers/Controllers/Networks) to allow a more detailed treatment of each area? Especially Amplifiers - this is historically where the term "positive feedback" came from, after all (Friis and Jensen, 1924) but it can get quite difficult for the non-technical reader. --Trevithj (talk) 01:00, 8 June 2012 (UTC)

Entire first paragraph oversimplifies positive feedback

The problem is that positive feedback in most systems is symmetric- when the system state is above the equilibrium/reference/input/whatever you want to call it the system state grows upwards, that's the obvious bit that everyone knows, but when it's below the equilibrium point, it grows downwards. That's the bit that people don't seem to be getting.

The fact it can go in either direction is critical, particularly in things like hysteresis. Hysteresis is a common design feature based around positive feedback.

With hysteresis, when the system state is above the input, the system runs away from the input, until it mashes up against a hard limit. But if the input then goes above that limit, the positive feedback direction flips, and then suddenly forces the system to race down towards a lower hard limit. That's how light switches work, thermostats, also door catches, ratcheting pens and so on.

The fact that positive feedback pushes symmetrically (or asymmetrically) away from the input, is actually the whole point; that's the definition of positive feedback not that it always grows every little perturbation. If you read the negative feedback article and consider that positive feedback is the exact opposite of negative feedback then this should be a bit clearer.

The other thing is that positive feedback doesn't characteristically grow exponentially; in some cases it will, but that's not a firm characteristic. In the case of mechanical hysteresis, the positive feedback is often provided by a spring, that will often cause quadratic growth or similar, and actually you can design the growth curve you want into most human built systems by changing the mechanism's spring rate and leverage and so on.GliderMaven (talk) 00:08, 8 June 2012 (UTC)

I agree about the usual symmetry, but you're still too focused on the the behaviour around an unstable equilibrium. Positive feedback is also common in stable systems, oscillating systems, etc. The idea of increasing or amplifying perturbations is common to all these cases. As for the springs and quadratics, I have no idea what you're referring to. Refs? Dicklyon (talk) 00:27, 8 June 2012 (UTC)

The idea of increasing or amplifying perturbations is common to all these cases. There is a strong possibility for confusion with the idea of increasing or amplifying values. If we're using numerical measures, then the first is an absolute value, the second is the more commonly understood idea of a real number > 0. It wouldn't hurt to clarify this ambiguity for the non-technical reader. Especially considering that we use the second usage when referring to loop gain. --Trevithj (talk) 01:15, 8 June 2012 (UTC)

How are you using the term 'perturbation' here? A perturbation is, by definition, a very small value, a small change, usually due to a noise of some kind. For example the output of a system at a particular time might be at 3.2 volts and the input might be 0 volts. An input perturbation might be 0.001 volts pushing it up to 3.201 v. If the system output exponentially grows by (say) 10% in one second to 3.521-odd volts due to feedback, then is it the 0.001 volts perturbation as opposed to the 3.2 voltage growing? In my book, the 3.2 volts is not a perturbation, and the growth of the perturbation makes very little difference indeed to the system behavior. And that's a pretty general feature of these kinds of circuits. Only when the system is very close to a tipping point will perturbations make any appreciable difference. Usually they make no significant difference at all. So how are you using the term 'perturbation' is it the 0.001 volts or the 3.2 volts or something different? GliderMaven (talk) 02:05, 8 June 2012 (UTC)

How are you using the term 'small' here? --Trevithj (talk) 02:24, 8 June 2012 (UTC)

Close to zero. Perturbations are close to zero.GliderMaven (talk) 02:43, 8 June 2012 (UTC)

Okay ... define 'close'. Why is 0.001 close, but 3.2 (or 32 or 320) not close? Trevithj (talk) 09:10, 8 June 2012 (UTC)

Two examples of mechanical positive FB are, the inverted pendulum that I've used a couple of times above, and the over-centre action mentioned in the lede. Examples of over-centre actions are locking pliers, those dish-shaped bimetal things in thermostats that click, light switches that snap on or off, and the human elbow when you lock it to lean on something. The trouble with saying "Only when the system is very close to a tipping point will perturbations make any appreciable difference" is that it is only when close to a tipping point does positive feedback exist or predominate in most of these. The reason that perturbations make no appreciable difference when the thing is either latched or unlatched is because it has then entered a non-linear or low-gain state where extraneous limiting forces have applied enough negative feedback to swamp the positive feedback and bring the system to a standstill (with or without damage). In an electronic flip-flop, perturbations on the input that put it into the present state will not move it. Once mole-grips are locked, you can hit the thing with a hammer and they won't (usually) unlock. Once an inverted pendulum has hit some end-stops at ±90°, or has swung right down to 180°, it will withstand all kinds of perturbation without showing +ve FB. The linear region just around the tipping point is where you will see positive feedback; outside of that, negative feedbacks and non-linearities take over and the system may become quite stable or quite broken.

If I had to define the size of a suitable 'perturbation', I'd say an alteration that is large enough to have a noticeable effect, without introducing immediate side-effects or breaking the system. Something that provides a perturbation on a spider's web will have no effect on a gun turret, and vice versa you'll break it. If you want to start an animal stampede, you spook one or two animals. If you destroy them all at once with a large bomb, you won't see a stampede.

Way back above I really tried to imagine a perturbation towards equilibrium on a +ve FB system, acting in its linear region (i.e. the region where a working +ve FB mechanism actually exists). I came up with a thin thread resisting an inverted pendulum after it has moved away from 0°, then breaking. Even further back above I came up with an inverted pendulum 'tamed' by two fairly light tension-springs that were capable of applying some negative feedback to the positive feedback system and making it oscillate under the right conditions. Really the snapping thread is just a momentary bit of negative feedback built into the system, and I don't think it's a 'perturbation' at all. The actual perturbation is whatever took the pendulum away from 0°, its unstable equilibrium point. That was an input. --Nigelj (talk) 19:41, 8 June 2012 (UTC)

It sounds like perturbation is being used here to distinguish between a triggering effect and a resultant increasing change. While I would have thought that an external effect of temporary duration would be more relevant to the definition of perturbation myself, rather than magnitude (a bomb would perturb a herd of cattle!) I must admit the distinction seems a useful one to make. Is it feasible to use perturbation in this sense consistently through the article? --Trevithj (talk) 05:26, 9 June 2012 (UTC)

Regards the first sentences in both the Lead and in Terminology sections: can someone double-check the definition used in the cited source? [3] It seems to me that the book's definition of "positive" refers to "process gain", and only incidentally suggests that the gain may be proportional to the output (and so due to feedback). This is confusing, and not strictly compatible with the article text "'positive' refers to the mathematical sign of the loop gain." "Loop gain" is never mentioned.

Also, the statement "the effects of a small disturbance on a system include an increase in the magnitude of the perturbation" doesn't appear to be anywhere in this text - nor anything like it. "Perturbation" only appears twice in the book, and "disturbance" doesn't appear at all.

This book may be too domain-specific to make a good generic citation. Thoughts? --Trevithj (talk) 06:46, 9 June 2012 (UTC)

Rather than take up more room here with a lengthy proposal, I've put up some cases on my talk page, gleaned from my recent reading on "feedback" and intended as a guide to definitions. --Trevithj (talk) 00:33, 12 June 2012 (UTC)

Nah. We discuss this article here, not on your talk page.GliderMaven (talk) 00:08, 15 June 2012 (UTC)

Yes, dad. --Trevithj (talk) 03:01, 15 June 2012 (UTC)

For example "That is, A produces more of B which in turn produces more of A." to me implies that positive feedback always causes growth, but it also causes collapse. For example if you have a bank account, the balance is clearly subject to positive feedback, if you have money in it, you get compound interest. But if you owe money, you get positive feedback in the opposite direction towards owing more. The latter is not an example of negative feedback. And note that it's nonlinear; you get different APRs depending on whether you owe or are in credit, and the feedback is episodic, you get fined for getting overdrawn, and the positive feedback from the interest is episodically applied once a year. Positive feedback is not of necessity a continuous process, it's not about perturbations, it's only about whether you're in credit or in debit, it's about being pushed away from the equilibrium point (in this case zero money in the account.)GliderMaven (talk) 00:29, 15 June 2012 (UTC)

How about using the VHS/Beta videotape format war example instead for the lede? Positive feedback drove VHS's sales up and Beta's sales down. Same process, both directions. There was some material by Brian Arthur that covered this. Hmm...

I just searched Google scholar for "Positive feedback" VHS Betamax and got some pretty good readings.--Trevithj (talk) 03:01, 15 June 2012 (UTC)

Yes, that story is well told in Gleick's book Chaos. The network effect provides positive feedback. But I think it's a bit too much of a stretch to get people to understand and appreciate it. It took Arthur years to get his theory to break through the dominant paradigm, not because people didn't know what positive feedback was, but because they weren't used to applying it in economics of scale. Dicklyon (talk) 03:17, 15 June 2012 (UTC)

Growth and collapse are not the right concepts here, especially if you look at a linear approximation. Growth can be in the positive or negative direction, and growth is what you get if there's enough positive feedback for the system to be unstable. In general, disturbances up or down will be amplified. "Collapse" is relevent only in strongly nonlinear systems, where a downward growth is constrained by some kind of a floor. Dicklyon (talk) 04:55, 15 June 2012 (UTC)

The point is not the word 'collapse' the point is that the introduction is grossly misleading, since positive feedback commonly causes exponential reduction as well as exponential increases. Why do you keep downplaying this point when it's central to what positive feedback is? This topic is as related to negative feedback and feedback loops as it is possible to be, and yet this article introduction seems to be deliberately written to obscure this point, whereas they both adequately describe their topics.

Not to put too much of a fine point on it, the entire first paragraph is completely and totally god-awful. The first sentence is factually false. The second sentence implies that positive feedback gives only growth, but in reality positive feedback equally causes reductions in output. The third sentence misrepresents negative feedback. I don't have access to the 'sources' cited, but it's totally clear that they're lightweight, fluffy, unreliable sources for the claims made for them.

I don't think it's possible for anyone who didn't know the topic before hand to read that paragraph, and to not get completely wrong idea about what positive feedback is. It is the worst introductory paragraph I have ever seen in Wikipedia, by a very, very, very long wayGliderMaven (talk) 12:30, 15 June 2012 (UTC)

Now that's a good example of hyperbolic... but seriously, exponential decay is a property of stable linear systems in general, with positive or negative feedback, or none. It's not clear what concept you're going for here. What source can we consult that does it your way? Dicklyon (talk) 15:27, 15 June 2012 (UTC)

I'm not being hyperbolic, that first paragraph is a load of old crap. I'm very familiar with (and had formal training in) positive feedback in electronics, and that first paragraph doesn't cover positive feedback in electronics properly (even).GliderMaven (talk) 18:05, 15 June 2012 (UTC)

Positive feedback is simply a particular type of feedback that occurs when you have a feedback loop (either natural or engineered)! It's NOT: "a process in which the effects of a small disturbance on a system include an increase in the magnitude of the perturbation"; that isn't positive feedback. Positive feedback can sometimes have that effect, but it needn't. By writing it like this, you're saying that the article is only covering part of the topic of positive feedback. The first few sentences of an article in Wikipedia is supposed to be an overarching definition that is always true.GliderMaven (talk) 18:05, 15 June 2012 (UTC)

The definition of positive feedback is that it is a feedback loop has an overall positive sign on its feedback loop gain. That's all it is. That's why it's called 'positive feedback', strangely enough.GliderMaven (talk) 18:05, 15 June 2012 (UTC)

It is NOT defined as having positive perturbation gain, it is NOT defined as always growing exponentially in magnitude, it is NOT defined as being unstable, it is not defined as being linear, it is not defined as being monotonic, it is not defined in many, many other ways that are equally wrong. The definition is that a system has positive feedback iff the loop gain > 0. Always. That's it, that's all. The perturbation can be negative or zero, it can be unstable or stable, it can be linear or nonlinear, the gain can be monotonic or non monotonic, provided it has positive overall gain.GliderMaven (talk) 18:05, 15 June 2012 (UTC)

Well, you have now added four tags to the opening paragraph and are starting to post your comments in bold type. Everyone here has disagreed so far and we have regularly asked you for sources for what you are saying. I think you need to provide a link to citable source that supports your opinions. --Nigelj (talk) 20:11, 15 June 2012 (UTC)

Glider, you're complaining that it's oversimplified, and providing another oversimplification as an alternative. And have you even proposed that definition in the section on definitions and sources? I think you noted that it's hard to talk about the loop gain when the system is not linear, which is true; it can also change with frequency in a linear system. So this "overall" gain you refer to remains an undefined over-simplification. Why would this be better than the description we have now? Dicklyon (talk) 20:36, 15 June 2012 (UTC)

I can't understand how you can really think this is hard. Loop gain is simply the feedback value/summed value, if that is positive then you have positive feedback, if it's negative you have negative feedback. It doesn't matter if it's nonlinear or not. In my opinion, if you really do think this is hard you definitely shouldn't be editing this article. If you don't think this is hard then presumably you're being dishonest with us, and you shouldn't be editing this article. Either way, I don't understand what you're doing here. Every time you guys post something on this topic, I facepalm some more.GliderMaven (talk) 22:56, 15 June 2012 (UTC)

Another use of positive feedback is described here: here where they design Schmidt triggers and latches and oscillators using opamps. They simply connect the output to the positive summing input.GliderMaven (talk) 22:56, 15 June 2012 (UTC)

None of these systems described there are defined by "the effects of a small disturbance on a system include an increase in the magnitude of the perturbation"; these and all positive feedback systems are simply defined by the sign of the feedback. Is this all some kind of joke? Please tell me you guys are just joking!GliderMaven (talk) 22:56, 15 June 2012 (UTC)

What's hard is understanding you, and finding a good definition. What, for instance, are the values referred to in your "feedback value/summed value"? I'm not just joking, but trying to understand how you decide what is "the sign of the feedback" in the general case. Dicklyon (talk) 23:08, 15 June 2012 (UTC)

Look, take the basic feedback diagram:

Basic feedback diagram

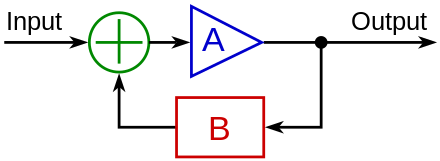
As you can see, the input (which in some circuits/systems is held at zero, in others at some other value, for example a digital clock, like in a computer would be "biased" at half the system voltage. Then there's a process block A, which can be an arbitrarily complex function of the input, and then there's another feedback block B which can be an arbitrarily complex function also, and both can be positive or negative. Both A and B can contain clamps, and positive and negative going functions. They would be differentiable, but that's about all.GliderMaven (talk)

The other thing about the blocks is that they necessarily have a slight temporal delay through them.GliderMaven (talk) 00:30, 16 June 2012 (UTC)

In positive feedback the output after going through the second block will have the same sign as the output of the adder. In that case, for as long as that is happening, the output of the adder will be pushed away from the input value. This is termed 'positive feedback'. If the output is negative, it will be pushed towards zero. This is termed 'negative feedback'. It's nothing to do with perturbations, per se, it's simply the sign of the feedback.GliderMaven (talk) 00:30, 16 June 2012 (UTC)

This diagram models bank accounts, schmidt triggers, oscillators, amplifiers and much more. Some more complex feedback systems have many more inputs and outputs, and more states; this one only has one state, which is the 'output'.GliderMaven (talk) 00:30, 16 June 2012 (UTC)

A more complex example would be a predator-prey relationship, for example gazelles and lion populations, and one or more inputs, such as the amount of food for gazelles. The number of gazelles would have a positive feedback effect on the number of lions (because they feed the lions), and the number of lions would have a negative feedback effect on the number of gazelles (because they eat them).GliderMaven (talk) 00:30, 16 June 2012 (UTC)

So it's a very general concept. Obviously, that diagram is too basic to handle two or more outputs, but it's easy to make similar diagrams with more outputs and you should be able to begin to see the gap between the article and the reality of positive and negative feedback loops.GliderMaven (talk) 00:30, 16 June 2012 (UTC)

The lead text is just wrong, and I just checked and it has been wrong for years.GliderMaven (talk) 00:30, 16 June 2012 (UTC)

The sign at the output of the adder is irrelevant, as it can be arbitrarily messed with by transients in the input. What's key is the sign of A*B, which depends on frequency in a linear system, and on other stuff in a nonlinear system. That's why some of the book defs that I cited use the concept of "in phase with", since that implicitly picks out a frequency range in the input and the feedback; I believe it means that the dot product or direction cosine of the input and the feedback is positive, since it won't usually be exactly in phase. Anyway, the effect of that is as described in the lead, to amplify the effect of disturbances. Do you have a definition that's sourced and improves on that? Dicklyon (talk) 01:53, 16 June 2012 (UTC)

It's in no way irrelevant, if there's a momentary change (a transient) of the input that generates an opposite value (or opposite phase) to the feedback loop value then that would be negative feedback, not positive feedback!!! Right? Similarly (and more problematic) if the system is in negative feedback and the transient momentarily generates a positive gain, then it's positive feedback, and if the transients are maintained, and the gain is sufficiently high then it will oscillate. That's how it works!GliderMaven (talk) 19:35, 16 June 2012 (UTC)

Your definition based on the sign of the loop gain is not bad, though it's poorly supported by the cited source, which says it when g is positive, ignoring the signs of the other transfer functions. Your analysis of the transient ignores the transient nature of it; the sign after the adder will change before the sign of the feedback does; that doesn't mean it's negative feedback for transients. Dicklyon (talk) 21:58, 16 June 2012 (UTC)

The trouble I find when looking for a source to support positive loop gain meaning positive feedback is that so many sources, esp. in control theory, define the loop gain the other way around, as positive for negative feedback. Dicklyon (talk) 22:17, 16 June 2012 (UTC)

Regards an overarching definition that is always true: see definitions from a variety of published sources (with context). References available if required.

• "The positive feedback loop produces exponential departure from some reference or neutral condition..." (systems dynamics)
• "...positive feedback is characterized by the fact that changes create a tendency to new changes in the same direction." (law)
• "Positive feedback is an escalating flow of information which results from an exchange of ideas..." (management)
• "...a positive feedback loop is self-reinforcing; the more it works, the more it will continue to induce change." (systems dynamics)
• "[a process whereby] a change in one direction sets in motion reinforcing pressures that produce further change in the same direction." (politics)
• "Positive feedback is defined as a recursive process whose inputs are a positive function of its outputs." (psychology)
• "Feedback is defined by mutual influences between two elements, such that if A influences B, B also influences A. Positive feedback is defined as an element exerting an influence that amplifies a prior deviation." (psychology)
• "Positive feedback is defined as a process whereby it becomes increasingly difficult to reverse course as time goes by." (politics)
• "Positive feedback is defined as appreciation of good performance for one's work behavior..." (management)
• "Positive feedback is defined as enhancing the process..." (systems dynamics)
• "[Positive feedback is a] self-reinforcing mechanism that accentuates rather than counterbalances a trend..." (politics)
• "[Positive feedback is] the enhancing or amplification of an effect by its own influence on the process which gives rise to it." (politics)
• "Positive feedback increases the gain of the amplifier..." (electronics)
• "[With positive feedback] the action triggerd by feedback widens the gap between the reference and actual levels of the system parameter." (management)

The underlying problem with this article may be that there isn't a commonly-agreed definition, even within a given discipline. --Trevithj (talk) 08:19, 16 June 2012 (UTC)

I think GliderMaven is arguing either for a definition based on how you make a positive feedback system ("They simply connect the output to the positive summing input") or one based on describing one mathematical model of a positive feedback system ("Loop gain is simply the feedback value/summed value, if that is positive then you have positive feedback"). Our definition is based on how you would recognise a positive feedback system. It seems well enough supported by the list of definitions, commentaries and descriptions Trevithj has diligently sought out above ("amplifies a prior deviation", "will continue to induce change", "enhancing or amplification of an effect" etc). What's important to understand is that there doesn't have to be a perturbation for positive feedback to exist, and that the perturbation, if there is one, is not part of the positive feedback mechanism. It is just that if there were to be a perturbation then positive feedback would do what we say it would. But really, per WP:TPG, if there is a better definition proposed, let's see what it is in actual words - state it here in quotes. And provide the list of citable sources that say that's what it is. Enough of this hand-waving. --Nigelj (talk) 16:56, 16 June 2012 (UTC)

No! I'm not arguing for "how you make a positive feedback system," I'm saying that something is a positive feedback loop when there is a feedback loop and the loop gain is positive. It doesn't matter whether it's a natural feedback loop or an engineered feedback loop. Many positive feedback loops occur in biological or physical systems. That's how you recognize it, that's what a positive feedback loop IS. There's no ifs buts or maybes. That what it is.

It's not some vague thing that grows in any particular way due to perturbations or whatever, it's not every situation in which increasing something increases something else, which increases the first thing; it's a feedback loop iff there is a positive sign on the feedback. So if you have a feedback loop and the gain momentarily goes negative- at that moment that's no long positive feedback. If it then goes back positive, it's positive feedback again. It's a very precise, formal definition, and it's already in the article, has been for some time, and IS referenced.

Positive feedback loops, in general, is what this article is and should be about (and I don't just mean in electronics) they do all kinds of interesting, counterintuitive and crazy things, and your collective continual attempts to change the topic to become 'exponential growth' or 'explosive growth' or 'growth' or whatever are really, really annoying. I mean they do that, but they do lots and lots of other interesting things, but everyone seems to be keen to limit it to one corner for no obvious reason.

Anyway I moved the pre-existing, referenced material to the lead that already defines it this way.

For the record I'm getting really, really, really tired of this shit.GliderMaven (talk) 19:06, 16 June 2012 (UTC)

The definition of positive feedback as positive gain in a feedback loop subsumes all of the others. All of the others are, at most, SUBSETS of that. It is the most general definition possible, it's also the one that comes from feedback theory. As such it correctly scopes the article!GliderMaven (talk) 19:10, 16 June 2012 (UTC)

If you keep restricting the topic, I will have to remove material from the article, things like hysteresis and regenerative amplifiers become off-topic since they do not involve exponential growth, even though they involve positive feedback, but the topic in Wikipedia is what it says at the top of the article.GliderMaven (talk) 19:24, 16 June 2012 (UTC)

Still no suggested alternative text, and still no references. Please see WP:TPG --Nigelj (talk) 13:55, 17 June 2012 (UTC) Opps, my mistake. I see you have gone ahead and made changes to the definition in the lede without references and without consensus and without proposing any actual text here. Are you familiar with the difference between reality and a mathematical model? E.g., something falls, and Newton's law of gravity; something moves, and Newton's laws of motion. Then along comes Einstein and changes all the equations, i.e. the mathematical model, but things still fall and move in exactly the same ways and at exactly the same speeds. The mathematical models have been changed, but reality hasn't. Which is the most fundamental? Your new definition brings in a number of terms from one mathematical model to explain a piece of reality that that model tries to describe, without defining the terms or introducing the model. Within the world of the model, you are right, but that is something for later when we discuss the various models, not a good fundamental definition for the first sentence. --Nigelj (talk) 14:12, 17 June 2012 (UTC)

No, I just moved it up, it was already in the article, and already had an attached reference, but Dicklyon subsequently removed the reference.GliderMaven (talk) 16:04, 17 June 2012 (UTC)

The scope of the article determines what goes into the article. The only workable definition of positive feedback to scope this article is that it's a feedback loop with a positive sign on the loop gain. That's how it's defined in electronics, and if you define it any other way, half of electronics becomes off-topic here. That particular definition can give exponential growth, amplification, hysteresis etc. etc. everything you would consider to be positive feedback. If you use any other definition, I have to start deleting stuff. It's the most general definition there is.GliderMaven (talk) 16:04, 17 June 2012 (UTC)

That's just how it is defined. If we suddenly found that some part of reality didn't have a positive feedback loop, that's fine, it would get removed from the article, leaving perhaps a note of the history that that particular part of reality was once considered to be a positive feedback loop, but it turned out not to be. So it doesn't matter. This article is about positive feedback, not about exponential growth, for example, unless the exponential growth is caused by a positive feedback loop.GliderMaven (talk) 16:04, 17 June 2012 (UTC)

If "that's just how it is defined", and if people in every field from economics and biology to climate and social sciences have been defining positive feedback by looking at the sign of the loop gain, then you should have no trouble finding a list at least as long as the one above of definitions in those terms from papers and textbooks. But now I am going to have to warn you for the third time on this page about civility. "If you use any other definition, I have to start deleting stuff", "your collective continual attempts to change the topic to become 'exponential growth' or 'explosive growth' or 'growth' or whatever are really, really annoying." ( I don't see anyone doing that actually here), "Is this all some kind of joke?", "that first paragraph is a load of old crap"... These are not good examples of the way we discuss technical topics here on Wikipedia. You have altered the article against consensus, you have insulted your colleagues, belittled our attempts, threatened to delete and to remove text from the article willy-nilly, and have still failed to come up with general references for your proposed definition. --Nigelj (talk) 18:48, 17 June 2012 (UTC)

That is how it's defined, and I've added a reference to the sentence now, and the existing reference that was supposed to support the woolly first sentence, (which is now the second sentence) that reference "Human Population and the Environmental Crisis By Ben Zuckerman, David Jefferson" on page 42 states:

“ The mathematical description of feedback is summarized in Figure 3.1. The feedback gain, denoted by g in the figure, is a number that is positive if the feedback is positive and negative if the feedback is negative. As shown, the total effect is the product of the direct effect times the factor 1/(1-g). When g is between 0 and 1, the factor 1/(1-g) is greater than one and so positive feedback causes the total effect to exceed the direct effect. (If g is equal to or greater than one, then feedback is so strong that the system goes unstable and the foorumla above no longer applies.) When g is negative, the factor 1/(1-g) is less than one and so negative feedback causes the total effect... ”

This is extremely clear, clearly definitive and was already referenced, and was what I was already claiming, and is other than what the text I was complaining about was stating.GliderMaven (talk) 20:12, 17 June 2012 (UTC)

I like what you're doing in making the terminology more consistent. Using loop gain looks promising - so long as it is explained clearly for the non-techs. This source is saying "loop gain" = 1/(1-feedback_gain), is that right? The reason I ask is that I searched the source for the phrase "loop gain" and got no hits. --Trevithj (talk) 23:56, 17 June 2012 (UTC)

No, the correct formula is "closed loop gain" = "forward gain" / (1 - "loop gain"). But often in control systems and discussions on negative feedback, the sign of loop gain is taken to be the other way around, so positive loop gain means negative feedback, in which case the formula is "closed loop gain" = "forward gain" / (1 + "loop gain"). The first way makes more sense (to me, and is the one I was taught and have always used), but is far from being uniformly used in sources. Dicklyon (talk) 00:27, 18 June 2012 (UTC)

The trouble with the quoted passage about "g" is that it ignores the other factors, iirc. Where's the link? Does it say something to clarify what it's assuming? Dicklyon (talk) 00:30, 18 June 2012 (UTC)

Ah, here's the link. From the formula, it's clear by g has to be the loop gain, defined in the sense that I meant, and that he uses my formula "closed loop gain" = "forward gain" / (1 - "loop gain"). But he doesn't define g as the loop gain, so doesn't do a good job supporting this definition and approach. Dicklyon (talk) 00:36, 18 June 2012 (UTC)

It's clear what he means though, otherwise the maths wouldn't work out, and it matches the formula I had in the electronics book.GliderMaven (talk) 00:50, 18 June 2012 (UTC)

When we're doing Wikipedia sometimes we just have to summarise stuff, and sort out minor errors and omissions that sources may make and reword things slightly to be self consistent within the article. In this case g isn't defined, but we know what he means.GliderMaven (talk) 00:50, 18 June 2012 (UTC)

(Sigh) Going back to what I said about making it clear for the non-techs... What is the difference between "closed loop gain" and "loop gain"? And if g=loop gain, doesn't that mean we have an example here where a positive loop gain must be < 1? --Trevithj (talk) 01:22, 18 June 2012 (UTC)

Yes, that's how a regenerative feedback amplifier works, you set the loop gain just below 1 and you get a stable amplifier with enormous gain. The only problem is that if you sneeze the loop gain goes over 1 and it runs away. That amplifier type is not used much anymore. But it is an example of stable positive feedback provided you don't overdo it.GliderMaven (talk) 02:04, 18 June 2012 (UTC)

I assume you are answering my second question. If so, you maybe miss my point. It seems to me that if g=1 then the "closed loop gain" is infinity, and if g>1 then the "closed loop gain" is negative. Are we okay with this as a mathematical model? --Trevithj (talk) 02:33, 18 June 2012 (UTC)

No, no. The 1/(1-g) is the sum of the infinite geometric series: 1+g+g^2+g^3+... which converges if g<1. If g >= 1 it's divergent/infinite not negative at all (in practice you get exponential growth of the output due to the feedback delays). So the 1/(1-g) equation is only valid if g<1.GliderMaven (talk) 02:49, 18 June 2012 (UTC)

I'm not arguing against the definition, but it would sure be nice to have at least one source that explains it sensibly. It's only clear what he means by g if you infer it from the math, which means you have to either understand his derivation or know it from elsewhere. Not very satisfactory. And it certainly isn't useful to all the control people and such, for whom a positive loop gain means negative feedback. If we're going to define positive feedback in terms of loop gain, we need to explicitly define loop gain, no? Dicklyon (talk) 00:58, 18 June 2012 (UTC)

I'm "slightly" arguing against it. I think the loop gain is possibly on the right path - but for our purposes, it is the polarity of the entire loop that matters, not the polarity of one part of it (if polarity is the right word). The whole loop needs to be "positive" to count as a positive feedback loop. If for example the "forward gain" is negative, all bets are off. --Trevithj (talk) 02:33, 18 June 2012 (UTC)

Careful. If the reverse gain is negative as well, then you still have positive feedback. It's actually the product of all the gains around any given loop that matter.GliderMaven (talk) 02:49, 18 June 2012 (UTC)

Precisely my point. Does loop gain (g) contain the product of all the gains around the given loop? If not, we can't reliably use it. If so, the above definition seems to be lacking that distinction.

Dicklyon's point about control theory applies here too - seems that we need to include the "gain" of the comparison function (green circle with cross) as well as AB. --Trevithj (talk) 00:02, 19 June 2012 (UTC)

We could perhaps define it on the feedback loop page. These are examples of feedback loops after all. And I'm not sure about the control people thing, are you talking about those feedback control diagrams which have a negating input on them?GliderMaven (talk) 02:04, 18 June 2012 (UTC)

Trevithj, the "open loop gain" is from input to output when the feedback loop is opened (or cut). It's the "A" in the diagram above, or what I called the "forward gain". The "closed loop gain" in from input to output when the loop is closed (or in place as in the diagram). The "loop gain" is the gain from any point in the feedback loop back to that point, with the loop broken there, irrespective of where the input and output are; A*B in the above diagram, but in control they draw it with a minus sign instead of a plus, such that a positive loop gain means negative feedback. Look in any control book. That's also how it's typically treated in the Nyquist stability criterion, as shown in that article. So without a clarifying definition, the statement "loop gain" > 0 could mean positive feedback to some, and negative feedback to others. Other sources, like this one, use positive feedback and negative feedback to mean whether the drawing has a positive or negative sign there, and all the loop gain to be positive or negative in either case; very confusing and pointless in my opinion, but there's really no standard of whether to draw the feedback loop with a plus or a minus or to let that vary with whether you want to call it positive or negative feedback. Dicklyon (talk) 04:56, 18 June 2012 (UTC)

Thanks. So loop gain is the product of all gains within the loop? That would work. Strictly it should be A*B*C, where "C" is the 'comparator' (green circle in above figure). For generality, we shouldn't make assumptions about C. In general terms, the model is something like: A_c = (A_o*C)/(1-A_o*B*C), where loop gain is: G_L = A_o*B*C. Is that right? --Trevithj (talk) 00:02, 19 June 2012 (UTC)

The big green thing is not a comparator, just an adder. In typical control loops its drawn with a minus sign, which some then interpret as a comparator. The loop gain is the product of gains around the loop, but sometimes ignores that minus sign when it is there, which is why we has to disambiguate which interpretation we mean. That's probably why there's no source that simply says that positive feedback is defined by loop gain > 0. Also, since each gain is really a complex number dependent on frequency, you can't just count minus signs around the loop as is suggested some sources; in the more general case, you have to do the complex product and look at the sign of the resulting real part to see if the net feedback is positive or negative (and that depends on frequency). Often the positive/negative distinction is take to mean at DC (at zero frequency), in which case it reverts to the simpler real interpretation, in which case you can just see if the number of negative gains is even or odd. Dicklyon (talk) 00:39, 19 June 2012 (UTC)

That is actually what the references say though. The negative/positive feedback thing is a condition in feedback loops. And in a general, non linear, feedback loop, the circuit itself isn't inherently positive or negative, it can depend on amplitude and frequency and time.GliderMaven (talk) 02:15, 19 June 2012 (UTC)

Even in linear systems the way that the complex thing works is that you get a mixture of positive and negative feedback over each cycle, due to the delays through the system, and past 90 degrees phase, the positive feedback tends to win out. There's no radically new thing going on, it's just a derivable consequence caused by the delay.GliderMaven (talk) 02:15, 19 June 2012 (UTC)

Complex numbers makes it easy. Changing between positive negative during every cycle won't lead anywhere useful. Dicklyon (talk) 02:55, 19 June 2012 (UTC)

Of course that is actually how it works though. And not all feedback loops have cyclic inputs.GliderMaven (talk) 03:12, 19 June 2012 (UTC)

Inputs aren't cyclic in general, but inputs for which the concept of "gain" makes sense are the eigenfunctions of the system, which are the complex exponentials, and essentially sinusoids. Dicklyon (talk) 05:14, 19 June 2012 (UTC)

Eigenfunctions imply linearity, but positive feedback loops are commonly highly non linear. Things like hysteresis are usually very non linear. There's nothing wrong with covering linear feedback, but that's not the overall topic, it's certainly an important part of the topic, it's just not the definition.GliderMaven (talk) 12:08, 19 June 2012 (UTC)

If you try and define positive feedback as only occurring in linear systems, then we'd be declaring hysteresis off-topic.GliderMaven (talk) 12:08, 19 June 2012 (UTC)

Because positive feedback diverges, non linearities are much, much more important. With negative feedback, the systems linearise (that's pretty much why negative feedback amplifiers were invented after all), and mathematically linearising the system for analysis works a heck of a lot better in negative feedback, but it doesn't work here very well.GliderMaven (talk) 12:08, 19 June 2012 (UTC)

While you can't use complex exponentials/Fourier analysis to analyze non linear feedback loops in the frequency domain and use that to calculate gain, but that doesn't mean you can't calculate the feedback gain in the time domain, and because you can always do that, and because it turns out that the sign of that gain determines a lot of the behavior, this is why the concept of positive feedback is a surprisingly useful one.GliderMaven (talk) 12:08, 19 June 2012 (UTC)

I don't know a way to measure or define a feedback gain, in the time domain or otherwise, except via a linearization. Am I missing something? Dicklyon (talk) 18:38, 22 June 2012 (UTC)

So you don't know whether ${\dot {x}}=x\left\vert x\right\vert$ is positive feedback?GliderMaven (talk) 19:56, 26 June 2012 (UTC)

I don't even know if it's feedback. But it clearly has an unstable equalibrium at 0, and a linearization at any point could be cast as a linear feedback system with a nonnegative loop gain. Is there some other notion of "gain" there that you can get without a linear approximation at a point? Dicklyon (talk) 21:48, 26 June 2012 (UTC)

"I don't even know if it's feedback." Okkkkk.GliderMaven (talk) 23:02, 26 June 2012 (UTC)

Is every differential equation "feedback"? Dicklyon (talk) 23:06, 26 June 2012 (UTC)

The behaviour of most feedback systems can be described (to an approximation) by differential equations, but then so can weights on springs, tuned circuits, and all kinds of other stuff. That's why it's important not to muddle up mathematical models with actual things. In undergraduate courses, maybe they don't make the distinction clear enough; they're so keen to get ppl familiar with the equations cos that's what the exam will be about. --Nigelj (talk) 23:22, 26 June 2012 (UTC)

If you prefer to phrase it as, "would a system whose behaviour can be mathematically described as... exhibit positive feedback?", that's fine. But I think you'll find that the idea of systems theory is that it doesn't matter what the differential equations are referring to, that if weights on spring or tuned circuits have the same form of equation, then they are dynamically similar systems.GliderMaven (talk) 00:18, 27 June 2012 (UTC)

Still not good enough. Feedback requires that you identify an input and an output, or at least a loop. The differential equation and the dynamics that it describes can come from mechanisms other than feedback. Dicklyon (talk) 04:10, 27 June 2012 (UTC)

Not every differential equation, since trivially ${\dot {x}}=3$ is not an equation that can abstract a feedback loop. Feedback loops have to have a state variable's derivative depend on the variables value, directly or indirectly, and optionally it's history, and they have to be causal.GliderMaven (talk) 00:18, 27 June 2012 (UTC)