Talk:Monte Carlo tree search

Genetic Algorithms?

Better not tell anyone but this looks very like a type of genetic algorithm or evolution driven problem solving, but under a different name. It works by random hunting coupled with testing rules that keep optimal solutions and reject inferior solutions.. The magician puts his hand into the hat and pulls out a rabbit.. :) Lucien86 (talk) 18:28, 25 November 2015 (UTC)

There is a slew of methods that use randomness and testing that are distinct from evolutionary methods. Just because genetic programming uses heuristic it doesn't mean everything that uses heuristics is a genetic algorithm. --Nczempin (talk) 20:51, 8 June 2019 (UTC)

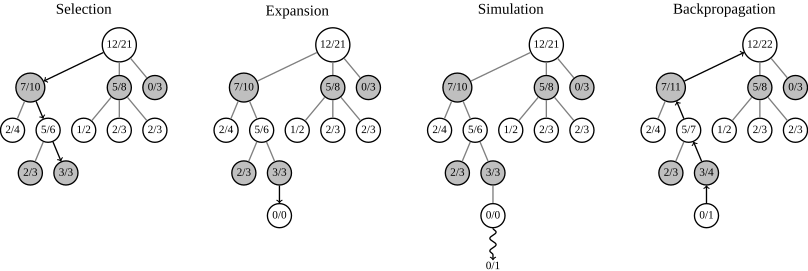
Figure is wrong

The N/D numbers in the image of the four steps of the algorithm are wrong. Whenever a new node is created in an Expansion step, it will end up being characterized as 0/1 or 1/1 depending on whether the simulation leads to a win. In particular, that denominator of 1 for the new node will exceed the sum of the denominators of the node's descendants, because there are no descendants yet, and thus that sum evaluates to zero. Similarly, the numerator will be 0 or 1 more than the sum of numerators of the node's immediate descendants. The back propagation step maintains this status. So at future points in time, each depicted node should have a denominator that is 1 more than the sum of the computed denominators of the node's immediate descendants, and a numerator that is 0 or 1 more that the sum of the numerators of the node's immediate descendants. Right? 𝕃eegrc (talk) 18:29, 1 February 2016 (UTC)

In the first figure, shouldn't the middle node of the second row in each tree be 5/8, not 4/8? — Preceding unsigned comment added by 2620:0:1000:6811:A889:83F6:ED4E:810E (talk) 19:33, 25 May 2016 (UTC)

Figure author here. You're right. This is an SVG file, it's easy to edit and correct it: go ahead! MCiura (talk) 08:45, 6 June 2016 (UTC)

Hi, I corrected and uploaded the image, although I believe I failed with the updating process. I tried and I failed, but the file is there now. See https://commons.wikimedia.org/wiki/File:MCTS_(English).svg --Uncronopio (talk) 15:11, 27 July 2016 (UTC)

Hi! No worries, I updated the figure. For the record: I kept the formatting by editing the file with a text editor. Cheers, MCiura (talk) 16:39, 27 July 2016 (UTC)

Did the new figure make it into the article? The one I am seeing in the article right now does not have the properties

1. A node's denominator must be exactly 1 more than the sum of its immediately descendant nodes' denominators.
2. A node's numerator must be exactly 0 or 1 more than the sum of its immediately descendant nodes' numerators.

𝕃eegrc (talk) 17:00, 27 July 2016 (UTC)

Why +1 and +0/1? Can you please cite a reference that says "must"? Using priors before explaining them would IMHO be confusing. MCiura (talk) 09:00, 28 July 2016 (UTC)

@MCiura, thank you for the question. My "+1 denominator" and "+0 or +1 numerator" rules come from reading the rest of the article. I wouldn't say that they are original research simply because the math is so trivial, at least once one looks at it from the right perspective. In this context, I see it as my job to make that perspective obvious to the other editors. Here goes.

When a node is first created it is either 0/1 or 1/1, meaning that out of one path there is either zero wins or one win, respectively. At this point the node has no labeled immediate children so the sum of the numerators that these children have is an empty sum which is zero. Likewise for the sum of the denominators expressed by the immediate children; it is zero. So, at least at this time point the "+1 denominator" and "+0 or +1 numerator" rules are correct, right?

Henceforth whenever an immediate child of that (now) parent node is created or updated, any increment to the denominator of that child is propagated to the denominator in the parent node; and likewise any increment to the numerator of that child is propagated to the numerator in the parent node. Except for the pictures that show the status between the update of the child and the propagation to the parent, it must be the case that each time the sum across the immediate children changes, so changes the parent.

That is, except with the mid-propagation pictures, the parent node's denominator will always be one more than the sum of the denominators of its immediate children; and the parent node's numerator will always be 0 or 1 more than the sum of the numerators of its immediate children.

If that is still confusing (or wrong), please respond. 𝕃eegrc (talk) 11:59, 28 July 2016 (UTC)

You are perfectly right and I was wrong. It is good that somebody reads the article with understanding once in three years. Feel free to modify the figure! MCiura (talk) 18:46, 28 July 2016 (UTC)

Nitpick: This is true for all nodes except the root node. Its denom is equal to the sum of child denoms plus 0, not plus 1. --mafutrct (talk) 14:24, 8 December 2022 (UTC)

Figure editing isn't really my thing. If you or another editor would take the initiative, I would appreciate it. 𝕃eegrc (talk) 13:49, 29 July 2016 (UTC)

The figure is still wrong. Please, anyone, if you know how to update figures would you make the fixes? 𝕃eegrc (talk) 11:49, 15 September 2016 (UTC)

The figure is still wrong. Please, anyone, if you know how to update figures would you make the fixes? 𝕃eegrc (talk) 12:52, 27 October 2016 (UTC)

@Leegrc: 1) Download the figure, 2) Open it in a text editor, 3) Change the numbers. 4) Upload your version. Cheers, MCiura (talk) 14:50, 27 October 2016 (UTC)

The figure seems overly complex to me, and also looks unrealistic. How could the left branch have reached 2/4 and 1/6? The only possibility I can see is that it was 1/3 1/6 the previous time this branch was explored; 0/2 1/6 before that; and 0/2 1/5 before that? However from that position I think most selection rules would prioritise exploring the 0/2 branch because the uncertainty term dominates the w/n term. I may well have misunderstood, but perhaps this could use some attention from an expert? Servalo (talk) 22:44, 25 December 2017 (UTC)

I've replaced the image. The new one is not SVG sadly. But at least it should have no mistakes, hopefully. --mafutrct (talk) 14:38, 8 December 2022 (UTC)

Broken References

This page contains links to mcts.ai. That domain is not operational. — Preceding unsigned comment added by Swartik (talk • contribs) 15:03, 1 June 2016 (UTC)

Mistake in Expansion-Phase

It says: "Expansion: unless L ends the game with a win/loss for either player, either create one or more child nodes or choose from them node C".

It sounds as though L could already have children. However, in the previous step it has been established that L is a leaf node. It would be more sensible to create all children of L immediately and then choosing one C from them, but of course there may be other formulations. However, the present one does not make sense. — Preceding unsigned comment added by 92.225.225.141 (talk) 11:00, 8 February 2017 (UTC)

Confusing exploration part

• w_i stands for the number of wins after the i-th move;

I understand: During Selection phase for each node considered i is the depth, it is also the move number (like I am at depth 3 so that means this is the second move for the current player and the other player had one move simulated) w_i is the number of leaf nodes (under the current node) that are considered a win.

• n_i stands for the number of simulations after the i-th move;

The cumulated number of simulations under this node.

Is that right ?

Already at this point it does not make sense because the illustration does not correspond to that (leaf nodes are marked with more than one simulation) I confess I am assuming that in the illustration each node is marked with w_i/n_i

Steps of Monte Carlo tree search

Convergence to minimax?

The article states that MCTS converges to minimax, but the link provides no proof for it. I have tried to find the proof or at least the origin of the claim in the literature, but couldn't. In my limited understanding, and after reading a couple papers, the supposed convergence to minimax assumes the results being a Gaussian distribution and not an arbitrary one. This is actually quite a severe restriction and I think it should be pointed out in the article. Games such as chess and go are well known to have positions for which the optimal solution requires deep combinatorial analysis, and for which the "average value" approach will certainly fail. Please let me know if you find the relevant literature or if you think my analysis is flawed. Kilgore T (talk) 11:44, 26 August 2018 (UTC)

I think convergence is guaranteed for any finite game because after an infinite number of simulations the score of every possible move is "estimated" exactly, and matches the minimax value. Of course, this may not mean very much in practice for games like Go that have astronomical numbers of possible games. --Servalo (talk) 16:00, 30 October 2018 (UTC)

Minimax always has a search depth. For any given depth, as long as at each node the probability to choose each move is > 0, eventually you will visit all the nodes at the given depth, regardless of the probability distribution. "Deep combinatorial analysis" is orthogonal to whether MCTS or minimax is used; if you extend one to go beyond the given search depth (for example in Quiescence Search), you can extend the other just as well. It should be fairly easy to see that if MCTS has visited all the nodes (at the given depth, and assuming some kind of way to value these horizon nodes, again orthogonal to MCTS vs. minimax), it will lead to the same move being chosen by MCTS. --Nczempin (talk) 21:04, 8 June 2019 (UTC)

I don't see how these arguments hold water. It is possible, and likely, that there exist in chess positions with poor prognoses or search spaces, however evaluated or sampled, where a single variation spells the difference between winning and losing. Convergence to the average will yield, well, an average, which is poor or losing. But a minimax search is NOT a statistical sampling - if there is a winning line, it will be found. It is believed that is how Lee Sodol beat AlphaGo in the one game of their famous match that he won - because he found that one line in an ocean of otherwise so-so alternatives which AlphaGo converged upon. Sbalfour (talk) 21:18, 12 September 2019 (UTC)

I'm wrong, and here's the citation: "Bandit based Monte-Carlo Planning", Levente Kocsis and Csaba Szepesvari, Machine Learning: European Conference on Machine Learning, 2006 pp. 282-293, http://ggp.stanford.edu/readings/uct.pdf. Sbalfour (talk) 21:32, 12 September 2019 (UTC)

I am sure the basic MCTS (totally random play) in general does not converges to min-max at all, because it underweight singe "expert moves" (the one and only good move in a otherwise bad position). Counterexamples can be found easily by constructing a very small game with such a situation. But the UCT variant does converge as noted in the reference. The proof works bottom up, all possible games are played infinity often, as the number of iterations grows to infinity. At the deepest layer MCTS is perfect by definition, so the layer above is perfect, too. And so on. — Preceding unsigned comment added by 80.255.7.120 (talk) 19:59, 17 September 2019 (UTC)

Wrong algorithm in selection?

"Selection: start from root R and select successive child nodes until a leaf node L is reached"

"a leaf is any node from which no simulation (playout) has yet been initiated."

"Expansion: ... create one (or more) child nodes and choose node C from one of them"

This is incorrect. Consider root with one child A which is selected randomly at expansion. The next selection will not be able to consider the parallel child B, because B is not a leaf, and by the recursive selection, A will be selected and expanded again because it is the only leaf, infinitely so. The MCTS search trivially reduces to the expansion strategy in this case.

The space of selection from each parent node is all the states reachable from that state. This includes nodes that are not yet in the explored graph as leaves. Or else, at expansion step, all children of the node must be added to explored tree.

Please take a look at page 6 of http://mcts.ai/pubs/mcts-survey-master.pdf . "A node is expandable if it represents a nonterminal state and has unvisited (i.e. unexpanded) children". An expandable node is not necessarily a leaf. Note that the paper's formulation of MCTS is not consistent with the selection expression in section Exploration and exploitation, because the criterion to stop at a non-leaf node is not given. For sake of consistency, again, the space of selection should be all children states accessible from that state. The best children states should be expanded immediately without other criterion. Simulation start from these nodes.

Please correct me if I'm wrong. Thank you. Huya01 (talk) 09:26, 7 November 2018 (UTC)

Clumsy phrase

> the {\displaystyle \beta (n_{i},{\tilde {n}}_{i})} {\displaystyle \beta(n_i, \tilde{n}_i)} function should be close to one and to zero for relatively small and relatively big ni and {\displaystyle {\tilde {n}}_{i}} {\displaystyle \tilde{n}_i}, respectively.

Ehm...2001:700:1200:5120:98F5:8877:83BD:703C (talk) 10:15, 4 January 2019 (UTC)

Is the current figure correct?

As you can see here that figure has a discussion in 2016, but in 19 November 2017, user Dicksonlaw583 changed the figure heavely https://en.wikipedia.org/w/index.php?title=Monte_Carlo_tree_search&diff=811051956&oldid=809186144

From a figure that adds rewards up to the first layers and you can use UCT in every layer that will lead you to the selected leaf. One possible mistake of the image is that one mid layer (7/10) is the sum of their childs (2+5 = 7, 4+6 = 10), that may be ignoring that at the begining this was a leaf node 0/1 or 1/1 and when you have two childrens with 4 and 6 visits this will be 4+6+1 = 11, an wins can be 7+0 or 7+1. Other problems can be that all leaf have /3 visits but we can supose that they run 3 simulations and we can ignore this.

Steps of Monte Carlo tree search

To a figure that only adds rewards in layers that represents the player who wins. This is why in step 3 the output is "white loose" and backprop increments evaluation counters (n) in all layers but only increment win counters of black nodes (3/3 -> 4/4 and 7/10 -> 8/11)

Steps of Monte Carlo tree search

The problem with that is if you are on the root you see UCT values for all 3 childs: Current 11/21, UCT for node 7/10 = 1.480 <-- Max Current 11/21, UCT for node 0/3 = 1.425 Current 11/21, UCT for node 3/8 = 1.247

And select 7/10, like in the example, but then you perform again UCT: Current 7/10, UCT for node 2/4 = 1.573 Current 7/10, UCT for node 1/6 = 1.043

And now the maximum UCT value is for 2/4, while the example selects 1/6. With 5/6 (the previous image) 5/6 will be the node with higher UCT: Current 7/10, UCT for node 5/6 = 1.709

But now the example image doesn't follow the algorithm.

I think that the previous image was right, and not the actual. Is the same that you can see in this class video https://www.youtube.com/watch?v=UXW2yZndl7U (he spread the simulation/rollout to every layer) and you can use UCT in every layer (as described in wikipedia article in: Monte_Carlo_tree_search#Exploration_and_exploitation). Another video that shows this is: https://www.youtube.com/watch?v=Fbs4lnGLS8M

Update/Small answer: I tried to implement it in a connect 4 game and yes, you need to update nodes based on the represented player on the nodes. I supose that update all nodes up to the root only works on scenarios without adversarials. But this doesn't change that the image have some errors — Preceding unsigned comment added by Dagavi (talk • contribs) 07:14, 27 August 2020 (UTC)

Yep. The image is completely wrong, I'm afraid. The numbers make no sense. Also see the previous discussion above. --mafutrct (talk) 14:20, 8 December 2022 (UTC)