Talk:Matrix multiplication/Archive 1

Archive 1

Matrix Concatenation Links Here. Why?

Why does matrix concatenation redirect to this page? I did not find a single use of the words concatenat* in this document.Klappck (talk) 18:50, 14 April 2011 (UTC)

Dot products of vectors

A good way to envisage matrix mult is to split the first into rows, the 2nd into columns, and vector dot-produc them. --anon

Matrix multiplication can also be envisages a dot products of vectors. The above example becomes::

${\begin{bmatrix}\mathbf {a} _{1}\\\mathbf {a} _{2}\end{bmatrix}}*{\begin{bmatrix}\mathbf {b} _{1}&\mathbf {b} _{2}\end{bmatrix}}={\begin{bmatrix}\mathbf {a} _{1}\cdot \mathbf {b} _{1}&\mathbf {a} _{1}\cdot \mathbf {b} _{2}\\\mathbf {a} _{2}\cdot \mathbf {b} _{1}&\mathbf {a} _{2}\cdot \mathbf {b} _{2}\end{bmatrix}}$

The above is for the article, but trying to get the numbers right makes my brain ache. I'm leaving it here in case I've got them wrong. -- Tarquin 17:30 Jan 15, 2003 (UTC)

Perhaps it is good to work with column vectors; then the a's on the left must get a T for transposed. - Patrick 17:39 Jan 15, 2003 (UTC)

yup, that's the right way to do it.

I like that way a lot better than the other way, and I think the above general formula should be on the page. How I usually envision it is I write a horizontal line, then a verticle line, representing a lines of vectors. Its simpler to me to write a matrix of dotted vectors, rather than handle every element of the matrix separately. Fresheneesz 08:35, 21 March 2006 (UTC)

After reading over the "proportions-vectors method" I don't have any idea what it means by proportions.. Perhaps that should be explained better? Fresheneesz 08:37, 21 March 2006 (UTC)

"we take once the first vector and twice the third vector, while ignoring the second vector"

I'm pretty sure we're not gonna "ignore" anything, you multiplied the second vector by 0. I'm going to change that so it doesn't sound as .. vapid.. (no offense). Unless anyone argues. Fresheneesz 08:39, 21 March 2006 (UTC)

Picture

Okay, here's something that is probably one of these things that only makes sense to me.

When this picture was posted, it looked different. Find the original here.

it basically shows that the entries of the product matrix are filled in according to which row and column are multiplied. If anyone else gets it & thinks it useful for the article , please add it -- Tarquin 23:46 Jan 21, 2003 (UTC)

(except I've just realised the result matrix in the pic has the wrong number of rows .... hmmmmm. if there's a call for it I'll remake it)

Surely it makes sense to me also! This diagram uses unequal m and p, which is better (more general). I would use the diagram and add a third column for B in the example. - Patrick 01:14 Jan 22, 2003 (UTC)

Ah, that's good to know! There are many concepts in maths that I envisage pictorially in some way... and then I find that nobody else does... very disconcerting! Well, if one more person gets it, we'll put it in the article :-) -- Tarquin 23:03 Mar 14, 2003 (UTC)

This is the best illustration of matrix multiplication I've ever seen. In fact, I think it's one of the best math illustrations on Wikipedia. The second I saw it, I 'got' matrix multiplication for the first time. Beautiful work. Fredrik | talk 23:24, 10 Mar 2005 (UTC)

I fixed the picture, making it have correct number of rows. I also added yellow highlight around the elements that are being used, cause before it could have looked like only two elements were going into the new cell (the cells from which the arrow starts). Thats how I saw the picture so it confused me. I think the outline helps clarify that confusion. Fresheneesz 09:47, 21 March 2006 (UTC)

It looks like you've messed up the description. In the matrix operation AB, the column count from A and the row count from B are taken to form the resulting matrix AB. In other words, the operation shown in your picture is BA, not AB. —The preceding unsigned comment was added by CodeMercenary (talk • contribs) 07:35, 9 April 2007 (UTC).

I created a modified version of the image on the page. I added the names for the items in the matrix (a_1,2 etc) to make it clearer how the multiplication works. Do you agree that this image is better? Would like comments before inserting it. Lakeworks (talk) 23:03, 14 January 2008 (UTC)

Two minor suggestions (which are a matter of taste):

1. Make the cells square, and mark the two targets with non-flattened circles.
2. Also fill in the "unused" cells of A and B: a_2,1 etcetera, using a grey colour.

 --Lambiam 06:45, 15 January 2008 (UTC)

Updated the image with the suggestions you made. Any more suggestions or can I update the image in the article?

Lakeworks (talk) 21:11, 16 January 2008 (UTC)

It's fine with me (but I can't speak for other editors).  --Lambiam 01:47, 17 January 2008 (UTC)

Go for it. -- Jitse Niesen (talk) 15:12, 17 January 2008 (UTC)

This image is very helpful for me to refresh my memory, thanks for the addition Lakeworks. James Lednik (talk) 00:21, 14 February 2008 (UTC)

This image does not match the example. The example results in a 2x2 matrix and the example results in a 3x3. Would it be easier to understand if they matched? —Preceding unsigned comment added by 128.112.151.175 (talk) 02:01, 7 April 2009 (UTC)

Directly next to the picture it says: "For example BA:" and lists the BA multiplication. That is confusing, as the picture shows the AB multiplication. I agree that BA should also be shown, but first show the AB numbers that go with the picture! --96.234.240.247 (talk) 13:11, 24 April 2009 (UTC)

Lakeworks's version of the image better illustrated the concept, in my opinion. It showed unequal dimensions, i.e. with A mxn and B nxp, C is mxp. Could we restore it? --StefanVanDerWalt (talk) 14:07, 4 October 2010 (UTC)

HTML representation

While I love HTML, the statement:

(the HTML entity ⊗ (⊗) represents the direct product, but is not supported on older browsers)

seems out of place. This article is about matrix multiplication, not HTML. Thoughts?

I've seen another article which had a simliar comment, and the consensus was to leave it because "people deserve to know how to write it" or something. I think its small, and should be at the end, but be there none the less. Fresheneesz 08:35, 21 March 2006 (UTC)

Thank you! I cannot imagine things pictorally well, and I always forget the algorithm for Matrix Multiplication. This picture is a lifesaver! wiki@matthewwilkes.name

Error in Kronecker Product Section

In the Kronecker product section, I believe there is an error.

${\begin{bmatrix}a_{11}B&a_{12}B&\cdots &a_{1n}B\\\vdots &\vdots &\ddots &\vdots \\a_{n1}B&a_{n2}B&\cdots &a_{mn}B\end{bmatrix}}$

Should be:

${\begin{bmatrix}a_{11}B&a_{12}B&\cdots &a_{1n}B\\\vdots &\vdots &\ddots &\vdots \\a_{m1}B&a_{m2}B&\cdots &a_{mn}B\end{bmatrix}}$

Right??

Yup. There should be an m. Fixed it. -- Tarquin 18:14, 22 Jun 2005 (UTC)

partitioned matrices

There needs to be some explanation of Partitioned matrix algrbra especially with respect to multiplication. I don' the math software so I hereby throw the ball to someone else. MPS 14:53, 20 Jun 2005 (UTC)

Notation

It is quite unusual to write AxB for the matrix product. AB or if necessary A.B is commonly used. Also, for multiplying numbers one uses 3x4 and not 3.4. The dot is used for the product of variables: a.b if just writing ab would lead to confusion.Nijdam 23:14, 28 February 2006 (UTC)

I agree that A × B for the matrix product is very uncommon, and I edited the article accordingly. However, I've encountered the notation 2 · 3 for the product of the numbers 2 and 3 quite often, so I left that one in. -- Jitse Niesen (talk) 11:20, 2 March 2006 (UTC)

Yeah, straight juxstaposition is probably the most common thing.... but I have another observation. I think that the subscripting is quite clear in general, but separating indices with a comma conflicts with the use of commas before an index in general (virtually ubiquitous) tensor notation as a means of indicating differentiation with respect to the index following the comma. I think the article is so clear and useful that this should not be taken as a severe criticism and I am not motivated to "boldly" change this. Perhaps a brief discussion about whether this should be attended to is a better idea. scanyon 01:42, 20 February 2010 (UTC) —Preceding unsigned comment added by Patamia (talk • contribs)

howto's belong in wikibooks

wikipedia should just say what matrix multiplication is

I agree. This is a how to, and doesn't belong in an encyclopedia any more than the receipe for goat stew.

I disagree. This is exactly the information I was looking for when I searched for Matrix Multiplication. This article does not represent a how to, only an appropriately rigorous explanation of what matrix multiplication is.

I also think that this article is both fine in general and extremely useful even in an encyclopedia context. How an "operation" is defined often entails explaining "how" the operation is performed. Beyond that there is a "matter of taste" issue, but in this particular case, I vote to certify this article as more than worthy to remain in the encyclopedia. I have a reasonably broad and in several respects advanced background, but when I want to remind myself of what something IS I become exceedingly dismayed when I encounter a Wikipedia article that is so esoteric and so dependent on foreknowledge of advanced notation that is is effectively useless. I understand that there is a justifiable concern about whether an encyclopedia article should be pedagogical, but for some fairly fundamental mathematical definitions I think that explaining what something is becomes indistinguishable from explaining how it works.scanyon 01:36, 20 February 2010 (UTC) —Preceding unsigned comment added by Patamia (talk • contribs)

I too agree that this is an excellent and relevant article and should be kept as-is. 10:42, 24 January 2011 (UTC) — Preceding unsigned comment added by 51kwad (talk • contribs)

The coefficients-vectors method

In the example, it jumps from [3 1]+[0 0]+[2 0] to [5 1] without any explanation. I've had every edit I've made to a math page reverted, so I will suggest here that an extra step be added to point out how you get from the first step to the next. It is [(3+0+2) (1+0+0)]. Without that, it is not obvious what is going on unless you already know matrix multiplication - and if you did, you wouldn't be reading this article. --Kainaw ^(talk) 14:57, 2 September 2006 (UTC)

I think it's pretty obvious as it is. The [a b] is notation for a vector, so k[a b] = [ka kb] and [a b] + [c d] = [a+c b+d] (by linearity). Adding in the additional step does clutter things up a bit. —Preceding unsigned comment added by 129.31.68.254 (talk) 00:05, 1 September 2008 (UTC)

proportions matrix?

In "properties, what the proportions matrix means?

The article either needs to explain or avoid this usage. The "proportions" matrix is the left-hand matrix and the "vector" matrix is the right-hand matrix. Paul D. Anderson 23:13, 6 October 2006 (UTC)

Inner product

Is there a word for taking the inner product of two matrices as though they are vectors? That is

$x=\sum _{i,j}M_{ij}M_{ij}=M:M=M_{11}+M_{12}+\cdots +M_{21}+M_{22}+\cdots$

So, is there a name for this? —Ben FrantzDale 17:03, 20 December 2006 (UTC)

I'm not completely sure what you mean, but I think you're talking about the "Frobenius inner product". For two m-by-n matrices A and B, that is defined by

$\langle A,B\rangle _{F}=\operatorname {trace} (AB^{\top })=\sum _{i=1}^{m}\sum _{j=1}^{n}a_{ij}b_{ij}.$

You need to take conjagates for complex matrices. This inner product leads to the Frobenius norm, but that seems to be the only reference on Wikipedia to the Frobenius inner product. -- Jitse Niesen (talk) 18:16, 20 December 2006 (UTC)

That's the one. Thanks. Do you think it would be appropriate to define Frobenius inner product on this page? —Ben FrantzDale 21:14, 20 December 2006 (UTC)

Yes, it could be mentioned. Perhaps another page would be more appropriate, but I'm not sure which one, so just add it here. -- Jitse Niesen (talk) 16:47, 21 December 2006 (UTC)

Will do. It looks like this is closely related to Frobenius algebra. I don't know enough of the details to be able to say how these topics should be divvied up among pages, though. —Ben FrantzDale 18:03, 21 December 2006 (UTC)

This article sucks

I nominate that this article gets the suck award. 136.159.197.83 20:44, 17 April 2007 (UTC)

Totally disagree. This is an excellent article, and should stay. 51kwad (talk) 10:44, 24 January 2011 (UTC)

I totally agree w/ the first commenter. This article jumps immediately into the overly-technical lingo. A better way to organize it would be to include a less advanced explanation first - something at the level of high-school algebra (where students are first introduced to matrices). This should include a couple of examples, and the worked solutions. The first example using two 2x2 matrices is helpful, but then there's no corresponding example for multiplying two matrices of different dimensions. If you can only use one example, it would be better to move the "Illustration" section to the top of the article (product of a 4x2 matrix and a 2x3 matrix). The cement/chalk/plaster problem is a nice example, but it doesn't include the worked solution, only the final answer. So it should go after the Illustration.

So far, the most plain-English explanation, which would be most accessible to beginners, is the second paragraph entitled "Alternative Explanation". As for the first paragraph called "Non-technical details"... are you kidding me? How much more obscure can you get? Just because one writes something with only words (i.e no numbers/symbols), doesn't mean they have any clue about being "non-technical".

The more advanced technical discussions are fine to include, but it should come after the basic stuff. If you want this to be informative and accessible, you need to recognize that some of the readers are just starting out with matrices. If you want it to be Inaccessible to them, and continue to reinforce their Dislike of math, then by all means keep the article exactly the way it is!

ElizabethRogers (talk) 00:55, 23 October 2011 (UTC)

I'm lost

What is r, is this rows? Please define the variables in the example before using them. I'm looking somewhere else for something easier to follow. —Preceding unsigned comment added by 72.230.164.82 (talk) 18:32, 11 October 2008 (UTC)

Article needs a good simple illustration

Maybe something like the Generalized Example here http://www.mathwarehouse.com/algebra/matrix/multiply-matrix.php —Preceding unsigned comment added by 213.104.208.37 (talk) 15:50, 3 December 2010 (UTC)

way too complicated

seriously how is the average joe meant to understand this? please could someone simplify it

I agree, I just wanted to see how to simply multiply 2 matrices; and multipy a scalar and a matrix, but this is site didn't help. —Preceding unsigned comment added by 129.21.40.143 (talk) 22:15, 11 February 2008 (UTC)

You are right. This page could do with a simple introduction. In my junior-high curriculum, we ran into matrix multiplication in 8th grade (age 12ish), well before I ever saw summation notation and well before we saw any applications for matrices. I just added a little bit, but more could be added to make this article much more accessible. While it's easy to state the algorithm for matrix–matrix multiplication, I find it impossible to understand before you have an intuition for what the vectors themselves mean. Then matrix–vector multiplication is just a way to make a new vector by having each entry in the new vector be some weighted sum in the initial vector. Then matrix–matrix multiplication is the "right" way to find P=BA such that Px=BAx. I hope that helps and I hope people work to make this article more approachable. —Ben FrantzDale (talk) 01:33, 12 February 2008 (UTC)

What the article needs is some examples for multiplying simple matrices (e.g. 2x2 and 3x3). People who aren't familiar with the other notation will most likely only need that. Andrewy (talk) 02:08, 8 December 2008 (UTC)

Why would the average joe want to read this article? And why should an encyclodedia be designed for the average joe? The proper context for introducing the matrix product is Linear Transformations of Vector Spaces and Modules, but that would be beyond most readers. However, it is good to have technical articles in WP. 51kwad (talk) 10:52, 24 January 2011 (UTC)

Elitist much? Wow, talk about self-important. Granted, the term "average joe" might be a bit of a stretch, but how about the "average beginner", i.e. someone who is just learning matrices? And lets face it, this isn't really an Encylopedia anyway. It's a tertiary reference at best. No academic mathematician would ever be caught dead citing Wikipedia, period. If you don't realize that, than clearly you don't deserve to be as self-important as you think you do. Most users of Wikipedia are (or should be) looking here mainly as a starting point. It's completely reasonable for others to want the article to be more accessible to a larger audience of readers.

In summary, get over yourself. ElizabethRogers (talk) 01:11, 23 October 2011 (UTC)

Broken link?

The link for "Efficient Matrix Multiplication for single dimension arrays" (http://angelo.freeshell.org/computer/docs/mmult.php) appears to be down (503 error). Is there another reference to that article? A google search didn't find it. -- Ed Burnette

An copy archived on 10 May 2007 is available at http://web.archive.org/web/20070510025901/http://angelo.freeshell.org/computer/docs/mmult.php . However, I don't think it is a useful resource, so I removed the link. -- Jitse Niesen (talk) 04:39, 2 August 2007 (UTC)

Possibility of adding a section explaining why matrices work the way they do

Does anyone else think that it wouldn't harm to mention how matrices can be seen as maps between vector spaces and that matrix multiplication corresponds to the composition of maps (after picking a basis)? LkNsngth (talk) 03:50, 3 May 2008 (UTC)

It is important to add that. Matrix multiplication is defined in such a seemingly non natural way because it corresponds precisely to composition of associated linear transformations. A new section might be in order.--Shahab (talk) 04:48, 3 May 2008 (UTC)

I've started working on such a section.  --Lambiam 16:34, 3 May 2008 (UTC)

 Done; please review and improve.  --Lambiam 18:07, 3 May 2008 (UTC)

I believe there was a small technical error in your writing, a vector space is constructed over a field. Modules are generalizations of vector spaces over a ring. Other than that it looks good LkNsngth (talk) 23:18, 5 May 2008 (UTC)

That means that matrices over integers are excluded, so I removed the reference to integers. -- Jitse Niesen (talk) 08:38, 6 May 2008 (UTC)

Powers of matrices

Powers of square matrices are a special case of matrix multiplication, so it seems to me they should be at least briefly discussed in this article. I'm going to add a brief section on this topic; please remove if there's a problem and I'll help improve it or find some other place to put it, but I really think there needs to be some coverage of this topic on Wikipedia. Swift1337 (talk) 05:47, 16 October 2008 (UTC)

OK, I've added it. It's pretty barebones and could use some discussion of convergence of powers of matrices, but I think it'll be useful as a starting point at least. Swift1337 (talk) 06:07, 16 October 2008 (UTC)

Change example matrix

The example matrix is a bad one because the outer dimensions are the same too. This might give the false impression that the matrices have to have rotated dimensions. I would recommend adding a row to the first one, making it the same size as the picture. Asmeurer (talk ♬ contribs) 17:21, 15 November 2008 (UTC)

I agree that this example would be improved if the matrices had different outer dims. BeckyAn (talk) 01:04, 7 December 2008 (UTC)

Should coalesce two properties sections

There are two "properties" sections -- Properties in the upper-third of the page, and "Common Properties" tucked down amongst the different specialized products. I propose consolidating them, into the earlier of the two sections. BeckyAn (talk) 01:04, 7 December 2008 (UTC)

premultiplication and postmultiplication

If I make the product AX, I premultiply X by A. If I make the product XA, I postmultiply X by A.

Is this the right usage of premultiplication and postmultiplication? Are these words authorized terms or slangs?

I'm a stranger in English. Bmack7264 (talk) 09:10, 3 June 2009 (UTC)

I'm no native either, but I think it is more common to say left and right multiplication. Jakob.scholbach (talk) 11:09, 3 June 2009 (UTC)

Clean-up

This article is a hodge-podge of different topics, and I feel that it would be worthwhile to restrict the scope to just the standard matrix product. Majority of the other topics have their own dedicated "main" articles.

I've begun the clean-up by correcting some errors, streamlining and rearranging the material in the most important section on the matrix product. I removed a lengthy and non-informative subsection illustrating the composition, which also violated WP:NOTTEXTBOOK. Several other sections run afoul of the same policy, in my opinion. Weighted matrix product is potential OR and is next in line for deletion, unless a serious case is made for preserving it, possibly as a separate article. Also, I am less than enamoured by non-standard notation in the subsection illustrating the matrix multiplication, which sports sexy different colors, but mixes latin characters and arabic numerals in referencing matrix entries. Certainly, much work remains to be done. Arcfrk (talk) 06:04, 2 September 2010 (UTC)

Thanks for calling attention to this. The article should, of course describe how matrices are multiplied, but giving several explanations with multiple examples crosses into HOWTO/TEXTBOOK territory. I'm thinking that some of this material should be merged in Wikibooks instead of deleted; with a link from this article people who are looking for a textbook style treatment will be able to find it easily. I did find a couple of brief mentions in a Google search on weighted multiplication, so I don't think it's entirely OR, but I doubt there is enough material out there for it to be encyclopedic and I'm sure major parts of the section are OR. So I'd agree that the section should be deleted unless significant improvements are made and references added. I agree also that the sections which describe other types of multiplication have content fork issues and should be removed or at least shortened to a single sentence. This would be in keeping with summary style, but besides that I think these other types of multiplication are separate subjects and don't really belong here. I'm all for collecting similar subjects together to make a half-decent article from a collection of stubs, but to me matrix multiplication is really a way to compute the composition of linear maps and these other forms of multiplication have little to do with that. I'd also note that the lead section does not seem to be in line with the MOS and could probably use a rewrite.--RDBury (talk) 08:24, 2 September 2010 (UTC)

The "The Weighted Matrix Product" section keeps being re-inserted by the same user, User:Cloudmichael. As far as I can tell, the section is pure WP:OR. A comment[1] left by User:Cloudmichael at User talk:Sławomir Biały (after Sławomir Biały removed that section), indicates that User:Cloudmichael does not understand that Wikipedia does not publish original research. Nsk92 (talk) 11:50, 5 September 2010 (UTC)

Product

I'm not sure whether every matrix necessarily has to be considered as the representation of a linear map. That's why I didn't refer to this in the introduction. Nijdam (talk) 09:54, 5 September 2010 (UTC)

Recent changes

I just removed the following:

( This is wrong. for symetric matrices the following holds: AB = (BA)^T , please revise this Zvi N )

The article should not be used for comments about the article. And the above comment is incorrect, the article as written is not wrong. The article says

... if A and B are both diagonal square matrices, or more generally they are equal to their transpose A^T=A and B^T=B, and of the same order then AB = BA.

This implies AB = (BA)^T. A = A^T is the same as saying A is symmetric. And if A and B are symmetric then so is their product. So (BA)^T = BA, and AB = (BA)^T follows from AB = BA. The article as written is correct, and does not need changing as it describes the conditions under which matrices commute. The above information adds nothing useful.--JohnBlackburne^words_deeds 09:36, 17 April 2011 (UTC)

Great job clarifying that. Millertime246 (talk) 01:02, 23 October 2011 (UTC)

Article order etc.

I just undid a change which mostly involved reordering the content. Diving straight into the example makes it much harder to follow as there's no sense of the process being followed or why the matrices can be multiplied. It would be better to expand the lead which is far too short for this article, and let that serve as a more general introduction. Apart from that the biggest issue seems to be pages of examples presented in various styles which could probably be simplified. This is an encyclopaedia not a textbook and examples should be kept to a minimum, making it easier to follow and find the factual content.--JohnBlackburne^words_deeds 02:25, 23 October 2011 (UTC)

Extra diagram

What do people think of this diagram for illustrating how matrix elements are multiplied across rows/columns?

I know there is an illustration already, but mine shows the "mental path" that could be traced when following the matrix elements in performing the calculation.

Correspondance between row and column elements in matrix multiplication. The first element in the row is multiplied with the first element in the column, the second in the row with the second in the column etc. - then all these products are added up.

Correspondance between row and column elements in matrix multiplication. The first element in the row is multiplied with the first element in the column, the second in the row with the second in the column etc. - then all these products are added up.

--Maschen (talk) 23:05, 3 December 2011 (UTC)

Doesn't work for me: I know how to multiply matrices so recognise the bit on the left but the bit on the right is far less obvious. They look like very different things, not two ways of drawing the same thing. And that's even with reading the caption: but that's far too long for an image caption, by about four of the five lines, so it won't be read by most readers. It's also very large for an image, which doesn't disqualify it but is only justified I think if a smaller inline image isn't possible. But it is possible as there's already an image there, one which contains more information and so is clearer.--JohnBlackburne^words_deeds 23:25, 3 December 2011 (UTC)

Splendid. Already a failure and waste of time. Thanks for feedback. What do others think? If no one replies forget it happened and i'll delete. If others dislike (most likley) then its also a delete.--Maschen (talk) 00:07, 4 December 2011 (UTC)

I decided to split the image in two so people can decide which is better (next to zero chance of success but I'll do it anyway). I shouldn't say the caption was a problem - thats the easy part to fix, and it has been contracted.--Maschen (talk) 08:52, 4 December 2011 (UTC)

Make better

Here is what I propose to improve the article:

Major issues

• Perhaps one reason for the "techincally difficult" tag is the "Application example". Its very confusing. Why explain the general principle then run into a confusing real life example? Can it seriously be considered easy to follow by a typiacal reader? It doesn't matter if "a company sells whatever whatever" and "Acen/Build/etc. bought whocares whatnot" Why not just use a purley mathematical example/s? Here's what I would add:

Click to see examples - long list

Just use one or two - not all.

"Given the matricies: $\mathbf {A} ={\begin{pmatrix}1&2\\10&5\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}3\\8\\\end{pmatrix}}$

their matrix product is:

$\mathbf {AB} ={\begin{pmatrix}1&2\\10&5\\\end{pmatrix}}{\begin{pmatrix}3\\8\\\end{pmatrix}}={\begin{pmatrix}1\times 3+2\times 8\\10\times 3+5\times 8\\\end{pmatrix}}={\begin{pmatrix}19\\75\\\end{pmatrix}}$

but BA is not defined.

If $\mathbf {A} ={\begin{pmatrix}1&0\\9&3\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}2&9\\6&5\\\end{pmatrix}}$

their matrix products are:

$\mathbf {AB} ={\begin{pmatrix}1&0\\9&3\\\end{pmatrix}}{\begin{pmatrix}2&9\\6&5\\\end{pmatrix}}={\begin{pmatrix}1\times 2+0\times 9&1\times 9+0\times 5\\9\times 2+3\times 6&9\times 9+3\times 5\\\end{pmatrix}}={\begin{pmatrix}2&9\\36&116\\\end{pmatrix}}$

and

$\mathbf {BA} ={\begin{pmatrix}2&9\\6&5\\\end{pmatrix}}{\begin{pmatrix}1&0\\9&3\\\end{pmatrix}}={\begin{pmatrix}2\times 1+9\times 9&2\times 0+9\times 3\\6\times 1+5\times 9&6\times 0+5\times 3\\\end{pmatrix}}={\begin{pmatrix}83&27\\51&15\\\end{pmatrix}}$

If $\mathbf {A} ={\begin{pmatrix}1&{\sqrt {3}}&0&9\\4&2&3&0\\-{\sqrt {2}}&1&1&1\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}a&c\\3&8\\2&1\\0&b\\\end{pmatrix}}$

their products are:

${\begin{aligned}\mathbf {AB} &={\begin{pmatrix}1\times a+{\sqrt {3}}\times 3+0\times 2+9\times 0&1\times c+{\sqrt {3}}\times 8+0\times 1+9\times b\\4\times a+2\times 3+3\times 2+0\times 0&4\times c+2\times 8+3\times 1+0\times b\\-{\sqrt {2}}\times a+1\times 3+1\times 2+1\times 0&-{\sqrt {2}}\times c+1\times 8+1\times 1+1\times b\\\end{pmatrix}}\\&={\begin{pmatrix}a+3{\sqrt {3}}&c+8{\sqrt {3}}+9b\\4a+6+6&4c+16+3\\-a{\sqrt {2}}+3+2&-c{\sqrt {2}}+8+1+b\\\end{pmatrix}}\\&={\begin{pmatrix}a+3{\sqrt {3}}&9b+c+8{\sqrt {3}}\\4a+12&4c+19\\-a{\sqrt {2}}+5&-c{\sqrt {2}}+b+9\\\end{pmatrix}}\end{aligned}}$

but again BA is not defined.

If $\mathbf {A} ={\begin{pmatrix}\cos \phi &\sin \phi &0\\-\sin \phi &\cos \phi &0\\0&0&1\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}x&p\\y&q\\z&r\\\end{pmatrix}}$

their matrix products are:

${\begin{aligned}\mathbf {AB} &={\begin{pmatrix}(\cos \phi )x+(\sin \phi )y+0\times z&(\cos \phi )p+(\sin \phi )q\times r\\(-\sin \phi )x+(\cos \phi )y+0\times z&(-\sin \phi )p+(\cos \phi )q\times r\\0\times x+0\times y+1\times z&0\times p+0\times q+1\times r\end{pmatrix}}\\&={\begin{pmatrix}x\cos \phi +y\sin \phi &p\cos \phi +q\sin \phi \\-x\sin \phi +y\cos \phi &-p\sin \phi +q\cos \phi \\z&r\end{pmatrix}}\end{aligned}}$

once again BA is not defined. This illustrates in general that matrix multiplcation is not commutative."

I.e. use examples the reader can follow progressivley. The current example is silly.

• The Illustration section (not the actual image) could be better, in terms of how the maths is laid out. This is what I would have done:

"If A is an n × m matrix, and B is a m × p matrix, that is,

$\mathbf {A} ={\begin{pmatrix}\cdot &\cdot &\cdot &\cdots &\cdot \\a&b&c&\cdots &x\\\cdot &\cdot &\cdot &\cdots &\cdot \\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}\cdot &\alpha &\cdot \\\cdot &\beta &\cdot \\\cdot &\gamma &\cdot \\\vdots &\vdots &\vdots \\\cdot &\xi &\cdot \\\end{pmatrix}}$

the procedure for multiplying elements in the rows of matrix A to the corresponding elements in the columns of B is as follows. Elements in row i of A multiply by elements in column j of B, the final answer is in row i column j of the resulting matrix AB:

${\begin{pmatrix}\cdot &\cdot &\cdot &\cdots &\cdot \\a&b&c&\cdots &x\\\cdot &\cdot &\cdot &\cdots &\cdot \\\end{pmatrix}}{\begin{pmatrix}\cdot &\alpha &\cdot \\\cdot &\beta &\cdot \\\cdot &\gamma &\cdot \\\vdots &\vdots &\vdots \\\cdot &\xi &\cdot \\\end{pmatrix}}={\begin{pmatrix}\cdot &\cdot &\cdots &\cdot \\\cdot &(a\alpha +b\beta +c\gamma +\cdots x\xi )&\cdots &\cdot \\\cdot &\cdot &\cdots &\cdot \\\vdots &\vdots &\ddots &\vdots \\\cdot &\cdot &\cdots &\cdot \\\end{pmatrix}}$

..."

(or words to that effect) instead of all those colourful formulae dotted around before and after the matrix illustration, an odd mix of symbols containing row/column indicies and letters and numbers. It would also be better not having numbers, and only using letters systematically, that way is completely general and more comprehensible. Numbers are better left for examples. Also, matricies of specfic sizes are used. This above is more general.

• The current image is fine, but how about adding the left of the above images proposed by Maschen (not the right)? I think the left seems ok, the right may be confusing. Could be added somewhare in the Technical details section, since it contains indexed elements.
• In the Properties of matrix multiplication section, why is scalar multipication mentioned before fully explaining it? shouldn't that section Scalar multiplication be at least before the properties? (Before/after matrix multiplcation itself doesn't matter). It makes the article disjointed.
• Shouldn't Powers of matrices section be after the properties of matrix multiplication? All the other products should come after this since the power of a matrix refers to matrix multiplcation and is not relavant for the other forms of matrix product. This is also a slight discontinuity.

Minor issues

• In the first 1/2 of the article, the matrcies are writen in italic, then later in bold. All letters for matrcies should be bold (not components, the full matrix).
• I seriously don't think colours should ever be used in maths formulae, in case the reader is colour blind. By that argument you could defeat every coloured diagram though... but here the examples rely on colour coordination. However I never plan to change this feature on any wikipedia article - its up to whoever likes/wants it.

To be honest it was so tempting to simply do this to the article. But then it would immediatley be reverted. Anyway its better to show others first.

-- F = q(E + v × B) 20:03, 16 December 2011 (UTC)

Actually never mind about my proposed change to the Illustration section - didn't even realize that it directly refers to the diagram...

-- F = q(E + v × B) 20:13, 16 December 2011 (UTC)

Too technical?

This is as easy as it gets! Very good article IMHO. I propose the banner be removed? 51kwad (talk) 10:39, 24 January 2011 (UTC)

I believe I put the banner up. The article is currently rated C class which is two grades removed from good. The second sentence of the lead doesn't help anyone who is not already familiar with the advanced concepts linked there. There are two intimidating equations in the first section. The goal is to make it understandable to non-experts (e.g. someone trying to get help with their math homework). The Illustration section would be better place to start than "composition of the linear transforms". Let me know if further (hopefully) constructive criticism is needed. --Kvng (talk) 19:25, 24 January 2011 (UTC)

I guess it arises from trying to teach matrices before people have learnt the basics of groups, rings, fields and vector spaces. That is the proper context. From years of teaching this naively, the only way of justifying matrix multiplication seemed to be in terms of substituting one set of linear equations into another. 51kwad (talk) 13:29, 27 January 2011 (UTC)

People have been doing matrix multiplications well before the definition of groups, rings, fields, and vector spaces were even conceived. And they did so without bridges and buildings crumbling. Angry bee (talk) 03:29, 18 March 2012 (UTC)

The article is definitely focused upon too narrow an audience. It's not that it's too technical, it's that it lacks a basic explanation of what matrices are and what they might be used for. The article also meanders around to topics that really don't belong here, such as various algorithms for computational efficiency. Obviously such algorithms should have there own articles and do nothing to explain what matrices are.

It's almost humorous that the article is so long and goes into such depth about how to compute matrices, but completely misses why you might want to do so. Gatohaus (talk) 14:55, 1 February 2011 (UTC)

Er… Which article are you commenting on? Obviously, the explanation of what matrices are belongs to the article matrix (mathematics), and not the article on matrix multiplication; an explanation of why you might want to multiply matrices occurs in the second sentence of the lead, and then again in the second sentence of the first section. Where I agree with you is that algorithms for efficient computation of the matrix product should eventually be spawned off. Arcfrk (talk) 01:32, 2 February 2011 (UTC)

Thinking the low grade and overtechnicality could be solved if matrix multiplication could have a disambiguation page and separate, better articles for different depths of the material. One article for multiplication of matrices with real values with applications to linear algebra, and another one with abstract algebra considerations and more advanced concepts. Matrix multiplication is used in different contexts. Formally it is not ambiguous but in human understanding it is. Wikivek (talk) 21:11, 9 February 2011 (UTC)

No, I disagree. There is no need to write a second article (and doing so would actually harm both resulting articles). Instead, this article here should start out with a section taking two concrete matrices (with integer entries, say) and calculating their products. It is also conceivable to make an example of multiplication of two 2-by-2 matrices, and relating the product to the composition of the corresponding linear maps. Jakob.scholbach (talk) 21:23, 9 February 2011 (UTC)

I also oppose splitting the article. The article needs to be more accessible especially at the beginning. The article could be improved by bringing in some of the text from the matrix article. --Kvng (talk) 15:25, 11 February 2011 (UTC)

The article is indeed too technical. Let's simplify a step at a time, for example, the second sentence of the summary is already covered in the content and doesn't add anything to summarize what the article is about. It will confuse anyone if they jump to those topics which are way beyond matrix multiplication. Also, the first part of the content shouldn't be implying that the reader jump to topics on Linear Transforms or vector spaces...it should give the reader some insight into what matrix multiplication does...not a technical reason for why it's possible. Rockn-Roll (talk) 14:08, 7 March 2011 (UTC)

re-write

I re-wrote the article. See also here. Please do not revert anything,

1. I removed most of the colours since they were too bright, and doesn't help colour-blind people understand what's going on. It’s on anyone who wants to add the colour back, sorry but was not that brilliant.
2. tried to make it more understandable,
3. add sources,
4. use the superficially (at least in my experience) standard notation on lowercase bold for vectors, capital bold for matrices.
5. A few things such as the mix of italic with bold for matrices was a reoccurring theme,
6. some notations didn't comply with WP:MOSMATH (like the matrix transpose),
7. the wording in places was very ambiguous for a layman.

F = q(E+v×B) ⇄ ∑_ic_i 01:25, 8 April 2012 (UTC)

I'm guessing there may be some reaction to my removal of colours, I may add them back eventually, but let’s not have burning, monochromatic LaSeRs in our eyes. Let’s have neatly and readable typeset LaTeX instead... F = q(E+v×B) ⇄ ∑_ic_i 09:16, 8 April 2012 (UTC)

Meaning

I do not understand the meaning of the first expression in: $\lambda (A)_{ij}=(\lambda A)_{ij}=\lambda A_{ij}\,\!$— Preceding unsigned comment added by Nijdam (talk • contribs)

In words the first two can be expressed as "the scalar multiple of any element equals the matching element of the matrix obtained by multiplying that scalar times the matrix". The third is a consequence of this observation, as because the multiplication can be done before or after extracting the matrix element it doesn't matter where the brackets go so they can be omitted, as in associative products.--JohnBlackburne^words_deeds 19:02, 8 April 2012 (UTC)

Frobenius inner product?

Is the Frobenius inner product a way "to multiply two matrices and get another"? No. Its a sum of matrix elements (of the Hadamard product) so why include it in this article? For now it has been subsubsectioned into the Hadamard product, but really should be moved to somewhere else. It hasn't its own article but perhaps the better place would be here? Maschen (talk) 09:37, 9 April 2012 (UTC)

I also included a mention of what the Kronecker product is and linked it, since that is a way to multiply two matrices and get a third. By rights this should be a subsection rather than the Frobenius inner product.Maschen (talk) 09:38, 9 April 2012 (UTC)

Good point and nice editing. You're right, but the link you give is about Matrix norms, not inner products (norms are consequences of inner products). For this article it may be simpler and easier demote the subsubsection to the Hadamard product subsection and just state it’s "the sum of elements of the Hadamard product", keeping the same link. Good to include the Kronecker product also. F = q(E+v×B) ⇄ ∑_ic_i 10:05, 9 April 2012 (UTC)

Perhaps the definition "to multiply two matrices and get another" is too restrictive, then, or alternatively you could consider the result as a 1-by-1 matrix. The dot product is a product of two vectors, and the Frobenius product is an analogous operation for matrices, so saying that it's not a way to multiply matrices would be strange. Also, the ordinary matrix product of a row vector and a column vector is essentially the same as the dot product of the vectors, and whether you consider that to be a 1x1 matrix or a scalar usually varies based on whatever is convenient for the purpose (it certainly won't take much digging to find expressions in the wild where the dimensions won't match if you strictly interpret such things as 1x1 matrices!). You can convert the Frobenius product of A and B to the product of a row and column matrix by expressing it as vec(A)^Tvec(B), inheriting the same ambiguity. -- Coffee2theorems (talk) 22:11, 11 July 2012 (UTC)

Many examples... so removed one

I removed at least the last one called "Rectangular matrices" the lead section Matrix product (two matrices), since it abruptly introduces numbers and letters (contrary to the more followable and systematic choice of entries) and is too long, and there are enough examples in the article without it anyway. A matrix product including (slightly) larger dimensions is already below in the section The inner and outer products. The important thing is that readers have the general definition, and recive the idea of multiplying elements along the rows in the first matrix and down the columns in the second, and the row and column number is the entry in the final matrix. There is also the illustration. Hence removed the longer example. Maschen (talk) 11:09, 9 April 2012 (UTC)

Fair point, the reason I included the extra example was to show what it would be like for entries which are not systematic (like all the other examples) since in a real calculation the numbers are not usually a nice and neat pattern, and larger sized matrices around 3/4 rows/columns. Then since this as an encyclopaedia it should state more of what matrix multiplication is with a minimum number of examples, so the removal is fine, I agree now anyway. Nice work in extending the other example in the section The inner and outer products [2], since it was abrupt. =)F = q(E+v×B) ⇄ ∑_ic_i 11:32, 9 April 2012 (UTC)

diagrams (again)

Maschen, I think you should update the image you had (the "one on the left" with a spiral/coil like "mental path", now in the archive, not the "one on the right" with a "wavy mental path") to the notation in the article, and add it. I think it helps, just because there was one opinion against it doesn't make it wrong. For the caption: just write "The arithmetic process of multiplying row i in matrix A and column j in matrix B." Don't repeat those words in the image, just keep the arrows and "spiral/coil" path. Change the colours too, those look drab and dull.

If anyone objects and deletes when its added to the article, then of course it can be debated then. =) F = q(E+v×B) ⇄ ∑_ic_i 11:58, 9 April 2012 (UTC)

I didn't have any hope for it, but at your request and suggestions which may amplify its meaning, I'll try. I'll use the colour scheme of blue/yellow, since red, yellow, blue are in the article. Good caption also. I'll not write any words (also allows it to be used in other languages than English, if it is used). Maschen (talk) 12:01, 9 April 2012 (UTC)

Here it is:

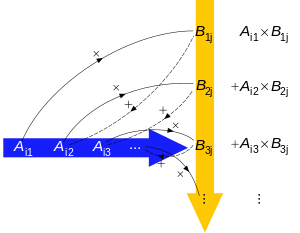
any better? Maschen (talk) 12:16, 9 April 2012 (UTC)

Much better! Thanks and well done. Add it to the subsection General definition in Matrix product (two matrices) with the caption I suggest (or words to that effect). =) F = q(E+v×B) ⇄ ∑_ic_i 12:19, 9 April 2012 (UTC)

Thank you. Your caption is as simple as it gets, so if I could use it I am very grateful. Here it goes... Maschen (talk) 12:31, 9 April 2012 (UTC)

Done. I extended the caption slightly. You may have to refresh the browser to see a change in colour also. Anyone who dislikes it can say so here. Maschen (talk) 12:45, 9 April 2012 (UTC)

Nice work. =) It'll be interesting to see how many people come here complaining how "unreadable/unclear/confusing" the article is now, given the mass re-transform from what it was a couple of days ago... F = q(E+v×B) ⇄ ∑_ic_i 12:48, 9 April 2012 (UTC)

Left Multiplication vs. Right Multiplication

There are a couple of points in this article which specify the handedness of the multiplication; I think some explanation should be provided--or at least a reference/link to somewhere to look for that. All Clues Key (talk) 05:19, 3 September 2012 (UTC)

Do you mean left and right scalar multiplication? That's pretty obvious and clear from the article. The handedness of matrix multiplication is partially discussed throughout, in particular the properties section where non-commutativity is stated. (Apologies that no-one has replied for 20 days!)... Maschen (talk) 11:04, 23 September 2012 (UTC)

I tried to clear it up [3] in the properties section, hope it's ok. Maschen (talk) 11:17, 23 September 2012 (UTC)

Archive 1

Assessment comment

The comment(s) below were originally left at Talk:Matrix multiplication/Comments, and are posted here for posterity. Following several discussions in past years, these subpages are now deprecated. The comments may be irrelevant or outdated; if so, please feel free to remove this section.

Article needs a lead. Geometry guy 22:04, 9 June 2007 (UTC) More than that, it's one of the most linked articles on math wikipedia, and all it sets out to do is to review different ways of multiplying matrices? Needs much broader frame. Arcfrk 07:50, 28 June 2007 (UTC)

Last edited at 07:50, 28 June 2007 (UTC). Substituted at 06:33, 7 May 2016 (UTC)

Recent addition of section: Matrix_multiplication#Multiplication_of_n-dimensional_matrix

This section has unsourced content which is maybe not immediately recognizable. The English is also a little broken, along with a bit of the organization. I think the section is badly in need of a haircut and some citations, if it is going to remain. Rschwieb (talk) 14:16, 6 March 2013 (UTC)

(edit conflict)Is "multidimensional arrays" the best terminology? "N-dimensional matrices" usually refers to a n × n square matrix (which in the terminology of the new section means a 2d matrix... which may confuse people)? Rschwieb and myself asked the editor on his/her talk page. M∧Ŝc²ħεИ_τlk 14:22, 6 March 2013 (UTC)

I've removed the section. If this is not complete original research, then to be treated in the main article on the topic of matrix multiplication would obviously require very good sources (WP:WEIGHT). As it stands, the proposed matrix product seems to be completely novel. If it is studied in the literature, then sources are needed to determine where and how an encyclopedia can deal with the topic. Sławomir Biały (talk) 22:50, 6 March 2013 (UTC)

Fine enough, wasn't sure if it was OR. M∧Ŝc²ħεИ_τlk 23:03, 6 March 2013 (UTC)

You can have tensors with more than two indices, and contract over several of those indices at once. Does that relate to anything in the deleted section? Jheald (talk) 22:44, 7 March 2013 (UTC)

I tried to relate it to tensor contraction, but failed. It involves a cyclic permutation of indices in addition to the contractions. The product ends up being non-associative, even for powers of a single matrix. Tensors are also defined by their transformation properties under a coordinate change and, IIRC, there was no mention of transformation properties in the section. --Mark viking (talk) 23:07, 7 March 2013 (UTC)

Ideas for Improvement

Does anyone know why this page is still rated C-level? What do people want to see in an improved version?Sbenzell (talk) 19:53, 7 April 2013 (UTC)

I am no expert on article rating, but in my opinion, the lead is completely inadequate in introducing matrix multiplication, giving the reader context, or in summarizing the article. There are relatively few citations and some sections have no citations at all. There is no history section. Check out Wikipedia:Good article criteria as a guide to what editors look for in a good article. --Mark viking (talk) 22:01, 7 April 2013 (UTC)

History and citations are always nice. But the lead does say what matrix multiplication is, and states clearly enough that there is more than one way to multiply matrices, although an extension would be fitting I simply don't know how... M∧Ŝc²ħεИ_τlk 22:35, 7 April 2013 (UTC)

I'd like to say that regardless of this page's rating as a "Wikipedia page" it is fantastic as an educational tool. It has explained matrix products perfectly for me -- where most maths wiki pages seem to completely smother the reader in unexplained jargon. — Preceding unsigned comment added by 94.171.250.70 (talk • contribs), 2013-07-02T21:44:14

The article is still rather incomplete and sources are still lacking, but at least now we have a lead section. Hope my resectioning is not controversial.

Sbenzell's question should be repeated: apart from sources and a history section (and the empty sections I introduced, not inclined to fill them in for now), what more could be improved or added? M∧Ŝc²ħεИ_τlk 17:37, 5 January 2014 (UTC)

I would strongly recommend a section on "applications", to mention different fields of study which rely on matrix multiplication, or to at least provide some real-life examples. Right now it's just abstract mathematics. MM (talk) 00:07, 30 April 2015 (UTC)

From the German Wikipedia article: Application areas of matrix multiplication include computer graphics (graphics pipeline), optics (ray transfer matrix analysis), economics (input–output models), robotics (Denavit–Hartenberg parameters), electrical engineering (network analysis) and quantum mechanics (matrix mechanics). Matrix powers have further applications, e.g. in graph theory (shortest path problem) and population dynamics (Leslie matrix). Best wishes, --Quartl (talk) 06:13, 30 April 2015 (UTC)

Sources for a history section

Let's compile them here:

General

• "When was Matrix Multiplication invented?".
• J. Schneider (2001). "How Matrices Began..."

Computation, algorithms

• Virginia Vassilevska (2008). Efficient Algorithms for Path Problems in Weighted Graphs. ProQuest. ISBN 0-549-758-852.

The book may be OK, less sure about the webpages... Feel free to add to the list. M∧Ŝc²ħεИ_τlk 11:49, 12 July 2013 (UTC)

I've just added Binet as the inventor to the lead of the article, with MacTutor as the source, without seeing this section. Feel free to revert if you don't trust MacTutor. QVVERTYVS (hm?) 22:43, 22 October 2013 (UTC)

I'm afraid I do not consider MacTutor reliable. However, I'm not an expert in math history. — Arthur Rubin (talk) 10:17, 23 October 2013 (UTC)

Agreed MacTutor is not reliable for WP. It's pretty hard to find reliable sources on the history of matrix multiplication - every book I've seen on matrix algebra or linear algebra seem to just define the matrix operations without providing any historical background. M∧Ŝc²ħεИ_τlk 15:47, 23 October 2013 (UTC)

Matrix powers and discrete difference equations

Matrix powers of the form $A^{t}$ are useful for solving linear difference equations look like:

$x_{t+1}=Ax{t}+Bu(t)$,

where $x(t)$ is the state space, $u(t)$ is the input, $A$ is the state-space matrix, and $B(t)$ is the input matrix.

This method was taught to me by a Hungarian mathematician and I'm not even sure what it is called. The problem is to find $A^{t}$.

Anyways I will include an example and steps below. Given $A={\begin{pmatrix}1&1&0&0\\0&1&1&0\\0&0&1&-1/8\\0&0&1/2&1/2\end{pmatrix}}$

First, compute the eigenvalues. $\lambda _{1}=3/4$ and $\lambda _{2}=1$ each with an algebraic multiplicity of two.

Now, take the exponential of each eigenvalue multiplied by $t$: $\lambda _{i}^{t}$. Multiply by an unknown matrix $B_{i}$. If the eigenvalues have an algebraic multiplicity greater than 1, then repeat the process, but multiply by a factor of $t$ for each repetition. If one eigenvalue had a multiplicity of three, then there would be the terms: $B_{i_{1}}\lambda _{i}^{t},B_{i_{2}}t\lambda _{i}^{t},B_{i_{3}}t^{2}\lambda _{i}^{t}$. Sum all terms.

In our example we get:

$A^{t}=B_{1_{1}}\lambda _{1}^{t}+B_{1_{2}}t\lambda _{1}^{t}+B_{2_{1}}\lambda _{2}^{t}+B_{2_{2}}t\lambda _{2}^{t}$

$A^{t}=B_{1_{1}}(3/4)^{t}+B_{1_{2}}t(3/4)^{t}+B_{2_{1}}1^{t}+B_{2_{2}}t1^{t}$.

So how can we get enough equations to solve for all of the unknown matrices? Increment $t$.

${\begin{aligned}IA^{t}=&B_{1_{1}}(3/4)^{t}+B_{1_{2}}t(3/4)^{t}+B_{2_{1}}+B_{2_{2}}t\\AA^{t}=&B_{1_{1}}(3/4)^{(t+1)}+B_{1_{2}}{(t+1)}(3/4)^{(t+1)}+B_{2_{1}}+B_{2_{2}}{(t+1)}\\A^{2}A^{t}=&B_{1_{1}}(3/4)^{(t+2)}+B_{1_{2}}{(t+2)}(3/4)^{(t+2)}+B_{2_{1}}+B_{2_{2}}{(t+2)}\\A^{3}A^{t}=&B_{1_{1}}(3/4)^{(t+3)}+B_{1_{2}}{(t+3)}(3/4)^{(t+3)}+B_{2_{1}}+B_{2_{2}}{(t+3)}\end{aligned}}$

Since the these equations must be true, regardless the value of $t$, we set $t=0$. Then we can solve for the unknown matrices.

${\begin{aligned}I=&B_{1_{1}}+B_{2_{1}}\\A=&(3/4)B_{1_{1}}+(3/4)B_{1_{2}}+B_{2_{1}}+B_{2_{2}}\\A^{2}=&(3/4)^{2}B_{1_{1}}+2(3/4)^{2}B_{1_{2}}+B_{2_{1}}+2B_{2_{2}}\\A^{3}=&(3/4)^{3}B_{1_{1}}+3(3/4)^{3}B_{1_{2}}+B_{2_{1}}+3B_{2_{2}}\end{aligned}}$

This can be solved using linear algebra (don't let the fact the variables are matrices confuse you). Once solved using linear algebra you have:

${\begin{aligned}B_{1_{1}}=&128A^{3}-336A^{2}+288A-80I\\B_{1_{2}}=&{\frac {64}{3}}A^{3}-{\frac {176}{3}}A^{2}+{\frac {160}{3}}A-16I\\B_{2_{1}}=&-128A^{3}+336A^{2}-288A+81I\\B_{2_{2}}=&16A^{3}-40A^{2}+33A-9I\end{aligned}}$

Plugging in the value for $A$ gives:

${\begin{aligned}B_{1_{1}}=&{\begin{pmatrix}0&0&48&-16\\0&0&-8&2\\0&0&1&0\\0&0&0&1\end{pmatrix}}\\B_{1_{2}}=&{\begin{pmatrix}0&0&{\frac {16}{3}}&-{\frac {8}{3}}\\0&0&-{\frac {4}{3}}&{\frac {2}{3}}\\0&0&{\frac {1}{3}}&-{\frac {1}{6}}\\0&0&{\frac {2}{3}}&-{\frac {1}{3}}\end{pmatrix}}\\B_{2_{1}}=&{\begin{pmatrix}1&0&-48&16\\0&1&8&-2\\0&0&0&0\\0&0&0&0\end{pmatrix}}\\B_{2_{2}}=&{\begin{pmatrix}0&1&8&-2\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{pmatrix}}\end{aligned}}$

So the final answer would be:

${A}^{t}={\begin{pmatrix}1&t&{\frac {\left(24\,t-144\right)\,{2}^{2\,t}+\left(16\,t+144\right)\,{3}^{t}}{3\,{2}^{2\,t}}}&-{\frac {\left(6\,t-48\right)\,{2}^{2\,t}+\left(8\,t+48\right)\,{3}^{t}}{3\,{2}^{2\,t}}}\\0&1&-{\frac {\left(4\,t+24\right)\,{3}^{t}-3\,{2}^{2\,t+3}}{3\,{2}^{2\,t}}}&{\frac {\left(2\,t+6\right)\,{3}^{t}-3\,{2}^{2\,t+1}}{3\,{2}^{2\,t}}}\\0&0&{\frac {\left(t+3\right)\,{3}^{t-1}}{{2}^{2\,t}}}&-t\,{2}^{-2\,t-1}\,{3}^{t-1}\\0&0&t\,{3}^{t-1}\,{2}^{1-2\,t}&-{\frac {\left(t-3\right)\,{3}^{t-1}}{{2}^{2\,t}}}\end{pmatrix}}$

This method was taught as it is nearly the same procedure to calculate $exp(At)$ (useful for linear differential equations). Except that instead of incrementing $t$ to get additional equations and using $\lambda _{i}^{t}$ in the terms, one takes the derivative with respect to $t$ to generate additional equations and using $e^{(\lambda _{i}t)}$ in the terms.Mouse7mouse9 05:38, 7 December 2013 (UTC)

I made a package for the computer algebra system Maxima, it is still under development but can be found here (https://github.com/Mickle-Mouse/Maxima-Matrix-Power). It handles repeated zero eigenvalues and repeated nonzero eigenvalues using tricks similar to Buchheim's generalization of Sylvester's formula, except in a discrete domain. To see this trick used in its appropriate context see (https://en.wikipedia.org/wiki/Talk:Matrix_exponential#A_method_I_was_taught.2C_but_cannot_find_external_references).Mouse7mouse9 23:21, 29 December 2013 (UTC) — Preceding unsigned comment added by Mouse7mouse9 (talk • contribs)

The method seems unnecessarily complicated. Why not go directly from:

$A^{t}=B_{1_{1}}(3/4)^{t}+B_{1_{2}}t(3/4)^{t}+B_{2_{1}}1^{t}+B_{2_{2}}t1^{t}$.

to

${\begin{aligned}I=&B_{1_{1}}+B_{2_{1}}\\A=&(3/4)B_{1_{1}}+(3/4)B_{1_{2}}+B_{2_{1}}+B_{2_{2}}\\A^{2}=&(3/4)^{2}B_{1_{1}}+2(3/4)^{2}B_{1_{2}}+B_{2_{1}}+2B_{2_{2}}\\A^{3}=&(3/4)^{3}B_{1_{1}}+3(3/4)^{3}B_{1_{2}}+B_{2_{1}}+3B_{2_{2}}\end{aligned}}$

? In any case, I am almost certain it is published somewhere, and it's not really contentious, so I might be in favor of inclusion. Would it help if I posted the methods somewhere on the Internet, noting that my expertise would make it allowable under WP:SPS, until such time as a (normally) published reliable source can be found? — Arthur Rubin (talk) 02:27, 30 December 2013 (UTC)

@Mouse7mouse9: why do you think this is relevant or useful to an introductory article on the variety of matrix multiplications? As it stands it looks like WP:OR (feel free to contradict me with sources). M∧Ŝc²ħεИ_τlk 13:02, 5 January 2014 (UTC)

@Maschen:Perhaps you are correct Maschen. This is more useful as an application for solving discrete linear systems. So I made a cross post to the talk section for the recurrence relation page. https://en.wikipedia.org/wiki/Talk:Recurrence_relation#A_method_for_discrete_linear_systems.

Sorry for such a late response - my previous comment probably had a negative tone, I appreciate your good faith addition. Unfortunately for now I don't have the time and expertise to look through it in detail. Thanks for posting on the right talk page too. M∧Ŝc²ħεИ_τlk 23:20, 18 February 2014 (UTC)

New asymptotic complexity by Le Gall (2014)

Cited from the lead of Coppersmith–Winograd algorithm:

In 2014, François Le Gall simplified the methods of Williams and obtained an improved bound of O(n^2.3728639).

The section Matrix multiplication#Algorithms for efficient matrix multiplication should be updated accordingly, by an expert. Also, the picture File:Bound on matrix multiplication omega over time.svg should be updated, by someone who has installed Mathematica. - Jochen Burghardt (talk) 18:30, 27 June 2014 (UTC)

I updated the text, but I don't have Mathematica so someone else needs to do that part. Le Gall's paper is appearing in ISSAC 2014 so it should count as a reliable source (the version previously cited on the Coppersmith–Winograd article was just a preprint). —David Eppstein (talk) 20:59, 27 June 2014 (UTC)

This page fails to compile to pdf.

Error:

Generation of the document file has failed. Status: Rendering process died with non zero code: 1 — Preceding unsigned comment added by Vrbatim (talk • contribs) 05:54, 13 February 2015 (UTC)

I see the same thing. Conversion of other articles (at least the one I tried) works. YohanN7 (talk) 01:52, 14 February 2015 (UTC)

Could someone explain what PDF compilation process is being referred to here? I was unaware that WP provided such a feature. The statement of the problem is rather ... cryptic. —Quondum 02:19, 14 February 2015 (UTC)

"Download as PDF" is available in the menu (on the left if you have the same skin as I have). Nice feature when it works. YohanN7 (talk) 03:48, 14 February 2015 (UTC)

Okay, thanks, I had not noticed that before. Sorry for the confusion. —Quondum 04:23, 14 February 2015 (UTC)