Talk:Lagrange point/Archive 1

Archive 1

Archive 2

Arbitrary section header

Perhaps someone could generate a diagram of the various points?

---

While I was staring at the lagrange points diagram, I realized that the diagram resembles a large "peace sign". Has anyone noticed this? I wonder if the concept of "balance" (of gravity) that the lagrange points represent was borrowed to also represent peace.

Does anyone have any knowledge in this area? What do you think about adding a short sentence or two on this resemblance?

- Jamie E (USA)

Jamie, your question is a common one but the resemblance between the Lagrange point diagram and the peace symbol is only coincidental. The peace symbol is a superposition of the flag semaphore symbols for 'N' and 'D' and form the acronym "ND" for *N*uclear *D*isarmament. That these two semaphore symbols for N and D were encircled is no mystery either as many sigils exploit the symbolism of the circle, and the peace symbol was certainly an embodiment of the peace movement as such. Cheers, Astrobayes 04:54, 15 July 2006 (UTC)

---

That would be lovely, but I'm restricted to ASCII here and I'm not about to start fiddling with slashes and backslashes and capital letter O's all afternoon :P -- Paul Drye

Not exactly what you had in mind, I know - but I wondered if this would be any good for the page (it's NASA so presumably public domain, I havent seen anything contradicting that posted anywhere) - http://map.gsfc.nasa.gov/m_ig/990529/990529b.jpg --Si42 01:10, 31 January 2006 (UTC)

Template:PD-USGov-NASA says it is okay, and I think it'd be a useful picture to have, for instance in the Stability section. -- Jitse Niesen (talk) 15:42, 31 January 2006 (UTC)

---

The paragraph

The Earth's companion object Cruithne is in a somewhat Trojan-like orbit around the Earth, but not in the same manner as a true Trojan. It has a regular solar orbit that is bumped at times by Earth. When the asteroid approaches Earth, the asteroid takes orbital energy from Earth and moves into a larger, higher energy orbit. When the asteroid (in a larger and slower orbit) is caught up by Earth, Earth takes the energy back and so the asteroid falls into a smaller, faster orbit and eventually catches Earth to begin the cycle anew. Epimetheus and Janus, satellites of Saturn, have a similar relationship, though they are of similar masses and so actually exchange orbits periodically.

is fascinating information, but has nothing to do with Lagrangian points or Trojan objects. Whither should it be moved?

Maybe to asteroid? --AN

Which class of asteroids is Cruithne in and do we have a page for it?

---

Put back in the "but differing" that Xaonon took out. It's a critical part of the definition!

Are you sure? I'm fairly certain that two equal masses orbiting each other would result in libration points as well -- a binary star system, for example. -- Xaonon

Well, technically you get them, but without the mass difference you lose the fundamental quality of an L-point: stability. Unless...

• Mass A is "substantially" larger than mass B -- by about a factor of 30.
• Mass C, at the libration point, has essentially no mass in comparison to both A and B.

...the points aren't linearly stable and can't hold anything. Basically, the centre of gravity of the system must be pretty close to A or it doesn't work. See J.M.A. Danby's "Fundamentals of Celestial Mechanics" (I think) where the ratio is discussed. -- Paul Drye

---

Take "differing" out! Even if the above is true (which I doubt, at least for L1, L2, & L3), the intro makes no sense with "differing" when you consider the two "slightly differing" cases. It would have you believe the L points vanish at the point mass equality is passed. It's just nonsense.

And the idea in the intro that two masses combine to form L points is just lousy English, which amounts to more nonsense if you don't read between the lines.

And the intro fails to mention the important point that bodies at the L points are not at all in equilibrium, unless they have a certain velocity. Such bodies must be inserted into their L orbits as any orbital body must be.

This is my first and last contribution to the Wikipedia, as I see below that contributions must be licensed under the GNU FDL, which has proprietary features that require me to be less liberal than I normally care to be.

---

Very good article, but I think the explanation as to why L1 L2 and L3 are unstable compared to L4 and L5 needs to be clearer. If you map the gradient fields for these points you'll notice that L1 L2 and L3 are at the top of hills but L4 and L5 are at the bottom of a depression, im not sure why that is but I think it is an expanation as to why objects would stay in their holes.--ShaunMacPherson 07:11, 10 Mar 2004 (UTC)

No, L1-3 are at saddle points in the pseudopotential field, while L4, L5 are at the tops of hills. (follow the external link to a pretty picture of the field.) Objects at 1-3 can just wander off, while staying at the same level. Objects at 4 and 5 fall down the hills, but then the Coriolis force kicks in, and keeps them in orbit around the Trojan points. –– wwoods 09:34, 25 Mar 2004 (UTC)

---

In Lagrangian mechanics, a Lagrangian point is…

I changed this opening sentence to In celestial mechanics…, basically because:

1. The old definition suggested that Lagrange points emerge uniquely in Lagrangian mechanics. But Lagrange points are a physical phenomenon, independent from the theories or formalisms you use. They exist in Newtonian mechanics and in general relativity just as well.
2. While not actually a tautology to the insider, it may look confusingly so to an outsider. The old definition might have been true, but didn't really explain anything.
3. It makes sense to define a concept in the context of a wider, more generally known concept. Celestial mechanics meets that criterion better than Lagrangian mechanics does.

—Herbee 00:15, 2004 Mar 20 (UTC)

---

An asteroid was discovered to be in Neptune's L4 point. I was wondering if someone could work it into the part talking about similar systems? The asteroid's name is 2001 QR322, and I just created a page for it. --Patteroast 16:50, 15 Jun 2004 (UTC)

---

Can anyone answer a hypothetical question for me? If one had two super massive bodies of precisely equal mass orbiting about each other, would they generate Lagrange points as described here? I suspect that the positions of L1, L2 and L3 will be similar, but will L4 and L5 still be at the 60Deg Trojan points?

Thanks in advance, PBA

Yes, a system of two equal masses (they don't have to be "super massive") orbiting around their common center of mass will have all five Lagrange points. However the L4 and L5 points will be unstable. They will also be in a much higher orbit than the masses. If the masses are at a distance r from the CM, then the L4/5 points will be ${\sqrt {3}}r\approx 1.7r$ from the CM.
--wwoods 19:07, 23 Jun 2004 (UTC)

---

So how does the rest of the solar system fit in? I mean it's all very well to speak of a 3 body system, but for all practical purposes, the other planetary bodies are going to interact with as well. How does that affect the relative stability of, for examaple, the Terra-Sol Lagrange points, or the Luna-Terra L-points? Is this possible effect the reason why one hears L5 advanced as a site for a sizable space habitat? Or is that due to some literary influence of which I am ignorant?

Yes, the presence of other masses in the real Solar System perturbs bodies at the L4 and L5 points, but obviously not too much, as evidenced by the presence of objects at various L4&5 points around the system.

L5 was proposed as a habitat site because the stability reduces the need for station-keeping, and because it was close to the Moon in terms of delta v (~0.7 km/s).

—wwoods 17:44, 21 Aug 2004 (UTC)

Coriolis effect

I'm unhappy with invoking the Coriolis effect for explaining why a point is stable. The Coriolis effect is merely a device to explain the apparent deviation of a free moving object when viewed from a rotating frame of reference. It cannot really explain the stability of a Lagrange point. What says anyone? Paul Beardsell 23:46, 23 August 2005 (UTC)

Nuthin'. Paul Beardsell 00:53, 5 September 2005 (UTC)

I realize that this point is a bit belated, but classifying L4 and L5 as "unstable" is done by looking at an effective potential for the two body system in a rotating reference frame. However, this effective potential doesn't take into account the existance of the Coriolis forces in this reference frame. Thus, the Coriolis forces effectively cause these points to be stable, when we are looking at it in a rotating reference frame. Unfortunately, to look at this problem in an inertial reference frame would be technically quite difficult, although perhaps conceptually clearer, since you don't need to invoke centrifugal or Coriolis forces. If you did do the problem in the inertial frame, you would see that the Lagrange points (Lagrange orbits, if you will) would be stable, in the sense that a small perturbation from the Lagrange orbit would effectively cause epicyclic motion about the circular Lagrange orbit. Grokmoo 04:24, 1 March 2006 (UTC)

needs pronounciation

This article needs a sentence about how to pronounce it. Is the g hard or soft (for both of them)?

Thanks for your comment. The first g is pronounced as in go, the second as in judge. I added the pronunciation in IPA. -- Jitse Niesen (talk) 12:45, 4 September 2005 (UTC)

Wrong in L2 Examples?

I got another value for the example values on the L2 point. Sun-earth OK: 1.5*10^6km from earth Moon-earath : 65348 km

Maybe due to measuring from surface and center. Nor my source, nor wiki specifices. However centre would make more sense, don't you think.

I also get (distance from earth): L1 sun-earth: 1.49*10^6km L3 sun earth: 2.992*10^8km

I also get (distance from moon): L1 sun-earth: 57660km L3 sun earth: 764956km

wrong example?

"Earth–Moon L2 would be a good location for a communications satellite covering the Moon's far side."

no it wouldn't. how would you send information to it? isn't the moon in the way? I did not remove the sentence yet. —The preceding unsigned comment was added by 212.120.85.242 (talk • contribs) .

Satellites operating "at" collinear libration points (such as L2) are generally not actually located at the point, but rather in a halo or lissajous orbit around the point. If the amplitude of this periodic orbit is sufficiently large then the spacecraft will always have line-of-sight to the Earth. --Allan McInnes (talk) 05:22, 1 March 2006 (UTC)

Especially line-of-sight to a comms array in geostationary orbit around the earth.--Si42 19:45, 15 April 2006 (UTC)

Allan, you should add your explanation to the article, since I wondered the same thing when I read the example. --euyyn 00:43, 13 May 2006 (UTC)

Deleted false sentence

I deleted this sentence from the first picture's caption since it's nonsense to me:

An object in free-fall would trace out a contour (such as the Moon, shown).

Just look at the sharpness of the contours near L1: an object in free-fall could never do those movements, since the centre of the (fictional) centrifugal force isn't at L1, but at the centre of masses of the Sun and the Earth. In addition, free-falling objects can perfectly have elliptical orbits, thus crossing several contours. So the sentence is false in every posible way it could be. --euyyn 00:43, 13 May 2006 (UTC)

L4/L5 explanation using only gravity and 'centrifugal' force?

The examples given under L1/2/3 nicely explain, imho, the existence of these points from the simple addition (cancellation) of the gravitational fields and the centrifugal force. But I notice there is no such explanation under the L4/5 points. Can someone who understands these points add in a similar example/explanation? If it were possible for a body to sit at exactly the top of the potential hill at L4/5 , then it seems to me that one could remove the Earth and that body would stay in exacly the same position and same orbit. This implies that the presence of the Earth for a body at these points of irrelevent..but I don't understand how that can be as adding the additional force of the Earth would surely drag the body out of its circular orbit about the Sun. Anyway, I'm just looking for a clearer physical picture using only gravity/centrifugal force to explain the L4/5 points. Thanks!

You need the coriolis force to explain them.... This link http://map.gsfc.nasa.gov/m_mm/ob_techorbit1.html has some good info (most of this page seems to be sourced from it) & if you know some maths you could download the pdf & have a look at it. 203.97.255.167 00:14, 3 September 2006 (UTC)

Third pronunciation

I pronounce "Lagrangian" as [ləˈgɹe(ɪ)n.dʒiˌʊn]. Does anyone else?  Denelson83  00:28, 12 June 2006 (UTC)

Yeah. do that too. Is that a "mispronunciation"? AEuSoes1 06:39, 24 August 2006 (UTC)

Fictional References

I was delighted to finally read a clear explanation of the L4 and L5 points as they are extensively used in the Transhuman Space roleplaying game. This includes the Trojans and the L4 and L5 points around Earth. I suppose this goes under the mention made of hard science, but I thought I might as well mention it. - Philippe J (FR)

Just noticed that the Peter F. Hamilton, Nights Dawn, refernce is incorrect. This occurs in the first book, The Reality Dysfunction, as part of the battle for Lalonde. p 1172-73 and 1189-94 in the 1997 Pan Books paperback edition. The episode in the second book involves making a gas giant go nova to create a debris front that the Lady Mac would be in front of, and the pursuing starship would be caught by.

stability of L4/L5

Aren't L4 and L5 stable points in the Earth-Sun model? The blue arrows in de picture show them as instable, which I think is incorrect. --Mushlack 17:32, 2 August 2006 (UTC)

They are potential peaks, hence the blue downwards-slope arrows. They are, as you say, stable, even though the potential diagram does not show it. It requires slightly more sophisticated maths... 203.97.255.167 00:15, 3 September 2006 (UTC)

Kordylewski cloud at Earth-Moon L4/L5

There are supposed to be coulds of dust at both of this points. Does anybody have any specific details how much dust there is (or if there even is dust there) in stable halo orbit? Since this orbit is the size of the earth this could have large combined mass (enough to collect and use?) or could pose a problem to any object in it's halo orbit. --Taho s 18:49, 24 February 2007 (UTC)

Lagrange points over time

Over a period of time, do Lagrange points change as the objects, such as earth, continue in their orbits?

And also, the equations and the points seem to be based on a circular orbit, wouldnt the Lagrangian points be different using the elliptical orbits that planets truly move in? Xlegiofalco 06:34, 22 November 2006 (UTC)

The Lagrange points would only change if the orbits themselves change. And as long as the eccentricity is low enough (I'm not sure what the cutoff point would be, I suspect it varies depending on mass and other factors), the same principle holds, although it would create somewhat more complex orbits, I believe Nik42 01:31, 26 May 2007 (UTC)

Please, re-check info on the page

This page and the one on the Advanced Composition Explorer contradict each other about the satellite's orbit. This page informs that ACE is kept on Lissajous orbit and ACE's page tells about an Halo orbit.

Can someone correct either?

--Dr. Pnz 04:11, 21 January 2007 (UTC)

"In orbit around" L2?

Is it correct to describe the satellite as being "in orbit around" the L2 point here:

"The Wilkinson Microwave Anisotropy Probe is already in orbit around the Sun–Earth L2."

Maybe they're two separate statements: "The probe is already in orbit" and "The probe is around (near) L2".--Nonpareility 22:43, 30 January 2007 (UTC)

It certainly is correct; see Lagrangian point#Stability. –EdC 23:17, 30 January 2007 (UTC)

What is M? It suddenly apears in the L2 description. --5telios 12:38, 25 April 2007 (UTC)

Lagrangian points and spacecraft

The article speaks of multiple existing and planned spacecraft operating at a single Lagrangian point. Of course, it's impossible for multiple objects to occupy the same point in space, so I'm assuming that the spacecraft are/will be within a certain radius that's "close enough". Could some text be added to explain this?--Nonpareility 22:43, 30 January 2007 (UTC)

Again, Lagrangian point#Stability explains how quasi-stable, quasi-periodic orbits around the L-points can exist. Where relevant, "at" should be amended to "in orbit around". –EdC 23:19, 30 January 2007 (UTC)

Science Fiction Counter-Earth Lagrangian?

Is a science fiction "counter-Earth" actually a Lagrangian concept when it's not an object of "negligible" mass -- and the two Earths would seem to be just counter-balancing each other? (Well I mean "Earth's Evil Twin" -- same mass.)

Asteroid(s) orbiting Earth at L4/5?

Wasn't there a discovery in the last few years of one or two asteroids at/orbiting the Earth-Sun L4 and/or L5 points? —The preceding unsigned comment was added by 67.121.242.84 (talk) 23:53, 30 January 2007 (UTC).

Exact position of L4 and L5, plus minor amendment to figure

In subsection L4 and L5 :

Para 1 has "The L4 and L5 points lie at the third point of an equilateral triangle whose base is the line " no, "The L4 and L5 points lie at the third corners of two equilateral triangles whose common base is the line " or " ... whose bases are ...".

Well, it could be "The L4 and L5 points each lie at the third point...". Your wording is better, though. EdC 17:39, 23 February 2007 (UTC)

Para 1 has "whose base is the line between the two masses" - suggest '... between the centres of the two ...'. That does not change the natural meaning, but it does stress 'centres'.

Yes. EdC 17:39, 23 February 2007 (UTC)

Para 1 has "the smaller mass in its orbit around the larger mass". But both masses orbit the barycentre, and L4/L5 are outside the orbit of the secondary. Omit "in ... mass"?

I don't think "in its orbit" is intended to convey that they share the orbit; rather it is intended to qualify "ahead"/"behind". It could be misleading, though; I've changed "in" to "with regard to". EdC 17:39, 23 February 2007 (UTC)

Result could be "The L4 and L5 points lie at the third corners of two equilateral triangles whose common base is the line between the centres of the two masses, such that the point is ahead of (L4), or behind (L5), the smaller mass."

Changed, modulo the above. EdC 17:39, 23 February 2007 (UTC)

By the way, L4 is ahead of the secondary but behind the primary, in angle frem the barycentre. If mass were steadily transferred from primary to secondary, then as the secondary became the primary and vice versa, so would L4 and L5 exchange names.

True, but rather irrelevant, as L4 and L5 are only stable when there is a large disparity in mass between primary and secondary; binary star systems don't have trojan points. EdC 17:39, 23 February 2007 (UTC)

Well, we're dealing with Lagrange points, not Trojans. Pluto-Chiron, mass ratio about 10, still has five L-points but no T-points. The property is necessary for an exact solution. It should have a place in more mathematical pages.

82.163.24.100 22:41, 26 February 2007 (UTC)

Last para ends ", and asteroids there are named after characters from the respective sides of the war". Nowadays they are; but the convention was not established in the early days. See entries for 'Trojan asteroid', 'Trojan camp', 'Greek camp'. Given the detail elsewhere, I think the quoted bit can be omitted, or replaced by something like "; but there is a spy in each camp".

A little too humourous for an encyclopaedia, I think. A "mostly" qualifier will suffice; the reader can anyway follow the links to the detail, as you point out. EdC 17:39, 23 February 2007 (UTC)

In subsubsection Examples the page has "The Sun–Earth L4 and L5 points lie 60° ahead of and 60° behind the Earth in its orbit around the Sun." No, just outside its orbit. Maybe better to put it from another aspect - something like "As measured from the centre of the Sun, L4 and L5 are 60° ahead of and behind the Moon in the line of its orbit."

Again, I think "in its orbit" has a different intended meaning from how you're reading it. I've changed "in its orbit around the Sun" to "as it orbits the Sun". EdC 17:39, 23 February 2007 (UTC)

Figure

If the top-of-page diagram can again be edited, I suggest moving the blue triangles at L3 outwards a modicum, so that the grey circle of the Earth's orbit can be seen as it passes L3.

82.163.24.100 12:11, 23 February 2007 (UTC)

Doable, yes; unfortunately every time that image gets edited it loses quality (it's in JPEG). I'd prefer to develop Image:Lagrange points.svg to the degree that it can replace the NASA image.

By the way, Wikipedia is the encyclopedia that anyone can edit; your suggested edits would have been fine had you made them yourself. Be bold, I think the saying is. EdC 17:39, 23 February 2007 (UTC)

(1) not until I'm more familiar with page-editing convention, (2) A second opinion is valuable.

82.163.24.100 22:41, 26 February 2007 (UTC)

Correction to first diagram?

Shouldn't the L4/L5 arrows in the first diagram face inward and be red?--Michalchik 00:51, 10 March 2007 (UTC)Michalchik

Nope. Sorry. AFAIK the diagram is correct. I never did get my head around why it's the other way than you would expect, but I think it's something to do with coriolis effects closing the orbit.WolfKeeper 08:30, 10 March 2007 (UTC)

Euler and collinear libration points

In a lecture at CalTech in 2004, Shane Ross asserted that Euler first "discovered" the collinear libration points in the 3-body problem. Is there any written source to cite for this? Sdsds 21:39, 25 March 2007 (UTC)

L1 intuitively (mis) understood

The article currently makes the assertion regarding L1: "It is the most intuitively understood of the Lagrangian points: the one where the gravitational attractions of the two other objects effectively cancel each other out." Is this a good first-order understanding of stability at L1? It seems to work like that when viewed in a rotating frame of reference. But isn't a rotating frame of reference non-inertial? Aren't there are psuedo-forces that need to be considered? Considering L1 in a non-rotating frame centered at the barycenter of the system, would one in general expect the period of rotation of an object at the L1 point to match the period of rotation of of the smaller mass? Wouldn't it move out of alignment? What's really "intuitive" in the L1 case? Sdsds 22:19, 11 April 2007 (UTC)

Hmm, these are good questions. Basically, the L1 point is the only one that you expect to see in a non-rotating reference frame. i.e., if just had two solid masses sitting still, you would expect to find an equilibrium between them. Of course, this equilibrium is not at the same place as you find L1, due to the centrifugal 'force' you mention. So maybe this isn't really all that intuitive. Grokmoo 15:18, 13 April 2007 (UTC)

If you just had two solid masses sitting still, you would expect gravity to draw them together! What you describe would only make sense if you somehow pinned the locations of those two masses. In that totally weird and uncreatable situation, then it would be possible to "balance" a third object at a point somewhere near L1. But this is a fundamentally flawed approximation of the true situation: there are "obviously" no orbits around that balance point as there are around L1. Sdsds 14:30, 25 April 2007 (UTC)

OK, maybe after all it really is as simple and intuitive as it seems! (Sdsds - Talk) 16:59, 6 May 2007 (UTC)

A contour plot of the effective potential (the Hill's Surfaces) of a two-body system (the Sun and Earth here), showing the five Lagrange points.

Diagram caption

This currently says,

"... The blue arrows indicate the boundaries of the stable areas, beyond which an object would fall away from a Lagrange point; the red arrows indicate the planes along which an object will fall back towards a Lagrange point."

No they don't. The blue arrows around L4/5 aren't at the largest orbits, and there are no stable areas around L1/2/3. The red arrows don't indicate planes; they indicate directions within the orbital plane. What the arrows actually indicate is the slope of the pseudopotential surface: downhill away from local highpoints L4/5 (blue), downhill from the saddlepoints L1/2/3 along the line connecting the masses (blue), and downhill toward the saddlepoints in the perpendicular direction (red).
—wwoods 02:08, 24 May 2007 (UTC)

Mass of Lagrangian object?

What is the maximum mass, relative to the two main bodies, that an object in a Lagrangian point can have? For example, how large could an object be in the Sun-Earth L4 or L5 point? Nik42 01:35, 26 May 2007 (UTC)

Gundam Wing

Each of the pilots comes from a different lagrange point. Heero from L1, Duo from L2, and so on. It's where they get the numbers that the characters are originally reffered to by the Order of the Zodiak before they obtain their names. It's also that same practice used in fanfiction when reffering to relationships. NemFX 00:53, 4 June 2007 (UTC)

Footnote 3

Footnote 3, referring to the "24.96" which is the minimum ratio between M1 and M2 to have stable L4 and L5 points, says:

Actually $\left(25\left({\frac {1-{\sqrt {1-4/625}}}{2}}\right)\right)^{-1}$

Isn't that rather a complicated formula which can be expressed more simply? If I've done my math right,

$\left(25\left({\frac {1-{\sqrt {1-4/625}}}{2}}\right)\right)^{-1}={\frac {25+3{\sqrt {69}}}{2}}$

and the latter is not only a simpler, but also a more conventional way to express the number. Would someone double-check my math and verify that? Chuck 23:04, 11 June 2007 (UTC)

Yes, you're right. I've changed the article to use the simpler expression. --Zundark 10:09, 12 June 2007 (UTC)

merge with L1 orbit

I cant see any reason there should be a second page for L1 orbit. Chris H 13:12, 29 July 2007 (UTC)

Support. I have reworked the merge suggestion tags to indicate where discussion of L1 fits into this article. (And this article is not yet too long to include what's in the L1 Orbit article! ;-) (sdsds - talk) 21:56, 29 July 2007 (UTC)

/History and Concepts/

"In 1772, the Italian-French mathematician Joseph-Louis Lagrange was working on the famous three-body problem when he discovered an interesting quirk in the results."

What quirk is that exactly? I don't know, although I'd presume it's the hypothesis referred to later. In any case, it's unclear. Can someone look at this? --60.230.200.219 11:19, 23 September 2007 (UTC)

Source of L4/L5 claim

The section on natural objects claims bodies in Sun/Saturn and Jupiter/Jovian satellite Lagrange points. AFAICT, there's no other mention of such things elsewhere in Wikipedia, and no source cited here. Do they really exist? ~Lynn M —Preceding unsigned comment added by 131.212.212.174 (talk) 18:50, 26 September 2007 (UTC)

Pop culture

Pop culture list is long and detracts from the main article. Should be moved to a seperate article list of lagrangian points in fiction or so. For now, marking it as trivia, for want of a better tag. Brianski 04:37, 30 October 2007 (UTC)

Other Co-orbitals

Technical point behind edit. The higher, slower orbit represents a greater orbital energy rather than lower. Wording adjusted to reflect that. roger.ritenour, 28 November 2007 —Preceding unsigned comment added by Roger.ritenour (talk • contribs) 14:56, 28 November 2007 (UTC)

PS - See Wikipedia:What_Wikipedia_is_not

Pitch Black scenario

The Pitch Black (film) article does not currently address the use of Lagrange points in the movie. To tell you the truth, I don't know how much they've been discussed at all, but the movie clearly shows a scenario with a planet at the middle of an orrery with a star and a double star revolving on opposite sides, which presumably makes it an L1 point. To add to the complexity a pair of gas giant planets orbit the L1 point (with different periods, I think). The question is... is it conceivably possible? I know the L1 point normally would be an unstable spot for a planet, but I won't even pretend I know what happens to a five body system. 70.15.116.59 (talk) 02:08, 31 December 2007 (UTC)

Proposal to add section "Proposed objects"

It might worth noting somewhere the proposals (Space sunshade and Solar shade) to place a large "sunshade" at the L1 point to counteract the effects of global warming. (Give these proposals some though before dismissing them out-of-hand.) There are sections for existing and fictional objects at the Lx points, but there is no section for proposed objects. 220.76.15.253 (talk) 18:12, 27 October 2008 (UTC)

Earth-Moon L2 Point

The article doesn't mention go into detail on the Lagrangian point on the other side of the moon; for example this orbit is an option for Constellation Program Moon relay satellites. MithrasPriest (talk) 18:46, 5 November 2008 (UTC)

Rubber sheet analogy

If the contour map were replaced with a rubber-sheet visualization (i.e., the kind that are popular for depicting gravitational distortions of space-time), would it be accurate to say that the L-points are the highest points on the ridges between the astronomical bodies? If that's the case, it would be fairly obvious that these locations are not stable, and that if an obejct at such a point is nudged away from that point, it will "fall into" the gravity well of one of the bodies, right? | Loadmaster (talk) 17:43, 3 December 2008 (UTC)

L-4 and L-5 are the highest points of the pseudopotential, yes. Picture a volcano, with a deep central crater, and a smaller crater breaking its rim.

If an object is released near one of those points, it falls away from them, but the Coriolis force pushes it sideways, driving it along the contour lines which are closed around the points, so it never leaves the vicinity.

By contrast, L-1, -2, and -3 are saddle points. An object released there can wander about the system

—WWoods (talk) 20:24, 3 December 2008 (UTC)

Rocheworld

Surely the Rocheworld waterfall is at L1, not L4?

Comsats were placed at L4 and L5.

82.163.24.100 (talk) 20:09, 4 May 2009 (UTC)

Indeed. —Tamfang (talk) 06:34, 11 May 2009 (UTC)

L2 is relatively close to the Earth

The first diagram claims to be "A contour plot of the effective potential of a two-body system (the Sun and Earth here) ..." Isn't that misleading? The radius of the Earth's orbit is 150 million km, and the distance from the Earth to L2 is 1.5 million km, so L2 is really snugged up close to the Earth. I see that a contour plot on that scale would be too difficult to read, but I think the caption should be changed to make the relationships clear, or at least not misleading. Maybe making the plot for the Earth and the Moon would help, since their masses are more nearly comparable. --Art Carlson (talk) 08:34, 19 May 2009 (UTC)

...likewise L1. —Tamfang (talk) 19:48, 19 May 2009 (UTC)

Right. I'm fixating on the Planck satellite. I'm pretty sure the islands around L4 and L5 will shrink down to specks as well. --Art Carlson (talk) 20:40, 19 May 2009 (UTC)

L2 and Umbra

For circular orbits and a relatively light secondary, it is sufficiently easy to show that L2 is within the umbra if the secondary is less than three times denser than the primary. The density ratio for L2 being at the umbra tip is quite sensitive to the mass ratio. See in http://www.merlyn.demon.co.uk/gravity4.htm. At present, the Article says little about that. 82.163.24.100 (talk) 15:21, 16 September 2009 (UTC)

Execrable Prose Style!

Regardless of technical content, the prose style of this article is uniquely bad among WP science articles, which as a group are the worst content on WP. This is a real shame and a true mystery. Something should be done to organize the WP science pages and ruthlessly weed out this awful writing. Antimatter33 (talk) 15:19, 9 December 2009 (UTC)

The High Frontier

The first reference to "The High Frontier" by Dr. Gerard K. O'Neill should not be within a section headed "In fiction". 82.163.24.100 (talk) 20:25, 2 February 2010 (UTC)

Introduction

It seems to me that the sentence "The Lagrange points mark positions where the combined gravitational pull of the two large masses provides precisely the centripetal force required to rotate with them." should be improved by inserting "for the object" between "required" and "to". If you agree - do it! And "pull" should be "pulls"? 82.163.24.100 (talk) 13:00, 28 October 2010 (UTC)

External Links

http://www.merlyn.demon.co.uk/gravity5.htm shows Lagrange points moving under various conditions; it might be worth adding, but it is linked from gravity4.htm (the old g5 is now g6). 94.30.84.71 (talk) 21:23, 8 February 2011 (UTC)

Add M1 M2 to diagram

The article discussed M1 M2 etc., but these symbols do not appear in the diagram. One would have to read the whole article to discover the definition of M1 and M2. This is quite frustrating. —Preceding unsigned comment added by 75.53.54.121 (talk) 18:32, 28 February 2011 (UTC)

History and concepts

In the final paragraph of the section, the word "area" appears inappropriate. It seems to me that, in rotating co-ordinates, the system of two bodies and five points maintains a constant shape, varying in size. Then, at any instant, each L-point has a point location, which moves in and out in rotating co-ordinates and on an elliptical track in fixed co-ordinates. 82.163.24.100 (talk) 16:40, 23 June 2008 (UTC)

http://www.merlyn.demon.co.uk/gravity5.htm can now show the Lagrange points for elliptical orbits as seen by a co-rotating observer, who sees that each of the five points moves in a straight line. The observer's angular velocity is of course not constant. The path traced out by the points, in these coordinates, does not enclose an area. 94.30.84.71 (talk) 22:37, 12 June 2011 (UTC)

Trojans

In a general article on Lagrangian points, the string "Trojan" ought to appear at least once. 94.30.84.71 (talk) 22:03, 15 June 2011 (UTC)

I count sixteen. Is that excessive? —Tamfang (talk) 03:40, 16 June 2011 (UTC)

Oops. No. Perhaps I used a case-sensitive search. I understand that there is one Greek in the Trojan camp, and vice versa. 94.30.84.71 (talk) 22:25, 26 June 2011 (UTC)

Yes, named before the convention caught on. —Tamfang (talk) 00:12, 29 June 2011 (UTC)

ESA explanation

I found this article today on L points at the ESA website: http://www.esa.int/esaSC/SEMM17XJD1E_index_0.html. The animations are very easy to understand, as are the explanations. Maybe it's just me, but I found this much easier to follow than the "stone at the end of a string" examples in the 'Intuitive explanation' section. I'm wondering if ESA material is PD and could be incorporated into the article somehow. —divus 05:55, 6 July 2009 (UTC)

As of yesterday, the ESA material, while generally good, did not appear completely accurate. 94.30.84.71 (talk) 10:33, 24 July 2011 (UTC)

Image is wrong.

I'm sorry. I don't speaking english. TT I Want you to understand it.

Arrow around L4 and L5 in Vector Image (http://en.wikipedia.org/wiki/File:Lagrange_points2.svg) is wrong. The surrounding arrow is to make the opposite direction because of L4 and L5 is a stable equilibrium point. --Goldenbug (talk) 19:58, 12 July 2011 (UTC)

Yes it is wrong and generally chaotic. It needs (at the very least) the following fixes:

• the L4 and L5 surrounding arrows each needs a 180° turnaround, and being colored red,
• the gravity well indicating curves should all be removed, they make a visual chaos — instead I propose indicating the gravity well with gray shades, f.ex. gray deep in the well and white in gravity-zero-space,
• the direction of earth's orbit movement needs a clearly visible arrow,
• earth is almost invisible against the background, when choosing an appropriate background color for the gravity well, earth needs a strongly contrasting color,
• the figure should be adapted to low sizes, the letters already are big – good! – earth and the lagrange points need to be big,
• the lagrange points themselves should need a large clearly visible symbol that is not round or any conventional astronomical symbol (stars, planetary nebulae or such), f.ex. haircrosses or squares (maybe)

First fixer gets all the glory! Rursus dixit. (^mbork³!) 07:50, 30 July 2011 (UTC)

/harrumph/! Diging into the topic, I'm a little unsure what the "arrows" (red and green blue triangles) represent. It might be that the blue arrow pointing away from the L-point might instead be an uphill mark as used in geographic maps. Very misleading indeed. Maybe they should be replaced with arrows pointing "downhill" to indicate movement tendencies? Rursus dixit. (^mbork³!) 08:11, 30 July 2011 (UTC)

No the arrows all point downhill. In the pseudopotential, L-1, -2, and -3 are saddle points, while L-4 and -5 are the highest points. I've tried to clarify this in the caption.

—WWoods (talk) 19:17, 30 July 2011 (UTC)

External Links

I have added to the Article two links to images of Lagrange's "Essai sur le Problème des Trois Corps". That is something which anyone considering contributing to the Article ought to have read. 94.30.84.71 (talk) 10:31, 24 July 2011 (UTC)

For the benefit of those unfortunates who cannot understand French as PDF images, I am about to add a link to a translation into English as HTML of the words of the "Essai". For the best experience, have JavaScript enabled, and a copy of the original also open to show the equations. 94.30.84.71 (talk) 19:17, 15 August 2011 (UTC)

Since Cain and Gay wrote that gravity cancels out at the L-points, I suggest that their link should be removed. 94.30.84.71 (talk) 17:30, 24 July 2011 (UTC)

References

Reference 6 may be dead. 82.163.24.100 (talk) 14:02, 13 April 2009 (UTC) Now http://wmap.gsfc.nasa.gov/media/ContentMedia/lagrange.pdf 82.163.24.100 (talk) 15:18, 13 April 2009 (UTC)

Current Reference 3 is at present a 404. Also (1867–92) are highly unlikely dates for Lagrange, which is what they look like there. They are probably the dates of the 'Oeuvres'. The Reference should be removed; the link to ULg serves. 94.30.84.71 (talk) 20:14, 15 August 2011 (UTC)

Geostationary analogy

"They are analogous to geostationary orbits in that they allow an object to be in a fixed position relative to one or two bodies rather than any more general orbit in which its relative position changes continuously."

This geostationary analogy is not at all compelling and will only confuse anyone who does not already understand what a Lagrange point is. It should be removed rather than re-worked but I suspect that if I just remove it someone will revert the edit.154.5.32.134 (talk) 04:52, 28 July 2011 (UTC)

Agreed. I commented it out. 94.30.84.71 (talk) 20:25, 15 August 2011 (UTC)

General Review

The Situation

There are two main problems with the Article as it stands today.

(1) Contributors have not read, or have not understood, Chapters I & II of Lagrange's Essai of 1772 (I'm assuming that to be his only relevant publication; I've read the rest of the Essai and all the Subject entries of the Oeuvres).

(2) Contributors, some of inadequate understanding, have shovelled in anything they can think of that is vaguely related. An encyclopaedia article should concentrate on its subject, and should link to other articles rather than include what should be their content.

94.30.84.71 (talk) 22:15, 15 August 2011 (UTC)

Introduction

It describes the common view. But Lagrange was trying to solve the general three-body problem, and, from the equations he derived, he proved that there are two types of exact solution in which the pattern of the bodies, without regard to scale, are preserved. One type was known to Euler (L1 L2 L3), the second was found by Lagrange (L4 L5). Lagrange paid no particular attention to circular orbits or even to whether the system was rotating - the paths of the bodies are, he found, conic sections.

Replace, above, "One type was known to Euler (L1 L2 L3)" with "A non-rotating collinear constant-pattern solution was found by Euler. 94.30.84.71 (talk) 11:21, 27 August 2011 (UTC)

I've now examined the Euler Archive site. Judging by the titles, only E.327, E.400, and E.626 can be relevant. All deal only with motion in a straight line, without any rotation. That cannot be said to amount to a prediction of L1 L2 L3 as commonly known. 94.30.84.71 (talk) 17:20, 21 August 2011 (UTC)

Using Lagrange's approach, but with virtually no equations, it is easy to show (easier than in the present Article) that the equilateral pattern, with the three massive bodies initially given a symmetrical pattern of velocities, is persistent. One can see that, for some spacing, any three bodies in a line must also be capable of persistence.

Previous sentence "One can see" - indeed, one can easily prove it, and solve for the spacing, by following Lagrange's approach. 94.30.84.71 (talk) 11:16, 27 August 2011 (UTC)

History and concepts

A reference to Euler's relevant work is needed (i.e. to Euler's own writing).

The present Reference 2, Koon et al, is unsatisfactory as it does not load, perhaps being too big. It needs to be replaced or supplemented by something else providing information on Euler's contribution. 94.30.84.71 (talk) 19:45, 16 August 2011 (UTC)

I have succeeded in fetching it. The relevant part is wrong, so there should be no Reference for Euler. 94.30.84.71 (talk) 11:25, 27 August 2011 (UTC)

I do not think that, in the Essai, Lagrange used 'action' as described.

I've looked again, and he did not. 94.30.84.71 (talk) 19:45, 16 August 2011 (UTC)

He did not use negligible mass or circular orbit.

The 'host bodies' cannot both be planets, though one of them usually is.

The Lagrangian points

The caption should include the word "circular". It would be better to use the Earth-Moon system, since for that L1 & L2 are more separated from the secondary and can be marked more clearly.

L1

"It is the only L-point which exists in non-rotating systems." Remove, as incorrect.

The idea is that if there are two stationary masses, there's a point between them where their gravitational forces are equal-and-opposite; this corresponds to L1. There's nothing like the other four, without the centrifugal force for balance.

—WWoods (talk) 20:38, 16 August 2011 (UTC)

"In a binary system," - phrase not needed. For a system of two massive bodies, whatever they may be, the Roche lobe apex is at L1.

L2

Unnecessary art; the previous diagram suffices.

The diagram may have been taken from ESA's Lagrange Point page - permission? 94.30.84.71 (talk) 19:27, 16 August 2011 (UTC)

"beyond the smaller of the two" - should be "beyond the lighter of the two". Size is not important.

L4 and L5

A better argument, valid for three massive objects independently of the shape of the orbit, exists.

Intuitive Explanation

"Lagrangian points L2 through L5 only exist in rotating systems," - incorrect. Well, a bit of a moot point! The entire raison d'etre of Lagrangian points is in a rotating 3-body system !

"Imagine a person spinning a stone ...". Inappropriate. The place for that, if any, is in the Wikipedia articles on centrifugal/centripetal force.

"Unlike the other Lagrangian points, L1 would exist even in a non-rotating (static or inertial) system." - Balderdash. In Lagrange systems, the only true forces are the gravitational ones. If there is no rotation, the bodies/particles all fall into the barycentre, maintaining their pattern (what happens when they get there is not germane). Of there is infinitesimal rotation, the bodies will orbit perpetually in ellipses of infinitesimal but proportionate widths, swooping round the barycentre in a manner worse than in Niven's "Neutron Star".

The rest of the section would, if correct, be superfluous. This : "or spirals in toward the barycenter" illustrates the shallownwss of its author's understanding

Lagrangian point missions

That material would be better placed elsewhere, in "List of objects at Lagrangian points" or in a new similar article.

Natural examples

Likewise. There are enough examples above; the Article should be about theory illustrated by sufficient examples, no more.

Other co-orbitals

2010 TK7 is "at" S-E L4. It should not be further described here; it has its own article.

Cruithne, Epimetheus, Janus are not Lagrangians. They deserve, if that, no more than a mention to plant a link.

94.30.84.71 (talk) 22:15, 15 August 2011 (UTC)

Additions needed?

The article should, I think, say a little more about the size and shape of the useful volumes aroundd L1 L2 L3, and of the size and shape of the regions in which particles bound to L4/L5 may be found. If the primary/secondary separation is taken as 1, and the orbits as near-circular. the only relevant variable will be the mass ratio.

Stability : I assert that the triangular configuration is stable for two bodies and a particle in circular orbit if the mass ratio secondary/primary is smaller than a number about 0.04 which can be calculated exactly. I think that if the primary mass is 1, the system is stable if the sum of the other two masses is less than about 0.04, with very little dependence on the ratio of the smaller masses. That needs independent proof.

Article should include something about "Stable if   27(m1m2 + m2m3 + m3m1) < (m1 + m2 + m3)^2". That derives from Routh's Criterion, but I don't have any really good reference to offer for that expression. 94.30.84.71 (talk) 19:37, 16 August 2011 (UTC)

That's enough for tonight. 94.30.84.71 (talk) 22:15, 15 August 2011 (UTC)

History and concepts

Paragraph 2, "in 1772, ..." : Is there evidence that Lagrange previously did significant work on the more-than-three body problem? If so, a link of some sort is needed; otherwise, there is no need for the second sentence, "Originally ... achieved.". 94.30.84.71 (talk) 17:19, 2 May 2012 (UTC)

Paragraph 3, "The logic ... trajectory.". seems superfluous. 94.30.84.71 (talk) 17:19, 2 May 2012 (UTC)

Paragraph 4, "Lagrange, however, ... in 1906." : Is it clear that, for this work, Lagrange used "action"? I have not recognised it in the Essai. In the Essai, I see nothing about "negligible mass" or "near-circular orbit" or rotating frames of reference. A body in a curved path CANNOT be experiencing zero ner force; centrifugal force is fictitions and superfluous. Only L4 L5 "follow" the orbit of another body, and they do not do that exactly. I think that the author of this section has regurgitated material from a second-rate textbook or lecture course. 94.30.84.71 (talk) 17:19, 2 May 2012 (UTC)

Error in Introduction

The Introduction has "Lagrangian points are the stationary solutions of the circular restricted three-body problem.". That is an impractical definition, since no planet or satellite orbits in a circle. It would, though, be OK to have "The stationary solutions of the circular restricted three-body problem are called Lagrangian points." - although that does not say anything about real off-circular Lagrange Points. 94.30.84.71 (talk) 17:41, 9 May 2012 (UTC)

Formal Definition

Is there a formal definition of Lagrange and/or Lagrangian Point - one with real authority, not a dictionary or a personal opinion? If so, the Article should use and cite it. If not, then there should be. Any definition needs to be entirely compatible with what Lagrange actually wrote (by the way, did he publish anything relevant other than the Essai?). It should also be fully compatible with current usage, but might be broader. 94.30.84.71 (talk) 22:02, 9 May 2012 (UTC)

The Lagrange Points are the relative positions of the lightest body, when of negligible mass, in constant-pattern solutions of the three-body problem. ?? 94.30.84.71 (talk) 18:54, 12 May 2012 (UTC)

New Section for Article : General Explanation

This is a draft new section, which will enable the removal of almost all of the existing Intuitive explanation section. If any of the styling needs fixing, please fix it in situ, if you can. After a few days, I'll move the new section over. 94.30.84.71 (talk) 18:42, 8 May 2012 (UTC)

Bodies Moving in Constant Patterns

The "pattern" of a set of bodies depends only on the angles between them, and does not depend on position, orientation, and scale. The pattern of a set of massive bodies affected only by their mutual inverse-square gravitation may remain constant. Such a pattern may or may not be stable against small perturbations.

The relative acceleration of any two parts of such a constant pattern must be in constant proportion to the inverse square of the current size of the pattern. The barycentre ("centre of gravity"), which does not accelerate, can be considered as a part of the pattern. The total angular momentum about the barycentre is constant, and must be divided in a constant fashion among the bodies. So the angular momentum of each body around the barycentre is constant, and the net field at each body must be (bary-)central.

Newton has shown that the path of a body subject only to a central inverse-square net force is a conic section (circle, ellipse, parabola, hyperbola, straight line). Any conic section is a possible path for a body in a constant pattern, and laws similar to Kepler's will apply.

The Lagrange Points

Three bodies can remain in a constant pattern in two ways, with no more than the position, the size and the absolute orientation of the pattern varying with time, as shown below.

Euler's Work

Euler and Lagrange shared a Prize for general Moon theory. Euler (E.304) worked in Sun-Moon-Earth theory, but got no nearer to the Lagrange Points than solving the case of three bodies moving in a fixed straight line (E.327).

P.S. The Euler Archive is at http://www.math.dartmouth.edu/~euler/ . 94.30.84.71 (talk) 18:28, 16 May 2012 (UTC)

Lagrange's Work

Lagrange, in the Essai sur le Probléme des Trois Corps, attempted the general three-body problem. He concentrated extensively on the behaviour of the distances between the three bodies, rather than on their positions. Using his general equations, he found that there are two types of constant-pattern solution, one with the bodies all collinear and one with them all equidistant. The first gives what are now known as L1, L2 and L3, the second L4 and L5. He did not consider the stability of the patterns.

The Direct Approach

Dr J R Stockton, by following Lagrange in using the distances between the bodies, has proved the constant-pattern solutions directly, without considering the general three-body problem.

A Direct Proof for L4 and L5

An equilateral triangle ABC with opposite sides a b c remains equilateral if the variable rates of change of the lengths of its sides (db/dt, etc.) are always equal. If those rates are initially equal, they remain equal if their own variable rates of change (d²b/dt², etc.) are always equal.

For massive bodies A B C at the corners of an equilateral triangle currently of side s, the gravitational field component at A along side b is G(C+B/2)/s². So at any instant d²b/dt² is G(A+B+C)/s², etc., therefore d²a/dt² = d²b/dt² = d²c/dt², so the triangle remains equilateral.

Note : that applies for any three massive bodies, regardless of the shape of their paths, and does not use the inverse square law.

A Direct Proof for L1, L2 and L3

Let massive bodies A B C be initially in a straight line. Motion of their barycentre can be disregarded. Let their initial velocities be mutually parallel and in signed proportion to their distances from the barycentre. The bodies will initially remain collinear, and the ratios of their mutual distances will initially remain the same. The pattern will initially be constant.

If AB is infinitesimal, and BC is not, the accelerations will be such that AB/BC will clearly reduce; and vice versa. There will be an intermediate initial ratio AB/BC for which AB/BC remains constant. All of the initial conditions then still hold, and the pattern is preserved for ever.

The traditional Lagrange Points L1, L2, L3 correspond to setting the masses of the bodies A B C to represent in any order a primary body, a secondary body, and a particle.

For the velocities to remain proportional to the distances from the special point the accelerations, and hence the fields, must be similarly proportional. For that, one must construct the necessary equations (which reduce to a single quintic equation) and solve them. That is done in detail in section "Collinear Pattern - L1 L2 L3" at Simplified Lagrange Point Theory, which includes the algebra for the quintic equation and a Form for the iterative solution of the equations.

Note : that applies for any three massive bodies, regardless of the shape of their paths.

Further Work

For more detail and further work, see Simplified Lagrange Point Theory.

References

• Introductory : Gravity 4 : The Lagrange Points
• External reference lists are at :-
  • Gravity 4 : The Lagrange Points
  • Simplified Lagrange Point Theory

Comment

Here. 94.30.84.71 (talk) 18:42, 8 May 2012 (UTC)

History and concepts

I have rectified section "History and concepts" to agree with what Euler and Lagrange actually wrote, using the translations at the Merlyn site and directly reading other Euler papers. I have for the moment retained some parts which are apparently unnecessary but are not known by me to be actually false, adding HTML comment at the end of each. 94.30.84.71 (talk) 12:08, 4 July 2012 (UTC)

Query : Are there any other writings of Lagrange relevant to the topic - I have found none. 94.30.84.71 (talk) 12:08, 4 July 2012 (UTC)

Introduction

I have removed the inappropriate presumption of circularity from the Introduction. There are in practice no truly circular orbits, and Lagrange's work applies (exactly) to constant-pattern paths of any conic section, as his readers will see. 94.30.84.71 (talk) 13:14, 4 July 2012 (UTC)

limiting mass

I assume that there is a limiting mass for the body placed at the L point to have a stable orbit. That would be relevant for the destabilization of Theia. Anyone know? kwami (talk) 13:34, 3 May 2009 (UTC)

See page 2 top of http://www.lesia.obspm.fr/perso/bruno-sicardy/biblio/biblio/Sicardy_Gascheau_CelMec10.pdf - Gascheau was the first to study the stability of the L4 and L5 points (1843), showing that the motion of three non-zero masses m1,m2 and m3 in a rotating equilateral configuration becomes linearly unstable if (m1 + m2 + m3)² / (m1 · m2 + m1 · m3 + m2 · m3) ≤ 27. That condition is approximately equal to (m2 + m3)/m1 < 0.04, as illustrated in http://www.merlyn.demon.co.uk/gravity4.htm . 94.30.84.71 (talk) 16:26, 13 May 2012 (UTC)

Thanks! (Should that be a ">"? Negligible m2 and m3 should be stable.)

Since (m2 + m3)/m1 could never be > 0.04 (as m2 = 0.003 and m3 is less than that), it would seem that this cannot explain the destabilization of Theia.

The solution may be that it wasn't a 3-body problem. (See Giant impact hypothesis#Possible origin of Theia.)

— kwami (talk) 12:36, 17 October 2012 (UTC)

Euler link change

In External Links, I have changed the Euler link from the E.327 PDF at Dartmouth to the E.304 information page at MAA. The reasons will be obvious to those who have read the Euler Archives. 94.30.84.71 (talk) 22:38, 23 October 2012 (UTC)

Moreover, the present Reference 3 is to E.327, which discusses motion along a FIXED straight line, and so cannot be said to contain a discovery of the any Lagrange Points, since the Points are commonly considered to have near-circular paths. 94.30.84.71 (talk) 20:59, 24 October 2012 (UTC)

In E.304, now cited, Euler discovered L1 and L2 (by the rather drastic step of moving the Moon there), but did not discover L3 (a step too far? - but would have been compatible with his general reasoning). Nothing else by Euler appears to have revealed L3. The academics responsible for Reference 2 appear to have relied on rumour, without checking their facts, and should not be quoted on this matter. 94.30.84.71 (talk) 20:59, 24 October 2012 (UTC)

Circular and Restricted

The Lagrange Points are sometimes described as solutions of the circular restricted three-body problem. That is bad practice. Lagrange found the two constant-pattern configurations for the general three-body problem, and the merlyn site shows how easily those solutions can be verified if one avoids any attempt to solve for arbitrary initial conditions. The forms of the paths are in neither case artificially constrained; the solutions allow ANY conic section. Moreover, it is generally agreed that Lagrange Points exist in the Solar System, but every planet and moon has an elliptical orbit. 94.30.84.71 (talk) 21:16, 24 October 2012 (UTC)

Although the calculations allow all conic sections as paths, one might choose to use "Lagrange Points" only for the near-circular solutions. That seems ungenerous to Lagrange. 94.30.84.71 (talk) 21:16, 24 October 2012 (UTC)

External Link to be Removed

The External Link to "The Five Points of Lagrange" by Neil deGrasse Tyson needs to be removed, as it has historical and technical errors, and adds nothing that is needed. 94.30.84.71 (talk) 12:52, 26 October 2012 (UTC)

That diagram

The five Lagrangian points (marked in green) at two objects orbiting each other. (Here a yellow sun and blue earth)

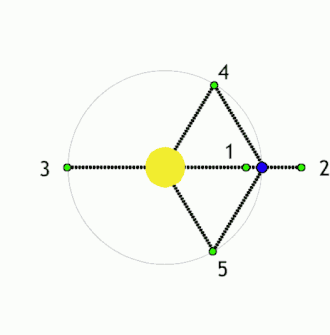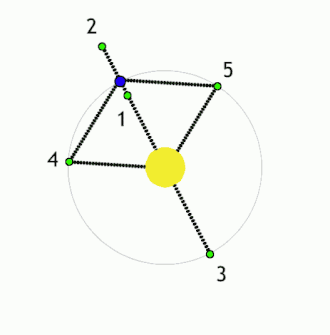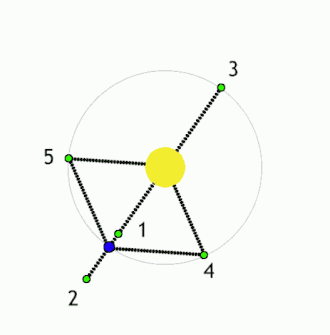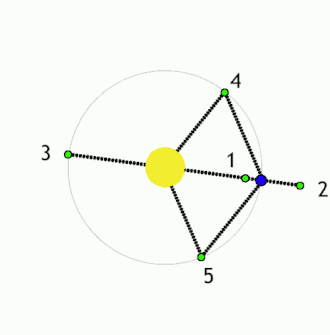
This diagram is seriously flawed. The distances from the Earth to Sun/Earth L1 & L2 are nearly equal, at 1.5 million km, ~1% of the Earth Sun distance. The L3 point is nearly the same distance from the Sun as L2, I believe, a little over 1 AU. Can someone who knows how to fix the .gif modify it? If not, I think it adds little and needs to be removed. Thanks. Wwheaton (talk) 19:50, 8 August 2010 (UTC)

L3 is more nearly the same distance from the primary as the secondary is. 94.30.84.71 (talk) 11:20, 9 February 2011 (UTC)

It is easy to take a copy of the GIF and edit it in Windows Paint. Uploading is another matter. 94.30.84.71 (talk) 11:58, 9 February 2011 (UTC)

Best replacement would be a new SVG modeled on the PDF at caltech.edu: "Dynamical Systems," etc. by Koon, Lo, Marsden and Ross, page 9. Rursus dixit. (^mbork³!) 08:35, 30 July 2011 (UTC)

In the Article, the second diagram (shown here; http://en.wikipedia.org/wiki/File:Lagrangianpointsanimated.gif) should be replaced by the third diagram, http://en.wikipedia.org/wiki/File:Lagrange_very_massive.svg. It would be well is someone who knows how would enlarge the text within the latter. 94.30.84.71 (talk) 17:51, 4 July 2012 (UTC)

Text enlarged... cmɢʟee୯ ͡° ̮د ͡° ੭ 19:26, 14 February 2013 (UTC)

Why 'Lagrangian point' instead of 'Lagrange point'?

I've studied physics for a long time, and I never heard the term 'Lagrangian point' until looking at this Wikipedia article. Everyone I know says 'Lagrange point'. 'Lagrangian' sounds stupid, because it means something else very different in classical mechanics. I get the feeling someone unfamiliar with this subject edited the title. I could be wrong, but.... John Baez (talk) 04:18, 11 March 2013 (UTC)

Lagrangian is simply the adjective (more famously used as a noun too of course), and some people prefer it. I think it could be good to pick one form and use it consistently throughout the article, while introducing both forms in the lede. Martijn Meijering (talk) 17:52, 11 March 2013 (UTC)

Lagrangian point missions

WMAP seems no longer operational. 94.30.84.71 (talk) 20:31, 20 May 2012 (UTC)

yes, fixed--agr (talk) 17:03, 18 March 2013 (UTC)

sonde at L4 and L5

The Japanese Sonde Hiten launched 1990 made swingbys at moon and visited Lagrangian points L4 and L5 to collect dust there. NASA. Retrieved 3.2.2010. —Preceding unsigned comment added by Helium4 (talk • contribs) 13:05, 3 February 2010 (UTC)

...shouldn't this be added under the missions section? 128.210.206.145 (talk) 08:38, 18 March 2013 (UTC)

Added--agr (talk) 17:16, 18 March 2013 (UTC)

L3 - further question

Under the L3 section it says - "the Sun–Jupiter system is unbalanced relative to Earth (that is, the Sun orbits the Sun–Jupiter center of mass...)". Should that not be "the Sun–Jupiter system is unbalanced relative to Earth (that is, the Earth orbits the Sun–Jupiter center of mass...)"? BigSteve (talk) 15:48, 28 February 2013 (UTC)

OK, I see no one wants to answer this one. How about this –

PLEASE someone explain HOW the Earth's gravity EQUALS the Sun's at L3...at a distance of 300 million kilometres...??? BigSteve (talk) 09:15, 23 March 2013 (UTC)

It doesn't, obviously. Where does the article say this? --JorisvS (talk) 11:42, 23 March 2013 (UTC)

Well, the fact that L3 is stable means that it is. For want of better scientific phraseology...how else do objects stay stuck there? BigSteve (talk) 13:57, 23 March 2013 (UTC)

No, it doesn't. The combined gravity of planet+Sun means that an object near the planet's L3, which is located slightly outside its orbit, can orbit there with the same (average) orbital period as that planet. --JorisvS (talk) 14:47, 23 March 2013 (UTC)

OK, but that still doesn't explain Why and How! :-) I get the complex mathematical formulas (well, actually, I don't, but I trust you that they are correct), but can someone please explain in the article for non-mathematicians how and why L3 exists... BigSteve (talk) 16:03, 23 March 2013 (UTC)

Well, it basically does. An object can orbit there with the same period as the planet. This is because the object at the L3 feels things like a slightly higher gravitational attraction coming from the Sun (which is because of the planet on the other side the Sun). This means that at a slightly greater semi-major axis it can orbit with the same orbital period as the planet. This is the reason that the L3 exists. The reason that it is stable is that when the object deviates from the L3, it effectively feels a small force directed towards the L3. --JorisvS (talk) 10:46, 24 March 2013 (UTC)

That's crazy... Could you add this explanation in the article? Perhaps adding a mention of what seems to me, looking at the contours, as if the Earth's gravity almost goes around the Sun...?! A bit like a magnetic field would. Which I guess also has something to do with it? BigSteve (talk) 11:01, 24 March 2013 (UTC)

Crazy? What do you mean? Gravity does not behave like magnetic fields. --JorisvS (talk) 11:58, 24 March 2013 (UTC)

The contours are that of the gravitational potential, not of the gravitational force. --JorisvS (talk) 12:01, 24 March 2013 (UTC)

"Crazy" in a positive way! As far as the gravity contours... File:Lagrange points2.svg – seems pretty magnetic-like to me, esp. the contours around L4 and L5, which seem to me to be definig the position and stability of L3...by going around the Sun. Unless I'm not understanding it? BigSteve (talk) 12:06, 24 March 2013 (UTC)

That's a gravitational-potential plot, which definitely does not behave like magnetic fields. Magnetic fields are vectors, whereas gravitational potentials are scalars. I don't know, however, what the blue and red triangles are supposed to mean. As the image description says, the lines in the picture are gravitational-potential contours and objects in free fall will trace out such a contour (or intermediate ones). --JorisvS (talk) 14:05, 24 March 2013 (UTC)

Hm... BigSteve (talk) 21:25, 24 March 2013 (UTC)

L4 and L5 on File:Lagrange very massive.svg

The caption for this image in the The Lagrangian points section reads "In such a system, L3–L5 will appear to share the secondary's orbit, although in fact they are situated slightly outside it" (emphasis mine) with the "although" clause in agreement with the later math analysis. However, the image has L4 and L5 on the circle even when enlarged to 2000px, whereas L3 is indeed very slightly outside. Since I assume we're trying to illustrate the qualitative ideas here (rather than an exact solution for a specific situation), L4 and L5 should also be seen that way. DMacks (talk) 17:33, 2 April 2013 (UTC)

More general than what?

A paragraph in "History and concepts" begins with "In the more general case of elliptical orbits, there are no longer stationary points ...."

More general than what? The previous paragraph discusses the general case and conic sections, and also constant pattern solutions. Perhaps the referent here is when one mass is negligible, where "positions" are discussed, not "points". Perhaps there was a mention of circular orbits which was deleted. In any case, it's not at all clear what changes the points into areas. This sentence needs to be revised to make sense.

Thanks Learjeff (talk) 19:12, 21 May 2013 (UTC)

Bad links

External link "Astronomy cast - Ep. 76: Lagrange Points Fraser Cain and Dr. Pamela Gay" seems unworthy of mention. 82.163.24.100 (talk) 18:40, 9 August 2009 (UTC)

Also, the fourth link in the References, to Gallica, does not now work. 82.163.24.100 (talk) 19:31, 9 August 2009 (UTC)

Should it be http://gallica.bnf.fr/ark:/12148/bpt6k229225j.image.r=Lagrange%2C+Joseph-Louis%2C.langEN.f274.pagination ? 82.163.24.100 (talk) 19:39, 9 August 2009 (UTC)

The present Reference 3 should probably now link to http://gallica.bnf.fr/ark:/12148/bpt6k229225j/f819.image.r=lagrange.langFR . 94.30.84.71 (talk) 19:20, 12 June 2011 (UTC)

In the examples of L4 and L5, the link to "NASA's animated clip" doesn't go to the correct clip. — Preceding unsigned comment added by 69.70.154.110 (talk) 15:20, 18 July 2013 (UTC)

How about an explanation for the common man?

This article is clear as mud. — Preceding unsigned comment added by 158.61.0.254 (talk) 21:37, 18 July 2012 (UTC)

I think that at least the first sentence should be changed. "The Lagrangian points are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be part of a constant-shape pattern with two larger objects." is horrible. The problem is the "be part of a constant-shape pattern with two larger objects" bit. This might be the best general description of the phenomenon but it's difficult to understand. It should either be replaced with something that doesn't include the term constant-shape pattern, or immediately afterword there should be a paragraph explaining it. I would suggest something like: "The speed at which an object orbits around another is related to how close it is. The closer the two objects get, the faster the orbiting object must be. This means that distance between two objects orbiting the same celestial body at different altitudes can not remain the same with the exception of five points provided one of the orbiting objects is of negligible mass. At these five Lagrange points the gravitational attraction of the larger orbiting object on the object of negligible mass either reduces or increases the speed required to orbit the celestial body at a certain altitude by exactly the amount needed so the smaller object can have the same orbital period as the larger orbiting object at a different altitude." Now I realize that of course all three objects are orbiting a common center but to include that would make it unclear. Also I might be a bit wrong because I'm not a physicist. Especially suspect is the use of equidistance as a goal, which is probably only valid for circular orbits (I don't know if that is the case). If it isn't valid for elliptical orbits, perhaps relative angles should be used or circular orbits should be specified. I came here hoping to understand the concept and then clicked back and went to the ESA webpage on the subject because this article starts too abstract and then just gets very technical. I haven't made the modifications directly, because I could be partially or totally wrong. I would kindly request that someone with more knowledge of orbital mechanics check my paragraph and include it or a modified version of it. Kaanatakan (talk) 16:13, 22 October 2013 (UTC)

History and concepts

The section contains "The three collinear Lagrange points (L1, L2, L3) were discovered by Leonhard Euler a few years before Lagrange discovered the remaining two." That is doubly false.

The cited paper, E.327, deals with purely rectilinear motion and so cannot be said to have revealed the Lagrange Points. Euler did predict, in E.304, L1 and L2 - but not L3, though it is fairly obvious from what he wrote.

Lagrange did not discover any points, as he never wrote about setting one mass to near-zero, and moreover he wrote that he did not expect the situation to occur in nature (or, at least, involving the Earth). But the points are rightly named, since Lagrange's work provided the explanation of the objects later observed in the first decade of the twentieth century.

Before citing a paper, one should read and understand it in its original form, to ensure that it says what one wishes to assert that it says.

The article should give (for possible correction) the earliest use of "Lagrange" or "Lagrangian" in naming the points themselves.

94.30.84.71 (talk) 18:38, 25 January 2014 (UTC)

Swap Mission Colour Coding?

Would it not be more natural to colour the successful missions green and the in-progress missions yellowy orange? Currently they are the other way around. 31.52.5.40 (talk) 14:58, 2 April 2014 (UTC)

Graphs of effective potential

The article includes two three-d graphs of effective potential. The first is static, and (as far as I can tell) correct. The second differs from it in two important ways:

1. it is animated
2. it has the contour lines outside the orbit of the secondary body going the wrong way, so that instead of its main feature being the deep potential well of the primary, it is an unexplained ridge surrounding the primary.

I see little benefit from the animation. All it does is rotate. This is easy to envisage from a static diagram.

The second difference is seriously misleading. I suggest deleting the second diagram (and merging some of the content of its caption into that of the first), and will do so unless persuaded otherwise. Maproom (talk) 10:57, 25 December 2014 (UTC)

Script for plotting the centrifugal/gravitational force

If anybody wishes to replot the data or just play with the problem, the following python script may be useful: https://gist.github.com/FilipDominec/4d5067717cecb4f699ad It shows the overall force in the Sun-Earth system. --FDominec (talk) 05:17, 25 January 2015 (UTC)

Missing words

Sorry if I'm wrong on this, but are there words missing from the caption in the rotating diagram? It just ends "in relation to..." Thanks InspectorSands (talk) 01:27, 25 October 2009 (UTC)

 Done -- I'm not seeing a problem now. TNKS, Charles Edwin Shipp (talk) 00:26, 4 April 2015 (UTC)

The L2 distance

“ This distance can be described as being such that the orbital period, corresponding to a circular orbit with this distance as radius around M₂ in the absence of M₁, is that of M₂ around M₁, divided by ${\sqrt {3}}\approx 1.73$ ”

I think this says that the distance of Sun-Earth L2 from Earth is such that, if there were no Sun, a body at that distance would orbit Earth in 1/√3 year. Is that right? —Tamfang (talk) 19:04, 7 March 2011 (UTC)

Linguistically it says (subclause interpretation):

“ This distance can be described as being such that the orbital period is that of M₂ around M₁, divided by ${\sqrt {3}}\approx 1.73$. The orbital period corresponds to a circular orbit with this distance as radius around M₂ in the absence of M₁. ”

or (ellipsis interpretation):

“ The orbital period, corresponding to a circular orbit with this distance as radius around M₂ in the absence of M₁ is called PFHRRG. This distance, that can be described as being a PFHRRG, is that of M₂ around M₁, divided by ${\sqrt {3}}\approx 1.73$ ”

I cannot make any sense of it. Rursus dixit. (^mbork³!) 08:55, 30 July 2011 (UTC)

A proof of this follows the first part of http://www.merlyn.demon.co.uk/gravity4.htm#Ap1. 94.30.84.71 (talk) 12:28, 11 May 2012 (UTC)

"At the L1 point, the orbital period of the object becomes exactly equal to Earth's orbital period. L1 is about 1.5 million kilometers from Earth.[4]"
" ... at the L2 point that orbital period becomes equal to Earth's."

Since the distance of L1 from Earth is given, the distance of L2 should also be given. L2 is just as important as L1. — Preceding unsigned comment added by Martin Coles (talk • contribs) 00:12, 25 April 2015 (UTC)

Orbiting a Lagrangian point

I'd like to remind JorisvS of WP:BRD, which discourages reinsertion of edits that have been reverted without bringing it to talk first.

A body that orbits a Lagrange point still orbits the Sun as well (and the Earth too), so there is no inherent contradiction. How you describe it depends on your reference frame. Now clearly, a rotating reference frame is not an inertial one, but it's still an important conceptual tool. The point of the original wording is that in a rotating frame for the two dimensional problem, there are closed orbits that surround L4 and L5, which are equilibrium points in the rotating frame. Martijn Meijering (talk) 21:13, 20 May 2015 (UTC)

No, it doesn't. A Jupiter trojan does not orbit Jupiter. A body can only orbit a single other body (which can be composite, like in the case of a circumbinary planet, and that body can, in turn, orbit another body). Trojans, do not orbit the planet with which they are associated. It is a special case of a co-orbital configuration (which is, in turn, a special case of an orbital resonance), with gravitational interactions keeping the configuration intact. A trojan's trajectory with respect to its Lagrangian point is called libration, and can have all kinds of forms, as seen from a corotating reference frame, but are not ellipses (like orbits are). The description should be in a way that can be understood without making reference to a specific reference frame (unless describing the form of the trajectory in a specific reference frame). And Lagrangian points are equilibrium points regardless of reference frame: physics does not depend on one's reference frame. --JorisvS (talk) 08:45, 21 May 2015 (UTC)

Citation needed for the assertion that a body can only orbit a single other body. Clearly, if you are inside the sphere of influence of the moon, then the moon's gravity is the dominant force, so you might consider it more natural to say that you orbit the moon rather than the earth. Nevertheless, if you leave the moon out of the picture, it looks pretty darn close to an Earth orbit. On the other hand, if you are outside the moon's sphere of influence it is unreasonable to say that you are in lunar orbit, instead we say that the orbit is perturbed by the moon. If you are exactly at a stable Lagrange point, it is unreasonable to deny you are in a (perturbed) Earth orbit.

And for your information, the definition of an orbit doesn't require it to be elliptical (or even a conic section), it encompasses the phenomenon of libration too, hence the term libration *orbit*. Also, consider perturbed Earth orbits. The orbit of the ISS is an example of a lightly perturbed orbit, while low lunar orbits are strongly disturbed by the effect of mascons. It would be unreasonable to assert that these are anything else than orbits even though they are not elliptical.

Furthermore, a Lagrange point is most definitely *not* an equilibrium point for the equations of motion in an inertial frame, rather it corresponds to a circular (or elliptical) orbit. Once you switch to a rotating frame that rotates with the period of the circular orbit (i.e. roughly a month in the case of the Earth moon system), the periodic solution is transformed into an equilibrium solution. Both frames are used extensively in orbital dynamics.

If you have concerns about the wording, I'll be happy to work with you to accommodate them, but I don't appreciate your reinsertion of your edit over my objections, in violation of WP:BRD.Martijn Meijering (talk) 16:42, 21 May 2015 (UTC)

That's why I said that the body that is being orbited can itself orbit another body. And the trojans are actually far outside the SOI of the body they are associated with! And the orbit is actually a librating orbit: the orbit itself is a simple Keplerian that is gradually being perturbed by the larger body the trojan is associated with, causing gradual change (libration) of the orbit with the Lagrangian point as the average and a period much larger than their orbital periods. And if the equations of motion are integrated, the result has to be the same regardless of the reference frame one uses, so either they're equilibrium points, or they're not. Of course, in a non-rotating reference frame, the points themselves move along the orbit of larger body as it orbits the central one, and are hence time-dependent. I regularly employ an edit–revert–explain-revert–(rerevert–)discuss cycle for those cases where the edit is hardly "bold", but where the other editor has a hard time understanding the reason for the edit, because typically the explanation in the edit summary suffices (and hence then starting a new thread on the talk page is a waste of time and effort). --JorisvS (talk) 18:44, 21 May 2015 (UTC)

I never denied that a body that is being orbited can itself orbit another body, it is very obvious that it can. Also note that both 'librating orbit' and 'libration orbit' are correct, as a simple Google Scholar search will show. As for different frames having to give the same result: obviously they have to give *equivalent* results, but not *identical* results. A libration orbit is not an equilibrium solution in an inertial frame, rather it is a periodic solution. Consider L1 in the Earth moon system, seen from an inertial frame centered around the center of mass. Seen from above / below, the orbit of a spacecraft is almost circular, rotating with the same angular velocity as the moon, as opposed to the higher angular velocity that would be expected if it had moved only under the influence of the Earth at the same distance. In a corotating frame, the spacecraft appears to be stuck at a point, i.e. in an equilibrium orbit. See https://www.youtube.com/watch?v=cGm-nrgAIzM for an illustration. Bear in mind that in this video we are looking at Sun-Earth L1, not Earth-moon L1, but the principle is of course the same. Martijn Meijering (talk) 09:27, 23 May 2015 (UTC)

Perhaps you are confusing the term orbit, which is the actual trajectory a spacecraft is in with its osculating orbit, which is the instantaneous Keplerian approximation to that orbit. Martijn Meijering (talk) 09:37, 23 May 2015 (UTC)

Also check out this article for an explanation. http://www.wired.com/2012/12/does-the-moon-orbit-the-sun-or-the-earth/ Martijn Meijering (talk) 10:27, 23 May 2015 (UTC)

The video is misleading; it does not work like that. In fact, objects near the L1, L2, L3 even require periodic corrections to prevent them from drifting away. Objects near L4 and L5 do not, because a deviation from the point corrects itself. The Moon is unique among the known natural satellites in that it never appears to fall away from the Sun (its orbit is always convex), but it is still squarely within the SOI of Earth; trojans are not. Now, whether one uses the term "orbit" or not for trojans' association with Lagrangian points is, at the end of the day, just terminology. The fact remains that a trojan's trajectory/orbit/whatever with respect to its Lagrangian point is physically very different from that of a natural satellite, including the peculiar case of the Moon, and that's really my whole point. --JorisvS (talk) 13:56, 23 May 2015 (UTC)

I'm not sure what you're getting at. Periodic orbits of a *stable* Lagrange point (seen in a corotating frame) can be similar to the ones seen in a simple Keplerian system, though the details are different. No such orbits exist for the unstable ones, though there do exist three-dimensional halo orbits, which is worth pointing out. In any event, in the stable case it is entirely reasonable to describe the periodic orbits as orbiting the Lagrange point (in a rotating frame), and whether there is a physical object such as a spacecraft nearby is immaterial.

The video and the article I linked to correctly depict how an object can orbit one object (say the Earth) while at the same time orbiting another (say the sun), contrary to your earlier assertions. This is why I mentioned them. Yes, L4 and L5 are stable (in the idealised case, though not in the Earth moon system, due to the combined effect of the eccentricity of the moon's orbit and external perturbations), while the others are not. This is precisely why there are periodic solutions surrounding L4/L5 in a corotating frame, while no such solutions exist for the collinear points. This can be clearly seen in the plot of the effective potential (i.e. with the effect of the fictitious centrifugal pseudoforce due to the corotating frame accounted for) in the WP article.

Perhaps the article needs to do a better job of explaining the equivalence of equilibrium solutions in corotating frames and periodic solutions in inertial ones. Pointing out the relationship between general orbits and their instantaneous osculating Keplerian approximations would likely also be helpful. I'd also like an explanation that, depending on the reference frame, an object can reasonably be described as orbiting several different bodies.

Given that you've now made several demonstrably incorrect technical assertions it might perhaps be wise to be a bit more reluctant to reinsert changes you've made over the objections of others. Martijn Meijering (talk) 14:27, 23 May 2015 (UTC)

Whether or not there is a central body to orbit is hardly "immaterial", it makes the situation very different! If there is no object, there is no centripetal force acting on the body. "Perhaps the article needs to do a better job of explaining the equivalence of equilibrium solutions in corotating frames and periodic solutions in inertial ones." and "Periodic orbits of a *stable* Lagrange point (seen in a corotating frame) can be similar to the ones seen in a simple Keplerian system, though the details are different.": why don't you try me here!

"This is precisely why there are periodic solutions surrounding L4/L5 in a corotating frame, while no such solutions exist for the collinear points.". Collinear points have no movement associated with them, astronomical bodies and Lagrangian points move, which makes all the difference. The centrifugal force is a fictitious force to correct for the non-inertial reference frame. --JorisvS (talk) 16:39, 23 May 2015 (UTC)

"The video and the article I linked to correctly depict". The article, sure (I never said it didn't), but I can't fathom how you could say that about the video. Why don't you try me!

"Given that you've now made several demonstrably incorrect technical assertions": state them! (And don't talk about terminology, which really is immaterial, but the actual concepts and definitions involved.) --JorisvS (talk) 16:39, 23 May 2015 (UTC)

Problems with Equations for L3?

I think that for L3, the approximate value for r should be close to ~R, not R(7/12)(m2/m1). The exact equation given for solving for r diverges to infinity at r->R (the first term on the left: m1/(R-r)^2), so it's not going to work either. Synecdodave (talk) 12:30, 12 June 2015 (UTC)

Hey, SNAP! I just happen to have made a similar observation. Part of the trouble is that I cannot trust the wording of the article which says "r now indicates how much closer L3 is to the more massive object than the smaller object". If that means how much outside the Earth's orbit L3 is, OK, but if not, could someone who has worked it out please confirm that L3 is some 262500 metres outside (or inside) Earth's orbit? Or are we missing a cube root somewhere? Furthermore, I would have thought that if that were correct, then it should read something like "here r is how much further L3 is from the more massive object than the less massive object is from the more massive object; in other words how much greater the radius of the orbit of an object at L3 is than the radius of the orbit of the smaller mass"
(In my calculation I used masses of 2e30kg for Sol, 6e24 kg for Earth and 15e10 m for Earth's orbital radius, and assumed circular orbits.) That is such a tiny smidgin that since I was using approximate values and formulae, I could not confirm my values directly. That does not matter much but either the formulae given are wrong, or the wording is unclear, neither of which is tolerable in WP. If some kindly applied mathematician could confirm whether I have got it right, or if wrong, then how, then I would be grateful and would even would be happy to do some editing to make the article more intelligible. PLEASE? JonRichfield (talk) 16:06, 16 June 2015 (UTC)