Talk:Ladder paradox/Archive 1

Archive 1

Explanation

Part 1

At a first read the solution to this paradox seems hard to digest. Is it not that the very hypothesis of fitting the ladder in the garage is based on an observer at rest relative to the garage? If not so, then what does the "fit" mean?

To "fit" means that the entire ladder is contained within the garage with the doors closed. It is easy to see this from the reference frame of the garage. From the reference frame of the ladder itself this seems impossible until you realize that for the garage to contain the ladder it must bring the ladder to a complete halt within itself (make the ladder be at rest relative to the garage). In order for that to happen the ladder must be accelerated into the reference frame of the garage. The acceleration doesn't happen all at once but one part of the ladder at a time (think of a series of beads connected by springs), as is mentioned in the article.

Coincidentally, I've been thinking about including the original man falling into grate version because although the solution is simpler to visualize in the ladder and garage version (i.e. two-door garage) it's easier to visualize the application in the man and grate version (as opposed to the contracting ladder). DonQuixote 03:58, 21 May 2005 (UTC)

I have read the above explanation, and the explanation in the article and it is wrong. The ladder is "contained" in the garage if you are in the rest frame of the garage, but it is not "contained" in the garage when you are in the rest frame of the ladder. "Contained" is a relative term, not an absolute one. Two inertial observers can disagree over whether the ladder was "contained" just as they can disagree over whether two events were simultaneous. Use the idea of two doors which are initially closed, and the ladder is heading towards the garage. The front one opens just when front of the ladder enters, and the back one opens just when the front of the ladder exits. The front door closes just when the back of the ladder enters, and the back door closes just as the back of the ladder exits, leaving both doors closed. The ladder is "contained" if there is a point in time during which both doors are simultaneously closed after the first door has opened and then closed. "Simultaneously" is a relative term. It can very well be that what the person at rest with the garage says is simultaneous is not simultaneous with respect to the person on the ladder. That is in fact the case. Both people agree that each door opened and closed, they disagree on whether they were both closed simultaneously after the first door had opened and closed. The resolution of the paradox is not to show that both see the ladder as contained, but to show that "containment" is a relative term, not absolute.PAR 04:56, 22 Jun 2005 (UTC)

The ladder is contained in both reference frames -- so it's correct. The part that you have to understand is that the ladder has to accelerate into the reference frame of the garage and come to a complete halt with respect to it. Read Relativity: Special, General and Cosmological by Wolfgang Rindler. Come to think of it, I should probably include a link to it in the article (silly me). Also, don't mix up the two-door garage example with the one-door garage example. Yes, in the two-door garage example the ladder cannot be contained within the garage (the two-door example is used to illustrate the concept of relative simultaneity), however in the one-door example the ladder has to be contained within the garage in both reference frames, hence the ladder contracting under its own acceleration. DonQuixote 04:04, 22 Jun 2005 (UTC)

The weakness of this article is that it doesn't make a clear distinction between the case of the two-door garage (explanation: relativity of simultaneity) and the one door garage (explanation: absence of infinitely rigid objects in SR). Czyx (talk) 17:23, 10 January 2013 (UTC)

Both involve relative simultaneity. Absence of an infinitely rigid object is a result of this. DonQuixote (talk) 02:12, 11 January 2013 (UTC)

They are different phaenomena, you simply reverted the article to the original , weaker and more confusing form. — Preceding unsigned comment added by 24.4.101.48 (talk) 16:59, 14 January 2013 (UTC)

Absence of an infinitely rigid object is a result of relative simultaneity. This can be mentioned in the article (and was a conclusion of Rindler's original article), but the article as it stands is correct. DonQuixote (talk) 17:06, 14 January 2013 (UTC)

Rigidity is a material property. You are stretching the concept when you say it is a consequence of relativity of simultaneity. What you can say is that compression/stretching forces take time in order to propagate. I tried to clean up your article a bit but it looks like you are very stuck on the way you wrote it. So, good luck! — Preceding unsigned comment added by Czyx (talk • contribs) 20:30, 14 January 2013 (UTC)

Yes, rigidity is a material property, but the upper limit is a relativistic property. Length contraction dictates that there is no such thing as 100% rigidity. It's similar to engine efficiency. Engine efficiency is a function of the design of an engine, but thermodynamics dictates that there is no such thing as 100% efficiency. DonQuixote (talk) 21:31, 14 January 2013 (UTC)

Ok, we agree how things work in the "two door example", the fact that they disagree on whether the ladder is contained, right? But I don't get the "one door example". If you require that the ladder be contained in the garage in both reference frames, then yes, you have to crush the ladder to make it fit, because its rest length is longer than the garage, but its not going to crush itself. If the force of deceleration doesn't happen to crush it, then it won't fit, and there's no special reason that the force of deceleration should crush it, you may have to apply extra force to crush it. And theres no guarantee that once crushed it will spring back to its original rest length. What's the paradox? PAR 04:56, 22 Jun 2005 (UTC) (PS I will try to find Rindler)

Actually, it is going to crush itself. There is no such thing as a rigid rod in relativity. Here's where relative simultaneity comes into play. From the perspective of the garage, every point of the ladder comes to a halt within the garage simultaneously while from the perspective of the ladder, each point of the ladder comes to a halt within the garage sequentially. And it will spring back to its original length because it is not being physically crushed but relativistically crushed (i.e. trash compacter vs. relativistic length contraction). This is because during the acceleration (or deceleration), each point of the ladder occupies a different inertial reference frame as a result of the sequential acceleration. The paradox is that without this contraction there is no way a ladder will fit into a one-door garage from the perspective of the ladder. DonQuixote 14:04, 22 Jun 2005 (UTC)

I understand that there is no such thing as a rigid rod in relativity. As to the crushing force, there will have to be an external force applied to the ladder to make it come to rest in the garage frame, and this is the crushing force I am referring to. Lets say this crushing force is delivered by the (doorless) back wall of the garage when the front of the ladder hits it. Lets say that when the front of the ladder hits the back wall, it stops rather quickly. Simultaneously with that instant, the garage guy will say that the back end of the ladder is inside the garage, while the ladder guy will say that it is not. This is because they disagree on what is simultaneous. The collision event at the rear of the garage can only propagate its influence at the speed of light, no faster. Therefore, the back end of the ladder will continue on its course, unaffected by what happened at the head of the ladder. Eventually it will be influenced by the collision at the back of the garage, as the crushing effect moves along the ladder at less than or equal to the speed of light, as you say. At the instant the back of the ladder feels the effect of the collision at the front, it will be inside the garage. The point is, the ladder has been trash-compacter crushed by the force of the impact with the rear wall. Whether it now springs back to its original length or not depends on the physical characteristics of the ladder. I expect if it is wood, it would be quite damaged, and not resume its original condition.

To say it another way: If the rest length of the ladder never changes, then it will never fit inside the garage while it is at rest in the garage. Never. If different parts of the ladder are in different inertial frames, this is exactly, identically, the same as saying that it is being trash-compacter crushed. PAR 15:31, 22 Jun 2005 (UTC)

The problem is that you're thinking of the ladder as being in one inertial reference frame. It's not. If you were to stand at the back of the ladder, when the front part of the ladder accelerates into the reference frame of the garage it won't be in the same reference frame that you're in. The front part of the ladder doesn't physically get crushed, rather it undergoes a relativistinc length contraction. It appears to be crushed because you're no longer in the same reference frame as it is. Think of two ladders that are side-by-side. If one of them suddenly accelerates into another reference frame, it won't be trash compactor crushed but will be relativistically length contracted with respect to the other ladder. Instead of having them side-by-side we have them in single file, we'll have the same phenomenon. If we make the individual ladders smaller and smaller and put a large number of them in single file, then we'll have the ladder in a garage situation where the ladder itself isn't being trash compactor crushed but rather each individual part of the ladder is being length contracted at different times. In other words, from the perspective of the garage each part of the ladder is being length contracted simultaneously, however from the perspective of the ladder each part of the ladder is being length contracted sequentially. DonQuixote 16:54, 22 Jun 2005 (UTC)

Part 2

Ok - this is getting simpler. The definition of physically (trash-compacter) deformed is that at some instant, one part of the ladder is simultaneously moving at a velocity that is different from another part of the ladder according to someone at rest with some part of the ladder. (this is the person who defines "simultaneous"). Unless all parts of the ladder are simultaneously at rest with each other part, (again, according to someone at rest with respect to the ladder), then the ladder is being physically deformed at that time. Can we agree on this definition? PAR 18:19, 22 Jun 2005 (UTC)

PS - this excludes someone who is not in the rest frame of the ladder, who is watching it perhaps accelerate/decelerate, and undergoing the subsequent relativistic "sequential" or "non-simultaneous" length contractions/expansions.PAR 18:19, 22 Jun 2005 (UTC)

No, the definition of physical deformation (trash compacter) is that the rest length is changed. No such thing happens in the acceleration contraction of the ladder. The only time anything remotely like that happens is after the ladder comes to a complete halt in the garage and reverts back to its rest length where it is deformed by hitting the walls of the garage. DonQuixote 04:19, 23 Jun 2005 (UTC)

You could have the ladder's front half being crushed while its back half was stretched. There would be physical deformation, yet the rest length would stay the same. To be precise, there is no physical deformation only if all parts of the ladder have the same velocity, according to someone at rest with the ladder. (That velocity would be zero). It follows that the rest length is unchanging, but an unchanging rest length does not imply the absence of physical deformation. Its a good definition isn't it? PAR 05:01, 23 Jun 2005 (UTC)

You're just making it more complex that it has to be. It's like assuming a cow is spherical and spurts milk isotropically to make the calculations easier. Similarly, assuming a ladder that doesn't change its rest length makes understanding this problem easier. The bottom line is that the rest length of our simple ladder doesn't change and therefore it doesn't get crushed physically; the only thing that happens is that it undergoes a relativistic length contraction (simultaneously with respect to the garage and sequentially with respect to the ladder). DonQuixote 20:47, 23 Jun 2005 (UTC)

When you say "sequentially with respect to the ladder" are you saying that, according to someone sitting on the ladder, there is some point in time when part of the ladder is relativistically contracted, and part of the ladder is not? PAR 20:58, 23 Jun 2005 (UTC)

Yes, exactly. DonQuixote 03:21, 24 Jun 2005 (UTC)

Then (with respect to the ladder person) the part of the ladder that is relativistically contracted is travelling at a different velocity than the part that is not. right? PAR 05:19, 24 Jun 2005 (UTC)

I know what you're trying to get to, and the answer is that it's still not being physically crushed. Look, the thing is that all this takes place in a split second and what we're interested in is the part that happens before anything physical happens to the rest length of the ladder. In that split second it's purely relativistic. It's like assuming a frictionless surface in order to assess the equations of motion of a moving object. Similarly, we're disregarding any crushing effects and are focusing directly on the relativistic effects. Another way of looking at it is that instead of a ladder made out of paper or aluminum, we're considering a non-crushable super-strong material. This material cannot be physically crushed, ever--i.e. it's the extreme case scenario. Even with this indestructible material, the ladder will undergo a relativistic length contraction: simultaneous in the garage rest frame and sequential in the ladder rest frame. DonQuixote 18:33, 24 Jun 2005 (UTC)

I'm just trying to nail down where we disagree. I know that you know what I'm trying to get to, but how do you answer the above question? I think its a reasonable question. Is it right or wrong? PAR 19:34, 24 Jun 2005 (UTC)

It's both right and wrong. From the perspective of the garage, the every part of the ladder is travelling at the same speed and every part of the ladder accelerates simultaneously into the reference frame of the garage. From the perspective of the ladder, every part of the ladder is travelling at the same speed but each part of the ladder accelerates at different times, and therefore have different speeds, when it accelerates into the reference frame of the garage. However, as stated above, this doesn't mean that the ladder gets physically crushed (the non-crushable material). Rather, the ladder undergoes a relativistic length contraction. In other words it's saying that there is no such thing as a rigid object in relativity because even a non-crushable object (something that cannot be trash compacter crushed) will under go length contraction. DonQuixote 20:30, 24 Jun 2005 (UTC)

It's a clear, unambiguous question. It cannot be both right and wrong. From what I understand, you are saying that it's right, different parts of the ladder have different speeds at some instant in time with respect to an observer at rest with some part of the ladder, and that this does not imply physical deformation of the ladder. Is that right? Because if it is, we have nailed down the basic nature of the disagreement. PAR 21:01, 24 Jun 2005 (UTC)

From the reference frame of the ladder it's right; from the reference frame of the garage it's wrong. It can be both right and wrong based on the observer. The problem with common every-day speed and acceleration is that it's not a true relativistic vector and therefore variant based on the observer. That's why we have things like time-dilation and length-contraction. That's why rods appear to bend and and distort. The ladder only appears to deform but it isn't actually deforming. Look, as stated above, if we start out with an invulnerable ladder--one that's not subject to being crushed, even with this miraculous highly indestructible thing, given the sitation, this thing will still appear to be crushed. It's not being physically deformed, since we have specifically stated that that is impossible, so something else is going on. That something else is just relativistic length contraction. Forget speeds, forget accelerations--what we have is an uncrushable object that appears to have been crushed. DonQuixote 04:57, 25 Jun 2005 (UTC)

The question was:

"Then (with respect to the ladder person) the part of the ladder that is relativistically contracted is travelling at a different velocity than the part that is not. right?"

The question has always been framed with the proviso that it was with respect to someone at rest somewhere on the ladder, so I take it you are saying that it is right. This is the crux, the central core of the disagreement. I understand that the relativistic contraction is just an appearance, not a physical distortion. The thing that makes all the difference is the simultaneous presence of different distortions (according to the ladder person). Relativistic distortion is a function of velocity. If the ladder person sees one piece of the ladder contracted and another piece uncontracted, then it is absolutely certain that those pieces are moving at different velocities. This difference in velocity is the very definition of a physical distortion in progress. If all parts were equally contracted, they would all have the same velocity, and there would be no physical distortion although there would be a relativistic contraction.

To say it a different way, just because two relativistic distortions are each an "appearance" does not mean that the fact that they are different is also an "appearance".

Sorry, I haven't read through the complete discussion above, but I believe that it is not necessary to invoke the notion of acceleration; the ladder doesn't have to come to a halt in my understanding. Specifically, I disagree with the statement

for the garage to contain the ladder it must bring the ladder to a complete halt within itself (make the ladder be at rest relative to the garage)

In my view, the question is simply which of the following two events happens first:

• event A: the front of the ladder crashes into the end of the garage
• event B: the end of the ladder enters the garage

Both observers agree to say that "the ladder fits" if and only if event A happens after B. The two observers simply disagree which of the two events occurs first (because of relativity of simultaneity), so we conclude that the statement "the ladder fits" is also relative and both observers are correct to reach opposite conclusions. AxelBoldt 20:25, 25 Jun 2005 (UTC)

Hello Axel - Thanks for responding to our discussion - I know we have generated a lot of verbiage but I think I can summarize as follows: (Please correct me if I'm wrong, DonQuixote)

• There are a number of versions of the ladder problem. You have described what I will call "ladder paradox 1". I think we all agree on the nature and solution to this problem.
• What we are discussing is what I will call "ladder paradox 2" and whether it is indeed a paradox. This consists of assuming that once the ladder is contained in the garage, (according to the "garage guy" who is at rest with respect to the garage), it then experiences, at each point, simultaneously, an equal deceleration which brings the ladder to rest inside the garage. Again, this "simultaneous" is with respect to the garage. In the ladder frame of reference, this deceleration will not be simultaneous, but "sequential". The question is, does the ladder undergo a physical deformation during this deceleration, and what happens after the deceleration is complete?

I have put two headers on the discussion (part 1 and part 2). Part I think delineates the initial part of the discussion where I didn't really understand the nature of the disagreement. Part 2 is where we zero in on the exact nature of the disagreement. If you have time to read and comment on part 2, I think we would both appreciate it. PAR 22:54, 25 Jun 2005 (UTC)

"Consider the admittedly unrealistic situation of a man carrying horizontally a 20-ft pole and wanting to get it into a 10-ft garage. He will run at a speed $v=0.866c$ to make $\gamma =2$, so that the pole contracts 10 ft. It will be well to insist on having a sufficiently massive block of concrete at the back of the garage, so that there is no question of whether the pole finally stops in the inertial frame of the garage, or vice versa [note: in the article I just generalized it to an undefined acceleration]. So the man runs with his (now contracted) pole into the garage and a friend quickly closes the door. In principle we do not doubt the feasibility of this experiment; that is, the reality of length contraction. When the pole stops in the rest-frame of the garage, it will tend to assume, if it can, its original length relative to the garage [emphasis mine]. Thus, if it survived the impact, it must now either bend, or burst the door, or remain compressed [i.e. trash-compacter crushed]."--Wolfgang Rindler, Relativity: Special, General and Cosmological pg.63

Also, the ladder fitting "if and only if event A happens after event B is wrong", unless you change event A to "the front of the ladder exits the other end of the garage". And the two observers don't "disagree which of the two events occurs first" (at least not in the way that its being referred to). The disagreement arises because the garage sees both events occuring simultaneously while the ladder sees event A occuring before event B (relative simultaneity). DonQuixote 08:06, 26 Jun 2005 (UTC)

Hello DonQ - I have rearranged the Ladder paradox page in a way I dont think you will disagree with. I separated into 3 parts, and put in some explicit calculations and a Minkowski diagram for the garage with two doors problem. I have left the second part, that we are discussing, alone. I modified the Minkowski diagram to illustrate the situation we are discussing. These are shown below, with my argument. We have to discuss this more quantitatively, and the Minkowski diagram is the way to do it.

You have introduced above a new twist - the idea that the ladder stops as a result of collision with the rear wall. This is different than saying all of its points stop simultaneously in the garage (in the garage reference frame) This is because the effects of the impact can only travel at the speed of light or less, so the deceleration will be sequential in the garage frame. I'm not sure which we want to discuss so I diagrammed both. Also you introduced events A and B and I don't know what they mean.

With regard to the quote by Rindler, read the sentence after the highlighted one - "Thus, if it survived the impact, it must now either bend, or burst the door, or remain compressed [i.e. trash-compacter crushed]". remain compressed - this means it is compressed, i.e. physically deformed. This is my point - Rindler says it is compressed, I say it is compressed, the Minkowski diagrams say it is compressed (in the green regions). The compression is real, not apparent. There is no way that a 12 foot ladder can be at rest inside a 10 foot garage without being physically trash-compacter compressed! Not even for an instant! If you still disagree, please, lets get quantitative and tell me where the Minkowski diagram(s) are wrong.

Figure 1 - This is the case where the ladder is stopped by impact with the back wall of the garage. The ladder is in red, the garage in blue. Everything simultaneous to the garage guy is parallel to the x axis. Everything simultaneous to the ladder guy is parallel to the x' axis. The impact is event A. At impact, the garage guy sees the ladder as AB, the ladder guy sees it as AC. The ladder does not move out of the garage, so its front end now goes directly upward, through point E. The back of the ladder will not change its trajectory in space-time until it feels the effects of the impact. The effect of the impact can propagate outward from A no faster than the speed of light, so the back of the ladder will never feel the effects of the impact until point F or later. When the back of the ladder enters the garage at point D, the ladder guy will see the ladder as DE. It is seen that this length is not the same as CA. The ladder is being crushed physically everywhere in the green region.

Figure 1 - This is the case where the ladder is stopped all along its length, simultaneously in the garage frame. Again, when back of the ladder enters the garage at point D, it has not yet felt the effects of the deceleration. According to someone at rest with respect to the back of the ladder, the front of the ladder will be at point E. Again, when the back of the ladder enters the garage at point D, the ladder guy will see the ladder as DE. It is seen that this length is again not the same as CA. The ladder is being crushed physically everywhere in the green region.

"Remain compressed" means that the length contraction compressed ladder becomes a trash compacter compressed ladder as the walls of the garage physically deform it when it returns to its rest length. The ladder is still not being crushed physically until after the event. In the Minkowski diagrams, CA is the rest length of the ladder but DE is not the rest length just like BA is not the rest length. This is because, just like the object described by BA is in a different reference frame from the garage, each part of the object described by DE are in different reference frames. That is, the green area is relativistically length contracted and if you mathematically uncontract it you'll get a length (rest length of that section) which you add to the length of the non-contracted part of the ladder to get the rest length. I'll sit down and work on the quantative description during any free time I have this week. DonQuixote 28

June 2005 14:05 (UTC)

Yes, thats an excellent idea, we have to get quantitative, because this qualitative discussion is not doing it. Just to respond to the above:

• You say: Remain compressed means that the length contraction compressed ladder becomes a trash compacter compressed ladder as the walls of the garage physically deform it when it returns to its rest length. I cannot make sense of this, we need a diagram. Especially since you have changed the definition from what you wrote previously: Thus, if it survived the impact, it must now either bend, or burst the door, or remain compressed [i.e. trash-compacter crushed].

Does it "remain" or "become" trash compacter compressed?

• You say: The ladder is still not being crushed physically until after the event. I agree totally. If you are saying that yes, the ladder is crushed after it hits the back wall, but is purely relativistically contrancted beforehand, then I fully agree and we have no argument.

• You say: In the Minkowski diagrams, CA is the rest length of the ladder but DE is not the rest length just like BA is not the rest length. This is because, just like the object described by BA is in a different reference frame from the garage, each part of the object described by DE are in different reference frames. Yes, CA is the rest length of the ladder because it is parallel to the x' axis. BA is not the rest length, because it is parallel to the x axis. It is the length according to the garage. DE is the length of the ladder accoding to someone at rest with the back of the ladder. (i.e. not in the green region). In the green region only, different parts of the ladder are moving at different velocities.

• You say: That is, the green area is relativistically length contracted and if you mathematically uncontract it you'll get a length (rest length of that section) which you add to the length of the non-contracted part of the ladder to get the rest length.. The rest length of the ladder is the length of the ladder when all of its parts are at rest with respect to each other, according to an observer that is also at rest with those parts. If different parts of the ladder are moving at different velocities then
  • The ladder is not at rest
  • Its rest length is undefined
  • It is being physically deformed

This is an important point, please let me know if you agree or disagree with all or part of this last point. PAR 28 June 2005 15:30 (UTC)

Does it "remain" or "become" trash compacter compressed?

It remains compressed by becoming trash compacter compressed. I.e. it was length contraction compressed but has become trash compacter compressed. And don't forget that the other two possibilites were that the ladder buckles or garage door bursts. So becoming trash compacter compressed is only one possibility. If the ladder were truly physically deformed during the event, then the other two possibilites would be impossible as it's rest length would already have been changed because of the compression.

If different parts of the ladder are moving at different velocities then

• The ladder is not at rest
• Its rest length is undefined
• It is being physically deformed

Yes, the first two points are correct. But if we examine each section of the ladder at the ladder's instantaneous inertial reference frame (i.e. references frames corresponding to the instantaneous velocity), then each part of the ladder has its own rest length. These rest lengths do not change. Being physically deformed means that these rest lengths are changed. That's why there isn't any physical deformation during this event. That's the point, you're confusing relativistic compression (where the lengths only appear to change while the rest lengths remain constant) with physical compression (where the rest lengths are changed).

DonQuixote 29 June 2005 16:00 (UTC)

I agree that a ladder could have different parts moving at different velocities, and still not be physically deformed. My point is that this can only occur for an instant. If the ladder is undeformed at time t and different parts have different velocities, then at time t+dt, it will be physically deformed. Do you agree with that? PAR 29 June 2005 18:04 (UTC)

I think this page needs some revising there are several resolution of the paradox each with their own section.--SurrealWarrior 2 July 2005 04:25 (UTC)

Sorry it's taking me so long to work it out quantitatively, but I'm a little swamped with teaching summer classes right now and my free time is rather low. DonQuixote 18:53, 24 July 2005 (UTC)

Why should we have an example with so complicated numbers. I suggest a model that both the ladder and garage are of the length 10 ft, and moving relatively to each other at the speed 0.6c, then the calculation will become much easier. I suppose the simplified model will be more friendly to the beginners. (Youyz (talk) 06:06, 23 August 2009 (UTC))

Minor change, Major change.

Removed the word "clearly" from the phrase the situation is clearly illustrated. For most people the Minkowski diagram is clear, and telling them it's clear is pointless. I'm not saying anything against the diagram by removing the word. But for some people (a small minority I'm sure) it will not be clear. They will have to work hard to understand it, and telling them it's clear will be unhelpful, making them think that they should be able to understand it without effort.

I hope this is okay. Today is the first day I've looked at Wikipedia properly (I haven't got an account yet) and on checking out SR discussion page it says you need help with the ladder paradox.

I'm only a relativity student, so I'm not going to make the substantive change myself. As I see it, the premise that the ladder can be brought to a simultaneous halt in the frame of the garage is where the problem starts. Arranging for every part of the ladder to be "simultaneously" decelerated is conceptually complex and should be way beyond the scope of this page. It would have to be an effectively infinite deceleration with the origin of the garage frame clearly defined. I think (although I haven't worked it out) that DonQuixote is correct that in this case the physical crushing occurs after the deceleration, as the deceleration itself causes comparable length contraction to the original velocity.

However for people interested in SR paradox resolution, the effect they want to understand is the ladder hitting the wall and that causing the deceleration, which leads to a physical crushing effect and the ladder breaking. The ladder never comes to a simultaneous halt in the frame of the garage as it is broken long before then.

If you want a simple explanation, consider the back end of the ladder at the time the front end hits the wall (in the frame of the garage). The information that the front end has hit takes a time to reach the back end (as the force's effect can't travel faster than c) and so it will just keep going at speed v until the force reaches it. I suspect that the force will actually travel at the speed of sound in the ladder. The front end stopped, the back end moving, something's got to give. If it isn't the wall, it's the ladder.

Hope this helps. Jon Hurwitz

Hi Jon - With regard to the statement that "simultaneous" deceleration (simultaneous in the garage frame, that is) is complex and infinite: Yes, it would be a complicated matter to make this happen, but the deceleration would not have to be infinite, just quick enough to keep the ladder in the garage. The physical crushing does not occur after the deceleration, the deceleration and the crushing are one and the same. Since the deceleration IS simultaneous in the garage frame, it therefore IS NOT simultaneous in the ladder frame. The deceleration in the ladder frame works its way along the length of the ladder. It takes a finite time for the deceleration to complete in the ladder frame. You simply cannot look at a ladder at rest, then watch different parts of it accelerate (change velocities) at different times, and deny that it is being physically deformed. The very definition of physical deformation is that different parts move at different velocities simultaneously in the rest frame. Right? PAR 13:22, 22 August 2005 (UTC)

Hi, PAR. Yes, I agree that the acceleration would not have to be instantaneous. I was thinking it would happen as the ladder touched the far wall, but if (in the garage frame) it was after B and before A, the deceleration would not have to be infinite. That it is not simultaneous in the ladder frame is beside my point. And so what if we disagree? This too is beside my point. You may well be right. You and DonQuixote can argue it out.

I am suggesting you abandon the idea of having the ladder decelerate simultaneously in the garage frame. Then the problem goes away (to return should you knowledgeable people ever agree). I'm saying it's not what people want to know from this page. It is a complicated, counterintuitive case.

If you let the ladder crash into the far end, there is no argument; the ladder breaks, you wrap up the paradox nicely and everyone goes home happy.

Cheers, Jon

Ok, I see what you are saying. I'm still arguing with DonQ I guess. But I think you have a good idea there. What changes would you make to the article, in a bit more detail? PAR 18:16, 22 August 2005 (UTC)

I think the bulk of the article is fine as far as I’ve read it. It’s just the resolution I think needs work. I’m not sure I’m the right person to write it, but here’s a first stab at an update. It'll need someone else to do the spacetime diagram. I'm pretty so-so on those.

"When the stationary garage traps the moving ladder, what happens after the event is either 1) the ladder continues out the other side of the garage (the above two-door garage example) or 2) the ladder is prevented from leaving the garage by the back wall. Considering just the latter: in the frame of the garage, the front of the ladder hitting the back wall, event A, occurs after the back of the ladder enters the garage, event B. The effect of the impact on the front of the ladder is not transmitted to the rear instaneously; it takes time, as nothing travels faster than the speed of light. During this time the rear of the ladder travels forward, compressing the ladder causing it to break.

From the frame of the ladder, the garage rushes forward, the back wall hitting the front of the ladder, event A, before the entrance of the garage passes the rear of the ladder, event B. But once again the effect of the impact does not reach the whole of the ladder immediately. It is impossible to accelerate the rear of the ladder by pushing on the front in less time than it takes light to travel the length of the ladder. By that time the entrance of the garage, travelling at v, has already passed the rear of the ladder, event B, and the front of the ladder has been compressed by the wall of the garage. The compression will cause the ladder to break at the front end before the rear of the ladder has had chance to move.

So in both frames the ladder and the wall collide and the rear of the ladder enters the garage. In both frames the ladder breaks. Only the order of events differs due the relativity of simultaneity."

--JonHurwitz 20:56, 22 August 2005 (UTC)

The discussion of the ladder being decelerated and crushed is irrelevant. After all, there is no paradox whatsoever in crushing something so it fits into a smaller space; the Ladder Paradox is that it can "fit" without being crushed! This discussion perhaps better belongs in a topic on Rigid Bodies in SR or the like. Lexchis (talk) 21:29, 1 January 2014 (UTC)

On stopping the ladder

I have been asked to put in my "two cents" on this, so here it is.

The real issue is this: If there is only one door to the garage and an impenetrable wall on the other side, can you be guarenteed a time when you can shut the door? The answer is "yes". Never mind whether the rod is crushed or not. As has been noted above, there is no such thing as a classically rigid rod in relativity. The issue now is why that is the case.

Look at it this way: When the front of the rod hits the far wall of the garage, how does the back of the rod know that this has happenned? The answer is that it does not! The back of the rod will continue to move forward until it receives a signal that the front has hit something and been accelerated by it. Such a signal will travel at the speed of sound through the rod. However, in relativity no signal can travel faster than lightspeed (c). So look at where back of the rod would receive the signal that the front has hit if it was traveling at c in both frames of reference. You will find that the rod must end up fitting within the garage in either case. At that point, my advice is to close the door quickly and hope that this is not a perfectly elastic rod such that it may spring back and ruin your nice door. --EMS | Talk 03:23, 23 August 2005 (UTC)

How to make a 20' ladder fit into a 10' garage

1. Simultaneously (from the point of reference of the ladder) accelerate all points of the ladder to a speed $v=0.866c$ relative to the garage.
2. Simultaneously (from the point of reference of the garage) decelerate all points of the ladder to a stop.

From the point of reference of the garage the acceleration is not simultaneous and manifests as a crushing force that shrinks the ladder to 10' in step 1, and from the point of reference of the ladder the deceleration is not simultaneous and manifests as a crushing force that shrinks it to 10' in step 2, and there is no paradox. --80.175.250.218 13:26, 9 November 2005 (UTC)

More on the "Resolution of the paradox if the ladder stopsesolution of the paradox if the ladder stops"

I think this section needs to be rewritten as the way it is now conflates the two reference frames. For example, it starts talking of the "stationary garage" implying the garage's reference frame (RF_g), but when it switches to the ladder's reference frame (RF_l) in the 4th sentence, it claims that "what the ladder experiences is one end decelerating..." But note that in RF_l, the experience is of a stationary ladder with the garage moving towards it, so this is incoherent. This confusion continues throughout the rest of the paragraph (with phrases like "catches up to"). I'm not sure the best way to reword things, but the discussion should probably consistently be from the point of view of RF_g. I may give it a shot though... —Preceding unsigned comment added by 74.98.19.154 (talk • contribs)

Re: changing reference frames in the 4th sentence: "Considering just the latter, we can say that every point of the ladder is simultaneously at rest from the perspective of the garage. From the perspective of the ladder this cannot be true." So it's not an incoherent shift. Read that last sentence carefully.

As to the ladder "catching up to" the garage, from the perspective of the garage the ladder stops within the garage. From the perspective of the ladder, each part of the ladder (starting from the right) independently accelerates to "catch up to" the garage. We are still in the reference frame of the ladder--more specifically the leftmost part of the ladder which hasn't accelerated yet.

DonQuixote 19:43, 23 June 2007 (UTC)

Thanks. I think your changing it from "decelerate" to "accelerate" made it a lot clearer too. (I just tried to help a little more with the ending too.)

Small things

Open before and after

Closed before

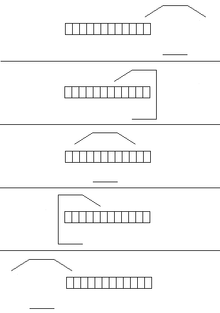
1. Is it a barn or a garage? Barns are usually big and can have two doors on opposite sides. Garages are usually small things with one door for a car.
2. Why are the doors open before the ladder approaches? I think this is more clear. Correct me if I am misunderstanding. — Omegatron 17:35, 23 June 2007 (UTC)

Response:

1. It could be either one. It could be a shed, for all we care. Rindler prefers using a garage. Some authors prefer using a barn. All we need is some building and some long pole-like thing. In fact, the original version involved a man falling into a grate. No ladder or garage there. However the original version is a little harder to visualize, so it's been turned into a ladder/garage (or ladder/barn) problem.
2. Having the garage doors open or closed before and after doesn't make much of a difference. However it might be easier to understand the diagrams if the doors started out as open. If you look at the other diagram (from the garage's perspective), you'll see that both doors start out as open, both close at the same time, and finally both open at the same time. Also, it reduces the number of drawings required. In your "closed before" diagram, you have to include an additional panel before the first where both doors are closed and an additional panel after the last where both doors are closed.

Hope this helps. DonQuixote 19:34, 23 June 2007 (UTC)

1. Yeah, but both are used. Pick one and stick to it.
2. Both doors are not closed at the beginning; just the opposite one. I think it makes the diagram easier to follow. Doesn't really matter, though. — Omegatron 01:38, 24 June 2007 (UTC)

Response:

1. Er...yeah, if you read carefully, only the garage is used. The barn version is mentioned within parentheses.
2. Again, that just creates complexity. The point is that the other diagram (from the garage's perspective) both doors close simultaneously and open simultaneously, and they do that only once. Can't get simpler than that. DonQuixote 07:15, 24 June 2007 (UTC)

I agree with critics that it is far clearer to start with the right door closed and have it open as the right end of the ladder approaches. In the garage/barn rest frame, the left door closes at the same time as the right door opens. In the ladder rest frame, the right door opens before the left door closes. In other words, one change of state for each door, and the key question is whether these are simultaneous or not. Having each door flap closed and open is just confusing. --Lexchis (talk) 21:21, 1 January 2014 (UTC)

The SVG version of some figures

Some of the figures are in the png format, and are suggested to be replaced by those in the svg format. So I have prepared some figures in the svg format. We can discuss if any further mordifications are needed.

Figure 1: An overview of the garage and the ladder at rest.

The figures are made according to the settings in the article. The length of the garage is 10ft, and the length of the ladder is 12ft. They are moving relatively to each other at the speed of $v=c/{\sqrt {2}}$. Figure 1 is an overview of the garage and the ladder.

Figure 2: In the garage frame, the ladder undergoes length contraction and will therefore fit into the garage.

Figure 3: In the ladder frame, the garage undergoes length contraction and seems too small to contain the ladder.

Figure 2 is the view from the garage frame in which the ladder is contracted by the factor root 2. Figure 3 is the view from the ladder frame in which the garage is contracted by the factor root 2. The question marks indicates that it will be problematic to think of the two doors closed simutaneously in the ladder frame.

Figure 4: Scenario in the garage frame.

Figure 5: Scenario in the ladder frame.

Figure 4 and 5 show the scenario in both frames respectively. The following events are depicted: (a) right end of the ladder passes the front door, (b) left end of the ladder passes the front door, (c) the front door closes and opens, (d) the back door closes and opens, (e) right end of the ladder passes the back door, (f) left end of the ladder passes the back door. The lengths and the positions of the ladder and garage in each picture is calculated according to the settings in the article. Everett (talk) 08:55, 23 August 2009 (UTC)

The only thing that I can suggest is to make the ladder longer (especially in figure 1) to emphasize the problem more. Other than that, I have no problem with these replacing my crude line drawings. DonQuixote (talk) 13:25, 23 August 2009 (UTC)

Thanks for the suggestion. I have shifted the ladder and closed the back door so that it will be obvious that the ladder is longer than the garage. I do not wish to exaggerate the length of the ladder. The distance between the neighboring rungs of the ladder is 1ft. So you can read from Figure 1, that the ladder is 12ft, and the garage is 10ft (the distance from front wall to back wall), which is in accordance with the settings in the article. Everett (talk) 21:29, 24 August 2009 (UTC)

Wrong?

I've got a question:

The article says that the garage would get smaller from the point of view of a person sitting on that ladder. But since there is length contraction happening to that person and since the eyes of that person shrink, shouldn't the garage get larger for that person? Because if it got, I wouldn't see any problem for that ladder to fit into the garage (supposed the ladder moves fast enough). —Preceding unsigned comment added by 217.227.123.77 (talk) 02:24, 26 March 2008 (UTC)

The point is that it's not happening all at once. If you sit at the back of the ladder, as the front of the ladder accelerates into the reference frame of the garage the front of the ladder will appear to shrink into an already small garage. That's the simplest case to imagine. If you're sitting at the front of the ladder, you accelerate into the reference frame of the garage first, that is, to you the garage has expanded to its full size. This also means that, to you, the back of the ladder appears shorter to you now and it is already within the garage. DonQuixote (talk) 14:13, 26 March 2008 (UTC)

Theres no such thing as a "Lorentz expansion". In other words, two people moving at different speeds will each see the other contracted. As mentioned above, the contraction is accompanied by a loss of simultaneity as well, and if you forget about this, there will be an apparent paradox. PAR (talk) 17:12, 26 March 2008 (UTC)

The article seems to use Special Relativity incorrectly right from the outset. Eg: from the point of view of the garage, the approaching ladder would not appear shorter than its stationary length, it would actually appear elongated (the opposite is claimed in the article). Similarly, from the POV of the approaching ladder, the garage would also appear elongated as it got closer. Any apparently paradoxical effects would have to rely on conflicting accounts from two different observers, but the illustrations in the article clearly place the reader as some kind of god-like observer at right angles to the action, which is absurd. --Guid123 (talk) 09:45, 3 November 2008 (UTC)

Sorry, you got that backwards. It's called "length contraction". The approaching ladder would appear shorter, etc. The illustrations are from the POV of the two inertial reference frames and not some "god-like" entity. From the IRF of the garage, the ladder would be contracted. From the IRF of the rear-most point of the ladder, the garage would be contracted and the front part of the ladder will contract due to accelerating into the IRF of the garage. DonQuixote (talk) 18:27, 3 November 2008 (UTC)

Just a question...

Was there ever a poem about this? I thought I saw one once, but I have not seen it since. If anyone goes on this page, sees this, and knows where the poem is, please respond on my talk page. Thank you. --Freiberg, Let's talk!, contribs 14:23, 8 December 2008 (UTC)

If I recall correctly, it was a poem about the twin paradox. DonQuixote (talk) 02:33, 9 December 2008 (UTC)

Lets remove "Man falling into grate"

The "Man falling into grate variation" should be removed, it is overly complicated and a proper resolution of the paradox will involve non-inertial frames of reference and mechanical behavior of the "man". It is not, at present, resolved, and the present discussion serves only to cloud the issue. The present section does not address the rotation aspect of the problem, which is presented in the simpler "bar and ring" paradox. I will remove this section soon if no one has an objection. —Preceding unsigned comment added by PAR (talk • contribs)

I object to it since it's the original version of the Ladder paradox. The main point, outlined in the diagrams, is that the relative simultaneity results in the rod falling simultaneously in one IRF while the rod follows a curved path in another. We don't need to address non-inertial frames or rotation or "stiffness" or whatever since they needlessly complicate the matter. DonQuixote (talk)

But "curved path" immediately implies a non-inertial frame of reference. A curved path in one inertial reference frame (IRF) will be curved in any IRF. If the rod is bent in one IRF, then it will be bent in any IRF. If the rod follows a curved path in any IRF, then the rest frame of the rod is not inertial. You cannot avoid the non-inertial aspect of the problem, and I agree, its a needless complication. Furthermore, the rotation aspect of the problem is ignored in the grate variation section (see rod and ring paradox), yet it is one of the major factors in the resolution of the grate paradox. The grate paradox is simply NOT resolved in this article. PAR (talk) 16:18, 13 September 2009 (UTC)

Inertial reference frames are independent of objects. The grate corresponds to one IRF, say IRF1. The moving rod corresponds to another IRF, say IRF2. The moment that the rod follows the curved path it accelerates from IRF2 to another IRF. However, IRF2 is still a valid IRF and it is with respect to IRF2 that the rod follows a curved path.

The point of the paradox is "does fit in vs does not fit it". The point is that objects will fit because of non-simultaneity and through contraction through acceleration or bending through acceleration. DonQuixote (talk) 16:49, 13 September 2009 (UTC)

Yes, but thats the point. The paradox must be resolved by 1) investigating the non-inertial behavior of the rod, 2) investigating the bending of the rod (which will involve the mechanical response of the rod to stress), and 3) the relative rotation of the grate and the rod in the grate IRF. None of these factors can be ignored when and if the paradox is resolved. As it stands the paradox is not resolved. It needs to be resolved or removed. PAR (talk) 17:09, 13 September 2009 (UTC)

1) The path is the non-inertial behaviour of the rod. 2) Assume the rod to be a mono-atomic filament. That is, the important part is the path (or more precisely, the kinematics). 3) The rotation is inherent within the path. DonQuixote (talk) 17:16, 13 September 2009 (UTC)

I don't understand any of that. Could you give more detail, I mean, be more explicit? Thanks. PAR (talk) 19:55, 13 September 2009 (UTC)

(Deindent) Going back to Physics I, in kinematics we describe paths through space that objects travel along, such as the parabolic path or circular path. The thing is that, instead of physical objects themselves (ie, shapes and moment of inertia tensors), we assume that they are point particles and that is how they travel along these perfect mathematical paths. In this problem, we do the same thing except now it is a string of point particles that we solve for and the curved path is a result of relativistic effects (relative simultaneity) instead of the downard acceleration itself. Read Rindler's article. DonQuixote (talk) 12:15, 14 September 2009 (UTC)

There is a quantitative solution to this problem, we don't have to go back and forth talking generalities. Please draw a Minkowski diagram of the grate paradox. It doesn't have to be perfect, just the general idea. PAR (talk) 20:20, 14 September 2009 (UTC)

If you want the quantitative solution, then read Rindler's paper [1] (he, more precisely, states that the path of the bending rod is a parabola). As this article is written now, it's adequate because it summarizes the main result which is the historically important part. If you want to expand it, go right ahead. DonQuixote (talk) 13:33, 15 September 2009 (UTC)

That link is not working for me, could you check it? Also, whats the name of the article, etc, maybe I can find it elsewhere. PAR (talk) 15:18, 15 September 2009 (UTC)

As stated in this article, the paper is "Length Contraction Paradox": Am. J. Phys., 29(6) June 1961. DonQuixote (talk) 11:31, 16 September 2009 (UTC)

Ok, the link you gave is working now, I have the paper. Do you have a copy of "The rod and hole paradox re-examined" by van Lintel and Gruber? Thanks PAR (talk) 18:14, 16 September 2009 (UTC)

That's irrelevant in the sense that it's about a practical application of rigidity and stress. Rindler's paper, at most, is about the "rigidity" of a mathematical line (hence the parabolic path) and not about a robust real-world application, although it uses real-world items to set up the problem. Note that his solution is "z'=etc", which is a mathematical line.

Actually, I took the time to do a flash animation yesterday which involves a row of rockets [2], and you'll see that, at the core, it's about relative simultaneity. DonQuixote (talk) 17:09, 17 September 2009 (UTC)

After reading the Rindler paper, I agree, the paradox should stay, it is a well defined and interesting problem. The crucial thing that was missing in the article and in my mind, was the fact that the man (or rod, or row of rockets) do not begin to experience force until they are all over the hole (in the hole IRF), at which point they simultaneously (in the hole IRF) experience a downward force. This is done with a "trap door" in the original paper, and with separate rocket engines on your animation. This is what is confusing the issue - the whole problem of force of the table or asphalt or whatever on the rockets is not an issue. It means that the possibility of tipping, etc is not an issue. The table or asphalt doesn't even need to be there, except to define the hole. I think that your rocket animation is far more informative than the present diagram, and you should replace the present diagram with some version of the animation. PAR (talk) 17:39, 17 September 2009 (UTC)

I would love to, but there's that time thing (I have to teach four classes this sememster). I'll try to figure out animated gifs and and such as I find time. Anyway, as for the "trap door" and such, I think that the section, as written now, is adequate as I geared it towards a general audience. If you want to expand it by stressing the simultaneity in the grate RF, then feel free to do so. DonQuixote (talk) 11:53, 18 September 2009 (UTC)

Recent criticism

The section "Recent criticism" contains a single primary source, whose arguments, as far as I know, are not accepted by the scientific community, so I removed it per WP:UNDUE and WP:SECONDARY. Anyone, who wants to include the article, should provide an independent and reputable secondary sources, which show that this paper is worth to be included. --D.H (talk) 23:28, 18 December 2010 (UTC)

The first paper is now represented by a book of the same author as the paper; that isn't an independent secondary source either. Moreover, the second paper is apparently accepted (appreciated and cited) by the scientific community. However, the disagreement between the two papers is about a detail that doesn't need to be discussed. Harald88 (talk) 15:22, 11 February 2012 (UTC)

PS I read again the policy concerning secondary sources, and it looks like it has been improved; in any case, your statement here above isn't valid now. Harald88 (talk) 17:23, 11 February 2012 (UTC)

The Rindler paradox (in it's original form) is cited in standard textbooks of relativity (such as Wheeler/Taylor). That the criticism in the second paper is notable (or even accepted) compared to the established textbook version, certainly needs a secondary source. GoogleScholar don't give much - for instance, I found those papers (arXiv:0809.1740, arXiv:0809.1721 published in AjP and EjP) which referred to it. --D.H (talk) 18:54, 11 February 2012 (UTC)

Again: that's not how the policy is formulated. Instead, secondary sources are needed to establish the topic's notability and to avoid novel interpretations of primary sources, but primary sources are permitted if used carefully. And as we appear to agree that we don't need to discuss the criticism, there isn't any issue here. Harald88 (talk) 19:02, 11 February 2012 (UTC)

Sorry, then it was a misunderstanding. I actually was referring to the discussion, not about listing the source in the references section (which is of course allowed since it was published). --D.H (talk) 19:16, 11 February 2012 (UTC)

OK, I was afraid that you intended starting an edit war. After reading your arguments, today I merely improved the notation of the reference and added a precision to the description, which I think was and remained in agreement with both papers. However, it appears that you do not appreciate the precision that is sourced from the second paper, and which is certainly not controversial but simply insightful. What is your beef with it? Harald88 (talk) 19:21, 11 February 2012 (UTC) PS: The second paper's precisions did already appear in an online physics book, but I think that in the new edition the whole paradox isn't mentioned anymore. Harald88 (talk) 19:24, 11 February 2012 (UTC)

As I said, this was a misunderstanding. But if you want my private opinion (that of course doesn't count): The "bottom-top-stiffness" argument can by avoided by mounting a large number of engines within the rod (from the bottom to top, and from front-end to back-end). They can be (almost) simultaneously activated in the grate frame by a strong magnetic field that propagates with light-speed from the grate. Those engines accelerate the rod in its entire vertical as well as horizontal extension into the grate (almost) simultaneously. However, in the rod's rest frame, only the engines in the vertical direction start (almost) simultaneously and bend the rod, while the horizontal ones follow afterwards in accordance with relativity of simultaneity. This is the essence of Rindler's paradox: If one somehow manages to let fall the rod in one frame (and this is always possible under certain assumptions), then it must fall in all other frames. --D.H (talk) 20:09, 11 February 2012 (UTC)

That is a different version of the paradox than the one described by Rindler. And what counts is our fair presentation of peer-reviewed, cited papers - our opinion is not allowed to play a role in our edits! Harald88 (talk) 20:50, 11 February 2012 (UTC)

Exactly, and this leads to the source-situation given above, but no need to repeat everything. --D.H (talk) 21:12, 11 February 2012 (UTC)

Also (and this too is a private opinion), the "bottom-top-stiffness" can be avoided by making the rod's thickness mono-atomic (which mathematically it is in the original paper since it only dealt with x/y coordinates and calculated a path). DonQuixote (talk) 20:40, 11 February 2012 (UTC)

That is again a different situation than the one by Rindler... and if you want my personal opinion, a mono-atomic rod will have a hard time to be of any significant stiffness at all. Harald88 (talk) 20:50, 11 February 2012 (UTC)

Lorentz aether theory...

Lets not forget that the "lenght contraction" concept was introduced by H. Lorentz to explain the negative result of the Michelson-Morley experiment, considering the existence of a completely motionless Aether. Probably we would not ecounter any paradox if we consider that the "lenght contraction " is a reaction on the moving bodies through the Aether. —Preceding unsigned comment added by 71.185.137.240 (talk) 01:52, 2 May 2011 (UTC)

Bar and ring paradox -- angle for both observers

I note that from the reference frame of the bar, the ring is moving at an angle. I wonder why this should not be true also in the other view. Shouldn't the bar be observered under an angle when in the reference frame of the ring? Koornti (talk) 13:04, 19 June 2011 (UTC)

No. Assuming both angles are the same is what causes the paradox in the first place. In the reference frame of the ring, the bar is parallel to the plane of the ring, and the only reason it fits through is because of the Lorentz contraction. If we make the wrong assumption that in the reference frame of the bar, the angle is the same (i.e. parallel), then the bar will not fit through the ring, because the ring is Lorentz contracted. If the ring and bar are rotated in the frame of the bar and we make your wrong assumption that the angle must be the same in the frame of the ring, then... well, then there is no paradox. They would fit through each other even if the speeds were slow.

Thanks. I was thinking of an opposite angle, but missed that it was a given that they are observed as parallel from the reference frame of the ring. Somehow thought of the two objects first being at rest in the same reference frame, parallel, far apart, and then the bar starting to move in one direction towards the ring... That was of course not the case. -- Koornti (talk) 15:44, 19 June 2011 (UTC)

Resolution??

After the paradox has been completely and correctly resolved, we have a section entitled, 'Resolution', which gives an unrealistic, unsourced, and in my opinion unhelpful, resolution of the paradox. Any comments?

I have no objection to giving a description of what would actually happen if you tried to carry out the experiment. It is rather more exciting that the current 'resolution'. Martin Hogbin (talk)

Based on currently available reliable sources, this is what happens. Thank you for your original research. Please publish it in a reliable source so that we can cite you. DonQuixote (talk) 13:44, 6 October 2013 (UTC)

Of course it is not what would actually happen if you carried out the actual experiment, and there is not a single reference to support the current text. It is that text which is OR. Martin Hogbin (talk) 17:00, 6 October 2013 (UTC)

I am the original author of that bit of text, and I have to admit that I paraphrased Rindler's original paper ("simultaneous acceleration of the rod" and "sequential acceleration of the rod") and applied it to the ladder ("simultaneous acceleration of the ladder" and "sequential acceleration of the ladder"...sorry, early days of Wikipedia). You can mark it with a {{citation needed}} tag if you wish. At the time, I was trying to summarize the text in Rindler's book Relativity: Special, General and Cosmological and his original length contraction paradox paper. DonQuixote (talk) 21:16, 6 October 2013 (UTC)

Let me explain the problems with it that I see:

Unrealistic material

The ladder in your example is tacitly assumed to be made of a particular brand of Unobtainium which neatly compresses under the forces and energies involved. The kinetic energy of a ladder travelling at, say, 1/2c is roughly similar to that released by the Tsar bomba. What actually happens is that, as soon as the front of the ladder touches the wall, a fireball of plasma and radiation rapidly propagates, destroying everything in its path. Rindler probably assumed that this point was understood by his audience, or maybe he was talking about a different setup.

Final outcome

Unlike the explanation above, your example only considers the case from the frame of the ladder, giving impression that in one frame the ladder compresses but, in the other, length contraction ensures that it neatly fits in the garage. Even with you special materials, the result in both cases is that latter ends up squashed. This important part of the resolution needs to be made clear; in both cases the rear front door of the garage can be closed before the entire apparatus is destroyed.

Relativity of simultaneity?

You give the reason for the limited speed of the compression effect (or fireball) as the relativity of simultaneity. This is not particularly relevant and makes the explanation harder to understand. The speed of the effect of the front contact is limited by the speed of light. In the realistic case the fireball front will be radiation travelling at the speed of light in both frames. This is a simpler and more accurate explanation. Martin Hogbin (talk) 08:44, 7 October 2013 (UTC)

Ok, the thing is that this isn't supposed to be that complicated. It's like using ideal gas or ideal fluid or ideal spring or frictionless surface. We can replace the ladder with a line of rockets, which would be more realistic, but the traditional example deals with a ladder (or pole). DonQuixote (talk) 12:22, 7 October 2013 (UTC)

Yes, I understand the idea of using a string of rockets but, if we do this in our minds I think we should do so in the article. Many readers will not appreciate that the latter could be idealised as a string of independent particles. If we do that though, we lose the benefit of the section, in that it is now similar to the explanation above.

I think some readers may want to know what would actually happen if this (impractical) experiment were really to take place. This raises some important aspects of the paradox. Firstly, we should show that the final outcome is the same for both frames. In the first explanation it is clear that the ladder passes through the garage in both cases without hitting the doors. When there is only one door it may look to some that the final outcome is different in the two frames.

Secondly it is worth showing that any event at the front of the ladder cannot have any effect at the rear of the ladder before the garage door is closed, even when the information is propagated at the speed of light, as is the case with the radiation from the front collision. Martin Hogbin (talk) 17:28, 7 October 2013 (UTC)

Feel free to copyedit the article, but please be careful to keep in mind Wikipedia's policy on original research while doing it. And thanks for taking the time to proofread this article. DonQuixote (talk) 23:29, 7 October 2013 (UTC)

Unfortunately, it is not copyediting that I think is required. Although you say that the current section is based on Rindler, you give no reference and therefore the section as it stands is OR.

I think the section should be deleted completely as it adds nothing to the resolution given above and is actually misleading in some respects. You have not responded to my detailed criticism. Martin Hogbin (talk) 08:48, 8 October 2013 (UTC)

I cited Rindler's original paper and copyedited so that the parts I cited matched his paper. The ladder is made out of the same material, as it were, as Rindler's rod. The important points from his paper are all parts of the object accelerate simultaneously in one frame, the object accelerates sequentially in the other frame, and the question of "rigidity". DonQuixote (talk) 11:21, 8 October 2013 (UTC)

The resolution still misses some essential points, for example, that the final outcome is the same in both frames. The article you have cited is about the related 'man walking over a grate' problem which we cover later on. Martin Hogbin (talk) 14:55, 8 October 2013 (UTC)

Feel free to edit the article. Be sure to edit any surrounding text if you remove bits. DonQuixote (talk) 15:28, 8 October 2013 (UTC)

Simultaneity resolution diagrams.

Why in the diagrams does the garage start with both doors open? Martin Hogbin (talk) 10:23, 6 October 2013 (UTC)

It's to simplify the illustration. Adding an additional step of opening the doors just adds more words. DonQuixote (talk) 13:43, 6 October 2013 (UTC)

You do not need to open both doors at the start. Only the front door need open initially. Martin Hogbin (talk) 17:01, 6 October 2013 (UTC)

Yes, that's true. But you don't need to have it closed either. It's just to simplify the illustration. That is, adding an initially closed door would be distracting. It's like illustrating the concept with two bulbs and starting with both of them off. Yes, you can start with one of them on, but that won't add anything to the illustration. DonQuixote (talk) 21:19, 6 October 2013 (UTC)

OK. Martin Hogbin (talk) 17:30, 7 October 2013 (UTC)

It is much clearer to start with the right door closed and left door open. That is because the essence of the paradox is: 1) why doesn't the ladder hit the closed right door? and 2) why doesn't the left door hit the ladder when closing? Starting with both doors open may contribute to the erroneous belief that some kind of acceleration is necessary to resolve the paradox. Lexchis (talk) 16:57, 3 January 2014 (UTC)

Relativity of simultaneity?

Watch closely figure 4 and 5 and tell me: if i'm the garage and I put a clock on each door that signs the time when they close in figure 4 they would have the same time (indeed they are in the same system of reference moving at the same speed=0). Now if you move on to figure 5 it seems that this is impossible, one door must close before even thought they still share the same system of reference (both moving at the same speed, same time and length correction applies). Which one happens? I mean, build the damn thing and let that ladder pass through the garage: now you have two timers that tell you a number, how is it that the same number cannot be moving in the ladder reference? Ok it can be different but not to each other!

To add some fun: in the experiment of Einstein about the train and lightning add also a clock near each area of the stroke so that also the time is shown (note that they are synchronized in the platform reference frame). Now the observer in M' sees B before A as usually (it happens too in classical mechanics for every speed indeed...) but it also sees the same information about time in each and it tells that the two events were simultaneous. Relativity what? I'm still so dubious :-/ 2.230.238.141 (talk) 15:42, 19 November 2013 (UTC)

From the garage's reference frame, both clocks will read the same time and the doors will close at the same time. From the ladder's reference frame, the clocks will appear to read different times but each will read the same given value when the doors close individually. DonQuixote (talk) 16:14, 19 November 2013 (UTC)

The thing you are missing is the initial synchronization of the clocks. In figure 4, they will only read the same time for the door closings if they both read zero at the same time. If you set both clocks to zero at the front door and move the second one to the back door, they won't be synchronized after you move it, due to time dilation during the movement of the second clock. So you would have to offset the second clock a little to account for that. That's one way to synchronize. Or you could put both clocks in place at the front and back door, and send, say, a light signal from the center of the garage, and they set to zero when they receive the light beam. That's another way to synchronize.

In figure 5, however, those same clocks won't be synchronized. The offset that you apply in the first scenario will not synchronize the clocks in the ladder frame, due to the motion of the garage. In the second scenario, the time it takes for the two beams to go from the center of the garage to the doors will not be equal, because the garage is moving, and again, the clocks will not be synchronized. They will give the same reading when the ladder enters and exits the garage, but they won't read zero simultaneously.

That's what is meant by "relativity of simultaneity". When you say that two clocks are synchronized (e.g. both read zero at the same time), but are separated in space, it only has meaning in a particular reference frame. Two spatially separated clocks synchronized in one frame will not be synchronized in any other frame that is moving with respect to the synchronized frame. PAR (talk) 05:32, 20 November 2013 (UTC)

Ok. As last question this particular ladder paradox, that in the worst of the cases breaks only causality of events for the observers: It's composed of a garage (two opposed doors, both open) and a ladder that have both a length of L at rest to each other, also garage height is 1/10^9 L (or any value very small compared to the length). No clocks or time devices of sort. So you accelerate the ladder along axis x from a large distance to the garage and stop to continue moving at constant speed. The experiment starts now: the speed of the ladder is such that it's length is about L/10 for the garage. When the tip of the ladder reaches one door (say left side for this example) a light signal is sent on the right so that it travels preceding the ladder. The door on the left closes only when all the ladder is passed, the fastest possible. On the right side the light signals arrives and the right door is immediately closed. Now the ladder is still travelling at constant speed inside the closed garage and without any undergoing acceleration, of course it will crush at some time on the right door but that's not the focus in this paradox.

The paradox itself is that the left door closed before the right one because it's closing caused the right one to do so. Ok I'll say it better: a sensor in the left door saw the tip of the ladder and sent the signal, while waiting for the ladder itself to pass so that it can also close the left door.

Numeric solution: ladder speed is 0.995c and Lorentz factor about 10, L is equal to 1 light-second (of course to simplify the results). In the garage reference when the ladder tip reaches the left door the light signal starts. It moves on to the right door (in 1s) and closes that one. The ladder in that time as almost reached the door but not touched it or received any acceleration/force whatsoever. The left side is more interesting: because the ladder length is 1/10 light second (contracted) it takes about 0.1s to pass. Then the door is closed and in a very short time: it's only 1/10^9 L!. So the ladder is in , travelling for about 0.9s before crashing, and you can for example take a nice picture of it from both sides of the garage. Or open again the right door before it crashes. But if you move on to the ladder reference it's impossible to do so: the garage is too small to fit! Or better: how can you close one or the other door in any sequence possible (and without touching the ladder?).

If the right one closes before then the ladder must impact it and contract to a shorter length before the left one can close, but the garage never touched the door (it can also open again before the crash indeed). If the left one closes before the ladder tip on the right is already passed out: but this is impossible because the light must travel faster than the ladder and close the right door before! Then they can close both at the same time, but this is still nonsense because it can't fit in any way. So? Thanks for any reply in advance and for answering me the previous doubts. Hope I didn't do anything too wrong ;-) 2.230.238.141 (talk) 16:08, 20 November 2013 (UTC)

Either the right door will open (see the double door example) or the ladder will accelerate into the reference frame of the garage (both the ideal acceleration example and the finite transmission of force example). In the latter, the front end of the ladder will accelerate before the rear end until, from the perspective of the rear end, the ladder is length contracted into the garage. DonQuixote (talk) 20:01, 20 November 2013 (UTC)

Don Quixote is right - you say "If the right one closes before then the ladder must impact it and contract to a shorter length before the left one can close, but the garage never touched the door (it can also open again before the crash indeed)"

In the ladder frame, if the right door closes, then the ladder will impact it, and it will contract to a shorter length before the left one closes. If it is open, then the right tip of the ladder passes through it. Later, the left tip of the ladder passes through the left door.

The ladder is never fully inside the garage in the ladder frame. "Being inside" means that the left and right tip of the ladder are simultaneously inside the garage, but since simultaneity is relative to the inertial frame and not absolute, "being inside" is also relative to the inertial frame and not absolute.

Taking pictures is a tricky business, because the light that comes into the camera from, say, the two ends of the ladder, may not have been emitted simultaneously, and so the picture will be distorted. If you take into account the speed of light, and relativity of simultaneity, you will find that the pictures predicted by both frames of reference will be identical.

I think you should learn to draw Minkowski diagrams. There is the intuitive notion of space and time (Galilean transformations) and then there is special relativistic notion of space and time (Lorentz transformations). You are mixing the two up and getting things confused. If you learn to draw Minkowsi diagrams, it all becomes clear, but it takes some time to learn. PAR (talk) 05:31, 21 November 2013 (UTC)

"thus the ladder can fit into the garage in both instances"

I have removed this final sentence from the intro. Strangely it seems to be several years old, but it's in direct contradiction to my knowledge of relativity and the article itself. The ladder does not fit in the garage in the second instance. — Preceding unsigned comment added by 81.151.71.121 (talk) 19:59, 16 February 2014 (UTC)

Thanks for the edit. You're right about it not fitting into the garage, but the tradition has been to make it fit in order to illustrate relative simultaneity (Rindler used the man falling in grate variation stubbing his toe against the grate to that effect). I've partially reverted and copyedited your addition to simplify the summary (the lead is supposed to be a simple, uncomplicated summary) because the full explanation of the thought experiment is in the article proper. DonQuixote (talk) 20:09, 16 February 2014 (UTC)

??? What do you mean, "make it fit by tradition". It's simply a physical fact that it does not fit! Just saying it does is... simply making an untrue statement. The rest of the article makes it explicit that in the second instance, the ladder cannot fit - which is correct. 81.151.71.121 (talk) 19:58, 17 February 2014 (UTC)

http://www.damtp.cam.ac.uk/user/tong/relativity/seven.pdf One of many citations I could give (and the article gives plenty of others). 81.151.71.121 (talk) 20:07, 17 February 2014 (UTC)

In the literature, the analysis doesn't just stop at length contraction. It goes further into relative simultaneity, non-simultaneous acceleration and finite speed of transmission of force. The lead is supposed to be a simple summary of the entire article. Any elaborations can be, and has been, mentioned in the article proper. DonQuixote (talk) 21:19, 17 February 2014 (UTC)

Two problem with this discussion are: Firstly it is not clear what 'fit into the garage' means. It might be better to reword this to make the resolution clearer. One possibility that I remember from the first time I heard this paradox is to say that the person rushes into the garage with the ladder and shuts the door behind him. In other words to fit the ladder in means that the door can be shut (before the whole setup is turned to plasma - see below).

The second problem is that both explanations do not mention what would actually happen in a real live case. Regardless of the frame of reference, the ladder, garage and runner are quickly turned to plasma by the energy released by the ladder hitting the garage. The kinetic energy of a ladder at c/2 is similar to that released by the Tzar bomba, the largest nuclear device ever exploded. Adding an element of reality can make the paradox resolution easier to understand. — Preceding unsigned comment added by Martin Hogbin (talk • contribs)

You're right, it should probably be worded better. In the literature, "fits into the garage" means that the door is shut behind him. Also, your second point is seldom mentioned in the literature. It would be great if someone would look into that and publish it (hopefully). DonQuixote (talk) 02:57, 18 February 2014 (UTC)

I am sure there are reliable sources somewhere that show would happen in reality, I will have a look. In any case it is pretty close to a routine calculation. The exact result may be complicated but two things are clear, firstly that the ladder carrier gets to close the door in either frame, and secondly that it always ends badly. Martin Hogbin (talk) 10:57, 18 February 2014 (UTC)

Far from being a "problem with the article", "real life cases" are utterly irrelevant. It's an idealised thought experiment! And the ladder doesn't hit the garage anyway, it just travels through it. Just look at the pictures?

More importantly, "fit into the garage" is very clearly defined. It means that both of the end points of the ladder are in the garage at the same time. In the first frame, this does occur. In the second frame, this does not occur. That is the entire point that this paradox is supposed to illustrate.

The ladder is never fully inside the garage in the second frame. This is a fact. There are multiple citations for it. I have explicitly added them to the article. The diagrams and explanation in the first part of the article also make this point clear. The introduction keeps being edited to state that the garage does fit in the garage in the second frame. Obviously this is a direct contradiction. Your protest that the introduction should be simple is bizarre - it does not validate inserting a "simpler" but completely erroneous statement which will confuse any poor student who happens across it. Without some kind of explanation, and without some kind of citation stating that the ladder fits in the garage in the second frame, there is no legitimate basis for these edits.

In the textbooks, the problem is described as getting both reference frames to have the ladder fit into the garage (the door closing behind the ladder) (Rindler, Wolfgang. Relativity: Special, General and Cosmological). This involves squeezing the ladder into the garage: simultaneously in the garage frame but sequentially in the ladder frame. And the intro should be simple because it shouldn't include the explanation in minute detail, that's what the article proper is for--so it's not bizarre, and it definitely isn't erroneous in the sense that the textbooks make it a point to squeeze the ladder into the garage. So the complete paradox isn't simply the different views from the reference frame but also includes the squeezing bit, at least in the published textbooks.

And thanks for your sources, but none of them are textbooks (see self-published sources), and until those get into textbooks, or even a peer-reviewed journal, the current, traditional description is good and doesn't need to be amended as yet. DonQuixote (talk) 13:35, 18 February 2014 (UTC)

As the article is currently written, your citation does not support your edits. The article refers to the standard presentation of the paradox where a rigid ladder travels at constant velocity v through a garage. Your citation refers to a completely different situation in which the ladder is decelerated inside the garage and elastically deforms. The intro does not talk about this thought experiment, and neither is it the subject of the main body of the article.81.151.71.121 (talk) 18:56, 18 February 2014 (UTC)

(EC)Er...as the original author of this article, I can state for a fact that I based it on Rindler's book and paper. The intro is about this thought experiment and the main body of the article is about this thought experiment as well. I don't know why you're having so much trouble understanding this. The "standard" version of the thought experiment, as has been pointed out above, involves the ladder being completely contained within the garage (or barn) with the door closed. DonQuixote (talk) 19:08, 18 February 2014 (UTC)

In addition I have reinstated citations 2 and 3, as they are written by physics professors and published by prestigious physics departments - "expert sources may be considered reliable when produced by an established expert on the subject matter, whose work in the relevant field has previously been published by reliable third-party publications." Blithely deleting these clearly valid sources is taking things too far. — Preceding unsigned comment added by 81.151.71.121 (talk) 19:03, 18 February 2014 (UTC)

All I have to say on this is that textbooks are unambiguously reliable sources, and therefore in my opinion trump blogs even if they're on university websites. Besides, they're addressing a completely different issue. As you have pointed out, these are about constant velocity. The traditional version of the ladder paradox has the ladder being squeezed into the garage. And as I have said above, I based the original version of this article on the textbooks which deal with the latter. DonQuixote (talk) 19:14, 18 February 2014 (UTC)

But the article and its introduction are about the far simpler and more common situation of whether a moving ladder fits inside a garage. The edit you keep making is not the correct edit for this article. It is for a different situation. Stating that it is also true in the situation presented in the article is false. The quality of your citation is irrelevant because your citation doesn't actually support your edit. 81.151.71.121 (talk) 19:50, 18 February 2014 (UTC)

Consider the admittedly unrealistic situation of a man carrying horizontally a 20-ft pole and wanting to get it into a 10-ft garage. He will run at speed v = 0.866c to make γ = 2, so that the pole contracts to 10 ft. It will be well to insist on having a sufficiently massive block of concrete at the back of the garage, so that there is no question of whether the pole finally stops in the inertial frame of the garage, or vice versa...The open 5-ft garage now comes towards the stationary pole. Because of the concrete block, it keeps on going even after the impact, taking the front end of the pole with it (see Fig. 3.1). But the back end of the pole is still at rest: it cannot yet ‘know’ that the front end has been struck, because of the finite speed of propagation of all signals. (Rindler)

So, no, you're wrong about the citation not supporting my edit. Again, the traditional description of the paradox involves the ladder (or pole) being "squeezed" into the garage. That is to say, the paradox describes a ladder within a garage from both frames and then offers an analysis where "whatever result we get by correct reasoning in any one inertial frame, must be true; in particular, it must be true when viewed from any other inertial frame. As long as the set of physical laws we are using is self-consistent and Lorentz-invariant, there must be an explanation of the result in every other inertial frame, although it may be quite a different explanation from that in the first frame." (Rindler)

Basically, this is what I'm seeing: the paradox involves a ladder that's inside of a closed garage in both frames. The traditional resolution to the paradox is that the ladder has to be accelerated into the reference frame of the garage, which allows the ladder to fit in the ladder's RF. What you're proposing is to say that there is no resolution to the paradox if the ladder is not accelerating. Well, yeah that's a given considering that the resolution is the ladder accelerating. DonQuixote (talk) 20:28, 18 February 2014 (UTC)

Your quote demonstrates precisely what I have been saying. Are you reading my comments..? The article describes a ladder moving with constant velocity. That textbook describes a ladder which is decelerated once inside the garage. Not the same thing. No, the ladder is not closed in the garage in both frames, just look at the diagrams in the first section of the article. In the ladder's frame it is never closed in the garage. 81.151.71.121 (talk) 20:39, 18 February 2014 (UTC)

Yes, the textbook describes a ladder which is decelerated once inside the garage, and so the this article--twice in fact. Please take the time to read the article and not just the lead. DonQuixote (talk) 20:45, 18 February 2014 (UTC)

Uhh... it was the lead which you kept editing. I know that later parts of the article addresses your alternate thought experiment. The lead and the main body of the article do not. They talk about the constant velocity version. Therefore the stated resolution should be the resolution for the constant velocity version. Not a different version. Obviously. 81.151.71.121 (talk) 21:04, 18 February 2014 (UTC)

The lead is a summary of the main body of the article...which mentions it twice. And no, the main body does not say that constant velocity is a prerequisite for the ladder paradox, so no, it's not about the "constant velocity version". The article is about the paradox as described in standard textbooks, as that's what I set out to write when I wrote the original version. (And thanks to the other editors who made this article better, by the way.) DonQuixote (talk) 21:11, 18 February 2014 (UTC)

I have to agree with the various anonymous, unsigned, and Martin Hogbin statements. If you define the ladder being "inside" the garage as having both ends simultaneously within the garage, then the ladder is never "inside" the garage in the second frame. The ladder is never physically "squeezed" into the garage in any frame. There may be a Lorentz contraction, but this is not physically "squeezing" the ladder. A distinction between the two must be made clear if the word "squeezing" is to be used. I think it should only be used for physical squeezing.

The statement in the introduction that "the ladder can made to fit into the closed garage in both instances" is simply false, and I have changed it. PAR (talk) 19:26, 18 February 2014 (UTC)

Yeah, the distinction should probably be made clear. And that line should probably be worded better. DonQuixote (talk) 20:28, 18 February 2014 (UTC)

Proposal For Slight Rewrite

There's clearly some confusion about exactly which thought experiment this article is supposed to be talking about. Currently I find the article rather confusing and messy, and probably quite unhelpful for the prospective reader.

Regardless of the history of the thought experiment, a quick browse of the internet and textbooks shows that it commonly refers to the simple situation where a long object like a ladder moves at velocity v unimpeded through some open structure like a garage. Considering the two different frames is what produces the paradox. The resolution, and the pedagogical value of the paradox, is that simultaneity is relative: the two ends of the ladder can simultaneously be in the barn in one frame, but not in another, and this is not a contradiction.

This should be the main subject of the article. It, and its solution, should be characterised in the introduction. The first section of the article should then describe in full the resolution. The pictures with the doors, and the Minkowski diagram, currently do a nice job of this.

Later sections can address any variations on the paradox which have some kind of substantive additional point. One of these is the variation where the ladder is stopped inside the garage and the doors shut, objectively "fitting" it into the barn. This is significantly more complicated and involves analysing the elastic deformation of the decelerating ladder. It would be a good addition, especially to emphasise that you can appeal to an unambiguous event in one frame to prove it occurs in any other, but it should not be the main focus of the article. Denziloe (talk) 20:12, 18 February 2014 (UTC)

I do not know which was the first version of this problem. The Rindler reference actually refers to a slightly different formulation of the problem. In the two-door version as shown here there really is not much of a paradox. In the frame of the barn, the ladder is contracted so that it fits into the garage. In the frame of the ladder the barn is contracted so, at no time, is the ladder wholly contained within the barn. That is exactly what most people would expect, so there is not much of a paradox. The paradox is actually, 'Why does the ladder not hit the doors?', which, in the frame of the barn, open simultaneously.

The far more dramatic version of the problem has a garage with only one set of doors. The person rushes into the garage and closes the door behind them. In the garage frame this is easy to understand, the ladder contracts, but how can this happen in the ladder frame? That is a real paradox. Of course, the resolution is similar to that of the the two-door version.

My suggestion is that we start the article with the one-door version of the problem, where the paradox is clear for all to see, and use the two-door version as a explanatory vehicle. Martin Hogbin (talk) 10:09, 19 February 2014 (UTC)

Just a comment, when I first wrote this article, I started with the one-door version and then put in a section before that explaining the concept of relative simultaneity to set up the resolution. I don't mind if the order is changed. I don't mind a complete rewrite either. DonQuixote (talk) 13:07, 19 February 2014 (UTC)

As I understand it, the purpose of this gedanken experiment is to show a situation where special relativity at first sight appears to be inconsistent in that it predicts different outcomes that depend on the frame from which the experiment is viewed. The resolution shows that the theory does in fact produce the same outcome in both frames.

I therefore think that it would be best to start with the version that appears most wrong at first sight. In the one-door version, it is simple to see how length contraction will allow a person to carry a 20 foot (rest length) ladder rapidly into a 10 foot room and shut the door behind them when viewed from the frame of the room. (People generally ignore what happens next). From the frame of the ladder, however, the ladder is 20 feet long and the room only 5 feet. At first sight it therefore seems absurd that person can still enter the room with the ladder and shut the door behind them. The resolution relies on the maximum speed at which energy and information can travel and also the relativity of simultaneity.

In my opinion the two-door version is not so dramatic but helps make clear how the RoS works. In a way it might be considered the first stage in the resolution of the one-door paradox. Martin Hogbin (talk) 14:33, 19 February 2014 (UTC)

I very much disagree that the constant velocity version is not a paradox. By reasoning in two different ways, one can obtain two conclusions; "the ladder fits inside the barn", and, "the ladder does not fit inside the barn". This is the very definition of a contradiction, and is very bemusing to the uninitiated. It requires a substantive analysis - namely analysing what exactly it means to fit a ladder inside a barn, which involves thinking about the relativity of simultaneity - to realise why this is still a consistent situation in SR. This analysis is the main pedagogical value of the thought experiment, and as I said, a brief scan of the literature shows that this is the most common presentation. It has the additional advantage of being simpler, not requiring any discussion of decelerating frames or the deformations of solid bodies; therefore it makes sense to put it first, and discuss more elaborate variations afterwards. Denziloe (talk) 14:44, 19 February 2014 (UTC)

The one-door version does not require not any discussion of decelerating frames or the deformations of solid bodies, only the fundamental principles of SR, the RoS and the maximum speed at which energy or information can travel.

It involves an instantaneous deceleration of the ladder from v to 0, and the ladder squeezes in its frame by virtue of it not being a rigid object. My main point is that it's clearly an additional level of complication. Denziloe (talk) 17:53, 19 February 2014 (UTC)

I do not understand what you mean by 'analysing what exactly it means to fit a ladder inside a barn'. In the frame of the ladder it does not fit in the barn. Martin Hogbin (talk) 16:01, 19 February 2014 (UTC)

The naive, classical view is that "X fits inside Y" is an objective relation. So "X fits inside Y" and "X does not fit inside Y" seems to be a contradiction. We have to be more precise about what "X fitting inside Y" means in terms of space and time. Denziloe (talk) 17:53, 19 February 2014 (UTC)

What do you think it does mean to say that 'the ladder fits in the barn'. Martin Hogbin (talk) 14:02, 20 February 2014 (UTC)

Current wording does not properly describe the experiment

The current wording talks about fitting the ladder in the garage. In the frame of the ladder it clearly does not fit inside the garage. In this version of the paradox it is the closing of the doors that is the issue. I therefore propose the wording below.

The simplest version of the problem involves a garage, with a front and back door, and a ladder which is too long to fit inside, when both are at rest with respect to one another. In the reference frame of the garage, the ladder passed at a high horizontal velocity, through the stationary garage. The doors are both initially open but both simultaneously close briefly when the is inside the garage. The doors then simultaneously both open to allow the ladder to continue through the garage. Because of its high velocity, the ladder undergoes the relativistic effect of length contraction, and becomes significantly shorter. As a result, as the ladder passed through the garage, and it was possible to close both doors simultaneously without hitting the ladder.

In the reference frame of the ladder, the garage which is moving with high velocity. It is therefore the garage which is length contracted and not the ladder thus the garage is far too small to ever fully contain the ladder and therefore it is not possible for both doors to simultaneously shut whilst the ladder is within the garage without hitting the ladder.

Could you give some detail as to what your exact issue is? The current article does make it clear that the ladder does indeed not fit in the frame of the ladder.

The proposed edit also has quite a few spelling and grammatical problems.81.151.71.121 (talk) 17:23, 20 February 2014 (UTC)

Improvements in wording are always welcome.

I presume you mean that the current article makes clear that, in the frame of the ladder, the ladder does not fit in the garage.

The problem with the current wording is that it does not make the intended paradox clear. Without the doors, in on frame the ladder is shorter than the garage and fits in it but in the other frame it is longer than the garage and does not. There is nothing paradoxical about that, it is exactly what would be expected.

The problem only comes when we try to shut the doors without hitting the ladder. Martin Hogbin (talk) 17:40, 20 February 2014 (UTC)

With the mistaken paradigm of absolute time, it is a paradox that the ladder fits in the garage, but also does not fit in the garage. The resolution is a discussion of the relativity of simultaneity. You need to approach this with the mindset of somebody who does not understand relativity. Obviously for anybody with a thorough grasp of relativity, none of these things are paradoxes. 81.151.71.121 (talk) 18:25, 20 February 2014 (UTC)

Resolution of what? There is nothing to resolve. In one frame the ladder is shorter than the garage, in the other the ladder is longer than the garage.

The purpose of this gedanken experiment is to create a case where the final outcome appears to depend on the chosen reference frame. In one case the garage doors can be closed without hitting the ladder but in the other case it appears that they cannot. That is what the left and right pictures show. Now we do need to use the RoS to explain why the closing doors do not hit the ladder in the ladder frame. Here are some refs which show that it is the closing of the doors that is the important point: [[3]], [[4]], [[5]]

I get the feeling you're just ignoring my replies. I've already explained what requires resolution, and so does the article. Your citations do not support your claims, and one of them is based on this Wikipedia article!!

What you are describing as a difference is just semantics. "We think the doors will collide with the ladder in the second frame" is exactly the same statement as "we think the ladder will not fit in the garage in the second frame". They are both paradoxical for exactly the same reason, and are resolved in exactly the same way. If you really want I will write some kind of reference to the doors in the second paragraph of the Paradox section, but this part of the article doesn't require any major edits. 81.151.71.121 (talk) 23:22, 20 February 2014 (UTC)

Please read the references that I gave you more carefully. "We think the doors will collide with the ladder in the second frame" is not same statement as "we think the ladder will not fit in the garage in the second frame". This is quite obvious from the fact that, in the ladder frame, the ladder quite obviously will not fit within the garage, but the doors do not hit the ladder. Martin Hogbin (talk) 00:13, 21 February 2014 (UTC)

You do understand why you can't use a Wikipedia article as a citation for that very same Wikipedia article, right..? Anyway, your other two links were fine but I still don't know what distinction you were trying to make. You just conflated "the doors do not hit the ladder" with "we think the doors do not hit the ladder". These are not the same. What we think will happen is obviously not the same as what will actually happen, or there would be no paradoxes. If we do not think the doors will hit the ladder, what exactly are you saying is the paradox? A paradox must involve two statements of the form "X" and "not X", so that there is a seeming contradiction.

What change are you saying needs to be made to the article? 81.151.71.121 (talk) 12:04, 21 February 2014 (UTC)

There is nothing particularly paradoxical about the fact that "the ladder will not fit in the garage in the ladder frame", it is just one of those surprising things that is common to SR. If, on the other hand, the doors collide with the ladder, the whole experiment will be engulfed in a plasma fireball. So if the doors collide with the ladder in one frame but not in the other that means that, when the experiment when considered in one inertial frame, the ladder passes freely through the garage but, when the same experiment is considered in another inertial frame, the whole experiment is turned to plasma. That is what you call a paradox. Martin Hogbin (talk) 21:30, 21 February 2014 (UTC)

Like I have said, if we presume absolute time - which we must to see any kind of paradox, involving doors or no - then it is a paradox, for the same reason that it's a paradox when you consider the doors: events happen in one frame but not in another. The events may be less dramatic but that's of no material consequence. It cannot be the case that the ladder is shorter than the barn in one frame but not in the other, because this means that, for instance, when the front of the ladder is at the exit of the garage, in the frame of the garage, the back end of the ladder is an event inside the barn, whereas in the frame of the garage, the back end of the ladder is an event outside the barn. An event can't have two different spacial locations. The doors are mainly a pedagogical tool to make the problem more vivid. You can find many treatments of the paradox with no reference to any doors, for instance [[[6]]].

Again, what exactly is wrong with the article..? It makes an additional reference to the doors now. I don't see how the paradox is not clear. 81.151.71.121 (talk) 10:47, 22 February 2014 (UTC)

No, there is no paradox in the version as it is now. It is somewhat unintuitive that each frame measures objects in the other frame to have contracted and this is indeed related to the RoS but there is no need for ladders, garages, or doors to discuss this. To rods would do the trick.

The point about the ladder paradox is that it appears that two entirely different outcomes occur, depending which frame you consider the same experiment from. This is patently absurd, even for relativity. Martin Hogbin (talk) 15:06, 22 February 2014 (UTC)

See previous comment. 81.151.71.121 (talk) 20:36, 22 February 2014 (UTC)

You previous comment does not explain how a well known fact about SR can be considered as a paradox and why it needs a garage and a ladder; nothing is made more vivid by them. The objective of this experiment is to show a case where it appears that the outcome depends in the reference frame. Martin Hogbin (talk) 17:59, 23 February 2014 (UTC)

The comment clearly addresses your question. When the front of the ladder hits the exit door, the back of the ladder can't be inside and outside the garage at the same time, even in SR. 81.151.71.121 (talk) 23:45, 23 February 2014 (UTC)

I see a lot of mis-statements:

" events happen in one frame but not in another" - no, an event happens in any frame.

You're conflating. As I made clear, this is referring to the paradox, where we assume absolute simultaneity. Of course an event happens in any frame when you do SR correctly, but the article has to present SR incorrectly in order to describe the paradox. 81.151.71.121 (talk) 14:14, 24 February 2014 (UTC)

" It cannot be the case that the ladder is shorter than the barn in one frame but not in the other, because this means that, for instance, when the front of the ladder is at the exit of the garage, in the frame of the garage, the back end of the ladder is an event inside the barn, whereas in the frame of the garage, the back end of the ladder is an event outside the barn. An event can't have two different spacial locations."

Yes, an event can have two different spatial locations, only its space-time location is fixed. Spatial location is dependent on the reference frame.

Again, if you read the comment, we've presumed absolute time. So it's referring to two different space-time locations for the same event. One event cannot be inside and outside the garage, not even in different frames in SR. 81.151.71.121 (talk) 14:14, 24 February 2014 (UTC)

"When the front of the ladder hits the exit door, the back of the ladder can't be inside and outside the garage at the same time, even in SR"

Yes it can. "Same time" is different for different inertial frames.

Again, if you'd read the comments... you're just describing the resolution to the paradox. Everybody here understands SR and the basics of this article quite well, thank you. Obviously we can't talk about relative simultaneity this when describing the paradox, or there would be no paradox. 81.151.71.121 (talk) 14:14, 24 February 2014 (UTC)

The ladder paradox is basically a clarification of the Lorentz contraction. There is no physical squeezing of the ladder. The length of the ladder is the distance between the locations of its end points, those locations being measured simultaneously. Since simultaneous in one frame is not simultaneous in another, the length in one frame is not the same as in the other.

Which is what the article says. 81.151.71.121 (talk) 14:14, 24 February 2014 (UTC)

The two doors clarify things, make the paradox much more obvious. If you make the error of assuming that simultaneity is absolute, then there is a paradox. Slamming both doors shut simultaneously when the shortened ladder is in the garage makes it clear that the ladder is contained in the garage when in the garage frame. Going to the ladder frame, it is clear that the ladder can never be contained in the garage in that frame. Only when it is clear that the two doors do not close simultaneously in the ladder frame can it be clear that the paradox is resolved. PAR (talk) 05:54, 24 February 2014 (UTC)

Thanks for your interest, your opinion on what the ladder paradox is all about would be most welcome. I certainly do understand the subject and the points you make. Here is my point:

The ladder (or pole and barn) paradox is intended to produce an obviously absurd situation if the RoS is not taken into account. The idea is that, at first sight it seems that, when viewed in the garage frame, the doors can shut without hitting the ladder but, in the ladder frame, the doors will hit the ladder, with disastrous consequences. This leads to an absurd conclusion which is that, when viewed in the garage frame, the ladder passes through the garage unharmed but, in the ladder frame, the whole experiment is destroyed by the ladder hitting the doors. That is a real paradox. It is reslolved, as we know, by the fact that, in the ladder frame, the doors open sequentially. Martin Hogbin (talk) 10:46, 24 February 2014 (UTC)

So the statement "When the front of the ladder hits the exit door, the back of the ladder can't be inside and outside the garage at the same time, even in SR" should read "When the front of the ladder hits the exit door, the back of the ladder can't be inside and outside the garage at the same time, even in (incorrect) SR". This discussion is very confusing. The bottom line is, is the article, in your opinion, ok as is? PAR (talk) 06:23, 26 February 2014 (UTC)

In no model of physics can the location of an event be relative. This is the formal reason that a ladder fitting and not fitting in a barn in absolute time is indeed contradictory. In SR, "incorrect SR", whatever; if an event occurs in the garage in one frame, it must occur in the garage in any frame. This notion is correct, and essentially it's what drives the paradox. Objecting to the ladder fitting in the garage but also not fitting in the garage, under the assumption of absolute time, is indeed a valid objection. It's just that the assumption of absolute time is not a correct one. Clarifying this is the purpose of the thought experiment. Denziloe (talk) 12:14, 26 February 2014 (UTC)

No, the article is vary far from being OK in my opinion because it fails to present the essential paradox at all. That two observers in relatively moving reference frames both measure objects in the other frame to be contracted is indeed somewhat unintuitive and unnatural but to most people it is believable. Just to demonstrate that fact does not require a ladder fitting into a garage.

What this gedanken experiment is intended to do is to create a situation that, at first sight, produces an absurd conclusion, which is that, when considered in one reference frame, the ladder passes unharmed through the garage but, when considered in another reference frame, the ladder hits the doors and the whole experiment is turned to plasma. That is what makes a (veridical) paradox; something that at first sight appears utterly absurd but which, on careful consideration, is shown to be logical. Martin Hogbin (talk) 08:56, 26 February 2014 (UTC)

Firstly, the article has already been accommodated to your tastes. In addition to presenting it as paradoxical without the doors, to drive home the point as you requested, the article already makes an additional reference to the ladder hitting the doors in the second frame but not the first. You've been asked a number of times what you actually think is wrong with the article that has actually been written, but so far you haven't given any answer. So I'm really not clear what your specific problem with the article is. The issue, which are you arguing is a flaw, is not even a feature of the article in the first place.

Secondly, although to a naive student there is nothing inherently contradictory about length contraction in conjunction with a paradigm of absolute time, the whole purpose of the paradox is to show, by considering a special circumstance, that there actually is a contradiction. If you think about it, this is the case with pretty much any physical paradox. The fact that length contraction in absolute time seemed believable before seeing the paradox isn't an argument against the paradox.

Once the paradox has been presented, it becomes clear that there is a problem; most students would instantly find something contradictory about an object which fits and doesn't fit in a garage at the same time, and they are indeed correct to do so. If this isn't enough, the problem is brought into even sharper focus by considering the doors of the barn, as you recommended. Denziloe (talk) 12:14, 26 February 2014 (UTC)

My taste does not come in to it. The whole point of the paradox is to show what seems like a dramatic difference two outcomes for the same experiment [this source] says, 'Well does the pole get caught in the door or doesn't it? You can't have it both ways', and [this source] (which simply mentions WP, the author clearly has his own opinion on the subject) says, 'How on earth is the ladder supposed to make it through the garage in this reference frame?'. [Here] we have, 'I hope the far door is open!!'.

Now please explain to me what is paradoxical about the fact that, in one frame the ladder is longer than the garage but, in the other frame the garage is longer than the ladder. This is exactly what someone who has just been introduced to Lorentz contraction would expect. Martin Hogbin (talk) 15:47, 26 February 2014 (UTC)

Someone just introduced to the Lorentz contraction would say that is a paradox, made concrete by the ladder paradox. The idea that two observers in relatively moving reference frames both measure objects in the other frame to be contracted is NOT "believable to most people", and constitutes a paradox under the assumption of absolute time. That paradox is, for example, the ladder paradox. The doors make the paradox even more concrete. The garage is not an "event", but the closing of the doors are events, and serve to make concrete the idea that the ladder is or is not inside the garage. PAR (talk) 16:33, 26 February 2014 (UTC)

Martin, I've already given a citation demonstrating that the doors are not essential to the paradox, but rather, as PAR says, complimentary to the paradox. For the third or fourth time: this is already how the article is written. I agree with you that reference to the doors is helpful, and the article reflects that. You have repeatedly declined to explain what you think is actually wrong with the article. I do not understand your behaviour.

I've also already explained why the situation without the doors is already paradoxical. To repeat: if the ladder both fits and does not fit in the garage, then, when viewing the situation with the assumption of absolute time, there are times, for instance when the front of the ladder is near the exit of the garage, when the back of the ladder is both inside and outside the garage. This is intuitively absurd, and this intuition is correct, for it is indeed illegal in special relativity. So the intuitive rejection of a ladder both fitting and not fitting inside the garage is valid. In case a student does not have this intuition, reference to the doors further clarifies why the situation is untenable. Denziloe (talk) 13:45, 1 March 2014 (UTC)

How Does The Ladder Actually Reach Its Velocity?

Naively we might want to apply a simultaneous force to each part of the ladder so that it accelerates uniformly - if we just apply a force to one part of the ladder, it will deform due to the force transmission being bounded by c.

This would bring it to a high velocity, as the article requests.

But, in the frame of the garage, the two ends of the ladder have had identical velocities the whole time, and so the distance between them is unchanged; the ladder is not contracted, and it does not fit in the barn.

How is this resolved? 81.151.71.121 (talk) 15:39, 23 February 2014 (UTC)

That is a very good question, which is resolved here. Martin Hogbin (talk) 10:51, 24 February 2014 (UTC)

Thanks! How could we phrase the article to make this detail clear? 81.151.71.121 (talk) 14:05, 24 February 2014 (UTC)

That is a subject in itself and details such as that are normally ignored in gedanken experiments like this. As I say below, it does not really matter how the ladder is accelerated so long as it is not damaged and is allowed to assume its natural length once it is travelling at constant velocity. Martin Hogbin (talk) 17:43, 24 February 2014 (UTC)

It's a thought experiment. It starts in that IRF. DonQuixote (talk) 16:46, 23 February 2014 (UTC)

The article currently doesn't make that clear, though. It just says that the ladder is made to move at the velocity. 81.151.71.121 (talk) 17:24, 23 February 2014 (UTC)

It does not really matter so long as the ladder is not damaged. It is allowed to assume its natural length once it is travelling at constant velocity. Martin Hogbin (talk) 17:52, 23 February 2014 (UTC)

Archive 1