Talk:LC circuit/Archive 1

Archive 1

Series and Parallel circuits

The present page only covers a parallel tuned cicuit and is therfore not complete. It should also include a series tuned circuit as these also come under the title "LC circuit(s)". Light current 04:45, 2 August 2005 (UTC)

Indeed, the article should also contain information about series LC circuits. In its current condition it's quite different from the articles for RC_circuit and RL_circuit. Pink-isnt-well 17:04, 23 September 2006 (UTC)

in my point of view the picture should have a load in one side and an AC input signal in the other side and the author should emphasizes that in the resonance freq. the current output toward the load is zero. —Preceding unsigned comment added by 216.31.211.11 (talk) 02:38, 31 January 2009 (UTC)

Basic info

One thing this article doesn't say is... what does "LC" stand for? GAH! --tgeller 17:11, 9 August 2006 (UTC)

L and C are the common symbols for inductance (inductors) and capacitance (capacitors), respectively. ~MDD4696 16:44, 14 August 2006 (UTC)

Almost information free

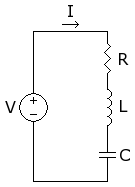
I'm sure that everything in this article is meaningful and informative to students of Electrical Engineering, but it is lacking a great deal in terms of communication to the young inquiring mind or to the general public. Consider the first diagram,

LC circuit diagram

. It shows a loop with a only an inductor and a capacitor. The article claims it resonates. No antenna, no voltage source, no power source, no current source: it seems unlikely. Perhaps with superconductors?

It seems to me that the entire present article should be pushed down a ways into some sort of "technical depictions" area, and a more open discussion of the topic should precede it. Supposing I had a capacitor and an inductor and a battery (and I do have all these things) what I want to learn is: how can I hook them up to form an LC, and how will it behave? I can look up what an inductor or a capacitor is and does, but I have no real sense of what it means to say that the current alternates between them. From the diagram or with them in series, I'd think it was impossible for there to be more current in one than the other (unless the frequency is incredible).

As an example, suppose we draw a circuit with a voltage differential applied across the I&C in parallel. A simple text description of the result would be tremendously illuminating: the circuit will resonate at a frequency defined by (equation), where by "resonate" we mean that current from the voltage source will vary as (picture of waveforms). As voltage is increased,...,as current increases,.... I don't know what a "current source" means in practical terms absent voltage. I suppose a battery is a current source to a short circuit and a voltage source to an open circuit? I don't think any general discussion should make use of the truly ideal concepts without any concrete representation (if that's what a current source is). Does the circuit even do anything when constant voltage is applied?

wikifiyied oscillator for you. I am planning to draw some images about how to add damping, driving, leaking.Arnero 11:53, 18 November 2006 (UTC)

History

Invented by William Thomson, 1st Baron Kelvin ? Arnero 16:47, 18 November 2006 (UTC)

"The first patent for a radio system that allowed tuning was filed by Lodge in 1897, although the first practical systems were invented in 1900 by Italian radio pioneer Guglielmo Marconi." Marconi is not the inventor of the radio. Tesla is not mentioned at all in this article, but his work with resonance was arguably the most important development in radio engineering. And he actually did invent the radio. 81.159.29.158 (talk) 15:57, 25 July 2013 (UTC)

Impedance of Series/Parallel LC circuits

It states under the the Series LC circuit section that it "act[s] as a band-stop filter having infinite impedance at the resonant frequency of the LC circuit."

I am no expert but when plug the numbers into the equation I get 0 impedance at the resonant frequency, making it a band-pass filter.

The opposite is true for the Parellel LC circuit description as well. It states that "the parallel connected circuit will act as band-pass filter having zero impedance at the resonant frequency of the LC circuit." Plugging the numbers in again, at the resonant frequency the impedance is infinite making this a band-stop filter. —The preceding unsigned comment was added by Charlesthomasbarnes (talk • contribs) 17:48, 17 January 2007 (UTC).

Intro

I stopped by for some reference material for a friend who needs help teaching electronics. I changed "tune circuit" to the conventional term of "tuned circuit". I see it was previously changed the other way. I also improved the next sentence because current can flow at any frequency, not just resonance.

In view of some older comments, I also think it appropriate to add something at the end of the Intro such as: "While no practical circuit is without losses, it is instructive, nonetheless, to study this pure form to gain a good understanding." COMMENTS?

-- Steve -- (talk) 20:29, 7 December 2010 (UTC) EngineerSteve

I think that the word "practical" is misleading, and entirely removing it from that sentence would improve the accuracy of what you're trying to say. Spiral5800 (talk) 15:38, 26 March 2011 (UTC)

Revealing the truth about electrical resonance phenomenon

I have copied the text below from Electrical resonance talk page. Please, discuss. Circuit dreamer (talk, contribs, email) 22:17, 21 July 2011 (UTC)

Bless my soul! I know it looks strange and incredibly, and probably you will not believe me... but I have finally revealed the secret of the ubiquitous electrical resonance phenomenon! It is interesting that the negative impedance phenomenon has helped me to find out credible intuitive explanations about the impedances of series and parallel LC circuits. I would like first to share my insights with you here; then to compress these lengthy explanations into a few sentences and to place them in the main article...

Realizing the LC arrangement

The fault of the classic formal approach when explaining the zero and infinite impedance of series and parallel AC-supplied LC circuits is that it implies two dual impedances (inductive and capacitive) that cancel each other thus giving total zero or infinite LC impedance. But this widespread assertion is misleading...

It is hard for people to imagine how two humble impedances can cancel each other as "impedance" gives an impression of something passive. Two passive "things" shouldn't cancel each other; one of them should be active (a source). So, we have to consider an LC circuit as a combination of two elements: a source (active element) driving a load (passive element). Depending on the situation, the either element (the inductor or capacitor) can act as a source; meantime, the other element will act as a load. Strictly speaking, both they are sources containing energy (magnetic or electric); but figuratively speaking, the load is a source that is "forced" to act as a load (like a charging accumulator). They can be distinguished by the signs of the current through and the voltage across them - in the source they are different while in the load they are equal.

Why the impedance of a series LC circuit is zero

We have an arrangement consisting of four elements connected in series: an AC input voltage source, an inductor, a capacitor and a load (a resistor). Or, we may combine the input voltage source and the resistor into a real voltage source (with internal resistance).

The main article says: "Inductive reactance magnitudeX_L increases as frequency increases while capacitive reactance magnitude X_C decreases with the increase in frequency. At a particular frequency these two reactances are equal in magnitude but opposite in sign; so X_L and X_C cancel each other out. The only opposition to a current is coil resistance. Hence in series resonance the current is maximum at resonant frequency". Let's now try to comprehend this magic...

According to the considerations about LC arrangement above, we can think of the series LC circuit as of an AC source and impedance connected in series. At the resonant frequency, this "source" has the same polarity as the input source; the two AC voltages are in phase with each other so they add together. Let's for concreteness consider the voltage polarities travelling along the loop at both the half waves.

Positive input half wave (travelling clockwise): -V_IN+ (source), +V_LOAD- (impedance), -V_L+ (source), +V_C- (impedance). The charged inductor acts as a source that "helps" the input source. Note the voltage across the inductor (the source) is equal to the voltage drop across the capacitor (the impedance) so the total voltage across the series LC circuit is zero. Its total impedance is zero and it does not impede the current. Very interesting... as though the inductor acts as a negative capacitor or as the output part of the op-amp in an inverting integrator that neutralize the capacitor impedance! Well, there is still a subtle difference:) The true negative capacitor and the op-amp use additional external energy (a power supply) for this purpose while this "negative capacitor" draws energy from the input source.

Negative input half wave (travelling counterclockwise): -V_IN+ (source), -V_C+ (source), +V_L- (impedance), +V_LOAD- (impedance). Now the charged capacitor acts as a source "helping" the input source. The voltage across the capacitor (the source) is equal to the voltage drop across the inductor (the impedance) so the total voltage across the series LC circuit is zero again; its total impedance is zero and it does not impede the current again. Now as though the capacitor acts as a negative inductor that neutralizes the inductor impedance!

We can generalize the two cases by one conclusion: An AC supplied series LC circuit consists of two elements connected in series and having equal voltages across them; one of the elements acts as a voltage source while the other acts as impedance.

It is interesting fact that from this negative impedance viewpoint, both the reactive elements can have negative impedance in this sense. They change alternatively their roles: once the inductor acts as a negative impedance element, then the capacitor does the same and so on, and so forth...

Why the impedance of a parallel LC circuit is infinite

Now we have a simpler arrangement consisting of two elements: an AC input voltage source driving an LC tank.

The main article says: "Let R be the internal resistance of the coil. When X_L equals X_C, the reactive branch currents are equal and opposite. Hence they cancel out each other to give minimum current in the main line. Since total current is minimum, in this state the total impedance is maximum."

To comprehend this assertion as above, we can now think of the parallel LC circuit as of an AC "helping" source and impedance connected in parallel. At the resonant frequency, the "source" provides all the current needed for charging the impedance to the input voltage; so there is no need the input source to do this donkey work:) The helping "source" as though acts as a load canceller (i.e., as a negative impedance again)! Actually, this arrangement is similar to the exotic bootstrapping technique: a voltage "source" (i.e., the LC tank) is connected in opposite direction to the input voltage source; as a result, the current is almost zero and the impedance is infinite. Of course, there is a subtle difference again:)

Circuit dreamer (talk, contribs, email) 22:12, 21 July 2011 (UTC)

So how does it really work ?

The explanations of how the impedance varies makes sense for these hypothetical circuits. And it says this is important for making a radio receiver work. It could really use some explanation of HOW this can make a radio receiver work, which remains unclear.Eregli bob (talk) 16:14, 9 January 2013 (UTC)

Capacitive reactance

@Akld guy: I've reverted your revert of the IP. The article defines $X_{C}$ as a magnitude. It is therefore always a positive quantity. If you want to make the sign of $X_{C}$ negative, you will need to change the definition as well. Having $X_{C}$ positive is commonly done in the literature (although not consistently by everybody). Capacitive impedance is then $-jX_{C}$, not $jX_{C}$. Likewise, the total reactance of a series LC circuit is calculated as,

$X=X_{L}-X_{C}$

or, for a parallel circuit, the same is done for susceptances

${1 \over X}={1 \over X_{L}}-{1 \over X_{C}}$

I don't mind which convention the article uses, but it needs to be consistent throughout with clear definitions. SpinningSpark 11:25, 9 January 2019 (UTC)

Yes, the article defines $X_{C}$ as a magnitude but there is no explanation of what the immediately preceding sentence means:

"At one particular frequency, these two reactances are equal in magnitude but opposite in sign; that frequency is called the resonant frequency f₀ for the given circuit."

Hence, at resonance:

${\begin{aligned}X_{L}&=X_{C}\end{aligned}}$

The reader may well ask, what significance does opposite in sign have. It's not explained, either in this section or any of the preceding. This needs explanation. Akld guy (talk) 20:36, 9 January 2019 (UTC)

Yeah, either that has to be changed to the impedance is opposite in sign, or else stop treating reactance as a magnitude. SpinningSpark 21:24, 9 January 2019 (UTC)

Direction of current flow not needed

@Chetvorno: Adding the direction of current flow, as in the sentence: If an inductor is connected across a charged capacitor, current will start to flow from the positively charged capacitor plate to the negatively charged plate through the inductor, is not only superfluous but misleading. You claim that it aids the uninformed reader for whom the page is written. Nowhere is it stated that this is conventional current flow direction. Therefore it might mislead the reader into assuming that this is a special case where the current flows in a particular direction because it's an LC circuit. If it's unnecessary, then let's not mention it. The reader can understand that current flows, he or she does not need to be told a direction that implies a special case. Akld guy (talk) 10:29, 3 October 2019 (UTC)

I think the convention is that conventional current is assumed unless stated otherwise. For a reader that does not know about current conventions, they are hardly likely to become confused about which one is being used, and for those skilled in the art, it will be obvious. On the substantive issue, I think Chetvorno is right that it is helpful to explain that the current through the inductor is being driven by the charge on the capacitor. That's not to say that a better form of words couldn't be found, but I think it is right to put something in. SpinningSpark 15:27, 3 October 2019 (UTC)

My objection is not to the fact that current through the inductor is being driven by the charge on the capacitor. Perhaps I gave that impression by quoting the entire sentence. No, my objection is to the stating of the direction of flow. The uninformed reader will assume that he is being told this direction because it's a peculiarity of the LC circuit, unless he knows that this is simply conventional current flow direction. Why introduce something that complicates the explanation and gives the reader something else to think about? Sometimes, too much information is simply a confusion. Akld guy (talk) 20:27, 3 October 2019 (UTC)

I appreciate all the input. I still think the expanded wording could be helpful, but I understand your arguments and its not important enough to worry about. I accept the revert. Cheers --Chetvorno^TALK 00:46, 6 October 2019 (UTC)

I've copyedited the passage to something I think will have consensus. It begins with If an inductor is connected across a charged capacitor, the voltage across the capacitor will drive a current through the inductor,... SpinningSpark 16:32, 6 October 2019 (UTC)

Looks better --Chetvorno^TALK 19:45, 6 October 2019 (UTC)

Conflict between circuit diagram and equation: direction of inductor current flow vs. sign of V(t).

The circuit diagram shows current flowing out of the inductor's positive terminal. This is not the traditional representation, c.f. the Series LC Circuit below.

The issue causes confusion in the Solution section where V(t) is shown (as is traditional) as L * dV/dT and the negative sign in front of Omega0 after the cosine is differentiated.

You can easily see the diagram produces questionable results if you set L = 1 Henry, C = 1 Farad, V(0) = 0 Volts, and I(0) = 1 Amp. Referencing the diagram, it's clear that V(Δt) will be positive and the Solution will give V(Δt) as negative.

My suggestion would be to switch the inductor and capacitor in the diagram so that the orientation of voltage and current is tradition for the inductor.

Note it's true that this is arbitrary because with the change the capacitor's current flow is non-traditional. But one must be and the Solution's equation for V(t) makes it simpler to have the inductor's current direction traditional.

P.S. I found the issue by semi-blindly using the solution.

Michael Mulligan (talk) 05:00, 27 March 2020 (UTC)

Use of Both Upper- and Lower- case for Greek Phi is confusing.

In the middle of the "Solution" section, the text ("and the phase angle φ") uses the lower-case Greek phi (φ). The equations use upper-case Phi (Φ).

I would have made this relatively minor change but the equation and text fonts rendered the upper-case Phi different enough that I didn't think it was an improvement.

I'm too much of an amateur in Wikipedia editing to figure out how to get the fonts to match, but thought someone with more experience might make this fix trivially.

Michael Mulligan (talk) 05:10, 27 March 2020 (UTC)

Replace by: <math>\phi</math>. Result: $\phi$. --Ajv39 (talk) 12:49, 27 March 2020 (UTC)

Much better - thanks. Not sure why my attempt looked so bad. Michael Mulligan (talk) 17:07, 27 March 2020 (UTC)

Q discussions don't apply here

Since this article is strictly about the LC case, I don't think discussions of Q and bandwidth apply. -Roger (talk) 17:20, 27 February 2009 (UTC)

As above, real L and C always have some resistance, so Q is useful. Or, the other way around, an LC circuit has infinite Q. But real ones don't. Gah4 (talk) 01:29, 26 April 2021 (UTC)

order

I am wondering where in WP there is discussion about filter order. There is a little here, not much in RC or RL filters, and less in other filter related articles. Should there be a whole article discussing it? For one, I wanted a connection to db/octave in filter descriptions, which is commonly used instead of filter order, even though they are related. Gah4 (talk) 01:40, 26 April 2021 (UTC)

Merge with RLC article?

This and the RLC article are quite similar, and both seem somewhat incomplete. I suggest merging the two and treating the LC circuit as a special case. Thoughts? -Roger (talk) 17:18, 27 February 2009 (UTC)

I guess it could go either way. Of course, any LC circuit has resistance so the RLC analysis is the more complete one. However, the usage tuned circuit or tank circuit refers to an RLC circuit designed for the purpose of oscillating at a specific frequency, so the series resistance is made as low as possible to give it as high a Q as possible. So the LC circuit consists of an inductor and capacitor connected together, with no resistor. Maybe this should be explained in the article. --Chetvorno^TALK 20:11, 27 February 2009 (UTC)

Yes, the case of infinite resistance could be handled simply as a special case. -Roger (talk) 21:03, 27 February 2009 (UTC)

Superconductors

If an LC circuit were to be constructed entirely of superconducting materials, and all the necessary parameters (temperature of the material maintained at its superconducting temperature, and perhaps placing the apparatus in a vacuum to avoid loss of energy to the atmosphere) were used/applied, how close could such a circuit come to behaving as an "ideal" LC? Spiral5800 (talk) 15:35, 26 March 2011 (UTC)

Superconductors are actually being used for resonant circuits. They are not used for LC circuits AFAIK, but are used in the form of superconducting microwave cavity resonators. A microwave cavity is a hollow metal box with radio waves oscillating inside. It can be considered an LC circuit, the two walls of the cavity act like capacitor plates. As you suggested, by using superconductor the energy in the currents in the walls is not dissipated by resistance, so the oscillations last longer. Superconducting cavities are being used in scientific apparatus, particularly particle accelerators. How close a tuned circuit comes to "ideal" is measured by its Q factor, which is roughly how many cycles it takes for the oscillations to die out to 36% of their initial amplitude. A typical ordinary LC circuit has a Q of about 100; it takes 100 cycles for the oscillations to die out. Superconductive cavities can have Qs of 400,000. (Lancaster, p. 83) --Chetvorno^TALK 18:50, 26 March 2011 (UTC)

Thank you greatly for this thorough and informed response! Spiral5800 (talk) 20:07, 2 April 2011 (UTC)

If you made a superconducting solenoid and parallel-plate capacitor, there could still be losses due to the circuit acting as an antenna and radiating energy as electromagnetic waves. There are ways to deal with that too, but it's just worth noting that resistive losses aren't the only reason the circuit might not behave as an ideal LC.--JB Gnome (talk) 23:45, 15 July 2012 (UTC)

Proposed addition to article

I'd like to add this material but it may be too technical for the article.

A capacitor stores energy in an electric field (depending on the voltage across it), an inductor stores energy in a magnetic field (depending on the current through it). If we start with a charged capacitor and connect an inductor across it, current will start to flow out of the capacitor (reducing the voltage across it) through the inductor, building up an magnetic field around the inductor. Eventually the capacitor will have no energy in it, but the inductor will be storing energy in its magnetic field. With no voltage across it the current will slow, and energy will be extracted from the magnetic field to keep the current flowing. Energy will therefore be extracted from the magnetic field, producing a current which will charge the capacitor with a voltage of opposite polarity to what it possessed originally. When the magnetic field is completely dissipated all the energy will again be stored in the capacitor (with the opposite polarity) and the process will repeat in reverse.

I wanted to avoid that E=.5*C*V^2 and E=.5*L*I^2 so said 'depending on' but that might be sacrificing accuracy for simplicty, and not that simple. other problems. Can anyone clean it up to usable form? RJFJR 07:10, Mar 26, 2005 (UTC)

Looks fine to me. Just put it in and it will be tweaked as part of the article. — Omegatron 14:58, August 22, 2005 (UTC)

I'd say that information is the opposite of technical, compared to the information that is already there. I can understand it, though I'd quibble with "all the energy". It needs some phrasing tweaks in the bit "and energy will be extracted from the magnetic field to keep the current flowing. Energy will therefore be extracted from the magnetic field, producing a current". I notice the information is not now present (1 year 1 month later). Too bad, this is the sort of description Wikipedia needs.

I added it.--Chetvorno^TALK 21:48, 22 May 2008 (UTC)

I just wanted to say that the paragraph you quote above is the clearest and most-easily understood discussion of the LC relationship I've ever seen. I now understand the concepts, and I think the comparisons with a pendulum and sloshing water were brilliant. If this is a community effort, bravo to all! Prof. Todd Carney / Southern Oregon University 05:09, 12 August 2011 (UTC) — Preceding unsigned comment added by Tcarney57 (talk • contribs)

Unfortunately it is not correct - the absence of a voltage between the terminals of an inductor will not cause the current to diminish - it is the rising voltage of the capacitor in opposition to the current which causes that. The text as it now stands in the article is better. However, I query this: "However, the current will continue, because inductors resist changes in current." I am not sure that this actually means anything. It is like the Platonic theory of gravity - stones fall because they have a tendency to do so. Why do inductors resist changes in current ? Answering this question is crucial to giving an explanation that actually !explains!. It might be difficult or impossible to do so (why do masses obey Newton's first law ?) but if this is the case the 'because' and what comes after it should be deleted. Likewise this: "The energy to keep it flowing is extracted from the magnetic field ..." The use of the passive "is extracted" fogs the issue and makes it look as though this is an act of god, or some such. Who or what does the extracting ? Again a REAL explanation would be much better than this pretence. G4oep (talk) 15:40, 11 January 2015 (UTC)

This is just an explanation in simple terms, avoiding technical jargon, for general readers. There is a circuit analysis below for those who want more information. I think the phrase "The energy to keep it flowing is extracted from the magnetic field..." is clear, explained by the 3rd sentence in the section "An inductor stores energy in its magnetic field..." It takes energy to charge the capacitor back up. Where does it come from? The inductor's magnetic field. The phrase "...inductors resist changes in current." is simply a statement of Faraday's law of induction. The current through an inductor cannot change discontinuously because it would require an infinite induced EMF. There is no point in complicating the explanation until it confuses nontechnical readers. WP is a general-interest encyclopedia. Nontechnical readers, who will probably be the majority of readers coming to the article, deserve an explanation that they can understand. This is a huge, major shortcoming in many WP technical articles. The existing content is superlatively praised above by a university professor, a professional whose job it is to teach this stuff. My feeling is that's a strong argument for keeping it as it is. --Chetvorno^TALK 20:34, 11 January 2015 (UTC)

Sorry - I don't like to seem argumentative, and I respect your opinion, but I really feel that the "because" I refer to is nonsense. Even (particularly) beginners deserve a clear and accurate explanation, or admission of defeat if no-one is able to provide one. Yes - Faraday's Law is what it's about, like Newton's Law in the case of mass. But these are (as far as I am aware), purely empirical laws, and do not provide explanations; it is this that makes "because" inappropriate. Newton had the good sense to say "Hypotheses non fingo" - I frame no hypotheses, and I am not aware that Faraday included any "because" when putting forward his law. "The energy to keep it flowing is extracted from the magnetic field..." is certainly clear, but it might convey the idea that in order for the current to continue, energy (or power) is required, which is incorrect in general; it is only true in that the current which continues to flow charges a capacitor in this case. How about this as an alternative: "However, the current could continue unchanged in accordance with Faraday's law of induction, which requires that for the current to change in an inductor, a voltage must be applied (which is analogous to Newton's First Law for velocity, mass and force). No energy is required for this provided the current remains constant. However, as the current continues to flow, the capacitor will acquire charge, and its terminal voltage will rise. This applies a voltage to the inductor which is in opposition to its current, which now falls; again this in accordance with Faraday's Law. The falling inductor current and rising capacitor voltage indicate a transfer of energy from the inductor to the capacitor. This is analogous to a moving mass colliding with a spring, and compressing it." G4oep (talk) 10:29, 12 January 2015 (UTC)

G4oep's edits to the description contain some good additions, such as Faraday's law, but just as many bad ones. The added sentence "No energy is required for this provided the current remains constant" is misleading on two levels. No energy is required for a constant current through the inductor, but the inductor is attached to the capacitor; a constant current in the circuit would require energy to charge it. And of course the current through the inductor in a tuned circuit is never constant. Several sentences later the description says energy is transferred, this will be confusing. In addition, a second unnecessary harmonic oscillator analogy has been added to the description: "This is analogous to a moving mass colliding with a spring, and compressing it." The circuit is already compared to a pendulum harmonic oscillator, which is likely to be more familiar to readers; why can't we stick to one analogy? Also the circuit is not analogous to a mass "colliding" with a spring, but to a mass attached to a spring. I don't see that the additional complication and confusion for nontechnical readers, as well as the addition of the pedantic, jargon-ridden language, is worth it. --Chetvorno^TALK 21:24, 15 January 2015 (UTC)

Make your own LC circuit with LED

Can some one teach me how. I want to put my knowledge to use 136.158.11.140 (talk) 05:40, 9 January 2022 (UTC)

As someone else noted, this is for discussing improvements to the article. LC circuits are commonly used for filters and oscillators, and don't normally work (directly) with LEDs. An LC based oscillator could be connected to an LED, but that isn't enough of a connection to apply to this article, or the LED article. You need to separately learn how to design LC oscillators and how to power LEDs. Because of WP:NOTHOWTO it wouldn't go here, even if it was otherwise applicable. Gah4 (talk) 03:36, 10 January 2022 (UTC)

Resonant Frequency - Algorithm Correction

The Algorithm presented for finding the Resonant Frequency declares that ƒ is equal to an irrational expression: $f={1 \over {2\pi {\sqrt {LC}}}}$.

Using the method of Rationalizing the Denominator, the Algorithm should be rewritten as: $f={{\sqrt {LC}} \over {2\pi LC}}$

This is not a serious issue; however, to some it appears very improper. —Preceding unsigned comment added by 75.89.6.226 (talk) 01:29, 14 April 2008 (UTC)

Complete rot, expressions are best given in their minimised form. Rationalising roots is an exercise in arithmetic given to schoolchildren to fill up their otherwise empty day. SpinningSpark 18:38, 26 July 2008 (UTC)

Even more, rationalizing roots only makes sense when the root is of a rational number. As written, we don't know that L and C are rational. (Though they are commonly rounded to nearby rational values.). Gah4 (talk) 01:27, 26 April 2021 (UTC)

Time domain solution

I was looking at the "time domain solution" section to practice differential equations for math course at the university, but I was not able to understand the "After rearranging and substituting, we obtain the second order differential equation" step, as there was no way for me, with my basic math knowledge and no knowledge at all about circuits, voltage and current, to understand how you can obtain the ::${\frac {d^{2}i(t)}{dt^{2}}}+{\frac {1}{LC}}i(t)=0.\,$ from the previous equations. I found a (aparently) good explanation here, [1], I was thinking of including some of these formulas to fill in the missing steps, do you think it would be useful, or it will just make the "time domain solution" too long?

--Marco4math (talk) 20:34, 15 October 2009 (UTC)

I don't think there are more steps in the source you link (fewer if anything), but it is a slightly different presentation to Wikipedia and also involves an uneccessary additional variable (q). The thing that is not clear in our article is that "substituting" means substitute the element equations into the circuit voltage equation and "rearranging" involves differentiating the expression. I have removed your addition of that as an external link, there is no real need for it, the presentation in the article can be improved if necessary. SpinningSpark 01:05, 16 October 2009 (UTC)

I actually found the link very very useful to understand as sin and cosine are more natural to understand for me than exponentials. — Preceding unsigned comment added by 188.86.95.235 (talk) 18:22, 13 May 2012 (UTC)

Wrong conclusion

The LC_circuit#Applications_of_resonance_effect section say "A series resonant circuit provides voltage magnification." and "A parallel resonant circuit provides current magnification.", but these conclusions do not realy match the equation $\lim _{\omega ^{2}LC\to 1}Z=\infty$. Since $U=Z\cdot I$ still applies, this results in $U=Z\cdot I=\infty \cdot I=\infty$ for a parallel LC circuit. So a parallel resonant circuit provides voltage magnification and a series resonant circuit provides current magnification.

--145.116.41.255 (talk) 14:00, 21 September 2012 (UTC)

Yes, but for instance in the series resonant circuit, the input current is always exactly the same as the output current. It may be large at resonance if the source is a voltage source, limited only by R, or it may be limited by the source also - in the case of an ideal current source it will not change at all with frequency. On the other hand, the voltage across the inductor (or capacitor) is enormously greater than the input voltage in all cases. Similarly the current through L or C in the parallel circuit is enormously greater than the input current. SpinningSpark 16:43, 21 September 2012 (UTC)

New section "Series configuration"

I think the recently added section "Series configuration" gives an erroneous view of the LC circuit and should be removed. The section it was added to originally described natural (undriven) oscillations of the LC circuit. There is no difference between a series and parallel LC circuit for undriven oscillations but the addition seems to say there is. All the new section describes is a different initial condition of the circuit (magnetic flux instead of charged capacitor). It's unnecessary. The change is a degradation of what was originally the best part of the article. --Chetvorno^TALK 17:50, 8 October 2012 (UTC)

It's not there any more, right? SpinningSpark 00:25, 9 October 2012 (UTC)

He re-added it as a single section, but I reverted it. First Harmonic, I feel the article was better in its original form. Your addition describes the resonance oscillation process a second time as if it is a different process, but you are actually describing the same oscillation, just started at a different point in the cycle by a different initial condition. --Chetvorno^TALK 03:45, 9 October 2012 (UTC)

When you refer to "your addition" I am assuming you are talking to First Harmonic; I haven't added anything, at least not recently. I agree we don't want to describe the whole oscillation as a new process, but still, it is a worthwile addition and clarification that oscillation can be initiated by a charge of magnetic energy as well as from an electrostatic charge. SpinningSpark 12:51, 9 October 2012 (UTC)

Yes, I was addressing First Harmonic. My feeling is that his addition isn't useful. This is just a qualitative description of how oscillation works in an LC circuit, for nontechnical readers. It doesn't cover, and doesn't have to cover, every situation. His version is repetitive, and is giving nontechnical readers an erroneous impression about the process. This used to be the best part of the article, praised on the talk page. Why mess it up? --Chetvorno^TALK 16:07, 9 October 2012 (UTC)