Talk:Faraday's law of induction/Archive 3

Archive 1

Archive 2

Archive 3

Archive 4

Relation btwn "classical faraday's law" and maxwell-faraday equation

Hi Michael Lenz, I have various questions about your recent edits :-)

• Are we sure that Faraday's law (or "classical faraday's law" or "flux rule" or whatever you want to call it) is only approximate at relativistic velocities? When you change reference frames, three things happen: (1) The forces on the electrons are transformed, (2) the geometry of the circuit is transformed, and (3) the electric and magnetic fields are transformed. Yes, I understand, if you ignore the first two effects and take a linear approximation of the third effect, you get Faraday's law. [That's the approach in your edit, and in Jackson's textbook chapter 5 which I guess you read!] But I also believe that if you treat all three effects exactly, you still get precisely Faraday's law--the higher order corrections to (1),(2),(3) may cancel each other out. Do we have any references on this? I don't recall seeing anyone claim that Faraday's law is not exact for relativistically-moving wire loops.
• If I understand it correctly, the text argues that Faraday's law in general can be derived from the Maxwell-Faraday equation and the relativistic transformation of fields. I disagree...Faraday's law covers the case of wire loops that are deforming, not just linearly translating. A deforming loop cannot be Lorentz-transformed into a stationary loop on which Maxwell-Faraday can directly apply. To cover the general case you need to use the more complicated derivation where Maxwell-Faraday and the Lorentz force are both used explicitly and different parts of the loop can have different velocities.
• Readers may be misled by the claim "Maxwell-Faraday law applies to circuits in motion." They are apt to just simply apply the law as stated to a moving circuit, replacing the partial time derivative by a total time derivative, and they'll get the wrong answer. What is intended is "Maxwell-Faraday only applies to circuits at rest, but luckily circuits in linearly-translating motion can be Lorentz-boosted to circuits at rest, and then you can use Maxwell-Faraday law there, and then boost back". This is a somewhat more subtle statement. I wonder why it's so important to emphasize. Isn't it usually easier to just use the Lorentz force equation and not change frame at all?

Thanks in advance!! :-) --Steve (talk) 23:09, 11 August 2011 (UTC)

Hi Steve, good to get such a quick response to my edits. I expected some kind of "protest", so I am quite well prepared :-)

• Are we sure that Faraday's law (or "classical faraday's law" or "flux rule" or whatever you want to call it) is only approximate at relativistic velocities?

Well, I will leave the question about the right name ("classical Faraday's law", "flux rule" etc.) up to you native speakers and concentrate on the correct physical interpretation :-)

First of all, let me say that we are sure that the Maxwell-Faraday equation is correct even at relativistic velocities. A proof for that is given in "Károly Simonyi, Theoretische Elektrotechnik, VEB Deutscher Verlag der Wissenschaften, Berlin, 1973". I followed all calculations by myself and found no mistakes. (Another proof -- the original one, so to say -- is given by Einstein in his famous work "Zur Elektrodynamik bewegter Körper" written in 1905. I only read this work partly, however.)

The point is, if we take a correct equation (the Maxwell-Faraday equation) and insert an approximation (${\vec {E}}\approx {\vec {E}}'-{\vec {v}}\times {\vec {B}}$), then the result (the classical formulation of Faraday's law) must inevitably be called an approximation.

• But I also believe that if you treat all three effects exactly, you still get precisely Faraday's law--the higher order corrections to (1),(2),(3) may cancel each other out. [...] I don't recall seeing anyone claim that Faraday's law is not exact for relativistically-moving wire loops.

I got your point. If you agree that

$\oint _{C}{({\vec {E}}'-{\vec {v}}\times {\vec {B}})}\;{\text{d}}{\vec {s}}\approx -\int _{A}{\frac {\partial {\vec {B}}}{\partial t}}\;{\text{d}}{\vec {A}}$

is a correct representation of the classical version of faraday's law, then the problem should be solved with my above argumentation.

If you, however, think that I did not write down the classical Faraday's law correctly, let me know and write down what you think is the correct representation.

We can then check whether "your" representation is compatible with the special relativity theory. All we have to do is to insert the (exact!) Lorentz transformations of x,y,z,t,B and E into it and see whether its mathematical structure remains the same after the transformation. (Because of the numerous residual terms of the exact transformation, this is tiresome, but we should do that nevertheless.)

• Do we have any references on this?

You can find a reference for that here. I refer to page 47/48 and start translating after equation (3.82):

"Although the values of the electromagnetic field quantities depend on the frame of reference, the shape of Maxwell's equations are the same in all inertial systems (Principle of relativity, Invariance of Maxwell's equations). So, the second of Maxwell's equations can be written in the frame at rest and in the moving frame as follows:

$\oint \limits _{C}{\mathbf {E} }\ {\text{d}}\mathbf {s} =-\int \limits _{A}{\frac {\partial \mathbf {B} }{\partial t}}\ {\text{d}}\mathbf {A}$

$\oint \limits _{C'}{\mathbf {E'} }\ {\text{d}}\mathbf {s'} =-\int \limits _{A'}{\frac {\partial \mathbf {B'} }{\partial t'}}\ {\text{d}}\mathbf {A'}$

(eq. 3.83)

For small relative velocities, while considering ${\vec {E}}={\vec {E}}'-{\vec {v}}\times {\vec {B}}$, the "mixed" representation

$\oint _{C}{({\vec {E}}'-{\vec {v}}\times {\vec {B}})}\;{\text{d}}{\vec {s}}=-\int _{A}{\frac {\partial {\vec {B}}}{\partial t}}\;{\text{d}}{\vec {A}}$

is sometimes used, which can be separated into a time-dependent and a motion-dependent term [Kli03]:

$\oint _{C}{{\vec {E}}'}\;{\text{d}}{\vec {s}}=-\int _{A}{\frac {\partial {\vec {B}}}{\partial t}}\;{\text{d}}{\vec {A}}+\oint _{C}{({\vec {v}}\times {\vec {B}})}\;{\text{d}}{\vec {s}}$

(3.85)

This is the "Law of Induction for moving bodies" going back to Maxwell and Hertz, which applies for small velocities with $\beta =v/c_{0}\ll 1$ by approximation. Usually, the right side of (3.85) is written as a total differential:

$\oint _{C}{{\vec {E}}';{\text{d}}{\vec {s}}}=-{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{A}{\vec {B}}\;{\text{d}}{\vec {A}}=-{\frac {{\text{d}}\Phi }{{\text{d}}t}}$

(3.86)[...].

${\vec {E}}'$ is measured in the moving frame of reference, while the path integration is carried out in the frame at rest. The path integral on the left sidde of (3.86) is therefore neither the induction voltage u' in the moving frame nor u in the frame at rest. [...]" (end of translation, equations have been slightly changed in notation).

• Faraday's law covers the case of wire loops that are deforming, not just linearly translating. A deforming loop cannot be Lorentz-transformed into a stationary loop on which Maxwell-Faraday can directly apply.

I agree that a deforming loop cannot be Lorentz-transformed as a whole. However, the Maxwell-Faraday law does not require any Lorentz transformation at all.

To be convinced, have a look at the equation:

$\oint \limits _{C}{\mathbf {E} }\ {\text{d}}\mathbf {s} =-\int \limits _{A}{\frac {\partial \mathbf {B} }{\partial t}}\ {\text{d}}\mathbf {A}$

Do you see any inverted comma (') indicating that a Lorentz boost is needed, here? I am sure, you don't!

The truth is that it's the classical Faraday's law that requires the Lorentz boosts:

$\oint _{C}{({\vec {E}}'-{\vec {v}}\times {\vec {B}})}\;{\text{d}}{\vec {s}}\approx -\int _{A}{\frac {\partial {\vec {B}}}{\partial t}}\;{\text{d}}{\vec {A}}$

$E'$ is the electric field at the path increment ${\text{d}}{\vec {s}}$ measured from the moving frame of reference. Since $v$ can be different for the different path increments, the classical version of Faraday's law requires not only one single, but up to an infinite number of Lorentz boosts; one boost for each path increment.

Here you see that -- although it is not possible to Lorentz-transform the loop as a whole -- it is still possible to transform it piece by piece.

• Readers may be misled by the claim "Maxwell-Faraday law applies to circuits in motion."
• What is intended is "Maxwell-Faraday only applies to circuits at rest, but luckily circuits in linearly-translating motion can be Lorentz-boosted to circuits at rest, and then you can use Maxwell-Faraday law there, and then boost back"

No, you are definitely on the wrong track. The readers are not misled. They are led to the truth!

Things really appear different than they are, here.

As I already mentioned before, it's the classical Faraday's law that comes along with the Lorentz boost, and it's the Maxwell-Faraday law that is formulated for a situation without Lorentz-boost.

Moving conductor in a magnetic field.

To make the arguments clear, let's discuss a concrete example and have a look at the moving metal bar in a magnetic field (constant in time and space) depicted on the right side.

The wires and the electrical terminal are at rest, while the (ideally conducting) metal bar moves to the right with velocity $v$. The observer is situated at the frame at rest. You certainly agree that he sees a voltage $U\neq 0$ at the terminal, and an electric field $E=0$ within the wires on the left, on top and at the bottom. But what electric field does the observer at rest see inside the moving metal bar?

Despite general belief to the contrary, the answer $E=0$ is wrong, although the metal might be ideally conducting! The correct answer is that he sees

${\vec {E}}=\gamma \left({\vec {E}}'-{\vec {v}}\times {\vec {B}}'\right)+(1-\gamma ){\frac {{\vec {E}}'\cdot (-{\vec {v}})}{{v}^{2}}}(-{\vec {v}})=-\gamma \left({\vec {v}}\times {\vec {B}}'\right)\approx -{\vec {v}}\times {\vec {B}}$. (The complicated term comes from the exact inverse Lorentz transformation. You need to use the inverse transformation which is not explained in the article. To get it, swap the primed with the unprimed variables, and replace $v$ by $-v$. Then enter $E'=0$, the electric field in the metal bar observed in the frame at motion.

A theoretical approach of understanding is considering that ${\text{curl}}{\vec {E}}=-{\dot {\vec {B}}}=0$. This means that the E-field is a conservative vector field without any closed field line. In other words: This example shows no induction at all!

An easier approach is by considering the forces that are applied to an electron with charge $q$ being located inside the metal bar.

Looking at the electron from the perspective of an observer "riding" on the electron, we see no force at all. There is no electric force, because $E'=0$ as a result of the high conductivity of the metal, and there is no magnetic force either, because we sit on the electron, and thus, there is no relativ velocity. This is quite easy to understand. However, our frame of reference is that of an observer at rest and thus different from the one discussed here.

Looking at the electron from the frame at rest, we see a Lorentz force ${\vec {F}}_{L}=q{\vec {v}}\times {\vec {B}}$. Because we see that the electron is not accelerated, we can conclude that the overall force on the electron is ${\vec {F}}=0$. But what compensates the Lorentz force? Oviously, there must be an electric force ${\vec {F}}_{C}=q{\vec {E}}$ with the electric field strength ${\vec {E}}\approx {\vec {E}}'-{\vec {v}}\times {\vec {B}}=0-{\vec {v}}\times {\vec {B}}=-{\vec {v}}\times {\vec {B}}$. This is the field that we already know from the Lorentz transformation. So ${\vec {F}}={\vec {F}}_{C}+{\vec {F}}_{L}=0$.,

Please note that -- when we talk about classical forces with three components for the x-, y-, and z-directions in general, and the Lorentz force in particular -- we implicitely do a non-relativistic approximation. On the contrary, relativistic forces are always given as a Four-vector. So don't be misguided by the fact that we got an exact cancellation of forces while using the approximated Lorentz transformation, whereas we would have gotten only an approximated cancellation of forces, if we had used the exact Lorentz transformation. Both is alright, because 3-element-forces are not compatible to the special relativity theory.

Best regards, Michael Lenz (talk) 22:14, 12 August 2011 (UTC)

I agree that the Maxwell-Faraday equation is correct always.

This unpublished paper argues in detail that classical Faraday's law is exactly true for relativistically-moving loops. It also argues in detail that classical Faraday's law cannot be derived from the Maxwell-Faraday equation alone: It requires all of Maxwell's equations plus the Lorentz force.

I do not agree that

$\oint _{C}{({\vec {E}}'-{\vec {v}}\times {\vec {B}})}\;{\text{d}}{\vec {s}}\approx -\int _{A}{\frac {\partial {\vec {B}}}{\partial t}}\;{\text{d}}{\vec {A}}$

is a correct representation of classical Faraday's law. The correct representation, as stated in the article and in textbooks, is:

EMF = -d(flux)/dt.

Everything else must come directly from this equation. For a loop moving at constant velocity v (in the "lab frame"), the exact formula for EMF is:

EMF = $\oint _{C}{\vec {E}}+{\vec {v}}\times {\vec {B}}$

by the Lorentz force law. E and B are the electric and magnetic field in the lab frame, and C is the contour in the lab frame (not the rest frame of the circuit).

Eq. (3.85) is an integral of the electric field in the moving frame, integrated over the contour in the frame at rest. This is a nonsense quantity: You cannot mix together frames like that. It is only an approximation to EMF. Likewise, the quantity $E'-v\times B$ does not represent anything meaningful, it is a nonsense mixture of the electric field in the one frame with the magnetic field in a different frame.

I agree that the Maxwell-Faraday equation does not require Lorentz boosts. But neither does the classical Faraday law:

EMF = -d(flux)/dt.

Do you see any inverted commas ("primed quantities") (')? :-)

I agree with everything in your example (except for the pessimistic statement that there is "general belief to the contrary"!). I hope you also agree that if the terminals were connected (i.e., if the place where you wrote "U" was a continuous wire instead of a broken wire), and the sliding metal bar was replaced by a sliding resistor, then the situation would be opposite: E=0 and E'≠0. --Steve (talk) 14:34, 14 August 2011 (UTC)

Hello Steve,

• (except for the pessimistic statement that there is "general belief to the contrary"!)

I hope you didn't understand that as a personal offence, because it wasn't meant one.

The pessimistic statement about the general belief to the contrary is my impression about what I read in introductory textbooks about physics and engineering (mostly in German) and a point that I often noticed in previous discussions at the university. I wanted to emphasize this point to avoid potential misunderstandings.

Let me sum up where we agree and what questions remain. We agree that

• Maxwell-Faraday is relativistically correct
• that the equation $\oint _{C}{({\vec {E}}'-{\vec {v}}\times {\vec {B}})}\;{\text{d}}{\vec {s}}\approx -\int _{A}{\frac {\partial {\vec {B}}}{\partial t}}\;{\text{d}}{\vec {A}}$ is not 100% sound (You say, it's nonsense. I wouldn't go that far, however.)
• if the terminals were connected (i.e., if the place where you wrote "U" was a continuous wire instead of a broken wire), and the sliding metal bar was replaced by a sliding resistor, then the situation would be opposite: E=0 and E'≠0.

The following questions are not yet cleared

• the (nonsense or not) mixture of the electric field in the one frame with the magnetic field in a different frame
• the correct representation of the (classical) Faraday's law.

The first point was discussed in the book that I quoted. Unfortunately, I omitted translating the part we're discussing right now (see my [...] in the former text). I'll begin the translation right after eq. 3.87:

The voltage induced in the loop C is thus approximately equal to the temporal change of the magnetic flux in the area that is bounded by contour C. ${\vec {E}}'$ is measured in the moving frame of reference, whereas the path integration is carried out in the frame at rest. The path integral on the left side of (3.86) is therefore neither the induction voltage u' in the moving frame nor u in the frame at rest. Because it is possible for small velocities $\beta =v/c_{0}\ll 1$ to approximate $d{\vec {s}}\approx d{\vec {s}}'$ and $C\approx C'$, the induced voltage in the loop C can be determined with the above equation by approximation. [...]

I think, the author just forgot to mention that for small velocities the following approximations apply ${\text{d}}t\approx {\text{d}}t'$, ~~ ${\text{d}}A\approx {\text{d}}A'$ and ${\text{d}}B\approx {\text{d}}B'$.

Considering these approximations, we can conclude, that eq. (3.86) is meaningful for small velocities, but not for fast ones.

I think, you understand now, why I think that the classical Faraday's law (which is consider to be equal to eq. 86) is an approximation.

Now, as far as I understand you, you consider the following equation to be the correct representation of the classical Faraday's law

$\oint _{\partial \Sigma (t)}\left(\mathbf {E} (\mathbf {r} ,\ t)+\mathbf {v\times B} (\mathbf {r} ,\ t)\right)\cdot d{\boldsymbol {\ell }}\ \ =-{\frac {d}{dt}}\iint _{\Sigma (t)}d{\boldsymbol {A}}\cdot \mathbf {B} (\mathbf {r} ,\ t)\ ,$

I will write the equation in another notation:

$\oint _{C}\left({\vec {E}}+{\vec {v}}\times {\vec {B}}\right){\text{d}}{\vec {s}}=-{\frac {\text{d}}{{\text{d}}t}}\int _{A}{\vec {B}}\cdot d{\vec {A}}$

To resolve the integral, we can use the following equation. I remember reading the proof for this equation. It includes some differential geometry and the equation divB=0, which should be non-controversial:

${\frac {\text{d}}{{\text{d}}t}}\int {\vec {B}}\;{\text{d}}{\vec {A}}=\;\int {\frac {\partial {\vec {B}}}{\partial t}}{\text{d}}{\vec {A}}-\oint _{\partial A}{({\vec {v}}\times {\vec {B}})}{\text{d}}{\vec {s}}$

Combining the last two equations leads to:

$\oint _{C}\left({\vec {E}}+{\vec {v}}\times {\vec {B}}\right){\text{d}}{\vec {s}}=-\;\int {\frac {\partial {\vec {B}}}{\partial t}}{\text{d}}{\vec {A}}+\oint _{C}{({\vec {v}}\times {\vec {B}})}{\text{d}}{\vec {s}}$

This, however, is equivalent to the Maxwell-Faraday equation (without any approximation)

$\oint _{C}vec{E}{\text{d}}{\vec {s}}=-\;\int {\frac {\partial {\vec {B}}}{\partial t}}{\text{d}}{\vec {A}}$

So "your" classical Faraday's law is completely equivalent to $curlE=-{\dot {\vec {B}}}$, as long as divB=0 (which is supposed to be always true).

So we are now sure that the physics is represented correctly in the article. Interestingly, the proof did not need the Lorentz force anywhere, but just divB=0 and some differential geometry. You cited an article which (you said) needed the Lorentz force.

Some part of our misunderstanding was due to the fact that my understanding of what is the classical Faraday's law is different from yours. For name-giving in the English wikipedia, however, only the English-speaking literature is relevant. My personal opinion and German literature is not relevant to that.

However, there is another problem that we should address in the article. The definition of the EMF that the wikipedia article gives, is different from the one I know and from the on that, for example, Raymond A. Serway and John W. Jewett (Jr) give:

Wikipedia: $EMF=\oint _{C}\left({\vec {E}}+{\vec {v}}\times {\vec {B}}\right){\text{d}}{\vec {s}}$

Serway/Jewett: $EMF=\oint _{C}{\vec {E}}{\text{d}}{\vec {s}}$ (look between equation 31.8 and 31.9). (Serway and Jewett also give a wrong representation of Faraday's law.)

There seems to be some confusion in other books, too:

This book gives the wikipedia-definition of the EMF.

This book gives a wrong Faraday's law and defines the EMF using the magnetic flux.

This book knows "my" approximated approach, but doesn't say that it is an approximation (it rather says: "rigorous"). It defines the EMF in the same way as you do.

This book, begins with the correct Faraday's law and erroneously draws the d/dt from inside the integral to the outside, which is correct for $v=0$ only.

Here, you find "my" definition of the EMF and a wrong representation of Faraday's law.

Here again you find "my" definition of the EMF.

Again "my" definition of the EMF, now called "induced" EMF (perhaps that again is something different).

This book is contradictive (your definition and mine on the same page).

And again.

And again.

So as a first thing, I'll comment out my changes to the article. We should then discuss how to improve the article to make the topic clear to the reader and help him to understand the (numerous) mistakes in the literature.

Best regards, Michael Lenz (talk) 19:07, 14 August 2011 (UTC)

For definitions of EMF, you left out what I always thought was the primary definition:

EMF is the work done per unit charge traversing the circuit

Maybe I'm partial because that's the definition I was taught (from Intro to Electrodynamics by Griffiths). But it's also the primary definition in the wikipedia article Electromotive force. It's also the only definition that works for batteries, where some of the work is due to chemical reactions instead of electromagnetic forces. I looked on google books myself and found this definition in lots of places when you search for "electromotive force" in general instead of searching specifically for Faraday's law. For example...

• Tipler and Mosca introductory textbook, "The work per unit charge is called the EMF"
• Physics Insights O-level textbook, "The emf of any electrical source is the work done by the source in driving a unit charge around a complete circuit"
• Lerner textbook, "The external work per unit charge..."
• Griffiths' electromagnetism textbook (as I mentioned)
• Feynman Lectures on Physics: "The emf is defined as the tangential force per unit charge in the wire integrated over length once around the complete circuit".
• Look through the sources for the article electromotive force, they almost all use this definition.

I'm not cherry-picking, take a look...

According to the work-per-charge definition of EMF, the statement "EMF of a wire loop is the integral of (E + v x B)" is not a definition it is a theorem, more specifically a consequence of the Lorentz force law. That's why I said that the Lorentz force law is involved in deriving classical Faraday's law from Maxwell-Faraday equation or vice-versa.

I admit it's hard to prove this, but I would say that work-per-charge is not only the primary definition of EMF, it is the universal definition of EMF. When textbook authors give different definitions, that's because they are discussing special cases and want to simplify and approximate things. :-) --Steve (talk) 15:36, 27 August 2011 (UTC)

I left out this "definition", because it is not precise. For example, it does not tell us how fast to move the unit charge around the loop, and it does not tell us whether the charge is located at all places around the loop at the same time or not. The integral does tell us: If you look at the definition $EMF=\oint \limits _{\partial A}({\vec {E}}+{\vec {v}}\times {\vec {B}}){\text{d}}{\vec {s}}$, you will find that the summation takes place at all places around the loop at the same time and that there is no movement of any charge at all. Here, the linguistic expression is the approximation (a close one, admittedly), whereas the mathematical term is the "true" definition. By the way: You do not need to have any idea about the Lorentz force to show the equivalence of "curl E = -dot B" and Faraday's law. All you need is mathematics, here. Michael Lenz (talk) 23:24, 26 September 2011 (UTC)

Now, we have another problem

Steve, if Faraday's law is equivalent to $curl{\vec {E}}=-{\dot {\vec {B}}}$, then it does not include two phenomena: It is just the Maxwell-Faraday equation with the term $\oint {\vec {v}}\times {\vec {B}}{\text{d}}{\vec {s}}$ added to both sides of the equation. You could as well add anything else. So the second paragraph saying that it includes two phenomena is not yet satisfactory. Michael Lenz (talk) 19:36, 14 August 2011 (UTC)

I've understood now what annoyed me. When the authors write that two phenomena are included in Faraday's law, they mean that the two phenomena are included in the EMF. In my opinion, we should add an explanation about why we define the EMF in the way we do (and keep the current definition, because it is excellent). Taking into account ${\vec {E}}'\approx {\vec {E}}+{\vec {v}}\times {\vec {B}}$, we find that

$EMF=\oint ({\vec {E}}+{\vec {v}}\times {\vec {B}}){\text{d}}{\vec {s}}\approx \oint {\vec {E'}}{\text{d}}{\vec {s}}$

Considering that ${\vec {E}}'=0$ in the metal wire, the EMF is thus equal to the terminal voltage for $v\ll c$, no matter if the wire is moving or not. So with the EMF, we have a direct linkt to what we can measure with an oscilloscope. (I think this was the aim of the book that I had cited.)

I'll do some changes on that and also correct the following equation

$\oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\ \iint _{\Sigma }{\partial \over {\partial t}}\mathbf {B} \cdot d\mathbf {A} =-\ {\partial \over {\partial t}}\iint _{\Sigma }\mathbf {B} \cdot d\mathbf {A}$

which I found in "The Maxwell-Faraday equation". (d/dt cannot be drawn out of the integral in general. I know that "The Maxwell-Faraday equation" was intended for v=0, but we have seen that this restriction is not necessary.) Feel free to add things or rechange (and correct the article if my English sounds odd). Best regards, Michael Lenz (talk) 21:12, 14 August 2011 (UTC)

If EMF is defined as "work per unit charge traversing the circuit", then the two phenomena are "EMF is generated when a changing magnetic field induces an electric field that does work on the electrons" and "EMF is generated when a magnetic field redirects the motion of a wire into doing work on the electrons in the wire". I would say these are "two phenomena" that are "included in Faraday's law", wouldn't you? :-) (Of course, the former is because of the Maxwell-Faraday equation, the latter is because of the Lorentz force law.)

The definition "EMF is what is measured if you put an ideal voltmeter in the loop somewhere" is fine, and is exactly equivalent to "EMF is the work required to send a unit charge around the loop once". Incidentally, in neither case do you need to assume the conductivity of the loop is infinite, as you've been doing. With the voltmeter definition, the current is zero because the voltmeter is ideal, so the wire has no voltage drop anywhere except the voltmeter. With the work-per-charge definition, you actually need finite conductivity, then the work of moving the charge around the loop ends up as heat. :-) --Steve (talk) 19:58, 27 August 2011 (UTC)

There are no "counterexamples" to Faraday's law

Counterexamples

• 
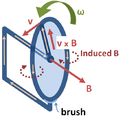
  Faraday's disc electric generator.

The text says: Although Faraday's law is always true for loops of thin wire, it can give the wrong result if naively extrapolated to other contexts. One example is the homopolar generator (above left): A spinning circular metal disc in a homogeneous magnetic field generates a DC (constant in time) EMF. In Faraday's law, EMF is the time-derivative of flux, so a DC EMF is only possible if the magnetic flux is getting uniformly larger and larger perpetually. But in the generator, the magnetic field is constant and the disc stays in the same position, so no magnetic fluxes are growing larger and larger. So this example cannot be analyzed directly with Faraday's law.

The text about Faraday's disc is misleading and requires complete revision.

1. The first misconception comprised in the text is that Faraday's law requires some loop of thin wire. Colleagues, please understand that there is no need for any wire at all. The integral requires a (mathematical) path, nothing more!

2. Despite evidence to the contrary, the text claims that Faraday's disc cannot be analysed with Faraday's law directly. Yes, it can!

The easiest way to see this is to not allow the path to rotate with the disc, thereby leading to $v=0$ for the complete loop. With the magnetic flux being constant, the EMF is obviously equal to zero. EMF=0, however, does not mean that there is no terminal voltage (another common and hard to disestablish misconception). Please take the definition of the EMF, seriously: EMF=0 means that (E+vxB) is compensated in the whole loop.

In our case with v=0 for the whole loop, there can be a terminal voltage, if this voltage is compensated in some other part of the loop. An observer from the laboratory frame of reference will obviously state compensation is found in the disc because there is an electric field in it. To see this, we can use the Lorentz transformation. We know that an observer sitting on the rotating disc will state E'=0. Therefore -- according to the Lorentz transformation -- E=E'-vxB=-vxB at the frame of rest. This electric field compensates for the terminal voltage.

3. Even if we allow rotation of the path, Faraday's law is still applicable to the problem.

Formal proof: We know that Faraday's disc can be analyzed using ${\text{curl}}{\vec {E}}=-{\dot {\vec {B}}}$. Since the latter is mathematically equivalent to Faraday's law owing to divB=0, Faraday's law is obviously applicable to Faraday's disc, either. q. e. d.

Explanation: The flux in Faraday's law is getting uniformly larger and larger, because the area that is surrounded by the path (a degenerated area of a solenoid) is getting larger and larger. Figure 8.4.4 in this | online book nicely visualises the area that is meant in Faraday's law and shows how it increases.

Best regards, --Michael Lenz (talk) 23:01, 25 September 2011 (UTC)

The standard definition of EMF is "EMF is the work done per unit charge traversing the circuit". With this definition, if there's no circuit, there is no such thing as EMF. See my comments above for lots of references to this definition, and also see the wikipedia article electromotive force which uses this definition and the references therein.

Let's talk about a homopolar generator in the real world--i.e., made of real metal with a nonzero resistivity. Say you short-circuit it. Then current will run through it and generate heat. Again, "EMF is work available to push a unit charge around the circuit". If charges are moving through a metal and generating heat, there is an EMF. This is conservation of energy! The heat energy did not appear out of nowhere. The heat energy is proof that there is energy available to push the electrons through the circuit.

The "counterexamples to Faraday's law" section is based closely on Feynman's Lectures On Physics, which (like most other textbooks) uses the definition "EMF is the work done per unit charge traversing the circuit" when discussing Faraday's law (or "the flux rule" as he calls it). So of course you will find the discussion confusing or wrong if you're using a different definition of EMF. :-) --Steve (talk) 03:15, 26 September 2011 (UTC)

I understand your definition of the EMF stating that "EMF is the work done per unit charge traversing the circuit". It is the definition that I use throughout the discussion. Let's look Faraday's disc with this definition in mind:

From the frame at rest, there is

• a transfer of energy into the circuit between the disc centre and the brush (mechanical energy is converted into electrical energy via the Lorentz force), and there is
• a transfer of energy out of the circuit in the load resistor (electrical energy is converted into heat)

Since both transfer rates are in equilibrum, there is no overall work done to the charge traversing the circuit, and thus, EMF=0.

I disagree with your statement that if charges are moving through a metal and generating heat, there is an EMF. You need to consider the complete loop to decide whether there is an EMF or not. According to Faraday's law, the existence of an EMF means that there is an increase in the magnetic flux. Since the magnetic flux remains constant to a large extent at Faraday's disc (the only change of magnetic flux is due to the load current; this current, however, is the consequence of operating Faraday's disc and not its cause), again, there is no EMF.

I really like Feynman as a serious author, but the examples that he showed are not sound. Not the one with Faraday's disc and probably not the other one, either. (I will analyse shortly.) Michael Lenz (talk) 22:18, 26 September 2011 (UTC)

Since you don't understand this definition of EMF, I'll give another example. An ideal AA battery has an EMF of 1.5 volts. What does that mean? It means that each electron passing through the battery has 1.5eV of usable energy (also called "available work"). The electron can use this energy in any number of ways. It can travel through a resistor and generate heat. It can travel through an LED and generate light. It can help charge up a capacitor. Etc.

Let's say we wire the battery to a resistor. Your logic seems to be: "OK, right now the battery no longer has any EMF. Its EMF just went to zero, because the battery adds 1.5eV of energy to the electron, but the resistor takes that energy away again." This isn't the right logic. Instead, you should say "The battery supplies a 1.5V EMF, and the associated energy is used to create heat in the resistor."

If you like, the resistor has a negative EMF. We don't count the EMF of the resistor as part of the EMF of the generator, because the resistor is not part of the generator. Here's another question: How much power is generated by a nuclear power plant? Maybe you say "zero, because the plant generates +1GW but the people using the power count as -1GW, and we need to add those together."

When people say "the homopolar generator has an EMF", they are not saying anything deep and subtle, they are saying something incredibly simple and obvious. You can run a television off a homopolar generator, therefore the homopolar generator has an EMF. You can hook a handheld voltmeter to a homopolar generator and read a nonzero voltage, therefore the homopolar generator has an EMF. EMF is a very simple concept if you will only relate it to your everyday life, things like reading a voltmeter or powering a television. When you're thinking about whether some EMF is nonzero, you should not start calculating integrals and changing frames of reference, you should just ask yourself one question: "Can it light a lightbulb?" If it can light a lightbulb, then it has a nonzero EMF!! --Steve (talk) 01:01, 27 September 2011 (UTC)

Electromagnetic induction without an induced current (Hering's Paradox).

Steve, I got your point. I use all these integrals and Lorentz transformations to avoid the mistakes you seem not even to be aware of. Electromagnetic induction is a mine field and certainly not anything "incredibly simple and obvious". One problem is as follows:

• If we define EMF in the way you do with the light bulb, then we cannot maintain the formulation of Faraday's law via EMF=-d/dt Phi, because it becomes incorrect.

The figure showing Hering's paradox clearly demonstrates the problem:

The observer is in the frame at rest. The permanent magnet, which I suppose to have a perfect electric conductivity and which is supposed to be (electrically) connected to the wires via the wheels, moves to the left. The area A is defined by the three wires (black) including the voltmeter and the dashed red line going through the permanent magnet but not moving with it. So everything is fixed except for the magnet. Exchange the voltmeter for a light bulb, if you want - it does not make any difference.

Analysis:

• There is an obvious change of magnetic flux in the defined area A: At the beginning when the magnet is outside the contour of area A, there is no magnetic flux. However later, when the magnet moves inside, the magnetic flux increases.
• Faraday's law states that there will be an EMF if the magnetic flux increases. So according to Faraday's law, we have an EMF. In the experiment, however, the light bulb will not shine. So, according to your light bulb definition, there is no EMF.

How do you solve this problem? I insist that this example is not one of the dubious "exceptions to Faraday's law", because up to now, I haven't seen a single exception to Faraday's law being published anywhere (Ok, I saw such publications, but the corresponding explanations were always erroneous.) Furthermore, I can explain why Hering's paradox is in perfect agreement with Faraday's law. So I suggest that you chose a sound definition of what you want to call EMF and then strictly stay with it. By now, you have three different(!) definitions with different meanings:

• EMF is defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt). This definition is not sound, because it does not tell us how fast to travel around the loop, from which frame of reference we look at the situation and if everything takes place at the same time (i. e. with the same B-field).
• Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching a voltmeter to the leads. This definition is not sound either, because it does not tell us anything about the speed at which the voltmeter is supposed to travel (E changes with the speed of the voltmeter, and so does the voltage). Take Hering's paradox as an example to see that the voltmeter does not necessarily tell you anything about the change rate of the magnetic flux, either. So again, there is an inconsistency between Faraday's law and the definition of EMF.
• $EMF=\oint \left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right){\text{d}}\mathbf {\ell }$ is well-defined and I would appreciate to take it as a definition. However, your battery/resistor example would lead to EMF=0 with this definition, so you certainly don't like it either.

As for me, I don't care which definition you choose. But I hope you got an idea about why I avoid this dubious term and why I prefer those complicated integrals instead. Furthermore, I hope that agree that there is a serious problem with the main text and try to fix it. Michael Lenz (talk) 19:39, 27 September 2011 (UTC)

I noticed that I do not distinguish well enough between the different velocities (the one of the real objects like wires, electrons etc. and the one of the contour). I still think that my calculations are all ok, but this is why we don't come to a common solution. The $v$ in Faraday's law $\oint ({\vec {E}}+{\vec {v}}\times {\vec {B}}){\text{d}}{\vec {s}}$ is always the velocity of the contour, whereas in my pictures $v$ is the velocity of the real objects. I'll change the $v$ of the integral into ${\vec {u}}$, so that we can distinguish between both. -- Michael Lenz (talk) 23:48, 28 September 2011 (UTC)

You say: "EMF is defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt). This definition is not sound, because it does not tell us how fast to travel around the loop, from which frame of reference we look at the situation and if everything takes place at the same time (i. e. with the same B-field)." Luckily, how fast to travel around the loop doesn't matter. It's the same EMF regardless. Well, I guess we want to be able to discuss "EMF at a given moment in time". So maybe we should take the limit as velocity goes to infinity. If you are pedantic and/or want to capture better what happens in reality, you can take N electrons equally spaced around the loop, and each one travels at 1 cm/s a distance L/N, where L is the length of the loop. The net effect is the same as one electron circulating once around the loop, and as N-->infinity this occurs arbitrarily quickly. What frame of reference to use? The frame of reference from which you look at the situation is the frame of reference from which you look at the situation. You say "The EMF at time t in frame-of-reference F is 1 volt". It may be different at other times and it may be different in other frames of reference. I believe this is true for any definition of EMF, right? Of course it won't matter at nonrelativistic velocities.

You say: "Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching a voltmeter to the leads. This definition is not sound either, because it does not tell us anything about the speed at which the voltmeter is supposed to travel (E changes with the speed of the voltmeter, and so does the voltage). In order to measure "EMF in frame of reference F", you should obviously use a voltmeter at rest in F. You can use twisted stretchable wires to hook a stationary voltmeter to a moving circuit. Anyways, for nonrelativistic velocities it won't matter.

You say "Take Hering's paradox as an example to see that the voltmeter does not necessarily tell you anything about the change rate of the magnetic flux, either." The voltmeter certainly does tell you exactly what the rate of change of magnetic flux is for a loop made of thin wire. Isn't this amazing? A simple relationship between two very simple things: A number on a voltmeter, and a changing magnetic flux through any thin-wire circuit in any situation you can imagine. Faraday's law is so widely used in the world because it is so simple. The cost of simplicity is that people are apt to overgeneralize it, applying it to thick conductors and not just thin wires. The best response to this situation is to tell people not to overgeneralize it, as Feynman does (among others). Your response is different: You redefine EMF and say, "EMF is a complicated concept and you cannot measure EMF with a voltmeter". That way, you make Faraday's law more widely applicable...but you also make it much much less useful!! If Faraday's law does not tell us about what a voltmeter will read for a circuit, then it seems to me that Faraday's law is pointless. You might as well forget about Faraday's law and only teach the Maxwell-Faraday equation, as Mike La Moreaux has proposed above.

To summarize: For any conceivable circuit made of thin wire, a voltmeter will tell you exactly what the change of magnetic flux is. This is a useful real-world observation and deserves a name. The name is "Faraday's law". The voltmeter does not always tell you the change of flux for circuits made of thick conductors; situations where it does not are called "counterexamples to (overgeneralized) Faraday's law" or else "reminders to not use Faraday's law for thick conductors". The advantages of this approach are: (1) This is in accord with how people use the word "EMF" in the real world, (2) This is in accord with how people apply "Faraday's law" in the real world, (3) This approach is used in mainstream textbooks (not just Feynman), (4) This probably resembles how Faraday first described the law. The "disadvantage" is that Faraday's law does not apply to thick conductors. (It usually does, but not universally.) :-) --Steve (talk) 04:14, 29 September 2011 (UTC)

I agree to most of what you say. My mistake was that I thought Faraday's law was the same as the Maxwell-Faraday equation, and I was wondering why the thin wire concept was used. Your answer is satisfactory to me. I will try to derive Faraday's law from the Maxwell-Faraday-equation, then I'll see what the exact premises are, and we can possibly add a paragraph on this. -- Michael Lenz (talk) 17:28, 29 September 2011 (UTC)

No induction?

EMF is the potential work done per electron on free electrons that traverse a path. The path need neither be closed nor conductive. There are two forms of EMF, electrostatic and non-electrostatic. The electrostatic form is just the potential difference between the ends of the path. Typically, the non-electrostatic EMF of an electrical source produces a potential difference between its terminals which powers the external circuit.

There are only two principles that are called induction: motional induction and E-field induction. The former is just a direct application of the definition of the magnetic field. The latter is given by the Maxwell-Faraday equation. The two forms of induction together include all cases. The example given for Hering's paradox produces zero EMF because neither principle of induction applies. Mike La Moreaux (talk) 19:36, 28 September 2011 (UTC)

Mike, we have ${\text{curl}}{\vec {E}}=-{\dot {\vec {B}}}\neq 0$. How can you say that there is no induction? Of course there is! -- Michael Lenz (talk) 19:56, 28 September 2011 (UTC)

Michael, that equation is incorrect. It should have a partial derivative to be the Maxwell-Faraday equation. The partial derivative disregards any flux change due to the motion of the circuit. Mike La Moreaux (talk) 21:05, 28 September 2011 (UTC)

Concerning the partial derivative: There is a dot on top of ${\vec {B}}$ indicating the time derivative (without dot: ${\vec {B}}$, with dot: ${\dot {\vec {B}}}$). Maybe your browser does not show it correctly, so I'll write $\partial /\partial t$ later on.

I think you misunderstand the meaning of motion in this context. The question is not whether the circuit, the magnet or any other object is at motion, but whether the contour line $\partial A$ that you define is at motion. According to the definition I gave for area $A$ (the three black coloured wires and the dashed red line not moving with the magnet), the area $A$ and its contour $\partial A$ are *at rest*. Imagine an observer sitting in the middle of A. At time t=0, he will not measure any significant B, because the magnet is far away. Later on, when the magnet has moved towards him, he will measure $B\neq 0$. Therefore $\partial {\vec {B}}/\partial t\neq 0$, so that there is induction. -- Michael Lenz (talk) 21:54, 28 September 2011 (UTC)

Michael, the change in flux must be an intrinsic change, that is, in the field itself, not just a change of exposure of the circuit to the field. In a case where the Maxwell-Faraday equation applies, the change in the magnetic field is accompanied by an electric field. It is this electric field which is responsible for the EMF. In the example given for Hering's paradox, there is no electric field. Mike La Moreaux (talk) 03:17, 29 September 2011 (UTC)

In the example given for Hering's paradox, there is no electric field.. Yes, there is! The electric field is located in the (ideally conducting) magnet. It can only be seen from the observer at rest, and it is compensated by the magnetic component of the Lorentz force. (Use the Lorentz transformation to be sure: An observer moving together with the magnet will measure E'=0 for the ideally conducting magnet, so the observer at rest will state E=-vxB). Best regards, --Michael Lenz (talk) 17:10, 29 September 2011 (UTC)

There is no conductor moving through a magnetic field. Therefore there is no vxB. Mike La Moreaux (talk) 19:51, 29 September 2011 (UTC)

Sure there is. The observer from the frame at rest states that 1) inside the magnet, there is a B-field, and 2) the (conducting) magnet is moving. So the magnet moves in a magnetic field -- what else? It is of no interest, if this magnetic field is generated "externally" or by the magnet itself, because there is no such thing as a movement "relativ" to the magnetic field. -- Michael Lenz (talk) 01:33, 30 September 2011 (UTC)

Where did you get the idea that there is no such thing as a movement relative to the magnetic field? It only requires relative motion between a conductor and a magnet to produce an EMF in the conductor. The conductor can be stationary and the magnet moving. It would seem to follow that the magnetic field moves with the magnet. In the example under discussion, the magnetic field moves with the conducting magnet. Mike La Moreaux (talk) 17:02, 30 September 2011 (UTC)

I understand what you mean, but you actually speak about the relative velocity between observer and magnet. If you want to define the velocity between a magnet field and an observer, you should be able to give a measurement procedure that enables the observer to measure this speed. But how, for example, would an observer be able to distinguish between a temporal change of the magnetic field and a field movement? Or - if located in a field that is constant within a certain area - how would the observer be able to measure the speed of the field, although B=const for the time span of interest?

Thus, the conception of motion relative seems quite odd to me. Furthermore, keep in mind that the field (the components perpendicular to the relative velocity of magnet and observer) change with the velocity. --Michael Lenz (talk) 09:27, 1 October 2011 (UTC) --Michael Lenz (talk) 16:52, 1 October 2011 (UTC)

You raise interesting points. According to the article on the Faraday paradox, you are correct about there being an EMF in the moving conducting magnet. I do not have any experience with this concept and do not know if it is correct. I cannot reconcile it with the working of alternators. Alternators employ a moving magnet and stationary output coils. Mike La Moreaux (talk) 01:41, 4 October 2011 (UTC)

I have now satisfied myself that there is an EMF in the moving conducting magnet. If this setup is run as a linear motor instead of as a generator it seems that it will constitute a reactionless drive, suitable for levitating and propelling a flying saucer or a spacecraft. It is very interesting as it seems to violate at least two laws of physics: Newton's third law of motion and the conservation of momentum. Mike La Moreaux (talk) 21:18, 10 October 2011 (UTC)

A homopolar motor does not violate either law. As the system gives the magnet and screw a rotational acceleration, it gives the wire and battery an equal and opposite rotational acceleration. thus conserving angular momentum. This can be easily demonstrated by hanging the homopolar motor from a string rather than holding it in your hand. Guy Macon (talk) 23:00, 10 October 2011 (UTC)

Of course, you are referring to the rotational version given in the article on the homopolar motor. In the example under discussion here, it would seem that the farther away the vertical part of the circuit at the left is away from the magnet, the less the field strength at that position would be and hence the less the reactive force would be, while the force on the magnet would be constant regardless of position. Mike La Moreaux (talk) 23:47, 10 October 2011 (UTC)

I suggest building a homopolar motor yourself, moving the wire as you describe, and seeing if your "it would seem that" happens in real life. Hint: farther away from the center of rotation also means a longer lever. Guy Macon (talk) 01:17, 11 October 2011 (UTC)

What lever? We are discussing the linear motor. Mike La Moreaux (talk) 01:24, 11 October 2011 (UTC)

If you think you can build a linear homopolar motor that demonstrates any breaking of any law of physics, go ahead. There are plenty of examples of linear homopolar motors on YouTube you can copy. Guy Macon (talk) 01:46, 11 October 2011 (UTC)

In view of the above conversation, I believe that I have come up with a proof that even the thin-wire version of Faraday's Law is false. Take a thin wire rectangular circuit and attach the pole of a permanent magnet to one side such that the lines of force are orthogonal to the plane of the circuit. Now move the circuit and magnet together rigidly in a direction perpendicular to both that side of the circuit and the lines of force. There will be a motional emf induced in that side of the circuit, but there will be no change in the flux linking the circuit. This violates Faraday's Law. Mike La Moreaux (talk) 23:44, 26 April 2012 (UTC)

There will be no change in the flux, and there will be no EMF. Therefore Faraday's law gives the correct prediction. Sure, there is motional EMF, but there is also an equal and opposite electric-field EMF (since the magnetic field B(r,t) is changing as a function of time, there has to be a curl of the electric field). Or think: If you actually built this with real wire, would any current flow? In the rest frame of the circuit + magnet, there is no EMF...so no, there cannot be any current flow. :-) --Steve (talk) 03:30, 27 April 2012 (UTC)

Very good! Obviously, I missed that. Thanks. Mike La Moreaux (talk) 22:03, 27 April 2012 (UTC)

very first equation

Shouldn't dl be written as a vector dotted with the rest? (Otherwise you end up with EMF as a vector, no?). Or is it implied dl is a vector? — Preceding unsigned comment added by 86.42.142.177 (talk) 20:54, 25 October 2011 (UTC) CHEVYTECH : I think we can agree that Faraday's Law Of Induction is not a "Primary Law". Just stating that an EMF will be generated around a closed path of a changing magnetic field does NOT explain just HOW the emd gets generated at all, it just states that it does. Faraday himself struggled with the idea of the flux "coming in from the outside" there by "cutting" the wire or conductor, where the "induced electric field" finds electrons to act on, thereby producing an "EMF" as we know it. OK, MY problem is one that is constantly used, and I think it is wrong. That is using the torroidal transformer to "prove" that flux cutting does not have to occur to induce and emf, because "the flux is contained in the core". Well, look at a torroidal transformer primary carrying a DC current. OK, all of the flux is in the core,(a MMF exists in the window airspace". There is NO INDUCED EMF, yup, all the flux is in the core, BUT there is no emf, because the flux is NOT CHANGING! When the current is increasing in the primary,(changing), waves of MMF leave the primary winding and travel thru the window space as they reach the surface of the core and reflect from the core due the the tremendous difference of permeability. As the MMF waves traverse the window, "cutting the windings in the window", they eventually enter the core, transmission like , and magnetize the core. When the primary current stops changing, MMF waves stop leaving the winding, the core is fully magnetized now, BUT the "induced EMF" occurred WHILE THE CURRENT WAS CHANGING, not after it is all established in the core.During the reverse cycle,primary current is decreasing, flux from the core, "Fall back into the place of origin, the primary winding" as MMF waves from the iron core, first put there when the primary current was changing upward in the first place. OK, FLUX CUTTING does happen in transformer, it is just a little difficult to see at first blush. In the way of experimental proof, try wrapping a wire around the leg of an energized iron core transformer,WITHOUT passing thru the window, and see how much EMF is induced. NONE, that's how much, yo have the center of a coil, well not a complete coil, but say 90% of a coil with a changin flux in the iron core and NO EMF. I will forward a website that explains all of this in much more eloquent way next post. Thank's, This is a VERY GOOD example of people still trying to get a grasp of principles that have not been fully explained or verified to everyone's satisfaction........... — Preceding unsigned comment added by Chevytech (talk • contribs) 21:38, 12 December 2011 (UTC)

Though not very popular, there are several excellent explanations on how energy transport in a transformer is achieved. If interested, have a look at the following papers:

• J. Edwards, T. K. Saha: Power flow in transformers via the poynting vector. Queensland University of Technology, 2001 Link
• F. Hermann, B. Schmidt: The poynting vector field and the energy flow within a transformer, Am. J. Phys, Vol. 54, No. 6, June 1986 Link
• William A. Newcomb: Where is the Poynting vector in an ideal transformer? Am. J. Phys., Vol. 52, No. 8, 1984, pp. 723–724 Link

Best regards, --Michael Lenz (talk) 00:57, 14 April 2012 (UTC)

Implementation (and more)

• I read the 1st line just above - its correct and should be a line integral, i.e. integral of a dot product: the line integral of force (per unit charge) around some path is the work done, and the work done (per unit charge) is the EMF induced.
• Also deleted the html (not LaTeX) "N" at the end of the very 1st eqn: what the feck is it doing there??
• Changed unpleasant "EMF" in that eqn to "script E" (LaTeX: \mathcal{E}), much cleaner.

Further changes to remainder of article:

• Add colour box to main equation
• Add physics equation navbox at the end
• Resectioned the lead, looks odd the way it is. Better to state the equation in its own section, not dribble it from the first introductory sentences

Is this ok with people? -- F = q(E + v × B) 22:26, 18 February 2012 (UTC)

There is redundancy in the 1st and 3rd/4th section:

"Faraday's law of induction says that the wire loop acquires an EMF , defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt)". The very first equation may as well be shifted down there, the Maxwell-Faraday law can be removed from section 1, and become the qualitative statement of Faraday's original explanation of the law leaving the mathematical statements for later. The colour boxes will highlight the main equations. It will render the article's approach more gentle. Hopefully this is fine also.-- F = q(E + v × B) 23:13, 18 February 2012 (UTC)

Faraday's Law of Induction is not Lorentz invariant

The Lorentz non-invariance of the Faraday's law for the moving circuit(in difference with Maxwell's differential equation for the curl of electric field, which is Lorentz-invariant, but not the same as the former) is a well-known proven fact(see, e.g. the respective paragraph of Jackson's "Classical electrodynamics" or Kholmetskii's numerous articles on the topic in question.) Which leads researchers to two alternatives: if Faraday's law is a true law of nature, then SRT is wrong; if, however, SRT is true, Faraday's law is just an empirical approximation, not a fundamental law of nature. This is the precarious position classical electrodynamics has found itself in long ago, and it is yet to be resolved. Most researchers are convinced that SRT has been proven wrong experimentally (by the FLI.) One thing is clear: noone has been able to combine Lorentz transformations and FLI (as applied to moving mathematical line or physical circuit); the problem (as well, as some serious difficulties arisen in analysis of the motion of an accelerated charge) has just been circumvented by the mainstream community of physicists, in view of the outstanding successes of classical electrodynamics and SRT and, especially, of its quantum variant. — Preceding unsigned comment added by 24.239.129.162 (talk) 23:52, 5 June 2012 (UTC)

The moving and/or deforming circuit version of Faraday's law has various forms, some of which are exact and Lorentz invariant, others of which are only approximate. The one in this article is exact and Lorentz invariant. See Faraday's law of induction#Proof of Faraday's law -- this form follows mathematically from the Lorentz force equation and Maxwell's equations. Since both of those ingredients are Lorentz invariant, so is (this form of) Faraday's law.

The version in Jackson's book, if I remember it correctly, is IMO a rather strange one: The electric field in one frame of reference is integrated at a fixed moment in a different frame of reference. With such a strange mixture of two frames, it's not surprising that it fails at relativistic velocities. The version in this article does not have that kind of thing, and does hold at relativistic velocities.

You wrote "Most researchers are convinced that SRT has been proven wrong experimentally (by the FLI.)" I doubt you seriously believe this, do you? How many professional physicists have you discussed special relativity with? --Steve (talk) 12:31, 6 June 2012 (UTC)

Voltage or Current

Gents, thank you for your dedicated discussion of the issues. Please answer a question for a simple-minded engineering physicist. Wouldn't Faraday's law predict the emf, not the current? The emf is present in free space where the field is changing. The current depends on the presence of a conductor and its impedance.

Thanks — DavidMack (talk) 22:27, 29 August 2012 (UTC)

P.S. By coincidence I notice that on the Wikipedia front page it says on this day in 1831 Michael Faraday discovered electromagnetic induction.

Yes... I take it you are complaining about the first sentence of the article? You are welcome to rewrite it but please don't make it overly technical or jargony. :-) --Steve (talk) 21:03, 30 August 2012 (UTC)

units

This article, best as I can tell, does not mention if it's in cgs, SI, or whatever kind of units. If I were fresh on my E&M I could figure it out, but this is exactly where I want to go to freshen up, and it doesn't help! — Preceding unsigned comment added by 18.111.5.181 (talk) 17:06, 9 October 2012 (UTC)

SI. I added mention in a couple places... --Steve (talk) 19:46, 10 October 2012 (UTC)

Merger with Electromagnetic induction

Although there is a subtle difference between electromagnetic induction and the Faraday's law topic (as covered here), in practice they're more than 97% the same topic, and (that's why) the electromagnetic induction article is just a stub, everything has been moved here.

We can easily cover them both with one article.

I suggest we merge them here, and further, if people agree, move the whole article back to the 'Electromagnetic induction' title, and have it cover all electromagnetic induction.GliderMaven (talk) 15:08, 16 January 2013 (UTC)

Unless I get any negative comments in the next couple of days, I will do the merge, except I'm going to merge into electromagnetic induction from here, rather than the original proposal of merging into here.GliderMaven (talk) 16:28, 21 January 2013 (UTC)

I think I'd favor moving the majority (but not all) of the information to the electromagnetic induction page. In particular, the "Applications" and the "Eddy currents" sections should be moved out, and the stuff like the history, the "two different phenomena", and the paradox sections, which might be a bit awkward in that article but are more directly tied to the actual Faraday's law, kept here. I'm not sure where the "Flux through a surface and EMF around a loop" would better fit. Unfortunately the meandering state of this article is imo largely the result of an protracted and generally opposed efforts across multiple articles involving an editor pushing his own extremely fringe view and another editor who had the habit of adding multiple examples and seemed to not understand WP:NOTTEXTBOOK. Just my two cents.— Preceding unsigned comment added by FyzixFighter (talk • contribs)

At the moment, the electromagnetic induction article contains only Faraday's law, whereas Faraday's law contains the whole of electromagnetic induction.

This is clearly, at best, backwards.GliderMaven (talk) 15:14, 22 January 2013 (UTC)

Because electromagnetic induction is a superset of Faraday's law, the flux/emf thing would fit in there just fine, whereas, as you note it is more or less off-topic and meandering in an article putatively only about Faraday's law.

So I agree with you, and find that these issues would be fixed by a proper merge.GliderMaven (talk) 15:14, 22 January 2013 (UTC)

As long as it's a reorganization of material, leaving this article with the info that is more strictly Faraday's law related, rather than a complete merge into a single article, I can support it. Looking again at the TOC, I would say most of the information in sections 1-3,5-7 should stay here and be improved. --FyzixFighter (talk) 16:11, 22 January 2013 (UTC)

I'd agree, that that is a reasonable way to go, particularly if I look only at this article. However, I invite you to read the electromagnetic induction article, which is frankly a total embarrassment, and try to explain to me what could be done with it. It seems to me at least that an article that only subarticles another article is de facto a content fork. To make it into a comprehensive and comprehensible stand alone article, because of the nature of the material we are trying to shoe-horn into articles, I cannot see any good way to do that, other than merge it.GliderMaven (talk) 22:23, 22 January 2013 (UTC)

Ok, so I did the merge, I hope you find what I've done acceptable in spite of your misgivings. I moved the section 4 you indicated to the end, since it points outwards to Special Relativity. It's unclear to me that it should be in the article, but it didn't seem entirely right to take it out, but I think the article flows better, and is better scoped. I also pointed the Faraday-Maxwell equation to the relevant section rather than to Maxwell's equations to give it better context and numerous other things.GliderMaven (talk) 22:40, 24 January 2013 (UTC)

Unmerge proposal

Faraday's law of induction is one of the most important laws of Electromagnetism. I think it should have its own article. Martin Hogbin (talk) 18:06, 3 March 2014 (UTC)

I'd be for unmerging. I'm still a little surprised the article got merged completely in the first place given the previous concerns that I had voiced in the previous section. Looking at the article before the odd merge a year ago, the lede would need to fleshed out and I'd say only keep the material in sections 1-3, 5-7 which can then be expanded/whittled down as needed. --FyzixFighter (talk) 18:37, 3 March 2014 (UTC)

Yes, Faraday's law is a mathematical law concerning rate of change of a magnetic field and induced emf. Electromagnetic induction is a more general subject, covering self-inductance (which was independently discovered by Henry) for example. general practice now seems to be to name laws after their discoverers and Faraday's is pretty fundamental to physics.

I will put a notice on the Electromagnetic induction page about demerging and if there is no objection, I suggest that we do it. Martin Hogbin (talk) 11:33, 4 March 2014 (UTC)

Does not Faraday's law of induction cover self inductance? I thought it applied to all cases where there is no motion.Constant314 (talk) 17:34, 7 June 2014 (UTC)

Examples: Generators

I just noticed that generators are listed as an example. But generators use the other form of induction that arises from a moving conductor.Constant314 (talk) 18:26, 8 June 2014 (UTC)

I think that some generators have a spinning magnet and stationary conductor, and others have a stationary magnet and spinning conductor. I could be wrong. --Steve (talk) 11:47, 9 June 2014 (UTC)

I had not thought of that. It would seem that there would probably be less moving mass if the dc field was on the rotor.Constant314 (talk) 17:56, 9 June 2014 (UTC)

"Counterexamples" gallery

The one thing missing from counterexamples gallery is switched circuits. Feynman in discussing the rocking plates notes: "When the material of the circuit is changing, we must return to the basic laws. The following switching example is due to the late emeritus professor W. J. Hooper of Principia college and I have drawn it based on the rocking plates in three images for animation.

http://www.mrk-inc.com/users/bspam/Faraday01.bmp

http://www.mrk-inc.com/users/bspam/Faraday02.bmp

http://www.mrk-inc.com/users/bspam/Faraday03.bmp

Generally I am not a fan of animation. It is too distracting. Of course there are some things that are vastly more understandable if animated. But if you have just three pictures then combine them into one picture and post it like that. But not a BMP or JPG.Constant314 (talk) 22:41, 8 January 2015 (UTC)

Indeed this switched circuit explains the rocking plates as they really represent a switching from one path through the plates to the next as the plates rock.

However, I am not practiced enough with the Wikipedia editor to add such images to the gallery or animate the three images into a single animation. Therefore if anyone finds this example of value, help in adding it to the article is needed. Thanks. 68.75.26.150 (talk) 10:04, 8 January 2015 (UTC)

That's nice! Hmm, my personal opinion is that two examples is already sufficient to make the point, and adding a third example would be unnecessary and excessive (i.e. it would make the section too wordy). But I don't feel very strongly; I don't really mind if someone adds it.

Wikipedia doesn't have any tools to turn a set of images into animated gifs. You have to do it yourself, using photobie or imagemagick or photoshop or http://gifmaker.me/ or whatever. --Steve (talk) 15:36, 8 January 2015 (UTC)

It has always seemed to me that the rocking plates is an impure example. It is a continuous destruction of one circuit followed be the construction of a different circuit and that should generate no EMF, but the material of the plates does move and when it does it drags electrons with it so there ought to be a little bit of EMF, though a lot less than you would get by naively applying FLI. I suppose by changing the radius of the plates and the pivoting point, you could make it arbitrarily low.Constant314 (talk) 22:38, 8 January 2015 (UTC)

Avoiding the perpetuation of falsehoods

"Faraday's law of induction is a basic law of electromagnetism predicting how a magnetic field will interact with an electric circuit to produce an electromotive force (EMF)—a phenomenon called electromagnetic induction." The very first statement on this page is problematic, because it is technically incorrect. The term EMF as an abbreviation for electromotive force is archaic, but this is not really an issue. The issue here, and with almost every treatment of this subject, is the assumption that there is a causal relationship between a changing magnetic field and an "induced" electric field, or vice versa. An electromotive force does exist because an electric field is induced, but it is not the changing magnetic field that causes it. Jefimenko's equations (general causal solutions to Maxwell's equations) make this explicitly clear. Both electric and magnetic fields arise from charge density and current density, and neither are dependent upon the other. Simply providing a link to the Wikipedia article entitled "Jefimenko's equations" and providing a brief explanation might be sufficient. The following reference may be of interest: Rephrasing Faraday's Law http://bulldog2.redlands.edu/fac/eric_hill/Research/Rephrasing%20Faraday's%20Law.pdf Rygard1 (talk) 17:05, 10 March 2015 (UTC)

There is always room for a good write up on a new explanation providing there are proper reliable sources, but this is an encyclopedia and not the arbiter of truth. That the law of induction says what it says is a historical fact. Whether it is cause and effect or effect and effect or mere mathematical artifice to represent the effects of non-local charges and currents it does not matter. It is used the way it is used and the encyclopedia reflects that.Constant314 (talk) 21:08, 10 March 2015 (UTC)

The article does not say that the magnetic field "causes" an EMF, does it? It describes the circumstance under which an EMF arises, in a way that I believe is technically correct. If you disagree I'm happy to change the wording slightly. For example: "Faraday's law of induction is a basic law of electromagnetism predicting that an electric circuit in a magnetic field experiences an electromagnetic force (EMF) when the magnetic field changes, or when the circuit moves or deforms." Would that help?

I don't understand your "archaic" complaint. Do you believe that people have generally stopped abbreviating "electromotive force" as "EMF"? This is not consistent with my own experience. Can you be more specific? Like, what is your profession? Or where did you hear this?

Even though I am happy to rephrase the intro to avoid implying a cause-and-effect relationship, I do want to say that I disagree with the S. Eric Hill article (and other articles like it, I've seen one other). I actually had a long debate with someone about this before, see [1].

Think about this: In the whole history of electromagnetism from the 19th century until 2010 (when that S. Eric Hill article was published), not one person in the world has designed a faulty transformer or antenna, nor even lost a single point on a single homework problem, from their mistaken belief that a changing magnetic field can cause an EMF. Now, I happen to think that this fact should tell us something important: It should tell us that a physics-based analysis of cause and effect, like S. Eric Hill's, is not useful. But understanding cause-and-effect is obviously essential in any engineering design! How can that be? The answer is: The way people think about cause and effect in the real world is more subtle and complex than can be captured by any purely physics-based argument (like S. Eric Hill's).

Here is an example: Talk to an expert analog circuit designer. When a resistor is driven by a current source, she will have no problem saying "there is a current through this resistor, which causes a voltage drop across it". When a resistor is driven by a voltage source, she will have no problem saying "there is a voltage drop across this resistor, which causes a current to flow through it". In a physics-based analysis, these cannot both be true. But she nevertheless uses this understanding to expertly design circuits, and she would be handicapped if we forbade her from making those types of statements. What she is doing is describing logical relations, not physical ones. Context matters, intention matters. This is the way people really use cause-and-effect thinking. S. Eric Hill wants to forbid people from ever thinking that a changing magnetic field causes an electric field. This is a handicap, just as in the example above. A purely physics-based cause-and-effect analysis is ultimately misleading, even if it's technically correct. The reason is, it is starting from a mediocre definition of "cause and effect", one that is quite different than how people use the term "cause and effect" intuitively in their everyday lives. --Steve (talk) 21:30, 10 March 2015 (UTC)

Cause and effect no longer really have any place in physics. Martin Hogbin (talk) 22:48, 11 March 2015 (UTC)