Talk:Derivative/Archive 1

Archive 1

Archive 2

Archive 3

Funny

funny trying to define "derivative" without used the phrase "derived from"??

--(talk)BozMo 19:58, 15 May 2004 (UTC)

Why is the "references" section pointing to a wikipedia link which is obviously a shameless plug on someone's book?

Terminology

Is there a name for the function of which a derivative is being taken? I want to say "differand" (the operand of a differential operator, like "integrand" for integration) but cannot find a reference anywhere online or in the books I have on hand.

"differend" has a [meaning] quite apart from maths, due to Jean-François Lyotard

I'm now using "derivand" after discussing it with some friends.

Where derivatives don't exist...

"Functions do not have derivatives at pointdiscontinuity." Not entirely true... derivatives also don't exist at points where the function isn't smooth i.e. f(x)=|x| at x=0.

do agree with this fact. puttig it more precisely a function is not diferentiable at "pin" points. this is because first derivative is nothing but the slope of the tangent at that point. to have a tangent at a point u need to have a curveshape . i.e. a radius of cuvature should exist at that point. so if we a have pin point that is a sharp point like |x| at x = 0, we don't have any radius of curvature at that point and hence can't be differentiable. this is about the significance of the differentiability.

The point where the derivative does not exist is called a cusp. --justinphd

Critical Numbers

I believe that a critical number of f(x) also happens when f '(x) is undefined, not only when it is equal to zero.

I second that.

GTBacchus 05:21, 2 Dec 2004 (UTC)

deleted sentence

From the secion "Using Derivatives to Graph Functions":

"Additionally, the supremum of a continuous function on an open and bounded domain will also be one of the local maxima; the infimum will be one of the local minima--this gives one an easy way to find the bounds of the function's range."

I'm deleting this sentence. Counterexample: the function e^x on the open interval (0,1). Its supremum is e and its infimum is 1, but neither is a critical point.

Neither is a critical point, but both are local extrema, right? so how does that contradict the sentence? -Lethe | Talk 19:00, Jan 8, 2005 (UTC)

It's probably better to correct the sentence than delete it. --Elektron 16:23, 2004 Jun 30 (UTC)

If you can correct that sentence without making it 3 times longer, go for it. GTBacchus 18:00, 2 Jul 2004 (UTC)

f prime

On my computer, f prime looked like an f. If I looked really close, I could tell that the f that was really an f prime had a more rounded top than an f that wasn't prime. But anybody who can't read fine print any better than my wife can't see that, and the rest of us wouldn't notice either if we weren't expecting it. Maybe other people's fonts don't have that problem, but all I can do is fix the problem I can see here.

So I put a space between the f and the prime. It doesn't look perfect - the prime is more lost with an f than it is with a g - but at least it won't cause a computation error.

Putting a space between the f and the prime doesn't work when the formula is inside those <mmath> thingies (mmath mispelling intentional to prevent it from formatting my text) in the Algebraic Manipulation section. But most of the formulas look the same with or without the <mmath> thingies. So I took them off in many places. But not in all places, because exponents don't work without the <mmath>'s. My conclusion was to take off some of the <mmath>'s but not all of them. The result is even more funny looking than the f prime/g prime problem, but at least it won't cause a computation error like the previous version would have. Art LaPella 06:49, Sep 2, 2004 (UTC)

Since then I reported the problem as a bug, and got this answer: "This is a problem with the specific fonts your browser is displaying and has nothing to do with MediaWiki or the site configuration." That's imaginable, except I don't know enough to monkey with fonts, so many of you may have the same problem. On my wife's computer f prime doesn't look like an f, but it looks like f square, which is almost as bad. Look at prime (symbol) and see if the f prime looks like an f. If so, Wikipedia presumably has lots of f primes that look like f's. Art LaPella 20:14, Sep 2, 2004 (UTC)

That's definitely your browser's choice of fonts. Pick a different font. On OSX, the prime is too low (the top of the prime is below the top of the f), but otherwise it's fine. If I change the font to Times, the italic f is too italic so the prime is stuck to it. This is a problem with OSX's renderer (though properly aligning italic text beside normal text has always been a problem). Either way, catering for rendering bugs isn't a good habit to get into. Elektron 13:35, 2004 Nov 1 (UTC)

Of course, we could change it back to an italic apostrophe, which probably renders more correctly but is even more incorrect (in Unicode, anyway). Elektron 13:41, 2004 Nov 1 (UTC)

Wouldn't it make sense to put the math tags back in, and display math as a PNG for those who have problems? I suspect Art LaPella would have to do this manually for his user, or move "formulas that have primes" to the category of formulas which should use PNGs by default (which the WikiMedia people may be reluctant to do), but that makes (IMHO) more sense than violating Unicode and WikiMedia standards for the benefit of someone with a poor choice of fonts (which may be a poor choice on the part of whoever developed the browser, I'm not blaming anyone, it just doesn't seem to matter to me). Roie m 12:18, 2 Dec 2004 (UTC)

Does this all mean it works with your choice of a font, or does it mean you looked until you found a good one? I looked at several computers belonging to neighbors and friends and ALL of them show f prime as f or as f box. I don't see why it matters that I could pick a different font or browser - I've already learned calculus anyway, but anyone who hasn't will be as hopelessly confused as a kid with an arithmetic book whose + looks like a -. They won't stop to try a different font, they will just get the wrong answer. Software that works for a minority that knows the trick, is software that doesn't work. If there is no high tech solution, a space before the prime works fine. Art LaPella 63.229.19.235 23:25, 12 Apr 2005 (UTC)

Ambiguous statement

One should charitably assume that the statement

"Functions do not have derivatives at points where they have either a vertical tangent or a discontinuity."

means that if a Function has a discontinuity or a vertical tangent then it is not differentiable; the converse of course is false. Shouldn't this be made clearer, since many readers are likely to be much less eager to rely on principles of charity.

Also could the word "embodies" used in the phrase

"a derivative embodies in terms of mathematics a rate of change"

occuring in the introduction be be replaced by something indicating more precisely the relation between the derivative and the rate of change? CSTAR 01:20, 8 Jan 2005 (UTC)

The alternative difference quotient

What exactly does this section add? Wouldn't it be enough to say that the derivative of f at c is also the same as

$\lim _{x\rightarrow c}{\frac {f(x)-f(c)}{x-c}}.$

CSTAR 05:57, 8 Jan 2005 (UTC)

slope of parametric functions

the rule that dy/dx = dy/dt / dx/dt for parametric functions seems like a useful formula to me. Sure, it's redundant, because it can be derived from the Chain rule, but so derivatives for inverse functions and implicit differentiation. If derivatives of parametric functions are redundant and have to be deleted, then shouldn't these other be deleted as well? I believe they all have a place here and should stay. -Lethe | Talk 22:47, Feb 6, 2005 (UTC)

also, the quotient rule follows from the product rule and the power rule. In fact all the rules follow from the definition. So a better criterion for listing a rule than "is it independent?" is the criterion "is it useful?". Lethe | Talk 23:05, Feb 6, 2005 (UTC)

You have a point. If you want you can put it back. But could you please not make it again into an ugly red link which will never be filled (or do write an article on that, and put a short blue link). Also, it was somewhat misleading to call those things variables, they were functions.

In other words, that thing is indeed somewhat reduntant, so if it there at all, it should be correct and look good. What do you think? Oleg Alexandrov 23:10, 6 Feb 2005 (UTC)

I think I would like to include the formula for the slope of a function in polar coordinates, and underneath that rule would be the perfect place to put it. No? -Lethe | Talk 00:15, Feb 7, 2005 (UTC)

You mean, you want the formula for polar coordinates in the Algebraic manipulation" section? If so, I think that would be too much detail for the scope of that section, as it deals with formal differentiation rules. Maybe you could write another section, or even better a new article, describing how to apply and interpret these differentiation rules in more concrete settings, as the polar coordinates, implicit functions, etc. Oleg Alexandrov 00:30, 7 Feb 2005 (UTC)

Well.. OK, maybe it doesn't belong in there. But I'm skeptical about it deserving a whole article. -Lethe | Talk 01:25, Feb 7, 2005 (UTC)

I agree it does not deserve a new article. And I agree with you, more things could be said about differentiation rules. But probably it is good to leave things the way they are, this article is already quite long. Oleg Alexandrov 01:50, 7 Feb 2005 (UTC)

Some pictures

I think we need some good graphics in this article. I'm pretty proficient at XFIG and will be happy to make them IF I get suggestions of what might be useful; I'm getting tired of being mired in a controversy :) CSTAR 23:49, 6 Feb 2005 (UTC)

Hey CSTAR, I noticed several times you use the title of the previous section as subject for your current post, that can be confusing :)

About pictures. The section "Using derivatives to graph functions" could use a nice picture I think. I don't have other suggestions. If you don't want to get mired in a controversy again, maybe you could suggest what you want to graph, and then we can discuss if this is a good idea. :)

PS So are you claiming somebody got mad at your graphics? Did you graph naked women or something? :) Oleg Alexandrov 23:55, 6 Feb 2005 (UTC)

I'll bet CSTAR is talking about the goings-on in Bell's theorem and related pages. I doubt we will be able to stir up too much controversy about graphs of functions over here. -Lethe | Talk 00:10, Feb 7, 2005 (UTC)

Yep.CSTAR 00:12, 7 Feb 2005 (UTC)

Suggestions for pictures

I propose initially at least three illustrations:

1. One similar to the picture illustrating the secant that is already there

2. One picture illustrating the tangent

3. One picture illustrating the tangent as a limit of secant

These illustrations would all be in the same style and moreover, new ones could be easily produced from the XFIG sources.

Other possible pictures include

• illustration of

${\frac {\Delta y}{\Delta x}}$

• illustration of convexity and concavity.

CSTAR 03:04, 7 Feb 2005 (UTC)

I think the first three should be good idea. The one about convexity and concavity, that is badly needed on the Convex page. I am not sure about the last one, ${\frac {\Delta y}{\Delta x}}$. Oleg Alexandrov 04:25, 7 Feb 2005 (UTC)

Non-integer nth derivative -- is it possible?

Just out of curiosity, is there any such thing as an nth derivative for non-integer values of n? Fredrik | talk 21:11, 7 Feb 2005 (UTC)

The short answer is yes. The long answer is that I don't know exactly how it is defined. It might have something to do with taking the Fourier transform, then multiplying by $x^{\beta }$ where $\beta$ is the n thing you want, then taking the inverse Fourier transform.

I think one need some care in defining this kind of derivative, as it might be not unique (like the indefinite integrals).

Other people might know more. Oleg Alexandrov 21:22, 7 Feb 2005 (UTC)

This is a simple application of the functional calculus for self-adjoint operators. CSTAR 21:23, 7 Feb 2005 (UTC)

Sorry, no simple answer to how to generalize derivatives. But yes, it is possible. Oleg Alexandrov 21:45, 7 Feb 2005 (UTC)

I'll accept the short answer for now, then. Thanks. - Fredrik | talk 23:17, 7 Feb 2005 (UTC)

for more, see fractional calculus and differintegral -Lethe | Talk 23:41, Feb 7, 2005 (UTC)

Excellent; the article on fractional calculus seems digestible. Fredrik | talk 08:33, 8 Feb 2005 (UTC)

I can especially recommend the fractional calculus article, as it also will introduce you to the wonderful Cauchy formula for a function...which in turn is directly related to how to understand Feynamn diagrammes....

Example of pictures

Here are some examples. I have the xfig sources, so changes are easy.

(Deleted)

Nice pictures! Just several remarks.

1) Arrows could be made bigger (much bigger).

2) The axes could be made thinner. This so that the more important parts of the image are the thicker ones, and the more secondary ones be thinner.

3) It is good if the pictures are displayed at the natural resolution at which they were created. Otherwise things look blurry/or pixelated. So, could you make the images smaller, make sure they are not aliased, and then remove the thumb:300px thing. That would be great. Thanks! Oleg Alexandrov 21:44, 7 Feb 2005 (UTC)

PS Are you thinking of making some pics for the convex page too? Oleg Alexandrov 21:44, 7 Feb 2005 (UTC) --

"It is good if the pictures are displayed at the natural resolution at which they were created."

Unfortunately, this doesn't seem to work as you suggested. Maybe another drawing program might work better, but xfig is a standard GNU utility with no copyright problems. However, I did redraw the illustrations taking into account your other suggestions. I will upload them within the next day or so so you can have a look.CSTAR 23:48, 8 Feb 2005 (UTC)

Those were just suggestions, ultimately you are in charge of how the pictures will look. About the natural resolution, what worked for me, was to save the pictures as .eps, open them in gimp at high resolution and putting a checkmark on the "antialias" check box, then scale them to proper size and export as png. But most likely this is not necessary. The pictures look just fine the way you showed them. Oleg Alexandrov 00:10, 9 Feb 2005 (UTC)

PS I did follow the Bell-CT show recently (I hope she does not see this page :) I believe nothing will convince her to back off. (She is even proud of that scientist's comment which did not have good words for her work :) Oleg Alexandrov 00:10, 9 Feb 2005 (UTC)

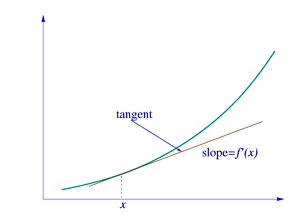
CSTAR 05:31, 10 Feb 2005 (UTC)

Awesome! Looking forward to seeing these on the main page. Oleg Alexandrov 05:51, 10 Feb 2005 (UTC)

Thanks! BTW it's nice to get some ---- "validation". Not "you're ignorant and have minimal qualifications to draw pictures" :)

CSTAR 06:05, 10 Feb 2005 (UTC)

Well, you do have minimal qualifications to draw pictures.

Note, this is not an offence. Having minimal qualifications means you have a lower bound. As far as the upper bound, the sky's the limit. :)

Good job! Oleg Alexandrov 06:09, 10 Feb 2005 (UTC)

Red links in the references

At the end of the article, one has the following reference

• Larson, Ron, Hostetler, Robert P. and Edwards, Bruce H. (2003). Calculus of a Single Variable: Early Transcendental Functions (3rd Edition). Houghton Mifflin Company. ISBN 061822307X textbook site online

Now, I have nothing against making red links which one day will become articles. However, I really doubt the links above will ever be filled, and if yes, if those will be good articles. After all, we are talking about a textbook among many.

Note that the link to Larson, Ron is not red, but all that article actually says is that Ron Larson wrote the Calculus of a Single Variable: Early Transcendental Functions book, plus another one; and who the editor is. And I doubt that guy did anything else as remarkable as to be worth writing in here.

I would say the links in that reference are reduntant. What do you think? Oleg Alexandrov 15:52, 13 Feb 2005 (UTC)

Agree. Obliterate the links. Maybe the Ron Larsen article should be on the VfD list also? CSTAR 16:10, 13 Feb 2005 (UTC)

I agree on the VfD thing. Let us see what others have to say. Oleg Alexandrov 17:05, 13 Feb 2005 (UTC)

I agree. Lethe | Talk 20:03, Feb 13, 2005 (UTC)

Well, I will VfD that one then. Oleg Alexandrov 20:48, 13 Feb 2005 (UTC)

How to differentiate a matrix by a matrix?

(by User:Freshwind)

I don't think that's possible. Oleg Alexandrov 04:13, 26 Feb 2005 (UTC)

Hmm.. I think maybe it is possible, at least at the level of physical rigour. I seem to remember seeing my QM prof doing it to get from Hamilton's equations of motion to Heisenberg's equations of motion. On the other hand, I've never seen it at home across the street in the math department. So... hm.. -Lethe | Talk 04:42, Feb 26, 2005 (UTC)

Actually I take it back. The derivative can be defined in any Banach space, so of course you can differentiate in respect to a matrix. If the function f is defined on some open set of matrices, taking values in another set of matrices, say like X→X² then its derivative will be a linear function from one set of matrices to antother set of matrices.

This is not a simple answer, but I don't think a simple answer exists. Oleg Alexandrov 05:34, 26 Feb 2005 (UTC)

The definition I remember from the class was something along the lines of

$\lim _{\epsilon \to 0}{\frac {f(x+\epsilon I)-f(x)}{\epsilon }}$

where I is the identity. This doesn't seem like a great definition to me. I'm not sure whether I'm remembering it correctly, because this definition seems to in some sense be only a derivative in the "identity direction", if you know what I mean. Your observation about Banach spaces is great, I should have thought of that. But what norm will you use on the matrices? Will the answer depend on that choice? -Lethe | Talk 07:50, Feb 26, 2005 (UTC)

The answer will not depend on the matrix norm (they are all equivalent anyway). Above, instead of I anything can be put. The problem is though, that the derivative of X^2 at X will no longer be 2X, rather some linear transformation, or if you wish, some other matrix in a larger space. Oleg Alexandrov 09:42, 26 Feb 2005 (UTC)

firstly, you claim that the definition of the Banach space derivative won't depend on my choice of norm. I agree with that, and should have known, right? All norms are equivalent for finite dimensional spaces.

I don't follow your comment about the funny definition I listed. Firstly, sure, I could choose another "direction" along which to take the derivative than I. but how do I choose? and presumably the answer will depend on that choice?

Is that definition even a sensible definition? Why do you think it won't give 2X for the derivative of X^2. I am sure that it will give that derivative. In fact, the proof can be taken wholesale from the real valued example. But it can't be the same as the Banach space derivative, since it doesn't use a norm in its definition. So there must be something wrong with it. Another reason that mine is different from the Banach derivative is that my derivative is a (not necessarily linear) function between two matrix spaces. For example, using my derivative, a function x |-> e^ax is a map from nxn matrices to nxn matrices. You can take the derivative of it and get a new map, x |-> ae^ax. The Banach space derivative is different, it gives you instead the linearization of the function at each point. Are the two related? Hm -Lethe | Talk 12:14, Feb 26, 2005 (UTC)

One could call your non-norm dependent derivative a "weak derivative" maybe?

Why do you think it won't give 2X for the derivative of X^2.

X and the increment are non commuting! That messes things up. (E.g. the Campbell-Hausdorff-Baker formula for exponentiation.)

CSTAR 17:02, 26 Feb 2005 (UTC)

OK, sure, I see that. I meant if I use the identity for my increment, then there should be no issues about commutativity. But rereading Oleg's comment, I see that must be what he had in mind. Lethe | Talk 23:05, Feb 26, 2005 (UTC)

PS, I have really run out of steam with the Bell's theorem stuff. I'm no longer keeping up with edits and talk pages. I am glad to see Pjacobi doing something though.

We'll see where that goes.CSTAR 05:05, 27 Feb 2005 (UTC)

OK, let me make myself rigurous.

Let V=M(2, 2, R) be the space of all matrices with real coefficients and size 2 by 2. Let f:V→V be the function f(X)=X² which is a nice-looking function, it just squares a matrix. Let A be a point in V. The derivative of f at A is a linear transformation L:V→V such that

$\lim _{\epsilon \to 0}{\frac {f(A+\epsilon Y)-f(A)}{\epsilon }}=L(Y)$

for any Y a 2 by 2 matrix. Here, choosing Y means choosing a direction going from A. By using the above formula, the addition and multiplication properties of matrices, and the fact that the matrices don't commute, the expression for the derivative of f at A becomes

L(Y)=AY+YA

which, as expected, is a well-defined linear map from V to V, as a respectable derivative must be. I hope this is a bit clearer now. Oleg Alexandrov 17:08, 26 Feb 2005 (UTC)

Firstly, nothing we have done requires 2x2 matrices, only a multiplication. Let's work in a generic Banach algebra instead.

Secondly, I notice that if you had chosen instead the map $X\mapsto X^{3}$, it seems that our "weak" derivative at X in the Y direction will be $X\mapsto X^{2}Y+XYX+YX^{2}$ which is not linear in X. But actually, we only require that our derivative be linear in its other argument, the direction argument, not in its "base point" argument. So we're still respectable.

Thirdly, your notation is very suggestive of the Lie derivative. And now that you've put that suggestion in my head, I do see that this derivative has a very similar definition. I wonder if this thing really is a Lie derivative.

Finally, I was going to ask for a comparison between our "weak" derivative and the Banach space derivative. In the Banach algebra, I check that the Banach derivatives are the same as the "weak" derivatives. Does that mean that this weak derivative is a more general object? Agrees with the Banach derivative in Banach spaces, but can also be defined in any algebra?

Of course it doesn't mean that. I get it now. This thing that we're calling the "weak" derivative does not actualy exist. You can't take limits in just any old algebraic structure, you need some way of turning your objects into real numbers for an ε-δ limit, which the norm provides, or at least a topology, which the norm provides. The formula I gave above simply has no meaning, or rather, it provides the intuitive heuristic idea behind the rigorous Banach derivative. So I'm glad that in my original comment, I included the proviso "up to the level of physical rigor".

Well, you can use a weak topology for that I guess. But my knees might get weak.CSTAR 05:05, 27 Feb 2005 (UTC)

And now that I've come to the realization that this "weak" derivative does not exist, I think my musings about its relation to the Lie derivative are weak at best. Your last reply helped a lot, Oleg, but it was really only when I was writing my followup questions that the whole thing crystalized for me. Do you agree with my conclusions? -Lethe | Talk 23:05, Feb 26, 2005 (UTC)

I agree with your conclussions, at least with the ones I understand. If you talk about spaces which are not Banach, my knees get weak, and I faint! Oleg Alexandrov 23:37, 26 Feb 2005 (UTC)

Matrix multiplication is smooth so matrix groups are Lie groups. Any smooth function between Lie groups has a derivative: its tangent map between the corresponding Lie algebras. This is not the Lie derivative.--MarSch 28 June 2005 13:13 (UTC)

there is no definition

This (should-be important) page does not respect the guidelines of Wikipedia:How to write a Wikipedia article on Mathematics : there is no "Definition" section and no precise definition of the terms used.

Also, part of the article only refers to derivatives of functions of one real variable and/or taking values in R, without this being mentioned.

It is not said if the point where the derivative is taken must lie in the interior of the function's domain or if it can be at the border. (Of course, if there is not even a definition...)

Once again, I plead in favour of adopting the rule that an article starting with "in mathematics" should, no: must have a rigourous and at the same time, general definition, before, not "maybe after", handwaving explanations, historical facts (which of course are important) and things like that. — MFH: Talk 20:32, 24 May 2005 (UTC)

I add my voice to the above comment. I am concerned that there is insufficient emphasis of the idea that this article discusses the derivative of a real-valued function defined on real numbers.

On the other hand, putting in too many qualifiers and strange symbols like R in the introduction may turn people off. After all, the vast majority of people who have a passing familiarity with the concept of "function" in mathematics probably think only of such R-valued functions on R (and probably without even realising that's what they're thinking of). I'm not sure of what the best way to handle this is. Dmharvey File:User dmharvey sig.png Talk 00:45, 26 Jun 2005 (UTC)

Stop complaining, and get busy writing! -Lethe | Talk 03:05, Jun 26, 2005 (UTC)

some of us are reading the stuff because we do not yet know it and so are hardly qualified to write about it. in that light, i would like to add a complaint: the notation for second (and higher) derivatives is introduced without explaining what a second derivative actually is.

Just don't make it as perfectly precise that it stops being understandandable to non-mathematicians. Oleg Alexandrov 03:42, 26 Jun 2005 (UTC)

Scope of derivative article

Hi Oleg, I'm wondering if you have any other suggestions about how to deal with my question about the scope of the derivative article. As it stands, I feel the introductory section is inaccurate. For example, where it says "It should be noted that not all functions have derivatives", clearly this phrase is not intended to apply to the function which assigns to each set its power set (!).

I think implicit here was the assumption that all the functions talked about are of one real variable with real values, an assumption which I don't find unreasonable. Oleg Alexandrov 21:17, 26 Jun 2005 (UTC)

I think it is important to qualify the scope of the article at the beginning, in some way that does not turn off people who were expecting only functions of real numbers (or who know no other kind), while still remaining accurate. I had hoped some kind of comment like the one I had added would do this. Thanks. Dmharvey File:User dmharvey sig.png Talk 16:03, 26 Jun 2005 (UTC)

Well, you see, all the concepts of derivative (directional derivative etc), ultimately came from the lowly one variable derivative. I find nothing wrong with the current article layout where things are written in the increasing order of complexity, in historic order, and that the introduction at the level of undergraduates. I wonder what others think. Oleg Alexandrov 21:17, 26 Jun 2005 (UTC)

Maybe a derivative (generalizations) article or disambiguation page could be written, and a (short) link to it put at the top? Oleg Alexandrov 21:20, 26 Jun 2005 (UTC)

I side on Oleg Alexandrov.--CSTAR 22:01, 26 Jun 2005 (UTC)

OK, I agree that Oleg's suggestion (e.g. a derivative (generalizations) page) would be an improvement, but I still don't think it addresses the real issue.

The problem is that this is an encyclopaedia article, not an introductory chapter or preface of a high school calculus textbook. I don't have any problem with WP having an article about the derivative, with the same material and aimed at the same audience as the present version of the article. In fact I think it's an excellent idea to have such an article. However, it should be called something like Derivative (high school version) (or preferably a more tactful title), and the main derivative article should prominently link to it, labelled in such a way that a high school or college student will find it without any hassle.

The present state of the article is a bit like having an article on group theory that only discusses permutation groups, or an article on manifolds that only discusses submanifolds of Rⁿ, simply because it's easier, more elementary, and closer to the order that things happened historically. I don't think that's what WP should be about. Of course I don't expect group theory to cover everything about groups; but it certainly should give some immediate indication of the scope of the concept. At the very least, if it's only going to discuss permutation groups, it should plainly mention the fact that this is only one way of looking at groups, and there is more to the story; and it certainly should not define a group to be what amounts to a permutation group. Similarly for derivative.

Dmharvey File:User dmharvey sig.png Talk 22:27, 26 Jun 2005 (UTC)

I agree with Dmharvey. Correctness and completeness should take precedence over approachability in an encyclopedia. -Lethe | Talk 04:19, Jun 27, 2005 (UTC)

Actually, I don't think correctness and completeness should take precedence over approachability. We simply must have all three, to the maximum extent possible. I strongly believe this is always possible to do. Dmharvey File:User dmharvey sig.png Talk 28 June 2005 14:20 (UTC)

Hmm. I don't think anyone is arguing that the article should not be correct. But the remarks at the beginning of the article currently, are correct, are certainly informative to anyone not knowing anything about calculus (say a 10-year old) and do not preclude having some pointer to calculus on Banach manifolds.--CSTAR 04:27, 27 Jun 2005 (UTC)

I agree strongly with harvey and lethe. The intro is too sloppy. This stuff shouldn't be in the intro at all I think. The intro should be intuitive. But that is very different from sloppily formal. It should talk about drawing a curve on a sheet of paper and then touching straight lines to it or something. THAT is intuitive but not sloppy. I also disagree with any suggestions for splitting so far. They imply that there is no problem with this article and that is simply not the case.--MarSch 28 June 2005 12:44 (UTC)

Reply

The problem is that this is an encyclopaedia article, not an introductory chapter or preface of a high school calculus textbook.

Good point, but I think it's only valid if you understand encyclopedic in the sense of say an "encyclopedia of mathematics" (for example along the lines of the Encyclopedic Dictionary of Mathematics published by MIT press). We are really addressing a very wide audience to whom the entry should provide some useful information. I agree that rigorous and extremely general definitions (such as functions on Banach manifolds) have to be somewhere in Wikipedia

The present state of the article is a bit like having an article on group theory that only discusses permutation groups, or an article on manifolds that only discusses submanifolds of Rⁿ, simply because it's easier, more elementary, and closer to the order that things happened historically.

I think this is a bad comparison, because someone that happens on differentiable manifold will likely have more sophistication than somebody that stumbles on derivative.

--CSTAR 22:48, 26 Jun 2005 (UTC)

Someone who happens on the derivative will likely have more sophistication than someone who's learning addition. Should every article be dumbed down to the lowest level of possible reader? I think differential manifold should start out with a correct and complete defintion, and then contain a subsection about the "intuitive meaning". Similarly, I think derivative should start out with a complete and correct description, and then have an intuitive description. My 2¢. -Lethe | Talk 04:23, Jun 27, 2005 (UTC)

I agree with CSTAR. Also, I think way too often mathematicians fall into temptation of writing articles only they understand.

And about the paralel with manifold. There is lot of discussion on its talk page now, because the current version of article seems to be written by differential geometers for differential geometers. That's not good on a general purpose encyclopedia. Oleg Alexandrov 00:00, 27 Jun 2005 (UTC)

Fair enough, I agree that manifolds are a poor example. Let me try another one, which I hope will illustrate my point more effectively. Consider the article continuous function. This is certainly something that a first year college student might look up (possibly even a high school student). I think continuous function does a much better job of handling different audiences than the current version of derivative (although incidentally in my opinion it still needs a lot of work... some pictures would be nice). It starts out with a fairly wishy-washy description in terms of input values having effects on output values, without saying too much about what kind of functions are being discussed. Then it gives some specific examples, which happen to be real-valued functions of real numbers. Then it has a paragraph discussing generalisations, which link immediately to Continuity (topology) which gives the most general definitions of continuity in mathematical use. The next section of the article is called "Real-valued continuous functions" and is very explicit about its restricted scope. I think that the Continuous function article manages all of this without in any way "scaring off" a first-year undergrad; if anything it might just pique their curiosity.

In contrast, the introduction to Derivative gives not the slightest indication that the concept leads to something far more general. There's a really nice sentence later in Derivative, The common thread is that the derivative at a point serves as a linear approximation of the function at that point. I think it would be great if something like that could appear in the intro. I'm not going to write it now because there seems to be a lot of opposition, but if I get any support here (HINT HINT), maybe I'll try. Dmharvey File:User dmharvey sig.png Talk 00:19, 27 Jun 2005 (UTC)

I'd like to see something more like what you're describing. -Lethe | Talk 04:25, Jun 27, 2005 (UTC)

Sounds like we're all in violent agreement, then. Its easy to have a vision of how things should be; its much harder to make it so. User:Dmharvey seems to be a very capable editor; if he wants to do this work, I say carte blanche. linas 04:43, 27 Jun 2005 (UTC)

Dmharvey: One word of caution: there are appearently not-infrequent proposals and attempts to "improve" major math articles, which more often than not end in shame and failure (and which the "rest of us" have to then clean up after). So there is certainly nervousness. Use caution. linas 04:58, 27 Jun 2005 (UTC)

I admit the error of my ways

Well, not quite. But the article, I realize, doesn't say anywhere what the derivative is in what I would regard as a mathematically correct way. That's bad. Nevertheless, the intro (pre TOC) grafs are OK (although possibly redundant). --CSTAR 28 June 2005 03:57 (UTC)

An attempt to rewrite the introduction

I will follow linas's advice. Caution is called for. Therefore, I put up for discussion/amendment the following rewrite of the introduction to Derivative.

In mathematics, the derivative is one of the two central concepts of calculus. (The other is the integral.)

The simplest type of derivative is the derivative of a real-valued function of a single real variable. This is the kind of derivative usually encountered in a first course on calculus, and historically was the first to be discovered. It measures the rate at which the function's value changes as the function's argument changes. That is, it provides a mathematical formulation of the notion of rate of change. Moreover, the derivative is an extremely versatile concept that can be viewed in many different ways. For example, the derivative can be used to determine the slope of a tangent to the graph of the function. Under this geometrical interpretation, derivatives can be used to determine many geometrical properties of graphs of functions, such as concavity or convexity.

There are also many generalizations of the derivative. The common thread to these generalizations is that the derivative of a function at a point should serve as a linear approximation of the function at that point. Perhaps the most natural situation is that of functions between differentiable manifolds; the derivative at a certain point then becomes a linear transformation between the corresponding tangent spaces.

The remainder of this article discusses only the simplest case (real-valued functions of real numbers).

The new article Derivative (generalizations) will basically contain the list that is currently under the section heading Derivative#See also. Incidentally, I think it would be appropriate for many of the entries in that list to have a one sentence summary.

Some comments I would like to make before the free-for-all begins.

• Although some of the old intro made it to my rewrite, I have trimmed some of it in the interests of balancing introduction length against new material. People may not agree with my choices. Please make yourself known.
• In particular, I was a little sad to lose

It should be noted that not all functions have derivatives. For example, functions do not have derivatives at points where they have either a vertical tangent or a discontinuity. However, functions may fail to have derivatives even if they are continuous and have no vertical tangents.

However, I don't think this belongs in the new-fangled introduction. There is already a short discussion of non-differentiability later in the text.

• I have changed "anti-derivative" to "integral". (I would want to make this change regardless of any rewrite of the intro.) The anti-derivative is a tool used to compute integrals; this is justified by a theorem (the fund. theorem of calculus in its various guises). To put it another way, one does not introduce the two branches of calculus, differentation and anti-differentation. One instead introduces differentation and integration, each of which can be described naturally and independently from the other; then proves the remarkable fact that they are inverse operations, and hence that anti-derivatives can be used to compute integrals.
• I guess some minor changes would need to be made to the Derivative#Generalizations section.

Dmharvey File:User dmharvey sig.png Talk 28 June 2005 12:03 (UTC)

It is better than what we have currently. Unfortunately it doesn't say anything about (in the intuitive meaning) smoothness and continuity. Nor about the slope of a graph. These things are visual intuitive aids.--MarSch 28 June 2005 12:57 (UTC)

Actually it does mention the slope of the graph. Precisely one sentence. Take another look. Dmharvey File:User dmharvey sig.png Talk 28 June 2005 14:16 (UTC)

You are correct, but it should be one of the first things to say, not the last before going on to generalizations. --MarSch 29 June 2005 13:31 (UTC)

Another attempt at the intro

OK, how about this:

In mathematics, the derivative is one of the two central concepts of calculus. (The other is the integral.)

The simplest type of derivative is the derivative of a real-valued function of a single real variable. It has several interpretations:

• The derivative gives the slope of a tangent to the graph of the function at a point. In this way, derivatives can be used to determine many geometrical properties of the graph, such as concavity or convexity.
• The derivative provides a mathematical formulation of rate of change; it measures the rate at which the function's value changes as the function's argument changes.

This derivative is the kind usually encountered in a first course on calculus, and historically was the first to be discovered. However, there are also many generalizations of the derivative. The common thread to these generalizations is that the derivative of a function at a point should serve as a linear approximation of the function at that point. Perhaps the most natural situation is that of functions between differentiable manifolds; the derivative at a certain point then becomes a linear transformation between the corresponding tangent spaces.

The remainder of this article discusses only the simplest case (real-valued functions of real numbers).

Dmharvey File:User dmharvey sig.png Talk 29 June 2005 15:30 (UTC)

Good, but I think the relation between the derivative and the integral should be stated directly. Fredrik | talk 29 June 2005 15:50 (UTC)

What if we replace

In mathematics, the derivative is one of the two central concepts of calculus. (The other is the integral.)

with

In mathematics, the derivative is one of the two central concepts of calculus. (The other is the integral; the two are related via the fundamental theorem of calculus.)

??? Dmharvey File:User dmharvey sig.png Talk 29 June 2005 15:58 (UTC)

I don't like the wording, but I can't think of anything better either. It can be edited later, of course. - Fredrik | talk 29 June 2005 16:21 (UTC)

By the way, may I ask a WP etiquette question? On the one hand I've been told it's bad form to edit a discussion page. On the other hand, for a discussion like the one taking place here, it would be much more pleasant to simply edit the proposed introduction in-place. What's the best thing to do here? Thanks. Dmharvey File:User dmharvey sig.png Talk 29 June 2005 15:58 (UTC)

Be bold! But don't be suprized if your edits get edited later. :) Oleg Alexandrov 29 June 2005 16:18 (UTC)

OK, well I'm just going to try it and see what happens.... Dmharvey File:User dmharvey sig.png Talk 30 June 2005 15:43 (UTC)

move to differentiable function

Since this article is basically only about differentiable functions and not about the much more general concept of a derivative, perhaps it would be a good idea to move to differentiable function, which currently redirects here. It would also be the right place for my recently created stub differentiabillity class. Smooth function might be merged also. --MarSch 30 June 2005 13:20 (UTC)

Hmmmm. I agree that the present version is not about "the derivative" in general, but I don't think it's that much closer to "differentiable function". (After all, differentiable functions include many more than just the real function of a real variable case presently covered here.) With its present content, the article should really be called Derivative (high school version) (or a more tactful version thereof). My proposed replacement introduction at least gets it a little closer to what should go in Derivative. I would be interested to see what kind of material you would propose putting in a more general Derivative article, if we moved the present title to something like Derivative (high school version). I would think the huge variety of concepts of derivative would make it rather difficult to do this in a coherent way; all I can really think of putting there is a list of all the generalizations of the high-school version. Dmharvey File:User dmharvey sig.png Talk 30 June 2005 15:38 (UTC)

I disagree with any move. Wikipedia is not an encyclopedia for mathematicians, rather for the general public. As such, it is more appropriate that the concent of derivative as taught in calculus is the article featured at derivative, and any extensions or generalizations be featured in a more specialized article. Oleg Alexandrov 1 July 2005 02:16 (UTC)

Why can't wikipedia be an encyclopedia for mathematicians too? That's certainly something I see wikipedia as having the potential for. Why else would we have an article about, say, the K3 surface? Certainly that's not here for the general public. Anyway, I also disagree with the move. Why on earth would we want something other than the derivative to be in an article named derivative? -Lethe | Talk July 1, 2005 17:41 (UTC)

I agree: through the magic of hyperlinks and well-written prose, WP can be an encyclopaedia for both mathematicians and normal people (i.e. non-mathematicians). In any case, the article should be about the derivative (either high-school or advanced version), not about differentiable functions. Dmharvey File:User dmharvey sig.png Talk 2 July 2005 12:52 (UTC)

I agree that this encyclopedia can be for mathematicians too, it is just that it is not primarily for them. When deciding what should be in an article, one should make sure not to err towards making the article more for mathematicians than for everybody else. Oleg Alexandrov 2 July 2005 15:43 (UTC)

Actually I was a bit surprised that differentiable function doesn't exist and since it redirected here... I think it is better if smooth function and differentiability class are merged to diff function. --MarSch 2 July 2005 15:30 (UTC)

Don't say derivative (high school version); say derivative (elementary calculus), or something like that. Michael Hardy 5 July 2005 01:03 (UTC)

That sounds much better. I'd love it if the current Derivative (generalizations) got moved to Derivative and the current Derivative got bumped to Derivative (elementary calculus), with the appropriate modifications to the introductions. I realise that's controversial, and the underlying question is: what do we want our various audiences to see when they search for "derivative". My rationale is that the article under the word "Derivative" should be about the full scope of the concept, regardless of the fact that most people, when searching for "derivative" would "expect" to see only the elementary calculus version. An example of a structure I regard as fairly good is the relationship between current versions of Algebra and Elementary algebra. There's probably a lot of hits to Algebra from high school kids, and I'd hope they'd find Elementary algebra quickly. (If they don't, something's wrong with the page.) Dmharvey File:User dmharvey sig.png Talk 5 July 2005 11:21 (UTC)

I'd probably agree with this move once derivative (generalizations) were in a more complete state, including a nice meaty three paragraph section on the elementary single variable derivative. -Lethe | Talk July 5, 2005 15:46 (UTC)

The algebra thing is more complicated, as there you have elementary algebra, algebra, and abstract algebra. Either way, since the derivative is a very important article, I would oppose moving it without a lot of discussion and quite a bit of votes for the move. Oleg Alexandrov 5 July 2005 15:49 (UTC)

Agree discussion is required. There's certainly no rush. We should probably leave it aside for the moment and revisit when Derivative (generalizations) is more complete. Dmharvey File:User dmharvey sig.png Talk 5 July 2005 16:20 (UTC)

I think that it is good the way it is. Derivative is a much more common term and this article deals with said topic. At the same time differentiable function implies the article talks more about what a differentiable function is and most of those who come to wikipedia will know it as the derivative anyway and in this instance if the majority of the inquiries are for derivative, that is what the main article should be.Guardian of Light 5 July 2005 19:05 (UTC)

antiderivative or integral

I disagree with the notion that the two central topics in calculus are the derivative and the antiderivative (these are probably two different ways of looking at the same topic). The two topics are the derivative and the integral. The integral and the antiderivative, while closely related by the fundamental theorem, are conceptually quite distinct. -Lethe | Talk June 30, 2005 14:10 (UTC)

My proposed new introduction addresses this issue. (See above). Dmharvey File:User dmharvey sig.png Talk 30 June 2005 15:29 (UTC)

Oh I see you actually did it :-) Dmharvey File:User dmharvey sig.png Talk 30 June 2005 15:40 (UTC)

Differentiation and differentiability

This section duplicates the following sections and is not very well written. Maybe the last few lines contain new information, but most of it can be eliminated. --MarSch 30 June 2005 16:54 (UTC)

It certainly looks more like a list of possible notations than a discussion of differentiation and differentiability. Though I notice that not all the different notations are listed in the section on notations. -Lethe | Talk June 30, 2005 16:58 (UTC)

Yes, the alternate notations need to be conserved, but the pronounciations are bogus. --MarSch 30 June 2005 17:56 (UTC)

I agree with MarSch that the pronounciations don't deserve the attention they were given in the article. How about cutting them off altogether? Oleg Alexandrov 1 July 2005 02:11 (UTC)

I've cut the pronounciations:

This definition is discussed in more detail below. If f is a function, the derivative of the function f at the value x is written in several ways:

$f'(x)\quad$

pronounced "f prime of x" or "f dash of x"

${\frac {d}{dx}}f(x)$

pronounced "d by d x of f of x" or "d d x of f of x".

${\frac {df}{dx}}$

pronounced "d f by d x" or "d f d x"

$D_{x}f\quad$

pronounced "d sub x of f"

${\dot {x}}$

pronounced "x dot", indicating dx/dt.

Recent changes to this article

I find the new rewrite of the introduction rather incomprihenseble to non-mathematicians. What do people think? Oleg Alexandrov 04:13, 1 August 2005 (UTC)

Fully agree with Oleg. I was about to say something similar myself. I would support a wind-back, although there are perhaps a handful of minor improvements that the current version has. Dmharvey File:User dmharvey sig.png Talk 10:54, 1 August 2005 (UTC)

I am not going to do anything about this article, as I already reverted this contributor's changes at integral and neighbourhood (mathematics). So I would like to make it clear that I have nothing personal against the contributor VKokielov, it is just the math articles are the way they are (meaning elementary and without much mathematical depth in the introduction) for a purpose, to make it easier for non-mathematicians who visit Wikipedia. Oleg Alexandrov 15:41, 1 August 2005 (UTC)

Better than a wind-back would be to move it down to Generalizations (and a new section called Rigor, a condensed version of Spivak's Calculus?), where much of it belongs. But there should be a rule of thumb: WP articles ought to be written for people who don't already know the subject of the article. Septentrionalis 21:49, 1 August 2005 (UTC)

If you had something personal against me, you wouldn't be the first - and so it wouldn't stand in the way of anything.  ;) Besides, around these topics, to be called incomprehensible is (how strange that is!) a compliment. --VKokielov 04:18, 3 August 2005 (UTC)

It depends on whom it is that says it is incomprehensible, Oleg is a mathematician whose opinion is worth listening to. I liked the earlier version myself. --CSTAR 14:46, 3 August 2005 (UTC)

Re:to be called incomprehensible is (how strange that is!) a compliment.

Wow. then I'm loaded with compliments! You should see all the "compliments" I get from Bell's theorem and Many-worlds interpretation. --CSTAR 15:40, 6 August 2005 (UTC)

Why is the introduction now two pages long? Surely this is getting out of hand. Dmharvey File:User dmharvey sig.png Talk 10:42, 6 August 2005 (UTC)

I think the introduction to derivative before VKokielov's changes was just right, and now it is indeed getting out of hand. In the same time, the derivative (generalizations) badly needs a higher level introduction. VKokielov, what if we move your introduction to the latter article, where you can afford to be more mathematical? Oleg Alexandrov 15:04, 6 August 2005 (UTC)

The intro has the statement about the third paragraph down

The derivative of a function at a local value x₀.

What is a local value? --CSTAR 15:37, 6 August 2005 (UTC)

I reverted back to the old (27 of July) introduction (somebody had to do it). I suggest that energy better be spent improving the derivative (generalizations) article, rather than fixing this one which is not broken. Pmanderson, I am sorry to have also removed some of your fixes, your intent was good, but the introduction was rather broken recently, and I think a revert was a better way to take care of it. Oleg Alexandrov 16:57, 10 August 2005 (UTC)

That's fine; but this paragraph should be merged back in lower down:

The derivative is a local limit, "derived" (hence the name) from functions subject to certain local conditions. That the derivative is a local limit means that, for any point where the function is defined (and fulfills the local conditions), the derivative is a number or set of numbers. In short, the derivative itself is a function; so derivatives (or thus "derivative" functions) are subject to functional analysis. The function from which a derivative is derived is called the antiderivative of that derivative (sometimes, by analogy to integrals, the indefinite integral; but in the current terminology this symmetry of names is meaningful only in the special case of functions of one independent variable).Septentrionalis 17:05, 10 August 2005 (UTC)

Please feel free to merge it if you feel it is useful. I found it terribly complicated. Let us see what others say. Oleg Alexandrov 17:26, 10 August 2005 (UTC)

After Oleg's reversion

I support Oleg's revert action. Dmharvey File:User dmharvey sig.png Talk 16:55, 10 August 2005 (UTC)

I second the support of Oleg. I know how important it is in Wikipedia to fell validated :) --CSTAR 17:04, 10 August 2005 (UTC)

Definition of "x-dot"

In the first instance of ${\dot {x}}\;$, where all the different ways of expressing f(x) are discussed, shouldn't it be ${\dot {f}}\;$ instead? Note that further down in the article, the function ${\frac {dx}{dt}}\;$ is expressed as ${\dot {x}}\;$ instead of ${\dot {t}}\;$. (Not an expert here, forgive me if I'm wrong!) Agent Zero 19:34, 9 August 2005 (UTC)

you are correct --MarSch 18:03, 25 September 2005 (UTC)

Help with a problem

For my GCSE maths homework, I have been told to research differentiation and, naturally, I came here but I can't make head nor tail of it. I will give you some background. We have just started some coursework about maximizing the volumes of trays. Here is the statement,

When the area of the sdides of the tray are at the same as the area of the base, the volume is at a maximum.

I have found out, using algebra and examples, that this is true but our teacher said that to get top marks, we need to learn about differenciation and throw that in somewhere. She won't tell us what it is or how to use it: we have to work it out. I am not asking you to do my homework for me but at least give me a start, or change the article so that it is easier for a lay reader (like myself) to understand. Could someone please help me? --Celestianpower ^hab 17:33, 20 September 2005 (UTC)

Changing the article won't help. You need to know how to apply the derivative, and not as much how it is defined. I know a classical problem which is close to what you have in there. That one says that one has a square piece of cardboard, which one makes into an open box after cutting off some corners and gluing the thing together. If one denotes the base of the obtained box by x, one will probably get a volume function of the form

$V(x)=x\cdot x(1-2x)$

or so. Now, if you want the volume to be maximal, which means you will be at a stationary point, that is, the derivative of V is zero. Differentiate the above, set it equal to zero, and solve for x. That will give the answer.

Your problem might be different, but that's the basic idea. First find the volume function, take its dervivative, set what you get to zero, and solve the equation. Give it a try and see if it works. Oleg Alexandrov 00:03, 21 September 2005 (UTC)

Hmm. I stil don't understand, sorry. That is the same problem more or less but how do you find the derivative and set it to zero? The formula for the maximal volume of any box (where x is the length of one of the sides) is

2x³ / 27

I'm sorry for being a pain but can you help me? --Celestianpower ^hab 14:50, 21 September 2005 (UTC)

I don't think this is the right formula for the volume. This allows the box to be as big as it wants and same for the volume, which would imply inifinite box with infinite volume. There must be some constraints which keep the box from increazing too much.

Now, to find the derivative, you need to use the power rule, which says that the derivative of x^3 is 3x^2, which multiplied by 2/27 will give the answer (x^2)*6/27, which can be simplified. After you set it equal to zero, you would get x=0, which is the wrong answer, because I think your original volume function is not right. Oleg Alexandrov 15:25, 21 September 2005 (UTC)

I assure you that it is. The largest volume that can be made from a piece of card 18cm by 18cm is

(2 * 18³) / 27

which equals 432, the same figure as what I get if I do it on a spreadsheet or by hand. Does that help? --Celestianpower ^hab 17:15, 21 September 2005 (UTC)

OK, I misunderstood you. You need to explain how you make a box from a piece of cardboard. Do you make square cuts at the corners of the cardboard? Do you have an open box or a closed box? You see, you can't just fold a piece of cardboard in a box without overlaps or without cuts. And whether the box is open or not will change the answer. Oleg Alexandrov 17:30, 21 September 2005 (UTC)

No - I should have made myself clearer. If you have an 18cm by 18 cm square of card and cut out the corners so that the area of the base is equal to the area of the 4 sides and glue into an open tray, the volume can be worked out by the above formula (using x as the length of the sides of the original sides of the card). Does that clear things up? --Celestianpower ^hab 17:40, 21 September 2005 (UTC)

So, originally, the side of the card is 18 cm. At the beginning, you don't know the size of the square corners you cut, so you denote them by x (this is now a true unknown, unlike your x above). Once you chop from a segment of length 18 the length x twice (once for each end) you are left with a side of 18-2*x. When you fold the thing, the box gets a height, which is x. So, you obtain an open box of base 18-2x by 18-2x and height x. Please do not read the next paragraph until you make a drawing and convince yourself that what I say makes sense. And keep in mind, we don't know yet what x is.

Now, after folding the thing, a box with base 18-2x by 18-2x and height x has volume (width times breadth times height) of

$V(x)=(18-2x)(18-2x)x.$

Multiply this through. Take its derivative (use the sum rule and the power rule, see the derivative article). Set the derivative to equal zero. Solve for x. You will get two answers, hopefully only one of them will be positive. That will be the correct x, which if you plug back in V(x) should give you the volume you want. Oleg Alexandrov 18:14, 21 September 2005 (UTC)

I really, really don't want to sound ungrateful but I already know the majority of what you said - and have done it extensively (its what I meant when I said "I have found out using algebra". What I asked is how to use the sum and power rules to take its derivative. The article doesn't make any sense to me. I'm really sorry if this sounds ungrateful because it isn't supposed to. And I'm making myself so unclear and looking like a right ninny at the same time. --Celestianpower ^hab 20:13, 21 September 2005 (UTC)

OK.

$V(x)=(18-2x)(18-2x)x\,$

$=18^{2}x-4x^{3}.\,$

$V'(x)=\left(18^{2}x-4x^{3}\right)'\,$

$=\left(18^{2}x\right)'-\left(4x^{3}\right)'\,$ (sum rule)

$=18^{2}\left(x\right)'-4\left(x^{3}\right)'\,$ (constant rule)

$=18^{2}\cdot 1-4\cdot 3x^{2}\,$ (power rule)

$=18^{2}-12x^{2}.\,$

You need to set this equal to zero and solve for x. This assuming that I did the calculation right. Oleg Alexandrov 20:36, 21 September 2005 (UTC)

Hey, Celestianpower, I get no thanks? :) Sorry it took me so long to understand what you want, but did this help? Oleg Alexandrov 22:53, 25 September 2005 (UTC)

Yes - of course you do! Thank you very much. I asked a second opinion and have now cracked it in my own head. It's easier actually conversing with a person I find. Here it is:

When x is the length of the paper originally, and y is the length of cut off, the formula is such:

$V=y(x-2y)(x-2y)$

This turns into:

$V=yx^{2}-4xy^{2}+4y^{3}$

We differentiate for y:

dv/dx = x^2 - 8xy + 12y^2</math>

When dv/dx = 0, the equation reads thus:

$0=x^{2}-8xy+12y^{2}$

Then we factorise:

$0=(x-2y)(x-6y)$

Therefore y equals either

$x/6$

or

$x/2$.

This is what I wanted and if verifies my other work. Again, thank you. Perhaps I'll get a good coursework mark now... --Celestianpower ^hablamé 16:09, 26 September 2005 (UTC)

operator notation

Where would be the correct place to discuss

$(L_{a}f)(x):=f(x+a)$

$f':=\lim _{a\to 0}{\frac {L_{a}f-f}{a}}$?

this notation could also make the proof of the product rule more readable.

--MarSch 13:10, 28 October 2005 (UTC).

I have no idea where to put that. The section on notation in this article is already too big, with three subsections, etc. I would suggest trimming it a bit. Oleg Alexandrov (talk) 13:33, 28 October 2005 (UTC)

Merge

Shouldn't the article Derivation (abstract algebra) be merged into this article? Jon Harald Søby \ ^{no na} 07:07, 4 November 2005 (UTC)

No, I think at great length, it's been decided to keep this article just for the simple derivative of a real function in one variable. See the scope section above. -Lethe | Talk 10:34, 4 November 2005 (UTC)

Agree with Lethe. Maybe something about derivation (abstract algebra) be said in derivative (generalizations) instead. Oleg Alexandrov (talk) 16:41, 4 November 2005 (UTC)

It's already there, in the Algebra section. Dmharvey File:User dmharvey sig.png Talk 01:04, 5 November 2005 (UTC)

Thanks, I should have checked first. Oleg Alexandrov (talk) 01:45, 5 November 2005 (UTC)

People more knowledgable on the topic may want to merge any relevant or intersting information from the old version of the Differential calculus page [1] which now redirects here. It was terribly formatted but there may be something in it. Cormaggio ^@ 18:58, 22 November 2005 (UTC)

mulitplying derivatives

I'm very skeptical about when people multiply both side of an equation by dx, for example if dy/dx=x^2, they multiply both sides and get dy=x^2dx. In the article it clearly says you cant cancel out or multiply dx, but everywhere I look they seem to do so. I am confused, can someone explain? --anon

Indeed, you cannot cancel out or multiply by dx. That becuase dx is not a number, it is just a symbol, and dy/dx is not a fraction, just looks like one.

However, when solving differential equations, more precisely when doing separation of variables it is very useful to pretend you actually can treat dx and dy as purely numbers. This always gives right results (that's why people use it :) but this trick is not necessary.

I did not answer your question completely (hopefully other people will fill in) but that's the basic idea. Oleg Alexandrov (talk) 05:28, 2 January 2006 (UTC)

Thanks for your reply, I figured out one of my problems with multiplying differentials, and that concerns the substitution rule. But with differentials equations, what does it mean if we have for example dy-xdx=0? All I can make of this is that an infinitesimal change in y minus x times and infinitesimal change in x. However, the concept of derivatives and integrals is all defined upon limits, and that implies one cannot speak of infinitesimal number with mathematical rigor. Does it just define a relation, and has no real meaning on its own? --anon

Indeed, I don't think it has much meaning on its own. Is a formal ("symbolic") if you wish way of writing things. One encounters those things in differential forms, but even there it has no real concrete meaning, in the same way that for example as having an expression of the form $X^{3}-5Xy+7Z$ where X, Y and Z are some indeterminate symbols. Oleg Alexandrov (talk) 03:16, 4 January 2006 (UTC)

Thanks you've being a lot of help :)

are boundary points critical points?

The article states that critical points are where the derivative is undefined or zero, and that local extrema only occur at critical points. But clearly functions on the unit interval can have local extrema at their endpoints, and the derivatives can be nonzero and defined there, using one-sided limits. The statement as it stands is therefore wrong, but I'm unsure as to whether the correct remedy is to allow boundary points of the domain to be critical points, or to change the result to say that extrema occur at critical points or boundary points. -lethe ^talk 23:54, 3 January 2006 (UTC)

Personally, I'd go for the latter definition. It looks like the section we currently have only considers functions on the entire real line. —Ilmari Karonen (talk) 23:11, 4 January 2006 (UTC)

Macroscopic change

The phrase "macroscopic change" links to this page. I was wondering why that is, since that phrase is never discussed on this page. I found the link to macroscopic change on the page for "delta". A derivative is an infintesimal change, which seems to me would also be the meaning of "microscopic change", which links to the page "differential". Does anyone know if a differential is the same thing as a derivative? or what the difference is? Also, what is a macroscopic change? is it an average change? Fresheneesz 22:11, 10 February 2006 (UTC)

Denoting the derivative at a point

"We can write the derivative of f at the point a in two different ways:

${\frac {d\left(f(x)\right)}{dx}}\left.{\!\!{\frac {}{}}}\right|_{x=a}=\left({\frac {d\left(f(x)\right)}{dx}}\right)(a).$"

I've never seen the second notation ever before ever (probably because it looks like you're multiplying by a... horrible notation). Sorry if that is redundant, but i've *always* *always* *always* seen the notation $f'(a)\!\$ or ${\frac {df(a)}{dx}}\!\$ to denote the derivative at the point a. Should I add this? Fresheneesz 01:12, 11 February 2006 (UTC)

Recent edits to this article

I disagree with the recent edits to this article by Fresheneesz. First, the variables should be italic, and one should write ==Introduction== and not ==Intro==. More importantly, the "real" defintion was not on top for a purpose. It is good to start things with motivation, with the heavy things later (like limits). Comments? Oleg Alexandrov (talk) 01:55, 11 February 2006 (UTC)

Besides, the notation is inconsistent, with the point at which the derivative is taken denoted both $x$ and $x_{1}$, which would be confusing. Oleg Alexandrov (talk) 01:57, 11 February 2006 (UTC)

Ok, I do see how the notation would be confusing. The definition could define what x1 and x2 are vs just x. Personally I think the best way to explain things is to give the full definition first, then explain where it comes from bottom up (so.. top, then bottom up). This way people learning about it can have full perspective while they do so, instead of blindly learning triva after trvia until finnally at the end the truth comes out. Its also very nice to have the full definition at the top, because then its easy to find for people looking for a simple reference. Most likely, many people come to this page because they've already learned something about it, and don't really need the entire article. I'll fix some of the inconsitancies though. Fresheneesz 02:38, 11 February 2006 (UTC)

I touched it up with italics. I was also going to add this pharagraph, but I thought i might as well put it here first before putting it on the page:

Conceptually, the derivative is a rate of change of a function, which can be visulized by the slope of the graph of the function at a certain point. An analogy is that the derivative is like a velocity - one can change their speed, but at a given time, one has an "instantaneous" velocity (derivative). Just like velocity, a function's slope can change, but at any given point on the graph, the graph has an "instantaneous" slope - a tangent line.

-Fresheneesz 04:31, 11 February 2006 (UTC)

I removed the big formula at the top. I suggest you read carefully the whole article, not just here and there as you like to do, and see that the article was carefully written in such a way as to arrive at the formula at the appropriate time.

I would be strongly opposed if you start modifying articles by putting the complicated parts on top, at least not until you have been here for a while, got familiar with the existing Wikipedia style, and encountered more of the less mathematically inclined readers and editors. Also please take my advice about reading Wikipedia:Make technical articles accessible.

About the new paragraph you would like to add, that would be nice. But please bear in mind that that information is already in various places in the article, with the slope mentioned in the intro, and the velocity in the section about physical interpretation.

I would suggest you read very carefully the entire article before making big changes. Quite a bit of people worked on it, and it would be nice if things fit together. Oleg Alexandrov (talk) 17:30, 11 February 2006 (UTC)

Ok, I read the link you suggested. I'll agree with your changes, and now there is at least a concrete definition at the top. Sorry if I'm being too bold. I noticed, though, that you changed the header "Algebraic manipulation etc" back. Perhaps "finding the derivative" is an inaccurate addition to that header, but I was going for a more meaningful name - since "algebraic manipulation" doesn't pop out to me as rules for differentiation. Perhaps we could rename that header just "Rules for Differentiation" ? Like it says in Wikipedia:Make technical articles accessible, a good table of contents helps an article be searchable. Fresheneesz 20:56, 11 February 2006 (UTC)

I was kind of terse above, sorry. You are right about the heading, what I did not like was that the way you made it it was too long, and I could not know how to shorten it. Now I renamed it to "Rules for finding the derivative". If you like "Rules for differentiation", you could as well rename it again. Oleg Alexandrov (talk) 00:20, 12 February 2006 (UTC)

It looks fine. The only thing I can think of adding to this page is to explicitly state that the definition of the derivative (the limit) *is* the limit of a change in the function output as the change of x goes to 0 (Δy/Δx). When I first learned about derivatives, I always thought it was just another magical formula. But noting what its really saying might help people better understand it. Fresheneesz 00:44, 13 February 2006 (UTC)

I think the way the intro starts is with the "instantaneous rate of change". Is that what you want? Oleg Alexandrov (talk) 01:01, 13 February 2006 (UTC)

Spatial Derivative

The page heat equation links to this page when talking about a "spatial derivative". there is no article on spatial derivative, and I think some mention of whatever a "spatial derivative" is would be nice to User: fresheneesz

The heat equation is $u_{t}=u_{xx}$. The t variable is called the time variable, and the x variable is the spatial variable. So there is nothing special about it. If anything, it needs to be clarified in the heat equation article. Oleg Alexandrov (talk) 01:34, 16 February 2006 (UTC)

Finding inflection points where f''(x) equals zero

All in all the derivative article is a very solid piece of work, but it baffles me that it's not mentioned with a single sentence how important this field of mathematics has become in financial analysis/prediction as well as statistical analysis/prediction. Yes, physics is the most useful field. But it still baffles me I must admit.

Inflection points of a graph can, and is often used, to predict a change in growth of a phenomena. Be it CO2 emission, world population, average temperature change, stocks on exchanges, and much more.

Also, I feel that this article does not show to the reader clearly enough how derivative is used for graph analysis in general.

(I refer to http://www.clas.ucsb.edu/staff/lee/Inflection%20Points.htm for reference)

The--dud 12:48, 25 February 2006 (UTC)

---

Whereas the concept of derivative(s) are ineherent, germane, and critical to the role of economics, a concern in which we all participate, I move to add the following post discussion and modification:

Economics - The functional basis of fiat-based banking.

Symmetric difference

My revert was not quite well explained. Of course using symmetric difference will make for a higher order accuracy, so O(h^2) instead of O(h). However, you cannot use the symmetric difference as a definition, as then the absolute value would be differentiable at zero, and it is not.

Anyways, I found that addition not so helpful, and removed it. Oleg Alexandrov (talk) 18:59, 19 May 2006 (UTC)

---

Hi!

This is me who added symmetric derivative thing.

Actually I wasn't talking about definitions, but about correct calculating of derivative [you were right in your comment when mentioned that it's applicable for numeric stuff]. I didn't find anything about it on wiki, so I think it should be added something like that:

If:

1. There exists left-derivative;

2. There exists right-derivative;

3. They are equal,

than derivative can be calculated more precisely with following formula: $\lim _{h\rightarrow 0}{\frac {f(x+h)-f(x-h)}{2h}}$.

How about that?

I really don't think that information belongs right in the section where the derivative is defined. It is distracting and too offtopic, I think. That information should be better off somwhere at finite difference, I'd think. Oleg Alexandrov (talk) 22:37, 19 May 2006 (UTC)

I agree that it should not be said here. But also I think you should correct this article [because your corrections will be more correct, I believe]: Numerical differentiation

It's said there that $h$ can be positive and negative;

nobody is talking about existance of derivative in the point (equality of left and right derivatives);

and no any example of curves that can not be calculated this way (absolute value). I think all these remarks are important! Thank you!

I am not sure how important is to discuss in that numerical differentiation article whether derivatives exist. That one is a numerical articles, so you assume things are as nice as necessary. In short, finite difference scheme belong in numerical articles, and existence of derivatives belong into articles like derivative. You are attempting to put in numerical derivatives in this derivative article, and theoretical isssues in the numerical article. I think it is better to keep things compartimetalized. More information is sometimes more confusing, not more illuminating, I would say. :) Oleg Alexandrov (talk) 00:29, 23 May 2006 (UTC)

Take a look at German version HERE

Pronunciation

The article gave the pronunciation as "dy by dx", expecting readers to know that "dy" would be pronounced as individual letters and "by" would be pronounced as a word. Does anybody read this stuff? Anyway, my request is that someone who knows how write it out phonetically. I think it might be something like /di waɪ baɪ di ɛks/, based on the IPA chart for English. --KSmrq^T 23:43, 19 May 2006 (UTC)

Techniques

I think that a few more things should be added could be added the on the rules of differentiation. For instance: ${\frac {d\log _{b}x}{dx}}={\frac {1}{x\ln b}}$ And other formulas for the differentiation of various kinds of functions. (Trigonometric, exponential, natural exponential, multi-dimensional, etc.) Or perhaps a new article should be created specifically listing such techniques.He Who Is 23:00, 3 June 2006 (UTC)

I think a new aricle would be nice to have. These techinques would take too much room in the already big derivative article. Anybody willing to make the techniques for differentiation turn blue? Oleg Alexandrov (talk) 00:40, 4 June 2006 (UTC)

I'll do it, but once I doubt I'll be able to add that much, so any additions thereafterare greatly appreciated. Also, I'm majorly obsessive compulsive. So I'm going to make it Techniques for Differentiation. He Who Is 01:36, 4 June 2006 (UTC)

Differentiation is not a proper noun, and Wikipedia naming conventions dictate lowercase, so please apply your OCD in compliance with guidelines, instead of in contravention of them. -lethe ^{talk +} 02:30, 4 June 2006 (UTC)

Yes, apply your ocd in compliance ... Oleg Alexandrov (talk) 03:29, 4 June 2006 (UTC)

I have to say that is a strange naming convention, considering that in the case of titles it is generally accepted that one capitilises the first word, as well as all following words aside from prepositions, linking verbs, articles, and a few others. Either way (If I remember correctly,) the first word of a title on Wikipedia is not case sensitive, so I'll just use Oleg's original link. He Who Is 16:06, 4 June 2006 (UTC) P.S. I also wish to note that I began to work on the article, then accidently exited the window and lost my progress. It being late (In my time, at least), I decided to simply get some sleep and do it in the morning, hence it will take slightly longer than expected. This time, though, I'll write in Word, so as not to loose it.

Objections

I think it might be insightful to include a few sentances about historical objections to the derivation of derivates. I remember reading somewhere some sort of clergyman-mathematician objected to the cancelation of terms that were going to be taken to zero in the x^2 example. This could be followed my a mention that the rigourous treatment provided by analysis solves quells any worries. 131.111.8.99 13:14, 8 June 2006 (UTC)

You're surely speaking of the Analyst by George Berkeley. -lethe ^{talk +} 13:24, 8 June 2006 (UTC)

I think 131.111.8.99's suggestion is a good one. I wanted to add a blurb about Berkeley's objections to calculus. But I am appalled to discover that this article has exactly no information about the history of the derivative, which is where such information would go. What gives? -lethe ^{talk +} 03:49, 9 June 2006 (UTC)

Small correction to Physics section?

A sentence states the following:

"For example, if an object's position on a line is given by"

which is followed by a non-linear function. Shouldn't the sentence read, "For example, if an object's position on a curve or parabola"? Or a linear equation could be used as the example? Excuse me if it's a dumb question, as I'm just a first-semester Physics major! --Dialecticas 17:43, 31 August 2006 (UTC)

About chain rule

Derivative of one variable with respect to another when both are functions of other variables: Let x = f(u,v) and y = g(u,v). Now dy / dx = ??.

if u & v are independent, then {(x,y)} is not a function. dy/dx is not defined. If u & v are interdependent, then dy/dx is defined. Jackzhp 23:01, 23 September 2006 (UTC)