Talk:Decagon

something wrong?

ive tried the construction method shown and everytime i seem to be way off. im just not getting 10 = points. —Preceding unsigned comment added by 71.232.147.54 (talk) 21:22, 4 April 2011 (UTC)[reply]

The construction is a bit tricky. Possibly you are not setting the correct radius at some point. Does the alternative method work OK for you? Dbfirs 09:29, 5 April 2011 (UTC)[reply]

the alt versions using the pentagons also seem to be a bit off. I know i can do it with a protracter, but there is a satisfaction to doing it with just a compass and straight edge, however I just can't seem to get any prescision. The final measure always seems to be off by a few degrees. my only guess is the measure must be very intolerant requiring perfect pin point measures with even the thickness of a pencil throwing me off or there is a flaw in determining the final radius wich determine the chord lengths. has anyone else actualy tried to draw these with pen and paper?

71.232.147.54 (talk) 18:24, 6 April 2011 (UTC)[reply]

I have gotten some very good and accurate results with Regular pentagon#Carlyle circles method that doesnt have the closer errors of the others seem to leave when i try to draft them. Bloodkith (talk)

Related figures

User:David Eppstein doesn't like these sections saying There appears to be NO SPECIFIC MENTION OF DECAGONS in Grünbaum's "metamorphoses", and as such this section is entirely without valid sources', so I moved them here. Tom Ruen (talk) 01:44, 5 February 2015 (UTC)[reply]

Hearing no objections, and references added, I'll move it back out. Tom Ruen (talk) 15:34, 12 February 2015 (UTC)[reply]

Well, back here again after another quick revert by User:David Eppstein: (Undo persistent reinsertion of badly-referenced (refs are to general concepts not its specific application) junk content (not relevant or useful to decagons) violating WP:NOTGALLERY).

How do you argue with someone who reverts content he doesn't like? Tom Ruen (talk) 17:35, 12 February 2015 (UTC)[reply]

The short answer: you build consensus of multiple authors that your version is appropriate, rather than just continuing to push that rock up the hill by yourself. WT:WPM is a good place to find mathematically-minded editors, if there are not enough who already have the page watchlisted. —David Eppstein (talk) 18:42, 12 February 2015 (UTC)[reply]

About this material: the parts on star polygons are present in all the higher polygon articles, as examples. Yes, the source speaks generally, but I fail to see why that should bar it from being used on the decagon – especially since this is a reasonably small polygon, so that {10/2}, {10/3}, and {10/4} are actually important polygons that arise very naturally in uniform polyhedra. The same goes for the isogonal variations. Perhaps decagram would be a better spot as that is specifically on star decagons.

As for the Petrie polygons: given the importance of Petrie polygons (and is there a relationship between the decagon's H₂ symmetry and these higher H₃ and H₄ polytopes?) I feel this should be included. I haven't checked that section of Regular Polytopes but especially given that these are low-dimensional polytopes that aren't part of infinite families (including even some Platonic solids!) that the decagon's role as their Petrie polygon would be specifically mentioned. So I've restored this part (but not those on the isogonal variations and star polygons, as those can go in decagram). Double sharp (talk) 13:20, 18 February 2015 (UTC)[reply]

David Eppstein reverted again to Double sharp restore, offering opinions of relative boredom and inaccuracy. Which reason should we argue against? Can we convince him he is not bored? Tom Ruen (talk) 19:24, 18 February 2015 (UTC)[reply]

User:David Eppstein: this is the most boring part of the "related" section. It's false that the Petrie polygons for 3d polyhedra are flat regular decagons and the higher ones are just general properties true for any polygon, not specific to decagons.)

Does the article state that it must be a flat decagon? No: the title is just "decagon", and the content is mainly about the "regular decagon". I think that with the appropriate caveat that these are skew regular decagons any issues regarding this could be averted. OK, I see that most of them are just one case in a series that goes on forever (the simplex, hypercube, orthoplex, and demihypercube), but I think for the lower ones especially (up to about 10D or so) this is interesting to give as an example. After all, we have articles on every regular polytope until 10D! Double sharp (talk) 03:04, 19 February 2015 (UTC)[reply]

Indeed, they are all regular skew polygons, and the best examples of them. You could limit the list to only the regular polytopes or those where all the vertices are on the petrie polygon (5-orthoplex, 9-simplex, and 5-5 duopyramid), but the others given are all the simplest regular and uniform polytope examples. I admit we could use a better explanation how skew regular polygons can be orthogonally projected into a planar regular polygon, but that fact is stated at the intro of Petrie polygon.

We know David Eppstein's reply now. He'll say "Unless Coxeter or someone with a professional reputation has published an explicit statement 'A 9-simplex has a 10-gonal petrie polygon which can be projected in the plane onto a regular decagon.', (and again on each polytope) this is OR, stating a special case of a general theory." Tom Ruen (talk) 03:53, 19 February 2015 (UTC)[reply]

Re-added the Petrie polygons (minus the harder-to-source 2H₂) here, while relegating the metamorphoses to decagram (this is the first example where star polygons can come into play, as t{5/3}={10/3} – which appears in many uniform star polyhedra, e.g. t{5/3,5} – so even if the higher ones are not kept this one probably ought to be). Double sharp (talk) 19:39, 15 March 2015 (UTC)[reply]

A regular decagram is a 10-sided polygram, represented by symbol {10/n}, containing the same vertices as the convex form. There is one regular star polygon: {10/3}, using the same vertices, but connecting every third points. There are also three which can be interpreted as regular compounds: {10/5} is reduced to 5 degenerate digons 5{2}, {10/4} is reduced to 2{5/2} as two pentagrams, {10/2} is reduced to 2{5} as two pentagons.^[1]^[2]^[3]^[4]^[5]

Form	Convex	Compound	Star polygon	Compounds
Image
Symbol	{10/1} = {10}	{10/2} = 2{5}	{10/3}	{10/4} = 2{5/2}	{10/5} = 5{2}

Deeper truncations of the regular dodecagon and dodecagrams can produce isogonal (vertex-transitive) intermediate star polygon forms with equal spaced vertices and two edge lengths.^[6] A truncated hexagon is a dodecagon, t{5}={10}. A quasi-truncated pentagram^[7], t'{5/2}, inverted as {5/3}, is a decagram, t{5/3}={10/3}. Other truncations form double coverings: t{5/4}={10/4}=2{5/2}, and t{5/2}={10/2}=2{5}.^[8]

Isogonal truncations of pentagon and pentagram
Quasiregular	Isogonal		Quasiregular Double covering
t{5} = {10}			t{5/4} = {10/4} = 2{5/2}
t{5/3} = {10/3}			t{5/2} = {10/2} = 2{5}

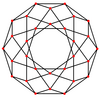
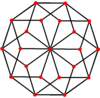
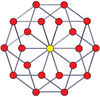
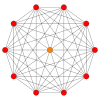
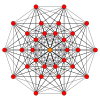
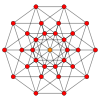
Petrie polygons

The regular decagon is the Petrie polygon for many higher-dimensional polytopes, shown in these skew orthogonal projections in various Coxeter planes:^[9] The number of sides in the Petrie polygon is equal to the coxeter number, h, for each symmetry family.

H₃				2H₂ (4D)
Dodecahedron	Icosahedron	Icosidodecahedron	Rhombic triacontahedron	5-5 duopyramid	5-5 duoprism
A₉	D₆		B₅
9-simplex	4₁₁	1₃₁	5-orthoplex	5-cube

References

^ Regular polytopes, p 93-95, regular star polygons, regular star compounds
^ Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38
^ Weisstein, Eric W. "Polygram". MathWorld.
^ Weisstein, Eric W. "Star polygon". MathWorld.
^ Weisstein, Eric W. "Star figure". MathWorld.
^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum, a {p/q} regular polygon can be transformed into {p/(p/2-q} by a continous sequence of intermediate isogonal polygons.
^ *Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 246 (916). The Royal Society: 411. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. {{cite journal}}: Invalid |ref=harv (help)
^ Coxeter, The Densities of the Regular polytopes I, p.43 If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consistents of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.
^ Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.

Jdhjf

Shape 102.132.217.64 (talk) 14:31, 30 August 2022 (UTC)[reply]

Side of the regular decagon

As depicted in the picture, the triangle $E_{10}E_{1}M$ has to equally long legs with length $R$ and a base with length $a$
The circle around $E_{1}$ with radius $a$ intersects $]M;E_{10}[$ in a point $P$ (not designated in the picture).
Then $E_{10}E_{1}P$ is a isosceles triangle with vertex $E_{1}$ and the length of a leg is now $a$ while the length of its base is $R-a\;$
The two triangles have equal angels (72°, 72° at the base and 36° at the vertex) and so they're similar, hence: $\;{\frac {a}{R}}={\frac {R-a}{a}}$
Multiplication with the denominators $R,a>0$ leads to the quadratic equation (in a): $\;a^{2}=R^{2}-aR\;$
And the positive solution is: $\;a={\tfrac {R}{2}}(-1+{\sqrt {5}})$

Myosci (talk) 23:02, 9 December 2022 (UTC)[reply]

[1] Regular polytopes, p 93-95, regular star polygons, regular star compounds

[2] Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons p.36-38

[3] Weisstein, Eric W. "Polygram". MathWorld.

[4] Weisstein, Eric W. "Star polygon". MathWorld.

[5] Weisstein, Eric W. "Star figure". MathWorld.

[6] The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum, a {p/q} regular polygon can be transformed into {p/(p/2-q} by a continous sequence of intermediate isogonal polygons.

[7] *Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 246 (916). The Royal Society: 411. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. {{cite journal}}: Invalid |ref=harv (help)

[8] Coxeter, The Densities of the Regular polytopes I, p.43 If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consistents of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.

[9] Coxeter, Regular polytopes, 12.4 Petrie polygon, pp. 223-226.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]