Talk:Birefringence
| This It is of interest to the following WikiProjects: | |||||||||||||||||||||
‹See TfM›
| |||||||||||||||||||||
Image
[edit]I found the text in the current image ("Healthy Eating") to be rather distracting. I took a calcite crystal and took a different photo: http://commons.wikimedia.org/wiki/File:3310.calcite_%28Iceland_Spar%29_birefringence.jpg - would suggest switching to that or something similar. --Furrfu (talk) 17:30, 6 March 2010 (UTC)
.
[edit]The refractive index is referred to several times as a tensor. This is incorrect, because the property does not transform by the laws of tensors (although permittivity does). See for example "Modern Crystallography IV" Springer series in solid state science v.37, L. A. Shuvalov (Ed.) --FPD.
Could someone also include a discussion on how the ionosphere is birefringent for HF radio waves?
(No) Serious Errors in Mathematical Description
[edit]The description contains a very serious error in equation 3a
(3a)
This is not correct for anisotropic materials as it has used the assumption that the electric field vector E and the electric flux vector D are parallel. In fact, the whole point of anisotropic materials is that these vectors are not parallel to each other. See Born and Wolf. The author appears to have used an isotropic form of Maxwell's Equations in his derivation.
I'm taking the liberty of removing the entire section in question as it is seriously wrong. You should of course, consult a registered expert on this. 193.1.100.105 17:21, 26 October 2007 (UTC)
- Actually, my bad. Sorry. The epsilon mentioned was a tensor, not a scalar. The section actually seems fine. ObsessiveMathsFreak 00:29, 31 October 2007 (UTC)
Errors in formal definition
[edit]The "formal" definition section is wrong, I think, because it fails to take into account that the divergence constraint on the electric field is changed by the anisotropy: now we have . This means, among other things, that the electromagnetic wave equation has to be written in its full form , which does not simplify to if the electric field is not divergence-free.
The easy way to see the error is that the conclusion is absurd: if simply lies along one of the principal axes of ε, then for most directions of there will be no eigensolutions that satisfy the divergence constraint .
I don't have time to fix it now, but I tagged the article as disputed.
(By the way, the subsection on fibers is goofy too, because it mixes up nonlinearity and birefringence when the two have nothing to do with one another. It's also kind of obscurely written, because the semi-vectorial Schrodinger(-like, it's not quantum mechanics) equation is simply an approximation that can be used in low-contrast waveguides.)
—Steven G. Johnson 20:29, 16 December 2005 (UTC)
Sorry for the error in the definition - and thanks for pointing it out. Using the wave equation properly as you quote, I get , which then satisfies the divergence constraint. I will try to correct it, unless you do first.
- The "new" version comes to the same conclusion, and is still wrong. The solution electric fields for propagating waves are not simply eigenvectors of the dielectric tensor, nor are they restricted to propagate in only three directions in the crystal. There are propagating solutions in every direction, but the dispersion surface depends upon polarization. Again, you made the same mistake: equation (4a) does not follow from equation (3a) because the divergence of E is not zero. I suspect that you are doing something like commuting the ∇ and ε operations, which you can't do if ε is not isotropic. —Steven G. Johnson 18:57, 29 December 2005 (UTC)
Note that this problem is, I think, much easier to describe in terms of the magnetic field, since to use the electric field you must inherently solve a generalized eigenproblem (matrices on both sides) or a non-Hermitian problem if you move both matrices to one side. For the magnetic field, you get an ordinary eigenproblem:
with the constraint , where we have written the magnetic field as:
This is an ordinary 3×3 eigenproblem for , which is Hermitian if we neglect material absorption (i.e. if ε is Hermitian) and thus has three orthogonal solution vectors and corresponding eigen-frequencies ω. One of these solutions is ω=0 but violates the divergence constraint, so it is discarded. The other two solutions have magnetic fields orthogonal to k, and correspond to the propagating transverse waves. The corresponding electric field amplitude is given by:
The electric field amplitude is not in general orthogonal to , nor does it generally lie along one of the principal axes of ε. Nor are the two electric field polarizations orthogonal; rather, they satisfy .
Note also that k is the direction of the phase velocity, but is not generally the direction of the group velocity for anisotropic media, and it is the group velocity that determines the direction in which the refracted beams propagate. Note also that the "effective index" is not in general one of the three eigenvalues of , but rather lies in between the eigenvalues. (I seem to recall that it forms an ellipsoid, or at least an ellipse for each possible orientation of .
My own research involves media more complicated than simple homogeneous dielectrics such as this, so I'm probably forgetting some interesting details here, and there might be simpler analysis tricks. e.g. there seem to be all sorts of graphical methods for analyzing these birefringent systems that I've never looked into. But I think I can still spot erroneous approaches.
Note also that for a particular plane of incidence, the resulting solutions have a phase velocity that lies in the same plane, and I believe there are only two refracted solutions even when ε has three distinct eigenvalues. Hence the errors at trirefringence. (The reason that there are only two refracted solutions is obvious from above: for a particular k, there are only two eigenfrequencies corresponding to the two transverse polarizations. Correspondingly, in a given plane of incidence there are only two solution ellipsoids that can be coupled to.) This comes back to the basic misconception that the refracted rays do not in general lie along the principal axes nor are they polarized in those directions.
—Steven G. Johnson 20:27, 29 December 2005 (UTC)
- whoops - please check eqns 3-4 again. Do they not follow now? If is an eigenvector of n, then surely k is perpendicular to . A general can be written in the basis of these eigenvectors, so as far as I can see, they can then be treated independently. However, I now understand that that does not make them different rays. My use of birefringence is a lot simpler than this stuff, and I agree that your discussion is more sensible, so please edit as you see fit. User:salthebad Salman Rogers
- Your equation (4a) looks okay now (although 3a has a typo...the time derivative should be 2nd deriv). And yes, you can always write any vector in the basis of the eigenvectors of ε, but that's misleading because the eigenvectors of ε are not themselves solutions (except when k lies along certain directions), so they cannot be treated independently. (Because the polarization is not generally an eigenvector of ε, it is not in general orthogonal to k.) Because of this, your equation (7) and the subsequent discussion are wrong. The phase velocity is not given by c divided by one of the eigenvalues of √ε.
- I would want to look it up in a textbook or two before writing it up myself (I can't because I'm on vacation now). Not so much because I think my analysis is wrong, but there may be a more standard approach, terminology, and perhaps some algebraic tricks that I haven't seen. —Steven G. Johnson 01:36, 30 December 2005 (UTC)
Third time lucky... I hope! Birefringence is more complicated than I thought. My rewrite follows KD Moller Optics p238ff, and it should be correct although it is still not a complete description of course. —Salman Rogers
- It looks okay now, although I haven't checked the detailed algebra I assume it's okay since you took it from the textbook. It's a bit unsatisfying because I think you can't quite see the forest for the trees in this kind of approach (I think that's a common weakness of textbooks that dive into the component equations without investigating the higher-level algebraic structure of the problem), but it will do for now. Thanks for looking it up. —Steven G. Johnson 23:43, 5 January 2006 (UTC)
However, I should point out that there is one hidden assumption in the algebra as you presented it: you are assuming that the eigenvectors of ε are real and orthogonal. This is in general true only for materials in which absorption loss is negligible (or can be treated as a first-order perturbation) and in the absence of magneto-optic effects, in which case ε is a real symmetric matrix. Does your textbook comment on this? —Steven G. Johnson 23:51, 5 January 2006 (UTC)
- Thanks for your approval :-) I agree that component equations are not very satisfying, but in this case, I think the fact that they neatly end up with the isosurfaces of a sphere and ellipsoid multiplied together, is satisfying enough. As for absorption - the textbooks that I've seen, as well as research papers on optical anisotropy in liquids/soft matter generally reserve birefringence for retardation only (real n), and dichroism for any absorptive component. --Salman Rogers
More errors?
[edit]Hello. According to : (3a)
the is wrong. I just checked it out and I am sure. Any idea? with regards MSchwarz
- Looks right to me (neglecting material dispersion and assuming μ=1). and , so combining these two one gets . —Steven G. Johnson 03:06, 25 June 2006 (UTC)
Hi, MSchwarz again. Please have a look! (2.Maxwell) and with (1.Maxwell) (and and ) .....and there is no anymore...... furthermore you easily can get to the 'wave-equation' with the "großmann-Identität" (german-word, sorry, I dontknow): and as mentioned : (3.Maxwell: ! and )
which is : You`ll find it in any book. And that was the reason for getting into this. Im sure. Greetings from Hamburg, MSchwarz 05:51, 25 June 2006 (UTC)
- You assumed that , which is only true in vacuum. (c always denotes the speed of light in vacuum.) (If you're confused by the c factors in my explanation, above, it's because I was instinctively using cgs units. Actually, I tend to set all the dimensionful constants to unity, myself.) You also assumed that the medium was homogeneous (so that you could pull μ through the derivatives), which I did not, above. In your final equation, you assumed that the medium was not only homogeneous, but also isotropic, in order to get , which is definitely not the case here. —Steven G. Johnson 15:31, 27 June 2006 (UTC)
Birefringence values for ice
[edit]I suppose checking birefringence values for water ice. Now it stands: 1.309 1.313 +0.014 which are wrong, because 1.313-1.309=0.004, not 0.014. It looks like the mistake is copied from the source website. I have no idea of proper values, if someone has the sources - please check it.
Fiber Optic subsection.
[edit]On 16 December 2005, Steven Johnson wrote:
(By the way, the subsection on fibers is goofy too, because it mixes up nonlinearity and birefringence when the two have nothing to do with one another. It's also kind of obscurely written, because the semi-vectorial Schrodinger(-like, it's not quantum mechanics) equation is simply an approximation that can be used in low-contrast waveguides.)
This is Adrian Keister, and I wrote that section on fiber optics. I'm not quite sure I follow your comments.
1. I realize that nonlinearity and birefringence are not the same thing. In what way does the subsection mix them up? It is true that the coupled nonlinear Schrödinger equation takes birefringence into account and is thus a model for birefringence in a fiber optic cable, among other things. See C. Menyuk, Application of multiple-length-scale methods to the study of optical fiber transmission, Journal of Engineering Mathematics 36: 113-136, 1999, Kluwer Academic Publishers, Netherlands, for the derivation of the coupled nonlinear Schrödinger equations starting from Maxwell's equations, and applying the boundary conditions for a fiber optic cable.
- Nonlinearity and birefringence are independent physical concepts. Yes, you can have both in the same fiber, but there is no reason to include both here, and it is misleading to imply that you need to include nonlinearities in order to model birefringence.
2. The coupled nonlinear Schrödinger equations are called that because in applying the Inverse Scattering Transform, the forward scattering problem uses a Lax Pair and , and the operator is typically the Schrödinger operator. The eigenvalue problem, therefore, is the time-independent Schrödinger equation from quantum mechanics. There is thus quite a close link between the Inverse Scattering Transform and quantum mechanics. These equations are not called the coupled nonlinear Schrödinger-like equations.
- I'm quite familiar with what the NSE is, although I think your terminology is unneccessarily obscure (the standard terminology for the derivation can be expressed in four words: slowly varying envelope approximation = SVEA). In any case, you're not seeing the forest for the trees here. First, most readers will have heard of the Schrodinger equation in the context of quantum mechanics where it has a specific physical interpretation which does not apply here (the solution is not the quantum probability amplitude, the terms are not kinetic/potential energy, etcetera). The only reason for the name is that the linear part has the same form as the quantum Schrodinger equation, but it does not have the same interpretation. This confuses people if it is not presented carefully.
- Second, any mention of the NSE in this context is incomplete if it does not mention that it is only an approximation (a first-order approximation at that) for weak nonlinearities and slowly varying wave envelopes.
- In any case, semi-vectorial slowly-varying envelope approximations are simply one of many ways to model birefringence in optical fibers, and it's a bit strange to single them out here. (For one thing, that approximation, as applied in the linear or nonlinear Schrodinger equation, only models the effect of birefringence; in order to actually predict birefringence for a particular geometry or perturbation you need other methods.)
3. Naturally, since actual solitons do not exist, only a soliton-effect, no one is saying that the equations model the physical situation perfectly. But saying that the equations model the physical situation perfectly is not the same thing as saying that the equations model the physical situation.
- Why are you bringing up solitons? Again, a concept quite independent of birefringence. (FYI, the SVEA is only an approximation even in the linear case, too.)
4. I'm not sure why the fact that the coupled nonlinear Schrödinger equation is only an approximation renders the subsection "obscurely written."
I would appreciate any comments you might have in reply.
Regards, Adrian
Biological subsection
[edit]Can anyone comment on the role of birefringence in the eye?
Is the crystalline lens a multifocal lens?
Sapoty 06:50, 7 July 2007 (UTC)
Also - maybe someone who knows about synovial fluid analysis - for diagnosis of gout or pyrophosphate arthropathy - could add something here? Would be useful - this is probably the only application most medical students will find for birefringence.
Just a thought! (G) —Preceding unsigned comment added by 78.145.153.48 (talk) 08:53, 30 September 2008 (UTC)
Negative/positive birefringence
[edit]One reference is made to negative birefringence, in the context of microscopy. No other reference is made to birefringence having a polarity. Please could somebody explain the difference between -ve and +ve birefringence. —Preceding unsigned comment added by 87.80.19.201 (talk) 14:46, 6 January 2008 (UTC)
Collagen fibres are birefringent
[edit]Collagen fibres because of their anisotropic properties exhibits berefringency under polarised light. When collagen is stained with picrosirius red, the birefringency becomes even enhanced because picrosirius red posseses anisotropic property too.145.107.12.33 (talk) 13:52, 8 April 2008 (UTC)
Uncomprehensible
[edit]This article as it stands now is almost impossible to understand without a physics background. I wanted a way to explain birefringence to group of non scientists and got no help at all from the article. ping (talk) 04:24, 8 June 2009 (UTC)
Try http://simple.wikipedia.org/wiki/Birefringence —Preceding unsigned comment added by Furrfu (talk • contribs) 20:26, 23 April 2010 (UTC)
Unclear sentence in "Electromagnetic waves in an anisotropic material"
[edit]under "Mathematical description" the sentence:
"...., with a relative permittivity tensor ε, where the refractive index n, is defined by ."
is not clear to me. Perhaps a problem with bolds and non-bolds. I also think the comma after "where the refractive index n" shouldn't be there.
160.45.24.185 (talk) 12:16, 20 November 2009 (UTC)
True, there is a weird mix of fonts that puzzled me. But also, isn't there a big assumption at this point ? The usual expression of in the scalar case is . If we make the parallel with , then we see that we assumed (or identity matrix). Also, mix of absolute and relative. I don't know if it's a problem or not. Niriel (talk) 16:37, 8 August 2012 (UTC)
- The whole section assumes (relative permeability), because μ would otherwise show up in the eigenproblem too. However, at visible and infrared wavelengths there is almost always negligible magnetic response, so this is usually a valid assumption there. — Steven G. Johnson (talk) 18:38, 8 August 2012 (UTC)
- Ok! Then in the Maxwell-Faraday-Ampere equation () I'm fine with the with speed of light in vacuum and relative permittivity. I'm more confused with the in Maxwell-Gauss: with but that epsilon is not the relative permittivity, it's . Isn't an missing there? Niriel (talk) 08:46, 9 August 2012 (UTC)
some help at identifying the axes would be nice
[edit]This article does not clarify at all in its table where exactly the x, y and z axes lie with respect to the incident ray and the optical axis in the images. John Riemann Soong (talk) 05:31, 1 November 2010 (UTC)
Diagram wrong?
[edit]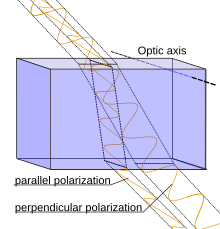
The diagram shows the parallel polarised light refracted more than the perpendicular polarised light, but the caption text says the opposite. Which way is it? -- cheers, Michael C. Price talk 09:07, 25 March 2011 (UTC)
- If it's this diagram, the caption was indeed stating what you said. It hopefully gives accurate information now, but I'd appreciate a little peer-review just in case. Mikael Häggström (talk) 04:50, 20 May 2011 (UTC)
- The caption below the diagram also refers to the parallel (s) and perpendicular (p) polarizations which is the incorrect nomenclature. (p) refers to the parallel polarization and (s) to the perpendicular polarization (s being derived from 'senkrecht', the German word for perpendicular) 1.128.97.77 (talk) 04:24, 3 May 2017 (UTC) Kim.
- IP editor, you're right, see Plane of incidence. ('s' and 'p' polarizations are so confusing in English...). It's possible the 'parallel' and 'perpendicular' in the figure are meant to be relative to the optic axis, however this is just adding even more confusion. --Nanite (talk) 15:31, 3 May 2017 (UTC)
Revert to what was given in source
[edit]I saw the edit [2] on positive versus negative birefringence, but reverted it to what was given by the source (ref name=McClatchey509). However, I'm not an expert on the subject myself, so if anyone would give a good reason for these changes, or provide a better reference, then I'd very likely change my mind. Mikael Häggström (talk) 04:42, 20 May 2011 (UTC)
Birefringence as a property or phenomenon
[edit]The first sencente now reads Birefringence, or double refraction, is the decomposition of a ray of light into two rays.... Birefringence is thus refered to as a phenomenon. I think the most common usage of the word is instead as a property of birefringent materials. E.g. Crystals possessing birefringence include...[[3]]. The lede section is about the phenomenon and referes to the property as the birefringence magnitude. The rest of the article on the other hand is all about birefringent materials and the anisotropy of the refractive index, not focusing on the phenomenon of splitting rays. I think the lede should be rewritten to reflect the topic discussed in the rest of the article. I intend to do so when I find time unless someone objects. Ulflund (talk) 17:17, 2 November 2011 (UTC)
- There are cases where the phenomenon occurs in a material that is not intrinsically birefringent, e.g. the Faraday effect. I think the ambiguity in language here is common - very often something that is considered a phenomenon in physics ("calcite exhibits birefringence") will be considered a property in materials science ("calcite is a birefringent material"). I think the lede is all right as it stands - it's in line with ScienceWorld's definition. The anisotropy of the refractive index is how birefringence is characterized, and the splitting of rays is one way it is commonly observed - I would say both are part of the definition, and if some parts of the article emphasize one more than the other, that's okay. Sho Uemura (talk) 23:20, 3 November 2011 (UTC)
- I agree that different sections should be allowed to emphasize phenomenon/property differently, but not the lede. The lede should reflect the article. As it is now the lede is about splitting of rays, and the rest of the article about anisotropic refractive index. Ulflund (talk) 17:13, 4 November 2011 (UTC)
- Looking in the What links here list for birefringence i notice that out of the first 20 pages all except Luminiferous aether referes to birefringence as a material property. [[4]] might be considered notable, and it makes a distinct difference between double refraction (phenomenon) and birefringence (property). — Preceding unsigned comment added by Ulflund (talk • contribs) 19:01, 6 November 2011 (UTC)
- All right, sounds good to me. Sho Uemura (talk) 12:29, 8 November 2011 (UTC)
- Looking in the What links here list for birefringence i notice that out of the first 20 pages all except Luminiferous aether referes to birefringence as a material property. [[4]] might be considered notable, and it makes a distinct difference between double refraction (phenomenon) and birefringence (property). — Preceding unsigned comment added by Ulflund (talk • contribs) 19:01, 6 November 2011 (UTC)
Peridot vs. olivine; uniaxial and biaxial vs. crystal system
[edit]I am a mineralogist, and while I am no expert on optical properties, I was surprised to see peridot listed as a uniaxial substance, but olivine listed as a biaxial one, for two reasons:
Peridot is the gem name for coarsely crystalline, pretty olivine. They are the identical phase. Their optical properties should not differ in such a fundamental way.
Every basic textbook on optical mineralogy, including every basic textbook on mineralogy with a chapter on optical (e.g., Klein and Dutrow 2007, Manual of Mineral Science 23rd edition, see p. 300), that I have seen states that uniaxial crystals are in the tetragonal, hexagonal, or trigonal/rhombohedral crystal systems; and biaxial crystals are orthorhombic, monoclinic, and triclinic. Are there really exceptions to this, and in particular, is there really a gemmy variety of olivine that is one, while most olivine is not? Def-Mornahan (talk) 16:30, 15 September 2012 (UTC)
- Removed peridot from uniaxial list. Thanks, Vsmith (talk) 21:40, 15 September 2012 (UTC)
Picture of an airbus windshield
[edit]The fringes observed on the airbus windshield is wrongly attributed to birefringence, event if it looks similar to a stressed polymer viewed through a polarizer. They are due to thin film interference caused by a conductive Indium Tin Oxide (ITO) thin film deposited on the window for electrical defrosting/defogging. The fringes are strongly visible because the thin film thickness is highly non-uniform on purpose : as the voltage is applied on two opposite points of the window, a uniform conductive film (uniform sheet resistance) would lead to non-uniform current density, and non-uniform defrosting. Some window parts, especially on the sides and far from the electrical contacts, would dissipate less heat, and defrosting would be significantly less efficient here. The ITO thickness pattern is cleverly designed to provide a rather uniform heat dissipation over the whole window.
I worked for 5 years in thin film R&D for the building & automotive industry, including conductive coatings. Now developing a polarized & thin film raytracer. — Preceding unsigned comment added by 88.164.16.51 (talk) 18:16, 10 June 2013 (UTC)
- Many thanks for your detailed correction. I will consequently move the picture to thin film interference article and change the caption accordingly. Etan J. Tal(talk) 21:01, 11 June 2013 (UTC)
- You're welcome! I saw the picture was removed from thin film interferences which has already too many pictures. It could be added to Indium Tin Oxide(ITO) which has no real life application picture. Also the article mentions many applications such as transparent electrode or EMI shielding, but never defrosting, while there are number of patents such as this one : http://www.patentstorm.us/applications/20080176084/description.html for ITO defrosting - Etienne
Biaxial materials table -- specific values given for solid solutions are ill-defined
[edit]The table that gives specific values of the indices of refraction α, β and γ for biaxial materials includes several solid solutions with compositional ranges: biotite K(Mg,Fe)3AlSi3O10(F,OH)2, muscovite KAl2(AlSi3O10)(F,OH)2, olivine (Mg, Fe)2SiO4, and topaz Al2SiO4(F,OH)2. But the indices of refraction of all these materials are composition dependent. Indeed, one way of measuring the composition of, for example, olivine (that is, it's Fe/Mg ratio) is to measure an index of refraction and use the well-known linear relationship between index of refraction and composition in this mineral.
In any case, this means the table values are ill-defined. Olivine (Mg, Fe)2SiO4 can have a value of α anywhere between 1.635 (pure Mg end member) and 1.825 (pure Fe end member), yet here a value is given to four significant digits as if it were a constant applicable to the whole solid solution series. In fact, for olivine the values given all correspond nicely to Mg0.95Fe0.05 composition (source: Deer, Howie and Zussman, An Introduction to the Rock-Forming Minerals, 2nd edition (1992), Longman Scientific and Technical (Essex, England)), which is an unusual but not extremely rare natural composition.
For topaz the three values gives all correspond to a particular specimen with about 19 weight percent F, but natural topaz ranges from ~14 to 20.7 weight percent fluorine.
For biotite and muscovite, the numbers given are within the ranges of natural specimens, but the point remains that these values go with a particular composition along the solid solution series, not with the entire family of compositions. Either that, or these are to be interpreted somehow as average or mid-point values of the range, but if so they should not be given to such high precision (the range, for example, for α for biotite is 1.530-1.625 (variation in 1st decimal place).
Solution: some indication needs to be given that these are example values corresponding to fixed compositions along the indicated solid solutions, or specific values need to be replaced with explicit ranges (this is how they are given in Deer, Howie and Zussman, a fundamental mineralogy reference), or as lower-precision values that can encompass the full range of values within the solid solution. — Preceding unsigned comment added by Asimow (talk • contribs) 20:57, 4 November 2013 (UTC)
Multiferroics
[edit]I have removed the following sentence and reference from the birefringence section in the refractive index article since it seemed to specialized. It might fit somewhere in this article though.
In materials simultaneously lacking time-reversal and spatial inversion symmetry (for example multiferroics), refractive indices can be different even for counter-propagating light beams, which effect is termed as directional birefringence.[1]
Ulflund (talk) 19:51, 25 August 2014 (UTC)
Assessment comment
[edit]The comment(s) below were originally left at Talk:Birefringence/Comments, and are posted here for posterity. Following several discussions in past years, these subpages are now deprecated. The comments may be irrelevant or outdated; if so, please feel free to remove this section.
| The article on birefringence as it presently stands is almost totally inaccessible to a non physicist. Even with a fairly extensive background in chemistry I simply could not understand it. Since I was looking for an explanation of birefringence that I could pass on to a group of non scientists it was no help at all. ping (talk) 07:24, 30 June 2008 (UTC) |
Last edited at 07:24, 30 June 2008 (UTC). Substituted at 09:43, 29 April 2016 (UTC)
- It's also no help at all to a scientist because it talks about birefringence, but never says what it is.
- What is birefringence? --2600:387:6:80D:0:0:0:57 (talk) 17:29, 31 July 2017 (UTC)
External links modified
[edit]Hello fellow Wikipedians,
I have just modified one external link on Birefringence. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:
- Added archive https://web.archive.org/web/20131214030317/http://homepage.ntlworld.com/w.amos2/Brad%20Amos%27s%20Website/BR1.pdf to http://homepage.ntlworld.com/w.amos2/Brad%20Amos%27s%20Website/BR1.pdf
When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).
This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).
- If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
- If you found an error with any archives or the URLs themselves, you can fix them with this tool.
Cheers.—InternetArchiveBot (Report bug) 02:45, 3 November 2016 (UTC)
Image that came through the Wiki Science Competition
[edit]
Leaving this image here in case editors of this page find it useful (the subject is far outside my wheelhouse, but I find it interesting, and the image striking). Uploaded by the creator for the Wiki Science Competition (it was one of the finalists in its category). The person who made it has a website explaining how he did it with some other nice images, for anyone interested. — Rhododendrites talk \\ 06:05, 26 January 2018 (UTC)
- B-Class level-5 vital articles
- Wikipedia level-5 vital articles in Physical sciences
- B-Class vital articles in Physical sciences
- B-Class physics articles
- Mid-importance physics articles
- B-Class physics articles of Mid-importance
- B-Class Geology articles
- Mid-importance Geology articles
- Mid-importance B-Class Geology articles
- WikiProject Geology articles
























































