Talk:Bell's spaceship paradox/Archive 5
| This is an archive of past discussions about Bell's spaceship paradox. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | ← | Archive 3 | Archive 4 | Archive 5 | Archive 6 |
Bell's Spaceship Paradox
Treat the combined system of two spaceships and the tether as a single unit. As seen from an oberver at rest the entire system contracts. As seen on the spaceships, there is no contraction. In either case, the tether cannot break. DrWhoJP 11:24, 18 September 2007 (UTC)
- That's not useful. Another way to state that the entire accelerating system contracts is to say that the front accelerates less than the rear in the frame of the launch pad. However, the Bell spaceship example/paradox is about identical rockets that equally accelerate. Harald88 16:27, 30 September 2007 (UTC)
- No, it's not about identical rockets that equally accelerate. It's about rockets that accelerate (differently) "such that they remain a fixed distance apart as viewed from the rest frame". That's not identical rockets with identical acceleration. Simanos (talk) 09:11, 5 December 2009 (UTC)
Comments Including a Descriptive Solution
Obviously, to have any meaningful discussion about Bell’s Spaceship Paradox it is important to have that discussion in reference to the correctly stated version of the paradox or, at least, with a common understanding of the paradox. While I didn’t research the wording of the paradox, the precise wording only appears to matter to the extent of stating that the acceleration of each spaceship is “measured by an onboard accelerometer.” According, I did not confirm the wording of the paradox in the Wikipedia article as being historically correct. Appropriately, my comments below are in reference to the paradox as stated and the article as worded on February 10, 2009.
- History: The whole point of the problem was to resolve the ambiguity concerning the reality of "Lorentz contraction" & time dilation. Right from the start in 1905, there was constant debate about how "real" the effects were. Although some authors wrongly asserted the effects were always physically real or some that they were merely apparent (a sort of "perspective" effect), the theorists mostly hedged about inbetween.
- Dewan & Beran came up with the beautifully simple and elegant "two rockets and string" scenario in order to (as they thought) prove Lorentz contraction to be physically real since apparent effects could obviously not snap strings.
- Consequently there are no "onboard accelerometers" in any original statements of the problem (or by Bell 17 years later). They are redundancies wheeled in by some commentators that only serve to confuse the issue. The problem simply requires the two rockets (or spaceships) to be absolutely identical and to have identical, unspecified acceleration programs. Like all seminal relativity problems or paradoxes, the observers should be able to explore the structure of their environment using the classic apparatus of measuring rods clocks and light signals.
- For purposes of synchronising clocks and for gauging rocket separation, the travellers must revert to inertial motion. There is no difficulty about this since, in order to preserve the "identicality" of the two rockets, they can simply cut engines either at identical (unadjusted) on-board clock times, or equivalently at identical fuel consumptions. They will then remain symmetrical to stationary ground observers, as required, but of course their own mutual measurements of synchronisation & separation will now differ from ground.
- Good to see this initiative as there seems to be a lot of wasted discussion on this page based on inconsistent "definitions" of the problem. From what I read in the article the basic assumption in the definition of the paradox is "that they remain a fixed distance apart as viewed from the rest frame". This is equivalent to the rockets having "identical, unspecified acceleration programs", again as measured from the rest frame of course! The calculation in the analysis section is based on this. It concludes that once the rockets reach terminal velocity the usual Lorentz contraction formula applies as expected. This means that in the frames of reference of the rockets the distance between them must have increased (by a factor gamma). This means that the string must have stretched (or if it is not sufficiently elastic, snapped) along the way regardless of the details of what happened in between. AlexFekken (talk) 14:45, 19 January 2010 (UTC)
My plan is to post the following discussion on the discussion page for feedback. Depending on the feedback I would expect to proceed with one of the following options: (1) revise my discussion, (2) post the solution in a section of the main article under the heading “Solution,” (3) create a new article titled “Solution to Bell’s Spaceship Paradox,” or (4) abandon my discussion because of a lack of any consensus.
The Paradox
Bell’s Spaceship Paradox is considered a paradox because there are seemingly conflicting answers to the question of whether the string will break depending on the approach and the method used to solve the problem. In brief, if the two equally accelerating spaceships and the interconnecting string are considered to constitute three co-moving elements of an accelerated frame of reference, then the expected length compression in the direction of travel would appear to affect all points, elements, and distances within the frame including both the two spaceships and the interconnecting string. Consequently, both the distance separating the two spaceships and the interconnecting string would appear to sustain equal compression, and the string would therefore not break. This view is seemly consistent with the view of an observer on either spaceship, where the observer would seemingly (though incorrectly) not expect to observe any change in the distance between the two spaceships or any change in the length of the interconnecting string.
However, if the two equally accelerating spaceships are considered to constitute two individual and separate accelerated frames of reference, then the length compression in the direction of travel would appear to affect each spaceship as a separate entity, but not the distance between them. Because the interconnecting string is initially being accelerated by the forward-positioned spaceship by virtue of being pulled (as opposed to being pushed by the rear-positioned spaceship), it will also exhibit length compression and therefore stretch and eventually break. This view is seemingly consistent with the view of a stationary observer where the observer views parallel trajectories for each spaceship maintaining a constant distance between them, but views compression in the length of the string. Accordingly, the relevant question in the paradox is which of these two opposing views, if either, is correct.
The Solution
Because the wording of the problem states that the acceleration of each spaceship is measured by an onboard accelerometer, the correct solution is that the string will stretch and eventually break. However, had the wording been different regarding what constituted equal acceleration, the answer could have been different. In the case as stated, because each spaceship is accelerated independently, the distance between them remains fixed as observed by a stationary observer, who also views the compression in the length of string and thereby logically concludes that the string will break. In contrast, observers on the two spaceships observe the distance between the two spaceships to increase thereby also providing a logical (but different) explanation for why they also view the breakage of the string.
Regarding onboard clocks, to a stationary observer the onboard clocks on both spaceships would remain in synchronization to each other. Furthermore, if the two spaceships are in radio communication, both the stationary observer and onboard observers would observe each spaceship to have a corresponding red shift or blue shift during their corresponding periods of acceleration. However, in contrast to the stationary observers, onboard travelers would observe their radio communication to become skewed and out of synchronization. The periods of observed red shift and blue shift would not be equal and signals would indicate that the clock on the other spaceship had shifted in time during the period of mutual spaceship acceleration. Stationary observers would also view this as an observation of the travelers thereby observing the travelers to view a loss of synchronization while the stationary observers would view synchronization of time being preserved.
An example is as follows: A traveler in the forward spaceship would observe radio or light transponder signals sent and received from the forward spaceship to indicate that the onboard clock on the rear spaceship was running slower (during the period of acceleration) thereby lagging or reading behind in time. In contrast, a traveler in the rear spaceship would observe radio or light transponder signals sent and received from the rear spaceship to indicate that the onboard clock on the forward spaceship was running faster (during the period of acceleration) thereby leading or reading ahead in time. Furthermore, all of this would appear logical to the stationary observer, but could appear nonsensical to traveling observers unless they rationalized the event from the perspective of the stationary observer and then transferred the event to their own frame of reference. This aforementioned skew is a consequence of the travelers experiencing acceleration.
- Thus far the explanation is broadly correct. The subsequent consideration of how to accelerate to preserve the string or clock synchronisation is largely irrelevant. What ought to be considered is how string breaking could occur if we repeat the scenario from a new inertial launch station that was co-moving with the rockets at some point in their travel. If two new identical rockets are simultaneously launched in the opposite direction to before from this moving inertial platform, the string must now get longer as the rockets accelerate and their "absolute" velocity decreases.
- As Dewan & Beran pointed out in their original 1959 paper, the reason the string must also now break is not due to physical contraction, but because the re-synchronised clocks used to launch "simultaneously" will actually launch the rocket pulling the string, slightly before the tail end rocket.
- This shows that although the "absolute" frame of reference cannot be identified in SR, it must exist and all reciprocal "contraction" and "time dilation" between relatively moving observers are an unquantifiable mixture of physically real, and merely apparent effects.
- Ultimately, it is obvious this must be so, as it is clearly mathematically impossible (and therefore also physically impossible) for both A>B and A<B to hold. Put simply, impossible for two rods to be physically shorter than each other, or two clocks to run slower than each other.
Furthermore, if the pilot of the forward spaceship adjusts the acceleration of the forward spaceship to compensate for the compression in length to thereby not break the string, he would have to accelerate at a lower rate and for a longer period of time (to achieve the same final velocity). To travelers onboard they would observe the onboard accelerometer displaying a lower rate of acceleration and the onboard clock displaying a longer period of acceleration. However, these observations would be completely consistent with observers who view the two spaceships as stationary in a uniform gravitational field. And, if educated in the general theory of relativity, the travelers would be aware that in the up-field spaceship the onboard accelerometer would be expected to read lower and the onboard clock would be expected to operate faster and thereby read ahead.
Accordingly, to preserve synchronization between the onboard clocks for both spaceships, the event must include two provisions not stipulated in the paradox. First, the forward spaceship must accelerate at a lesser rate than the rearward spaceship by an amount corresponding to that required to account for the length compression in the direction of travel. Second, the onboard clock on the forward spaceship must be slowed to a lower rate than the onboard clock on the rearward spaceship by an amount corresponding to that required for the different clock rates that occur in an equivalent gravitational field corresponding to the spaceship accelerations. If the two above provisions are accomplished, then the event as observed by the travelers would appear as if both spaceships were in a common gravitation field and the upper-positioned spaceship was simply adjusting to the known and understood gravitational effects of general relativity.
- I think those "provisions" need not be included or stipulated as they are a consequence of the problem statement that the distance as measured in the rest frame must remain the same. They merely spell out in more detail what the calculation of the Lorentz contraction at terminal velocity already shows us: that there must be relative motion between the rockets in their own reference frames and as a result that they cannot always be in the same frame of reference. The relative motion causes the string to snap. Incorrectly assuming that the rockets are always in the same frame of reference causes the paradox. AlexFekken (talk) 15:27, 19 January 2010 (UTC)
Lorentz Transformations
Regarding problems in using the Lorentz Transformations in solving the paradox, the Lorentz Transformations are simply inadequate to provide a solution to the paradox because they are inadequate to represent the transitions during periods of acceleration. Fundamentally, the transformations map distance and time for only two frames with one common point in time and one common point of position between them (normally origin). The subject paradox is represented by three frames having a coincident point in time, but two different points of position. Although the two spaceships have the same velocity (by one definition), they do not share the same moving frame in terms of t and x. Accordingly, although you can plug numbers into the Lorentz Transformations, discontinuities result. In fact, instantaneous changes in velocity cause corresponding instantaneous changes in positions and clock time in the transformed frame. Even large accelerations over small distances or small accelerations over large distances can cause huge discontinuities.
The Article
I found the Wikipedia article to be confusing. From my perspective the article appears to have a greater interest and focus in reporting the opinions of Dewan, Beran, Nawrocki, Matsuda, and Kinoshita than in clarifying the paradox directly. The article appears to provide the opinion that the solution to the paradox is unknown and that prominent physicists do not agree, hence the references to Dewan, Beran, Nawrocki, Matsuda, and Kinoshita.
Regarding my understanding of the paradox, although I certainly do not have any prominence or notoriety in physics, I didn’t find the paradox overly difficult to resolve (assuming that my explanation is correct). I also found numerous articles, tutorials, q and a’s, and class notes written by physics professors and physicists including Ph.D.’s that conclude what I explained above to be correct. Regarding the opinions of Dewan, Beran, Nawrocki, Matsuda, and Kinoshita, they may or may not have significance. I found that the references to them were typically journal articles to which I didn’t have cost free access, so I was unable to make any further assessment.
The Discussion
I am also confused by the long, detailed, and repeated discussions in this discussion section, especially between parties identified as Rod Bell and EMS, but also by Pjacobi, Harold88, and Pervect. I attempted to read and follow some of these discussions, but I simply did not have the time required. In brief, what I viewed were discussions based in some confusion over frames of reference, the consequences of acceleration, and an inability to apply the principles of the general theory of relativity. I simply do not have time to add clarification to each of these discussions. I did respond to a comment by Rick Crawford on 24 May 2008 in the section headed “Constant distance argument faulty!?”
Bill Wolf (talk) 12:55, 17 February 2009 (UTC)
- Hi Bill I'm just "passing by" (I rarely look at Wikipedia discussions anymore), but I can comment on an essential point. I see that you wrote "From my perspective the article appears to have a greater interest and focus in reporting the opinions of Dewan, Beran, Nawrocki, Matsuda, and Kinoshita than in clarifying the paradox directly. " Well, that is the essence of what wikipedia is meant to do - only provide facts of reputed opinions, and not do any WP:OR. If you want to "clarify the paradox directly" in Wikipedia, then you are required to first get a paper published in a reputed journal, and preferably wait until someone cites it (so that its notability is evident). Then your opinion is good enough to be included in Wikipedia. If this is not clear, please inform yourself with the info on the left of this page. Harald88 (talk) 09:51, 1 July 2009 (UTC)
Analysis
This is a funny analysis.
- You prove that that as observed from both spaceships, their distance L is always the same. This is right.
- No this is totally wrong. Perhaps you misunderstood the problem: the distance in the rest frame is constant, what happens in the moving frames is the question. AlexFekken (talk) 15:41, 19 January 2010 (UTC)
- You draw a spacetime diagram which illustrates this and includes an additional event B'' which obviously shows where the second spaceship will be some time after B' has occured.
- You draw a line connecting the events A' and B'' and assert that the earth is flat - oops, sorry - that this line shows the spaceships' distance as observed from a comoving frame, i.e. that in the comoving observer's spacetime the string is stretched.
- Never seen a space-time diagram with different frames of reference? Please check the textbooks. AlexFekken (talk) 15:46, 19 January 2010 (UTC)
- Then by some proper mathematics and presuming the assertion that the earth is flat - oops, sorry - that A'B'' is the spaceships' distance as observed from a comoving frame, you prove that this means the string is streteched in the comoving observer's spacetime.
- From this you conclude that the string will break.
Hey, are you kidding?
You assert something which is equivalent with "the string will break" (3), you prove that the assertion is equivalent to "the string will break" (4), and from this you conlude that your assertion has been right (5)?
THINK:
An "observer in a comoving frame" is the same like an astronaut going off-board and hovering near his ship with no relative movement to the ship. Now you say: As long as he is on-board, he sees the other ship at distance L, and as soon as he goes off-board, he suddenly sees it at Lɣ ? Oh dear, this is not Wikipedia, this is a voodoo show.
After acceleration, a second-ship-comoving observer has exactly the same future world line as the second spaceship! He is only displaced in y and/or z dimensions, but neither in x or in t! He will observe the first ship in synchronous time and at the same distance like someone on-board of the second ship, e.g. at an event A'' which is in the diagram at the same time and left hand of B''.
This whole analysis is nothing more but circular conclusions based on a wrong (or misunderstood) diagram. What is the source of this analysis? A textbook, or just proprietary WikiPhilosophy? Wikipedia should only include common knowledge, not private speculations. --217.87.150.69 (talk) 11:29, 14 November 2009 (UTC)
I've always found these graphs to be a wonderful way to completely duck things that can withstand a proof. That doesn't make this wrong, but throwing in the Lorentz Gamma for a length doesn't make overly much sense. If you have two objects, attached by a third object, that accelerate at a uniform rate, it is effectively a single body with a single acceleration rate. So long as the velocities used are reasonable (micrometeorite shields, for example, work on the principle that when moving faster than the speed of sound in its component materials an object tends to spend its energy in shattering rather than in elastic or even plastic deformation).
The fact that the same acceleration provides the same velocity means both are in the same reference plane, and as such no relativistic effect is seen and no relativistic factors are required.
Even were the observations of the position of the other craft incorrect, an observation of position is not the position. Because an ambulance sounds faster coming than going doesn't mean it actually is going faster.
If you took the theory that the bodies could be made into disjoint elements, then the strain of the change in length (where only a few microinches per inch will cause failure) would destroy everything at speed.
Given the hand-waving of Cerenkov Radiation and the need to drop to graphs to make any sort of statement about these systems, it seems our understanding is in its infancy and as such blanket statements of correctness are simply conjecture and theory until a suitable proof (mathematical or experimental) can be formed, rigorously tested, and defended against all better options.
Now, GPS satellites are already based on relativistic theory, if the production companies could be convinced to have their systems talk to other in-space systems in different orbits and have them share the data, then there would be empirical data to test against these theories, although the low velocity probably wouldn't give us enough resolution. Michael F (talk) 19:29, 22 April 2011 (UTC)
So do the ships accelerate equally or not? And is the observer moving with the ships?
I think those two things should be made more clear, the way it is now it is too easy to overlook details like this and get conflicting answers. --TiagoTiago (talk) 07:17, 5 November 2011 (UTC)
- An observer moving or not moving with the ships can't affect if the string breaks! Perhaps you mean that the different analyses should more clearly state from what perspective they are made? Apart of that, the article starts with:
- "both spaceships start to accelerate, in such a way that they remain a fixed distance apart as viewed from the original rest frame."
- Is that not clear enough? Note that "equal acceleration" is an observer-dependent statement. Harald88 (talk) 12:53, 19 January 2012 (UTC)
To quote from Bell's paper: "Three small spaceships, A, B, C, drift freely... Let ships B and C be identical, and have identical acceleration programmes. Then (as reckoned by an observer in A) they will have at every moment the same velocity, and so remain displaced one from the other by a fixed distance." The first point to make from this quote is that remaining a fixed distance apart is a conclusion (let...then...) from having identical acceleration programmes rather than an assumption. The second point is that this conclusion is inconsistent with special relativity: According to Special Relativity, the distance between two points in a moving frame will shrink as observed from a rest frame (one can quote Einstein's original paper as a reference for this). Einstein's version of the theory does not distinguish between points on material bodies versus points separating open space, whereas a theory based on contraction by forces within a material body does make such a distinction, giving rise to the continued arguments you see.
Alternatively, if we interpret Bell's example to mean that the two ships indeed maintain constant distance from one another in A's frame, then the ships could not be identical. The ship in front would have to accelerate more quickly (that is, use a more powerful engine), burn more fuel, etc. In this case, it is the higher rate of acceleration required to achieve the "constant distance in A's frame" that causes the string to break. While we could identify Lorentz-Fitzgerald contractions as the reason that the ship in front would need to burn more fuel to maintain "constant distance in A's frame", ultimately the string breaks merely because B is pulling away due to a more powerful engine burn, not because the string itself experiences Lorentz-Fitzgerald contraction. It is doubtful that Bell meant this interpretation as he seemed to carefully specify that the ships are identical and always have equal velocities, implying that he meant for them to remain in the same frame. Furthermore, talking of a single "comoving frame" makes sense only if both ships (B and C) are sharing a single frame, which would not be true in this alternative interpretation. Most likely, Bell himself simply made an error in his analysis in his effort to somehow prove that Lorentz-Fitzgerald contraction is "physical". — Preceding unsigned comment added by 68.65.71.90 (talk • contribs) 01:49, 17 February 2012
- The above unsigned remarks are absolutely correct !! Bell specifies pre-programmed identical acceleration profiles for the spaceships & from that draws the (wrong!) conclusion that they will remain a constant distance apart as viewed from stationary A's frame. Harald88 is wrong to modify the conditions to specify accelerations so "that they remain a fixed distance apart as viewed from the original rest frame". Because the distance between the spaceships would appear contracted to A in exactly the same way as the thread or any other solid length, unequal accelerations would be necessary to make them appear to A at constant distance - contrary to the statement of the problem !
- D.H. (below) also misunderstands the application of Special Relativity to the situation, not grasping the distinction between real, physical effects and merely "apparent" artefacts of the measurement process. To say that "by definition" the distance does not change (according to A), is to ignore the effect of SR on any measurement procedure. And to suggest that the rear ship must accelerate harder to stay the same distance behind, is absurd because the different accelerations of each ship as viewed from the other is a purely apparent phenomena due to the progressive disparity in the travel times of light from the front meeting the oncoming rear ship and light from the rear having to 'catch up' with the front ship. Indeed, Dewan & Beran even use the word "appear" as in - "the front rocket will not only appear to be a larger distance from the back rocket..."etc. If the rear spacecraft were actually to adopt a stronger acceleration than the front, it would sooner or later crash into the back of the front vehicle, in spite of any such misleading observations from the rear passengers ! Desiderata9 (talk) 00:22, 27 February 2013 (UTC)
...........
- There are two possibilities:
- a) The acceleration is simultaneous in A's frame, and thus changes in B/C's frame per relativity of simultaneity.
- b) The acceleration is simultaneous in B/C's frame, and thus changes in A's frame per relativity of simultaneity.
- Bell pointed out, that the spaceships had identical acceleration programs in A's frame, so that in this frame the distance between the rockets remains constant. Or as it was put by Dewan and Beran (1959): "If we suppose that at a prearranged time both rockets are simultaneously (with respect to S) fired up, then their velocities with respect to S are always equal throughout the remainder of the experiment..This means, by definition, that with respect to S the distance between the rockets does not change...This would appear differently to observers in various inertial frames along the track...It can be shown that as V increases, the front rocket will not only appear to be a larger distance from the back rocket with respect to an instantaneous inertial frame, but also to have started at an earlier time".
- In other words: In B/C's frame, and length L increases due to asynchronous acceleration (per Lorentz transformation and relativity of simultaneity), and becomes – the non-contracted spring breaks. Now, per length contraction this length L2' is shortened in A's frame by , and thus stays the same as before acceleration (of course, since in this frame the acceleration remains synchronous) – the contracted spring breaks. That's all. --D.H (talk) 11:06, 17 February 2012 (UTC)
- The above paragraphs seem a bit confused, so let's try and clarify things a little...
- Bell specifies identical acceleration programs, from which it follows that they will remain a constant distance apart according to A. There is no need for the forward ship to accelerate harder to achieve this in A's frame ! This is the point that Bell, and more particularly Dewan & Beran, were at pains to emphasize, since Nawrocki had made the same suggestion that distance between unconnected bodies should suffer Lorentz-Fitzgerald contraction. That this is impossible is easily seen by considering that the rear ship together with its time-distance trajectory can be 'slid forward' to replicate the starting position of the front ship, & translational invariance therefore implies the distance is constant throughout the acceleration.
- It is only in B&C's frames that the distance appears to increase, because from the rear ship, the front ship appears to have set off slightly earlier & clocks aboard the front ship appear to be going faster & faster (as light takes less & less time to travel from front to oncoming rear ship) & thus the acceleration program appears speeded up. Contrariwise, from the front ship, the rear ship appears to have set off slightly later & clocks aboard the rear ship appear to be going slower & slower (as light takes longer & longer to reach the front ship) thus making the rear ship's acceleration program seem retarded.
- It is worth remembering, however, that this scenario in no way "proves" the physical reality of Lorentz length contraction, since it is not known if the string actually would break (!!) - there being no experimental verification of relativistic length contraction in any case !
- [To be a little pernickety, I would point out that Bell refers to a "thread" and not "string", It was Dewan & Beran that envisaged two "rockets" connected with a "string"...] -H.C. 21 June 2012
- "Bell specifies identical acceleration programs, from which it follows that they will remain a constant distance apart according to A." No it doesn't. They only remain a constant distance apart in A's reference frame if you ignore Lorentz-Fitzgerald contraction, which this thought experiment is supposed to be about. All that Bell's argument demonstrates is that Bell (along with an awful lot of other physicists) doesn't understand Special Relativity. Clement Cherlin (talk) 03:57, 26 July 2012 (UTC)
- Clement Cherlin (above) is absolutely correct and Bell was completely wrong ! However, I'm not sure I agree that "an awful lot of other physicists" similarly don't understand SR, since as Bell admits, all his colleagues at CERN disagreed with him, as I believe most "proper" working physicists (as opposed to casual internet pundits) also dismiss Bell's purported string-breaking scenario. Desiderata9 (talk) 00:39, 27 February 2013 (UTC)
- Unfortunately, this OR has not yet been published by "reliable sources". But since the object of the Bell exercise is to examine the stresses on the thread, the nature of the structure joining the ships is irrelevant (thread/string/rope/strut, chemistry, ductility, fracture strain, etc.). So it can be considered to be a single ship with 2 engines, which makes the entire paradox not only obvious, but also ultimately irrelevant. The Bell problem's concepts can be faithfully reworded to examine the stresses within that ship whose single controller triggers & regulates both engines, and what an observer in an independent frame would perceive. The entire ship would appear to contract as a unit (Lorentz-Fitzgerald contraction with respect to ship A's frame), and there would be no internal stress to separate the engines from each other, as noted in comments above (constant separation with respect to S). This specifically contradicts a second condition of the Bell problem (appearance of constant separation), revealing the problem to have been poorly constructed, and of no educational value within the specific field of Special Relativity. It may serve as an educational tool for logic. Steve8394 (talk) 05:12, 16 January 2013 (UTC)
- ....
- It appears the contributor above, Steve 8394, has not understood the point of Bell's (or rather Dewan & Beran's) thought experiment. It cannot be replaced by "a ship with 2 engines" because the intention is to suggest that the space between two identically moving objects does not exhibit Lorentz contraction. Therefore in a sense the thread is irrelevant and could be dispensed with so that one simply considered two identical spaceships. Historically, since there has never been any direct empirical evidence of length contraction, many physicists considered such contraction may be merely an apparent artefact of measurement resulting from the necessity of using two separated clocks synchronised in a relatively moving inertial frame. Many standard textbooks on SR were ambiguous about whether Lorentz length contraction was physically real or an apparent "perspective effect of motion". The Bell/Dewan & Beran set-up is intended to show the physical reality of length contraction by contrasting it with the lack of contraction of the space that separates a pair of identically moving objects. A flimsy thread is chosen so as not to interfere at all with the motion of the two ships, yet itself exhibit contraction resulting in an unambiguous rupture.
- However, that being said, it's as well to bear in mind that the "thought experiment" actually proves nothing ! That is to say -
- (1) It is merely ASSUMED that the spaceships stay a constant distance apart in A's frame, there is no consideration of how this might actually be measured, which would of course be the exact same procedure as would be used for measuring the length of a moving solid object, and would therefore not necessarily yield a different result !
- (2) It is also ASSUMED that the thread will exhibit contraction in A's frame, and the conclusion that such contraction that may be observed must be physically real, depends on assumption (1) and the consequent snapping that ought to occur as the thread is "stretched" to span a greater distance than its physical length.
- ....
- The upshot is that the whole thought experiment does not in fact advance, much less resolve, the doubt and ambiguity surrounding the reality or otherwise of Lorentz length contraction. Desiderata9 (talk) 22:23, 9 February 2013 (UTC)
- Unfortunately, this OR has not yet been published by "reliable sources". But since the object of the Bell exercise is to examine the stresses on the thread, the nature of the structure joining the ships is irrelevant (thread/string/rope/strut, chemistry, ductility, fracture strain, etc.). So it can be considered to be a single ship with 2 engines, which makes the entire paradox not only obvious, but also ultimately irrelevant. The Bell problem's concepts can be faithfully reworded to examine the stresses within that ship whose single controller triggers & regulates both engines, and what an observer in an independent frame would perceive. The entire ship would appear to contract as a unit (Lorentz-Fitzgerald contraction with respect to ship A's frame), and there would be no internal stress to separate the engines from each other, as noted in comments above (constant separation with respect to S). This specifically contradicts a second condition of the Bell problem (appearance of constant separation), revealing the problem to have been poorly constructed, and of no educational value within the specific field of Special Relativity. It may serve as an educational tool for logic. Steve8394 (talk) 05:12, 16 January 2013 (UTC)
- We have to distinguish between two questions: a) whether the spring breaks or not (as far as I know, most publications agree in that the spring will break); and b) whether this result proves length contraction to be "real" or not (there is actually some controversy in reputable sources regarding this latter question, see Petkov and Franklin). PS: Since the start times and the acceleration programs are the same in S, then of course the distance in this frame remains the same. --D.H (talk) 13:24, 28 February 2013 (UTC)
Too many other things to read?
There us currently a complaint against the last section of this article, advising: "removing excessive, less relevant or many publications with the same point of view". Is this request reasonable in the case of a paradox that seems not to be resolved to general satisfaction? Or will readers need to see, in more detail, how people with expertise have tried to deal with the problem?P0M (talk) 16:15, 20 January 2012 (UTC)
- Apart of several links to apparently not peer-reviewed Arxiv papers it looks fine to me. For sure the list is not excessive, nor are there too many. Relevance as well as source quality must be the issue, generally Arxiv papers don't fulfill those criteria. I suggest to remove those links and the complaint Harald88 (talk) 09:33, 9 February 2012 (UTC)
Lack of clarity. Due to translation?
There seems to me to be a lack of clarity in this article. What exactly is the paradox? Does the string break when we expect that it should not, or does it not break when we expect that it should? Why should we expect the string to break, or not? What does it actually due in the (adequately) defined circumstances and why?
We also have phrases like (my italic), 'Bell reports that his colleagues at CERN disagreed with him, including a consensus of the theory division there, who asserted the string would not break'. What does that mean? It looks to me like it is the result of a translation from a different language. Martin Hogbin (talk) 10:32, 6 April 2013 (UTC)
- I assume you are referring to the introduction only. Dewan and Beran were very precise in answering those questions in the following section. But let's make some arrangements. --D.H (talk) 11:15, 6 April 2013 (UTC)
- The lack of clarity is not only in the lead. Nowhere in the article is there a clear and simple explanation of exactly what the paradox is and its resolution. We should have somewhere near the start of the article:
- 1) A clear description of the setup.
- 2) A simple exposition of the natural line of argument that leads to an erroneous conclusion.
- 3) A simple exposition of the line of argument that leads to the correct conclusion.
- 4) An explanation of where the error lies in the first line of argument.
- I think we have 1 in the article. The two spaceships are defined have equal accelerations in the starting frame and therefore they maintain a fixed distance between themselves as measured in the starting frame. As I understand it, in these circumstances, the thread breaks and this is the generally accepted correct answer.
- 2 seems to be completely missing. I imagine that the simplest argument is that in the rest frame of the accelerating spaceships nothing is happening is there is no reason for the thread to break.
- 3 is in the article but it is not clearly identified as the correct argument.
- 4 seems to be discussed to some degree in the last paragraph where Born rigidity is discussed.
- We also have the line, ' an informal and non-systematic canvas was made of the CERN theory division', which I do not understand. Martin Hogbin (talk) 19:10, 6 April 2013 (UTC)
- Point 2 is discussed at the end of the Dewan-Beran section: For instance, at first thought one assumes that length contraction should affect the distance between the spaceships the same way as the string, thus no breaking should arise (included now in the lead). Point 3 is stated several times: One only has to think that the proper distance increases due to relativity of simultaneity in the comoving frame S', thus the string breaks; and in the start frame S one applies length contraction on this steadily increasing length, so the spaceship distance remains the same while the string contracts. Yes, point 4 concerns Born rigidity, also alluded to at the begin of the analysis section - but it is also addressed in the Dewan-Beran section. Regarding the "canvas of opinion": according to Bell it was used to make the survey at CERN. I've rephrased it. --D.H (talk) 20:14, 6 April 2013 (UTC)
- You are rather missing my point. I am not saying that anything is incorrect but that the article is not immediately clear. Starting with point 2, for there to be a paradox, the incorrect argument should be simple and natural, almost 'obvious'. That is not the case in the article. Your statement is much better and clearer, that at first sight 'length contraction should affect the distance between the spaceships the same way as the string'. That is exactly the kind of statement that we should have in the article. It should also come before the correct argument, so as to create a paradox.
- Point 2 is discussed at the end of the Dewan-Beran section: For instance, at first thought one assumes that length contraction should affect the distance between the spaceships the same way as the string, thus no breaking should arise (included now in the lead). Point 3 is stated several times: One only has to think that the proper distance increases due to relativity of simultaneity in the comoving frame S', thus the string breaks; and in the start frame S one applies length contraction on this steadily increasing length, so the spaceship distance remains the same while the string contracts. Yes, point 4 concerns Born rigidity, also alluded to at the begin of the analysis section - but it is also addressed in the Dewan-Beran section. Regarding the "canvas of opinion": according to Bell it was used to make the survey at CERN. I've rephrased it. --D.H (talk) 20:14, 6 April 2013 (UTC)
- I agree that 3 is in the article but we should make sure that it is identified as the correct argument. This is currently not clear. The reader should not have to work it out for themselves.
- Finally, we need to show exactly how the erroneous argument fails. Why does the space between the ships not shrink - because it is defined not to.
- I suggest that we have an 'Introduction' section at the start of the body with a clear description of the paradox and its resolution in simple language. Martin Hogbin (talk) 21:04, 6 April 2013 (UTC)
- I have just reworded the section in the lead to make the English more natural and to make clear that the CERN conclusion was wrong. What do you think? Martin Hogbin (talk) 21:13, 6 April 2013 (UTC)
- Looks fine! Please continue to make it clearer. --D.H (talk) 21:26, 6 April 2013 (UTC)
Proposed introduction
I suggest a short introduction along the lines given above (refs to be added):
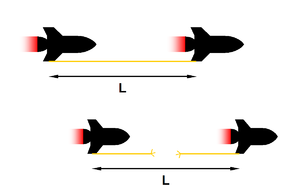
Dewan and Beran stated the thought experiment by writing: "Consider two identically constructed rockets at rest in an inertial frame S. Let them face the same direction and be situated one behind the other. If we suppose that at a prearranged time both rockets are simultaneously (with respect to S) fired up, then their velocities with respect to S are always equal throughout the remainder of the experiment."
At first sight many scientists have argued that the thread will not break. Both rockets and the thread all move at all times with the same velocity in the inertial frame S and are therefore all subject to the same Lorentz contraction. It is argued that entire assembly is contracted in the S frame thus the thread will not break.
This argument, however is incorrect. Dewan and Beran continued, "This means, by definition, that with respect to S the distance between the two rockets does not change even when they speed up to relativistic velocities."
The space between the spaceships does not undergo Lorentz contraction because, in the frame S it is effectively defined to remain the same length. The thread, on the other hand, being a physical object, maintains the same length in its own rest frame (proper length) and therefore must be Lorentz contracted in frame S. The thread therefore must break.
I think this explanation is based closely enough on the references not to be considered OR. What do you think?
I do start by slightly misdirecting the reader in order to establish the paradox , which we later resolve.— Preceding unsigned comment added by Martin Hogbin (talk • contribs) 10:13, 7 April 2013
- Some things are quite good, but I think it's little bit too detailed for the introduction. Also note that a fundamental issue of this article is the existence of relativistic stresses, and the increase in proper length between the rockets. I've included another version, using some of your wording. Please make improvements and clarifications. --D.H (talk) 11:14, 7 April 2013 (UTC)
- My suggestion was for a short 'Introduction' at the start of the body of the article rather than a replacement for the lead, which should be a summary of the article as a whole. You have incorporated my suggestion into the lead. My main concern was to cover the paradox aspect of the subject which is now done. Martin Hogbin (talk) 14:55, 7 April 2013 (UTC)
- Just out of interest, the simplest explanation of why the thread should break is, in my opinion, that the distance between the ships has a fixed coordinate length in the S frame (by definition), and thus the proper distance between the ships must increase with speed whereas the thread maintains a fixed proper length (because it is a physical object) and thus its length as measured in the S frame must decrease with speed. Do you agree? Martin Hogbin (talk) 15:27, 7 April 2013 (UTC)
- Exactly! --D.H (talk) 17:16, 7 April 2013 (UTC)
- NO ! Not 'exactly' at all !
- The real reason there are so many difficulties with formulating the explanation of this "paradox" is that it is trying to establish a conclusion that is simply not true ! The 'paradox' is false because there is in fact NO reason why the string should break ! The whole misunderstanding is caused by confusion between the two different & distinct forms of relativity - the earlier Lorentz-Poincaré-Fitzgerald version in which length contraction is real & physical, and the Einstein 'Special Relativity' in which due to reciprocity, length contraction is merely apparent & caused by clock (mis)synchronisation.
- There is further confusion between actual physical distances & lengths, and observed distances & lengths, in particular "proper" length or distance DOES NOT necessarily mean actual physical length or distance - the word "proper" is repeatedly misused in both the article and the talk.
- So, whilst by definition of setup, the distance between the spaceships remains constant, that does not mean that observers aboard the vehicles cannot be misled into thinking that they have moved further apart because of the effect on light signals exchanged between them during acceleration. In this case the "proper" distance, meaning the distance measured by on-board observers, is illusory & does not represent the real physical distance, which of course is constant in all frames.
- Similarly, in the 'stationary' launch frame S, there is no reason why there should be any distinction between on the one hand, the distance between the spaceships, and on the other hand, the distance between the ends of the string. To put it even more clearly, if the string was only attached at the front & not at the rear, but allowed to trail behind just touching the rear spaceship - there is no reason why any gap should open up between the rear end of the string and the rear spaceship ! This is because in SR, whether there is any "contraction' observed in either the distance between the ends of the string, or the distance between the spaceships (these being equivalent lengths), is entirely dependant on the method & procedure of measurement, in particular on the synchronisation of clocks at the two locations necessary to determine the positions of the ends "simultaneously". Any such measurement must give the same result for either the string or the spaceship distance - and if 'contracted' does not reflect the real physical distance !
- This is all because length contraction in Special Relativity is purely "apparent" & NOT physically real ! Such apparent, non-physical effects cannot give rise to real physical string-breaking ! Desiderata9 (talk) 16:41, 12 June 2013 (UTC)
- There are hundreds of real physical manifestations of the effects of SR. Do you have any reliable sources to say that you are right? Martin Hogbin (talk) 17:10, 12 June 2013 (UTC)
- It's notable that even those who say that length contraction is not "real" or "physical", know that the string will break and that relativistic stresses will arise, see Petkov and Franklin. This is a simple consequence of the Lorentz transformation for the special case that the distance doesn't change in the start frame. --D.H (talk) 19:19, 12 June 2013 (UTC)
- There are hundreds of real physical manifestations of the effects of SR. Do you have any reliable sources to say that you are right? Martin Hogbin (talk) 17:10, 12 June 2013 (UTC)
- Exactly! --D.H (talk) 17:16, 7 April 2013 (UTC)
Look, it would help a lot if people would take the trouble to read the original sources, and to understand SR properly before asserting opinions about this 'paradox' ! For instance, Martin Hogbin above queried the statement that J.S.Bell conducted a (not very systematic) survey of the CERN Theory Division & a clear consensus emerged that the string would NOT break, imagining it might have been translated from another language ! In fact the statement is a direct quote by Bell himself (who worked at CERN) in his article about the 'paradox' as reprinted in his well-known book "Speakable & Unspeakable in Quantum Mechanics". Furthermore, the meaning is perfectly clear - that the overwhelming majority of the CERN Theory Division (of leading physicists in the world mind you !), disagreed with Bell & disputed that the string would break ! It is worth bearing this in mind together with the fact that Bell also admits in his article that he prefers the older "Lorentz-Poincaré-Larmor" relativity theory to the SR of Einstein !! (And it is of course the older Lorentz etc theory that he uses to analyse the problem)
When people say that SR has been experimentally verified hundreds of times etc etc, in fact this is not true ! What is 'verified' each & every time is merely the Lorentz transformation relationship - which was known before Einstein came along - and even then only the time dilation & mass increase, but never any experimental or observational support for length contraction. An essential feature of Einstein's SR is "reciprocity" resulting from the equivalence of inertial frames, and this feature has never had ANY experimental or observational verification, but it does definitely imply that relativistic length contraction must be non-physical & purely a consequence of 'relativity of simultaneity' with regard to the setting of separated clocks necessary to measure lengths of moving objects. Or alternatively, a moving clock which is slowed in rate relativistically will show a shorter elapsed time to traverse a given stationary distance & therefore indicate the given distance to be shortened by exactly the 'contraction' predicted by Lorentz's equation - without obviously anything having physically happened to the stationary distance ! So 'length contraction' emerges as a non-physical, 'apparent' consequence of time dilation !
That length contraction in SR must be non-physical is easily proven beyond any doubt by the simple thought experiment of having identical spaceships depart from a back-to-back position (no string this time !) & accelerate in diametrically opposite directions for a while, then slow to a stop and reverse direction, accelerating back to the starting point so as to pass by each other closely at relative speed 2V, having cut engines just beforehand so as to become 'inertial'. Then, because of the completely symmetrical setup & identical but opposite pre-programmed flight schedules, the classic SR situation of inertial observers in relative motion has been reproduced whereby SR predicts observers aboard each spaceship will measure the moving lengths of the other spaceship to be shorter than their own - but since we have ensured they must be identical, the 'contraction' is therefore necessarily not physical but merely an apparent artifice of the measurement procedure ! Desiderata9 (talk) 12:01, 13 June 2013 (UTC)
- As explained above, your philosophical problems with the word "apparent" distracted you from the most important thing in relativity - learning to apply Lorentz transformations. There is agreement in almost all English publications (after the initial criticism of Nawrocky) that the string breaks (Romain (1963), Evett (1972), Bell (1976), MacGregor (1981), Cornwell (2005), Flores (2005), Styer (2007), Redzic (2008), Peregoudov (2009), Redzic (2009), Gu (2009), Petkov (2009), Franklin (2009), Fernflores (2011) Kassner (2012)). Only some non-mainstream physicists (Field) and some relativity beginners or antirelativists in internet forums still dispute the result that the string will break. However, in the peer reviewed literature, there is agreement that the string will break, and that is the only thing that counts in WP (WP:Sources, WP:OR, WP:Undue). --D.H (talk) 08:19, 18 September 2013 (UTC)
- I see, so the truth doesn't count !? Hmm maybe that's why Wikipedia has such a low reputation for reliability...
- The fact is that all those 'authors' you mention do not apply the Lorentz transformation correctly. Like you, they only use the spatial coordinate half and omit transforming the time coordinate, thus leading them to erroneously conclude that the string breaks.
- { I make a partial exception of John Bell, who confesses in his article, as well as elsewhere ["The Ghost in the Atom"- PCW Davies & JR Brown (C.U.P.1986 & Canto 1993) Ch.3 pp.48-51], that he doesn't believe in the Special Relativity of Einstein & prefers the earlier aether theory of Lorentz, Fitzgerald & Poincaré ! So by your criteria, John Bell would qualify as a 'relativity crank'...} Desiderata9 (talk) 13:31, 20 September 2013 (UTC)
Improvements to make?
- What a pity that D.H., who clearly has not understood Special Relativity, in particular that the reciprocity between observers in the theory implies that for instance "length contraction" is a purely apparent (and not physical) phenomenon arising from the measurement process, has chosen to rewrite the Bell Spaceship page in a biased way so as to suggest that the view of Bell et.al. that the string breaks, is correct, when most leading physicists (especially those who unlike Bell specialise in application of SR) have generally taken the opposite view.
- The fact is that Bell, like Dewan & Beran and other obscure commentators, either did not grasp, or did not accept Special Relativity as formulated by Einstein, but preferred to adhere to the older aether-based theory of Lorentz, Poincare and Larmor, (as Bell explicitly states in his book), which is why they regard relativistic contraction incorrectly as a physical shrinkage and thus conclude erroneously that the string will break. Desiderata9 (talk) 01:32, 1 March 2013 (UTC)
- 1) Only include statements that are properly sourced in the article. 2) We have to distinguish between two questions: whether the spring breaks or not (as far as I know, most publications agree in that the spring will break, including the PhysicsFAQ); and whether this result proves length contraction to be "real" or not (there is actually some controversy in reputable sources regarding this latter question, see Petkov and Franklin). 3) Regarding "aether": See Petkov and Franklin, who explicitly denied the notion of Lorentz's aether, but also stated that the string will break due to unequal acceleration in the rocket frames. 4) Generally: One simply has a frame in which two objects move at the same velocity, thus by definition their mutual distance doesn't change. A simple application of the Lorentz transformation shows, that during or after acceleration, the proper length between thos objects has increased in the object's new frame. --D.H (talk) 10:25, 1 March 2013 (UTC)
- It is manifestly completely & utterly wrong to claim that the proper distance between the spaceships increases - simply considering the flights of each vehicle independantly in the initial stationary launch frame shows that were the rear vehicle to be given any higher initial acceleration than the front, however small an increment, it would eventually overtake the front one !! That is simple, obvious and incontrovertible. It is mindless foolishness of the highest order to just blindly follow the application of equations without ever giving any thought to what they mean or represent in physical terms !
- Incidentally there are numerous authoritative sources in the literature, not to mention standard textbooks, that make it clear that relativistic length contraction is merely an apparent effect and that the only "reality" to be attributed to it is to the measurements obtained in the measuring procedure. Hence the well-known analogy with perspective effects where an object diminishes the further away it is - it can be 'measured' as smaller but of course has not in any way changed its physical size - an effect that like length contraction is also reciprocal !
- [ Also the connecting filament is a "string" and not a "spring" :) ] Desiderata9 (talk) 16:19, 1 March 2013 (UTC)
- Incidentally there are numerous authoritative sources in the literature, not to mention standard textbooks, that make it clear that relativistic length contraction is merely an apparent effect and that the only "reality" to be attributed to it is to the measurements obtained in the measuring procedure. Hence the well-known analogy with perspective effects where an object diminishes the further away it is - it can be 'measured' as smaller but of course has not in any way changed its physical size - an effect that like length contraction is also reciprocal !
- Regarding length contraction: Even people like Petkov and Franklin, who don't believe in the "reality" of length contraction, are (of course) the opinion that the string will break. As long as the acceleration and thus the distance remains the same in S, the proper distance in S' must increase, which is a trivial consequence of the Lorentz transformation. The only thing that remains to clarify is, whether both length contraction and acceleration (Dewan & Beran, Bell, Evitt etc.) are necessary to understand the breaking of the string, or whether only acceleration counts, not the "apparent" length contraction (Petkov, Franklin).
- Regarding Born rigidity and invariable proper length in S': Contrary to your assertion, the rear rocket will never reach the front rocket in S. The Lorentz transformation shows that at close approximation to light speed, the rocket distance becomes extremely Lorentz contracted in accordance with L=L'\gamma in S (assuming invariable proper length in S'), but this distance never becomes zero, thus L > 0 as long as L' > 0. Now, the corresponding difference in acceleration between the rockets accordingly decreases as well. If this goes to infinity, then the difference in acceleration practically vanishes completely near the speed of light (no big surprise, it's a limiting velocity in relativity), thus the rockets are practically moving with the same velocity and the difference between L' and L stays the same as well. The rear rocket will never have the acceleration required to reach or even overtake the front rocket. --D.H (talk) 11:20, 6 April 2013 (UTC)
- Sorry but this is utter rubbish ! The "proper distance" between the spaceships does not & cannot possibly increase ! Petkov et al & D.H. are talking nonsense when they suggest it does ! Consider: the spaceships are given identical flight programmes such that they accelerate identically from points a strings length apart in the direction of travel. This means that at any time in the duration of flight of one spaceship, "translational invariance" dictates that the other spaceship will have reached a point the same distance away from the first spaceship as they were when launched. That is to say that the time/distance trajectory of either spaceship is translationarily invariant & can be moved forward or backwards without altering its acceleration profile. The "proper distance" thus remains the same !
- However, it is true that during acceleration, light from the rear spaceship will take progressively longer to reach the front spaceship because it is accelerating away & thus the rear spaceship will APPARENTLY be falling behind, as seen from the front spaceship. Contrariwise light from the front spaceship will take progressively less time to pass to the rear spaceship which is accelerating towards it. This does not mean, as Edmond Dewan speciously argues in his 1962 response to Nawrocki, that because the front spacecraft (in his case a rocket) "seems" to be using fuel at a faster rate, it will "appear" to be 'pulling away' from the rear spacecraft. On the contrary, it means the front spacecraft will subtend a progressively larger angle, as seen from the rear one, & therefore "appear" to be getting closer !
- The fundamental errors that give rise to this supposed "paradox" are firstly a naïve & inappropriate application of the Lorentz transformation, & secondly the confusion between purely "apparent" effects & physically real changes. Thus the non-physical effects described by Dewan (& Beran) regarding how the spacecraft (rockets) "appear" or "seem" to one another, cannot possibly give rise to stresses in a string connecting the two that is stationary with respect to them & therefore of constant length.
- Thus it is clear that while the "proper distance" between the spaceships remains constant, the rear spaceship "appears" to be falling behind (& clocks etc aboard it appear to be going slower) as seen from the front spaceship, & contrariwise from the rear spaceship, the front spaceship "appears" to be getting closer whilst clocks etc aboard it "appear" to be running faster. Desiderata9 (talk) 02:51, 16 September 2013 (UTC)
- No, all of this has been explained to you (or User:Rod Ball, which is evidently your previous account) several times. "Identical" flight programs of course only lead to identical distances if (and only if) the board clocks and thus the board computers are working simultaneously. Well, you certainly heard about the circumstance that the Lorentz transformation leads to relativity of simultaneity – thus only in S the rockets start at the same time and thus their mutual distance stays the same, though in S' they are not synchronized, thus they are accelerating differently and the distance chances. This is so trivial that I can hardly believe that someone cannot understand this....
- Second, it's not a "naive" use of the Lorentz transformation, it's actually the most trivial case of all possible Lorentz transformations. In case you cannot handle accelerations, simply wait after the acceleration is finished and subsequently perform your transformation. Since you certainly don't dispute that the length is unchanged in S, a simple Lorentz-transformation from S to the new rest frame S' provides you with the unambiguous result that the rest length in S' became larger, which of course is only another way to express the circumstance that the acceleration wasn't simultaneous in S' in the first place. Everyone who denies this, also denies the applicability of the Lorentz transformation in the most simple case between two IS in relative motion...
- You also don't understand the meaning of the word "apparent" in the context of the principle of relativity. It doesn't mean that the predictions of relativity have no real consequences, but it only means that the description of those real consequences depends on the chosen frame. For instance, in this paradox, the length of the string is shorter than the distance between the rockets in all frames of reference, as it can be easily seen in a Minkowski diagram. The word "apparent" only comes into play, if you describe this real difference in terms of specific inertial frames - because in S this difference in length is due to the "apparent" increase of the rocket distance, while in S' it is due to the "apparent" contraction of the string. It seems that your philosophical problems with the word "apparent" distracted you from the most important thing in relativity - learning to apply Lorentz transformations and subsequently to learn what is "invariant" or "absolute" and what is "relative" or "apparent" in relativity.
- Of course, there is agreement in almost all English publications (after the initial criticism of Nawrocky) that the string breaks (Romain (1963), Evett (1972), Bell (1976), MacGregor (1981), Cornwell (2005), Flores (2005), Styer (2007), Redzic (2008), Peregoudov (2009), Redzic (2009), Gu (2009), Petkov (2009), Franklin (2009), Fernflores (2011) Kassner (2012)). Only some non-mainstream physicists (Field) and some relativity beginners or antirelativists in internet forums still dispute the result that the string will break. --D.H (talk) 08:13, 18 September 2013 (UTC)
- First brief response: No, I'm afraid it is yourself D.H., who does not understand how to apply the Lorentz transformations correctly ! You claimed in the analysis section that the 'proper' distance in S' between the spaceships had increased to gamma L. Not so ! You merely calculated the coordinate distance in S' between them.
- Open any textbook on Special Relativity & look up "proper distance" - you will find that it is defined as ds^2 = dx^2 + dy^2 + dz^2 - (cdt)^2 !! I simply corrected the analysis to calculate the true 'proper distance' in S' between the spaceships, which is L.
- What you have naïvely overlooked is that in S' the coordinate time difference between the spaceships at A' and B' has become gamma Lv/c^2 as the elementary Lorentz transformation shows ! You seem to think that in S' the forward spaceship is at B", but it has not reached there yet ! The dotted line in the diagram is just a coordinate line of simultaneity & happens to cross the inertial trajectory of B at B".
- Transforming from S to S' does not magically "teleport" spaceship B from B' to B" !! Desiderata9 (talk) 09:26, 18 September 2013 (UTC)
- Listen, S' is the new rest system of the rockets after the acceleration is finished. Why is this so hard to understand? So if you perform a Lorentz transformation of points A and B, from system S (where the ships are moving with v after acceleration) to S' (where they are at rest after acceleration), you are calculating the endpoints of resting objects in S', thus you have the rest length of the objects and the distance between the endpoints. And what do the Lorentz-Trafos tell us? Well they unambiguously show that the distance between A and B (again, those are the coordinates of the endpoints of in S' resting objects) has increased as compared to the coordinate length between A and B in S. Of course, this is in perfect agreement with relativity of simultaneity, which shows that the spaceships started at different times in S', thus they had different accelerations...
- Summarizing, it is easier to start in S': 1) You have two endpoints A and B with different (non-simultaneous) accelerations in S', therefore they are moving away from each other in S', and after the acceleration the distance of the now resting objects has increased, and the string has been stretched. 2) Of course, one can also choose frame S in which (by the Lorentztrans.) the accelerations are simultaneous and therefore the distance "appeared" to be the same compared to the start. (Actually, one should abandon the word "appear" in relativity, it serves no purpose and only distracts one from correctly applying the Lorentztransformation.)
- Dewan, Beran, and Bell unfortunately started with 2) and only afterwards they arrived at 1), so they had to focus their attention mostly on S and on length contraction, which caused much confusion by some readers. But the paradox is much easier to understand if one (like Petkov and Franklin) starts with 1) and then look at 2).
- BTW: As explained above, modern authors understand the paradox very well, and some of them even try to confirm it experimentally ("Bell's spaceship paradox in electron interferometry", arXiv:1309.1157). --D.H (talk) 10:21, 18 September 2013 (UTC)
- Nope ! You're still not correct ! You are confused by the distinction between "coordinate distance" and "proper distance". It really is quite simple & can be found in any relativity textbook ! The first sentence of your comment above is correct and perfectly in accord with what I've been saying - the two spacecraft at A' & B' are inertial and at rest in the system S', although they are moving at speed v in system S. However from this point is where you start going wrong !
- (a) We are not considering the "endpoints" or "lengths" of "objects" here - we are dealing with two independant identical spacecraft a distance L apart in S, and considering the distance they will be apart in the system S'.
- (b) The 'Lorentz transformation' consists of two parts - a spatial equation and a time equation. To perform a Lorentz transformation correctly from the coordinates in S to the coordinates in S' requires both transformation formulae to be carried out ! (You have only done half of the Lorentz transformation for the spatial coordinates alone !)
- (c) The true "proper distance" between the spacecraft at A' & B' in the system S' is equal to: sqrt[(dx')^2 - (cdt')^2]. This fundamental formula can be found in any textbook on relativity !
- (d) Although dt = 0 in the system S, so that in S the "proper distance" is equal to the spatial coordinate distance, dx = L, this is not the case in the system S' !! In S' a time differential arises between the spacecraft equal to: gamma.vL (using units in which c=1 for convenience) so that: dt' = gamma.vL.
- (e) Thus the "proper distance" between the spacecraft in S' is equal to: sqrt[(gamma.L)^2 - (gamma.vL)^2] = gamma.L.sqrt(1-v^2) = L ...which is correct because the "proper distance" is an invariant, independant of the observer's coordinate system !
- The article is therefore wrong in suggesting that the 'proper distance' between the spacecraft has increased ! (I notice incidentally that you've at least conceded in your comment that it is only the "coordinate length" between A & B that has increased to gamma.L -all you have to do now is to include consideration of the 'coordinate time difference' !) Desiderata9 (talk) 13:42, 18 September 2013 (UTC)
- a) Of course we are talking about "objects", which also applies to the distance between them. Look: Both ships are resting in S', therefore the distance between them (in empty space) is as constant as the ship's length. If it's easier to understand, use the word "rest length", which is defined as the "proper distance" between two events if they are measured simultaneously in the object's rest frame. The rest length between the two ships is increasing - while the rest length of the string is not increasing, it breaks.
- b) Keep in mind, we are transforming into the rest system of the spaceships. Think about the meaning of the word "rest". This means that A and B are, after the acceleration, always at the same location in S'. Therefore we do not need to perform an additional time transformation, the spatial transformation alone suffices. In other words: The condition of simultaneous measurements is only necessary in S, where the ships are moving (so what you call "coordinate length" only applies to the "contracted" length). It's different in their new rest frame S' - since the ships are at rest there, we can measure the distance whenever we want, they will always be at the same place.
- c), d), e) are thus wrong too.
- You really should believe what Flores, Franklin, Petkov, etc. wrote, they are correct. --D.H (talk) 14:08, 18 September 2013 (UTC)
- Now you've veered into total balderdash ! ...Have you ever studied relativity ? Because it doesn't sound like it from the comments a) & b) !! You are even contradicting yourself whilst stating exactly what I said as if you were contradicting me !
- In a) you say (I quote): "Both ships are resting in S', therefore the distance between them (in empty space) is as constant as the ship's length." Which, if you're referring to 'proper distance' & excepting I don't refer to the (irrelevant) ship's length, is exactly what I've been saying ! The proper distance between them, that you want to call "rest length" is indeed constant !
- Then you immediately contradict yourself by saying: "The rest length between the two ships is increasing" !!! This is of course a ridiculous statement - the "rest length", like what I prefer to call the 'proper distance', is constant, as you said beforehand.
- As for b), I agree that S' is the system in which the spacecraft are at rest (so system S' is moving at speed v with respect to system S), but it is complete nonsense to say that we do not need to use the time part of the Lorentz formulae when transforming between frame S and frame S'. Frames S and S' are in relative motion so the full Lorentz transform is necessary !
- You say, rather bizarrely, that "simultaneous measurements [are] only necessary in S, where the ships are moving", but this is absurd ! Whilst in frame S, the time aboard each spacecraft remains synchronised both during and after acceleration (by virtue of the identical setup & translational invariance) - from the point of view of frame S' they become increasingly out of sync during acceleration, due to 'relativity of simultaneity'.
- So although the spatial coordinate distance increases from L to gamma.L, so also does the time coordinate difference increase from zero to gamma.vL.
- Consider the diagram... the dotted line extending to B" is the 'line of simultaneity' with A' in frame S', so it is clear that the forward spacecraft at B' is NOT simultaneous with A' in the frame S'
- It really isn't that difficult to grasp ! Try and get hold of a relativity textbook that shows the 'squeezing' of coordinate grid squares into diamond shapes for frames in relative motion and it might become conceptually clearer... Desiderata9 (talk) 16:01, 18 September 2013 (UTC)
- No, the rest length remains constant after acceleration when it comes to rest in the new rest frame (this is what I referred to), into which we can transform with a spatial Lorentz transformation (for the reasons given above). Though this new rest length is of course not the same as the length during the asynchronous acceleration phases, and it's of course not the same as the rest length before the asynchronous acceleration. It's evidently fruitless to repeat all the reasons to you, why the rest length has been increased due to acceleration, it's all explained above and in the references (Dewan, Flores, Petkov, Franklin, the PhysicsFAQ, etc.). I'm not responding to you anymore on this talk page, though I will monitor the article very carefully! --D.H (talk) 16:29, 18 September 2013 (UTC)
So you prefer to remain deluded rather than understand how to properly carry out Lorentz transformations ! It's quite clear that the spacecraft have the same (horizontal) time coordinate as each other in frame S throughout their trajectories before, during & after acceleration. If you look at your own diagram you can see that in the frame S' where the time coordinate 'lines of simultaneity' are slanted upwards parallel to the dotted line, the spacecraft A' & B' no longer have the same time coordinate ! This corresponds to the conversion from t to t' when transforming from frame S to frame S'. Perhaps you should think about why you're neglecting a non-zero part of the Lorentz transformation !
As regards the dubious & obscure references (mostly unreliable non-peer-reviewed internet sources), I'd like to remind you of a well-known quotation from Richard Feynman, who said: "Science is the belief in the ignorance of experts" ! Desiderata9 (talk) 18:17, 18 September 2013 (UTC)
SIMPLE PROOF THAT YOU ARE WRONG !! ...about not needing the Lorentz time transformation:
Now D.H., if as you claim, the distance between the spacecraft dx' in frame S' is gamma.L at simultaneous time dt' = 0, then it ought to be possible to transform back from S' to S and retrieve the original dx = L and dt = 0 in frame S, should it not ?
Well let's try it out...
dx = gamma(dx' - vdt') = gamma(gamma.L - 0) = gamma^2.L ...WRONG !
(using units where c=1)
Now according to you, since the spacecraft are moving in S, we must also use the time formula:
dt = gamma(dt' - vdx') = gamma(0 - v.gamma.L) = - v.gamma^2.L ...WRONG AGAIN !!
Now let's try the same reverse transformation using my result of dt' = gamma.vL :
dx = gamma(dx' - vdt') = gamma(gamma.L - v.gamma.vL) = L.gamma^2(1-v^2) = L ...CORRECT !
dt = gamma(dt' - vdx') = gamma(gamma.vL - v.gamma.L) = 0 ...CORRECT AGAIN !!
Thus your notion that the time component of the Lorentz transformation from S to S' is not needed, because A' & B'are already simultaneously at rest in frame S', is irrefutably shown to be COMPLETELY WRONG !
Desiderata9 (talk) 01:47, 19 September 2013 (UTC)
- This is not a forum where you can "refute" or "prove" theories or ideas. Please go to a real forum (such as Physics Forums or scienceforums), where they might help you clarifying concepts such as "proper distance between two events", "proper length of a resting object", "contracted length of moving objects", etc. Sources especially published in the last decade in peer reviewed journals such as American Journal of Physics, European Journal of Physics, Physics Education, etc., agree that the rest length will increase:
- Dewan, Edmond M. (May 1963). "Stress Effects due to Lorentz Contraction". American Journal of Physics 31 (5): 383–386. Bibcode:1963AmJPh..31..383D. doi:10.1119/1.1969514
- Evett, Arthur A.; Wangsness, Roald K. (1960). "Note on the Separation of Relativistically Moving Rockets". American Journal of Physics 28 (6): 566–566. Bibcode:1960AmJPh..28..566E. doi:10.1119/1.1935893.
- Romain, Jacques E. (1963). "A Geometric approach to Relativistic paradoxes". American Journal of Physics 31 (8): 576–579. Bibcode:1963AmJPh..31..576R. doi:10.1119/1.1969686.
- Evett, Arthur A. (1972). "A Relativistic Rocket Discussion Problem". American Journal of Physics 40 (8): 1170–1171. Bibcode:1972AmJPh..40.1170E. doi:10.1119/1.1986781.
- Gershtein, S. S.; Logunov, A. A. (1998). "J. S. Bell's problem". Physics of Particles and Nuclei 29 (5): 463–468. doi:10.1134/1.953086.
- Tartaglia, A.; Ruggiero, M. L. (2003). "Lorentz contraction and accelerated systems". European Journal of Physics 24 (2): 215–220. arXiv:gr-qc/0301050. doi:10.1088/0143-0807/24/2/361.
- Cornwell, D. T. (2005). "Forces due to contraction on a cord spanning between two spaceships". EPL (Europhysics Letters) 71 (5): 699–704. Bibcode:2005EL.....71..699C. doi:10.1209/epl/i2005-10143-x.
- Flores, Francisco J. (2005). "Bell's spaceships: a useful relativistic paradox". Physics Education 40 (6): 500–503. Bibcode:2005PhyEd..40..500F. doi:10.1088/0031-9120/40/6/F03.
- Semay, Claude (2006). "Observer with a constant proper acceleration". European Journal of Physics 27 (5): 1157–1167. arXiv:physics/0601179. doi:10.1088/0143-0807/27/5/015.
- Styer, Daniel F. (2007). "How do two moving clocks fall out of sync? A tale of trucks, threads, and twins". American Journal of Physics 75 (9): 805–814. Bibcode:2007AmJPh..75..805S. doi:10.1119/1.2733691.
- Jürgen Freund (2008). "The Rocket-Rope Paradox (Bell's Paradox)". Special Relativity for Beginners: A Textbook for Undergraduates. World Scientific. pp. 109–116. ISBN 981277159X.
- Redžić, Dragan V. (2008). "Note on Dewan Beran Bell's spaceship problem". European Journal of Physics 29 (3): N11–N19. Bibcode:2008EJPh...29...11R. doi:10.1088/0143-0807/29/3/N02.
- Peregoudov, D. V. (2009). "Comment on 'Note on Dewan-Beran-Bell's spaceship problem'". European Journal of Physics 30 (1): L3–L5. Bibcode:2009EJPh...30L...3P. doi:10.1088/0143-0807/30/1/L02.
- Redžić, Dragan V. (2009). "Reply to 'Comment on "Note on Dewan-Beran-Bell's spaceship problem"'". European Journal of Physics 30 (1): L7–L9. Bibcode:2009EJPh...30L...7R. doi:10.1088/0143-0807/30/1/L03.
- Gu, Ying-Qiu (2009). "Some Paradoxes in Special Relativity and the Resolutions". Advances in Applied Clifford Algebras 21 (1): 103–119. arXiv:0902.2032. doi:10.1007/s00006-010-0244-6.
- Miller, D. J. (2010). "A constructive approach to the special theory of relativity". American Journal of Physics 78 (6): 633–638. arXiv:0907.0902. doi:10.1119/1.3298908.
- Fernflores, Francisco (2011). "Bell's Spaceships Problem and the Foundations of Special Relativity". International Studies in the Philosophy of Science 25 (4): 351–370. doi:10.1080/02698595.2011.623364.
- Kassner, Klaus (2011). "Spatial geometry of the rotating disk and its non-rotating counterpart". American Journal of Physics 80 (9): 772–781. arXiv:1109.2488. Bibcode:2012AmJPh..80..772K. doi:10.1119/1.4730925.
- Regards, --D.H (talk) 12:59, 6 October 2013 (UTC)
- It's no good listing references - it can't alter the mathematical facts ! What I was trying to point out above (perhaps with ill-tempered impatience, which was inappropriate), is that Lorentz transformations form a mathematical 'group', and that as such every element must have an inverse. So if Λ is a Lorentz transformation such that (x',t') = Λ(x,t), there must exist an inverse Λ̃ such that (x,t) = Λ̃(x',t'). Just using a "partial" transformation of the x-coordinate & ignoring the time coordinate transformation as you and many of the references have done, is illegitimate and represents an improper transformation that has no inverse ! Desiderata9 (talk) 19:07, 9 October 2013 (UTC)
Improvements to make? (old)
There are some discussions here above that suggest that the article lacks clarity. Perhaps with minor editing the text can be improved.
For example the first, rather technical picture in the "Analysis" section has nothing to do with the basic and easy to understand elaboration of Dewan and Beran's analysis. That's confusing to say the least, so I'll move that picture lower to near to the corresponding text.
What other improvements should be made?
Also, someone (Evanh2008?) put an "Original Reasearch" tag above the article with reference to this Talk page, but as far as I can tell, there's no motivation for it given here. In particular which parts of the text appear to lack references? Harald88 (talk) 11:00, 18 October 2011 (UTC)
- As nobody backup up the motivation behind that tag (to the contrary, there was criticism about citing reliable sources instead of doing original research), I will now remove it. Harald88 (talk) 12:44, 19 January 2012 (UTC)
- The "Analysis" section is not merely unclear, but is simply nonsense ! Whether or not the distance between the spaceships contracts or not is not established - it is merely assumed that it doesn't, and whether or not the string itself contracts or not is also not established but merely assumed that it does contract, both as considered from the "stationary" observer's point of view. The whole thought experiment is a red herring that proves nothing (apart from the possible gullibility of physicists).
- Rather than point out the elaborate way the assumptions are unconsciously smuggled into the analysis, may I invite readers to consider the following alternative scenario....
- Instead of the identical spaceships setting off in the same direction, do away with the thread and let them set off in opposite directions for a considerable time, and then reverse their direction of motion so as to arrive back at the starting point from opposite directions at very high speed. Now they will pass each other such that according to SR, observers aboard each spaceship will measure the other spaceship to be contracted compared to their own. However, this is physically (& logically) impossible because the symmetry of the situation means the spaceships are at all times physically identical ! - THEREFORE in this case any observed or measured "contraction" must be 100% APPARENT, & NOT physically REAL!! Desiderata9 (talk) 23:18, 9 February 2013 (UTC)
- Of course it is established that the distance remains the same in S (see Petkov, Franklin etc.). When you have one frame S, in which both objects have the same velocity and acceleration all of the time (note that it is totally irrelevant how this is achieved, whether by pre-programming, or by coincidence etc.), then of course their distance remain unchanged in S. And then it's a trivial application of the Lorentz transformation to show, that the proper length between two objects became larger in the new object's frame S'. --D.H (talk) 10:37, 1 March 2013 (UTC)
Yes it is a trivial application of the Lorentz transformation, but contrary to your erroneous statement the transformation in fact shows that the 'proper distance' (= physical distance) between the spaceships remains precisely the same as it was at launch ! An even simpler way to see this is to notice that the 'rear' spaceship need not be launched from a distance L behind the front one, but can instead be launched from exactly the same spot as the front spaceship a time L/v later ! After the identical acceleration period it will follow the same inertial trajectory as the 'rear' spaceship in the problem. This way however it is obvious that it must follow an identical trajectory to the front ship, having been launched from the same position a time L/v later. Therefore its physical or 'proper' distance from the other spaceship must be the same in a co-moving frame (or any other frame) as in the launch frame. The spaceship does not 'know' whether it was launched first or second so cannot know whether to 'pull away' or 'fall behind' !
Of course in fact it does neither ! Desiderata9 (talk) 20:25, 5 October 2013 (UTC)


