Talk:Autoregressive model

Summary and Better Examples?

This article is noticeably more difficult to comprehend than many other Wiki entries on statistics. A higher level summary statement on AutoRegressive techniques could be useful, especially example usages that point the reader in the right direction (ARMA, ARCH, ....) .

Strawman example of opening statement: Autoregressive models are used for prediction and data smoothing, especially in time-series data containing signal noise(SNR), moving averages(ARMA), and characteristically different time periods(ARCH). AutoRegressive (AR) models are linear combinations of the input parameter values and white noise values.

As an example, consider an input dataset with two parameters, time and power. We want to predict how much power we need to provide in the next second. Some noise exists in the power measurement, but we dont know exactly how much. We also know that real power usage varies considerably, for example during peak usage periods vs off-peak energy usages. Using an autoregressive model, we can learn from previous instances and predict the next power value. (Picture of example) — Preceding unsigned comment added by 208.127.244.182 (talk) 00:22, 30 November 2012 (UTC)

Stationarity conditions

Perhaps this has been addressed before, but could someone confirm that the stationarity condition here is correct? I think it is currently wrong so I'm going to change it. Shouldn't the roots of $P(z)=z^{p}-\phi _{1}z^{p-1}-\ldots -\phi _{p}$ have modulus less than one; and the roots of $Q(z)=1-\phi _{1}z-\ldots -\phi _{p}z^{p}$ have modulus greater than one?

e.g. for the AR(1) model

$P(z)=z-\phi _{1}$

has a root at $z=\phi$. We require this root to be less than one for stationarity.

I think there may be several instances of confusion involved here and in the current article text. First, from my understanding (yes, I am always learning): (wide-sense) stationarity is a property of certain processes, stability is a property of certain models. Second, I have looked up the referenced pages 88 and 90 in Shumway and Stoffer and a bit more. Page 90 deals with MA models, not AR models, which we are concerned with here. Third, while I do not quite fully understand Shumway's and Stoffer's seeming identification of explosive processes with non-causal ones on page 88, I do follow their explanation on pages 88 and 89 starting from equation (3.12) and leading up to the conclusion that $|\phi _{1}|<1$ is a condition for stability. Fourth, I think that for an AR model one does not (usually) apply the notation $\Phi (z):=\textstyle 1-\sum _{i=1}^{p}\varphi _{i}z^{p-i}$ (which, I seem to glean, with a plus-sign rather than a minus-sign may rather apply to MA models), but $\Phi (z):=\textstyle 1-\sum _{i=1}^{p}\varphi _{i}z^{-i}$ instead (with $p$ removed from the exponents).

Therefore, I intend to change the article text accordingly (with an eye to correction). Any motivated objections?Redav (talk) 12:10, 11 July 2020 (UTC)

Constant term

Some of the formulas include the constant term:

$X_{t}=c+\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}.\,$

while other formulas don't:

$X_{t}=\sum _{i=1}^{p}\varphi _{i}X_{t-i}+\varepsilon _{t}.\,$

I think the article should be consistent in the notation. Albmont (talk) 18:26, 18 November 2008 (UTC)

You're absolutely right. Personally I have never encountered the constant term outside of Wikipedia, but that's just me. --Zvika (talk) 06:43, 19 November 2008 (UTC)

gretl includes the constant term (optionally). So does R (programming language), as in fit.ar.par. But both softwares include anything in the "deterministic" component. Albmont (talk) 12:21, 19 November 2008 (UTC)

Well, then, definitely go ahead and put it in. --Zvika (talk) 13:39, 19 November 2008 (UTC)

Hey, just wanted to revisit this topic again since I started trying to create inline citations for this article. I found one source with a definition with the constant term but I seem to find a lot more sources without the constant. For example, in Shumway & Stoffer's Time Series Analysis and its Applications, they do not use the constant. Same for Box, Jenkins, and Reinsel's Time Series Analysis: Forecasting and Control as well as Time Series Analysis: Univariate and Multivariate Methods by Wei. I also do not see a constant used in Brockwell & Davis's Introduction to Time Series and Forecasting. I might be missing something but I believe that the definition for an AR model should not include a constant since most textbooks do not.

I want to see if anyone else has any strong opinions against this change though since it might ruffle some feathers and in case I'm missing something obvious. I'm planning on changing it if no one has any objections though. Moon motif (talk) 03:08, 28 August 2022 (UTC)

I think a problem with the constant term is that the equations for wide-sense stationarity involving the poles of the time-shift polynomial are no longer applicable. Consider the AR(1) model with the constant $c$ term. Assuming some nonzero initialization for the sequence, it's trivial to expand the sequence at a given time and use a geometric series to show that

$\mathbb {E} [X_{t}]=c{\frac {1-\phi ^{n}}{1-\phi }}+\phi ^{n-1}X_{0},$

which varies with $n$ but converges to $c/(1-\phi )$ in the limit. In other words, for the system to be wide-sense stationary, $c$ must equal zero. This result is compatible with Exercise 1.6 in "Adaptive Filter Theory" (4th Ed.) by Simon Haykin, which states that the input to an AR(1) must have zero mean. I believe this is an error in both this article and the general ARMA article. — Preceding unsigned comment added by 152.3.43.164 (talk) 18:02, 11 March 2013 (UTC)

Autocovariance or autocorrelation?

According to http://en.wikipedia.org/wiki/Spectral_density the spectral density is the FT of the autocorrelation (and according to my notes!) but here it is stated that it is the FT of the autocovariance. In the case there μ = 0 it doesn't affect the result, but is it right? If so can someone clarify the apparently contradicting information? —Preceding unsigned comment added by 163.1.167.139 (talk) 22:43, 21 March 2009 (UTC)

Gretl

Apropos gretl, I just noticed that when gretl computes the parameters in the AR(1) model with a constant term, it returns const and phi_1 based on equation $X_{t}=c+\varphi (X_{t-1}-c)+\epsilon _{t}\,$ instead of $X_{t}=c+\varphi X_{t-1}+\epsilon _{t}\,$. Albmont (talk) 17:05, 19 May 2009 (UTC)

Variance of X_t

The variance of X_t should be only valid for the assymptotic case, when t goes to infinity. That value is valid for a finite t in X_t only when we have a process that begins at t = minus infinite; in most real-world applications (for example, Monte Carlo simulations of AR(1) series), we begin with a fixed X₀ and, depending on phi and sigma, we may never get even close to the assymptotic values. Albmont (talk) 13:47, 9 October 2009 (UTC)

At least in the textbooks that I use, an AR process is defined as one which begins at negative infinity (e.g., Porat's "Digital Processing of Random Signals"). This is required to ensure that the process is wide-sense stationary. Almost all of the text of the article would change if you were to change this definition. For example, it would no longer be possible to talk about the autocovariance of the process or its spectral density. --Zvika (talk) 14:20, 9 October 2009 (UTC)

Maybe it could be possible to get a compromise. Let's write non-assymptotic equations for the conditional AR(1), namely X_t|X₀ - or even X_t|X_s, t > s. I think these formulas are more useful (for the sake of Monte Carlo analysis) than the assymptotic equations for a hypothetical series that begins at t = -infinite. Albmont (talk) 14:26, 9 October 2009 (UTC)

I don't object to that in principle, if it is stated in addition to the existing formulas, say in a separate section on conditional properties. --Zvika (talk) 15:25, 9 October 2009 (UTC)

OTOW, the current version of the article implies some inconsistencies. Because it says that AR(1) = random walk for φ = 1 (this is true only when X₀ is zero), also it allows an AR(p) even when the coefficients have a unit root (or worse). Maybe it should be better to keep the analysis of the stationary process with |φ| < 1 and t beginning at -infinite at a separate section too. Albmont (talk) 16:07, 9 October 2009 (UTC)

(outdent) OK, I was not aware of the fact that a random walk necessarily equals 0 at time 0, but apparently this is what it says in the random walk article, so I reworded that part. I still maintain that the standard definition of an AR process begins at -infinity. Do you have a source that says something else? --Zvika (talk) 08:55, 10 October 2009 (UTC)

State space form

AR(p) model $X_{t}=\phi _{1}X_{t-1}+\phi _{2}X_{t-2}+\cdots +\phi _{p}X_{t-p}+\varepsilon _{t},\;t\geq p$ where $\varepsilon _{t}\sim N\left(0,\sigma ^{2}\right)$

$X_{t}=X_{t},\;t<p$

The usual estimation method doesn't full use the data points t=0,...,p-1. Introduce the state space form, and to some extent, we can use these data points in a better way.

define $e_{1}^{'}=\left({\begin{array}{cccc}1&0&\cdots &0\end{array}}\right),E_{t}^{'}=\left({\begin{array}{cccc}X_{t}&X_{t-1}&\cdots &X_{t-p+1}\end{array}}\right)$

$G=\left({\begin{array}{ccccc}\phi _{1}&\phi _{2}&\cdots &\phi _{p-1}&\phi _{p}\\1&0&\cdots &0&0\\0&1&\cdots &0&0\\0&0&\ddots &0&0\\\vdots &\vdots &\cdots &\vdots &\vdots \\0&0&\cdots &1&0\end{array}}\right)=\left({\begin{array}{cc}{\begin{array}{cccc}\phi _{1}&\phi _{2}&\cdots &\phi _{p-1}\end{array}}&\phi _{p}\\I_{p-1}&0\end{array}}\right)$,

then the state space form is

$X_{t}=e_{1}^{'}E_{t},\;t\geq p$

${\boldsymbol {\boldsymbol {X}}}_{p}=G{\boldsymbol {\boldsymbol {X}}}_{p-1}^{'}+e_{1}\varepsilon _{p}where{\boldsymbol {\boldsymbol {X}}}_{p}^{'}=\left({\begin{array}{cccc}X_{p-1}&X_{p-2}&\cdots &X_{0}\end{array}}\right)$

${\text{E}}\left({\boldsymbol {\boldsymbol {X}}}_{p}\right)=0$ ${\text{Var}}\left({\boldsymbol {\boldsymbol {X}}}_{p}\right)=G{\text{Var}}\left({\boldsymbol {\boldsymbol {X}}}_{p-1}\right)G^{'}+{\text{Var}}\left(\varepsilon _{p}\right)e_{1}e_{1}^{'}$, if stationarity is imposed, then ${\text{Var}}\left({\boldsymbol {\boldsymbol {X}}}_{p}\right)={\text{Var}}\left({\boldsymbol {\boldsymbol {X}}}_{p-1}\right)=\Omega _{p}$, i.e.$\Omega _{p}=G\Omega _{p}G^{'}+\sigma ^{2}e_{1}e_{1}^{'}.{\text{vec}}\left(\Omega _{p}\right)=\left(G\otimes G\right){\text{vec}}\left(\Omega _{p}\right)+\sigma ^{2}{\text{vec}}\left(e_{1}e_{1}^{'}\right)=\sigma ^{2}\left(I-G\otimes G\right)^{-1}{\text{vec}}\left(e_{1}e_{1}^{'}\right).$

${\text{vec}}\left(ABC\right)=\left(C^{'}\otimes A\right){\text{vec}}\left(B\right).$ Jackzhp (talk) 19:25, 26 March 2011 (UTC)

OLS procedure

I feel that it is necessary to mention the reason why people don't apply the Ordinary least squares to estimate the coefficients. Jackzhp (talk) 19:25, 26 March 2011 (UTC)

AR(2) Spectrum

The page used to state that

For AR(2), the spectrum has a minimum ($\varphi _{2}>0$) or maximum ($\varphi _{2}<0$) if

$|\varphi _{1}(1-\varphi _{2})|<4|\varphi _{2}|.$

However, I am almost certain this is wrong. The critical points of the AR(2) spectrum occur when

$\varphi _{1}(1-\varphi _{2})\sin(\omega )+4\varphi _{2}\sin(\omega )\cos(\omega )=0$

Thus they occur at $\omega =2\pi k$ or at $\omega =\cos ^{-1}{\frac {\varphi _{1}(1-\varphi _{2})}{4\varphi _{2}}}$. I believe the person who posted the above made the mistake of dividing by sin (which is sometimes zero) and thus eliminating some of the potential peaks.

Inadequate graph caption

AR(0), AR(1), and AR(2) processes with white noise

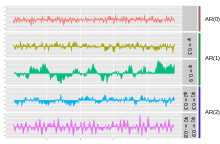
This graph caption in the section "Graphs of AR(p) processes" is inadequate. There are five subgraphs but the caption only explains three (presumably the top three??). The numbers by the right side of each subgraph are undefined. And from the original documentation, I can't even confirm that the caption is correct in referring to the top three subgraphs. Can someone figure this out and redo the caption? Thanks. Duoduoduo (talk) 15:31, 10 January 2013 (UTC)

AR(0), AR(1), and AR(2) processes with white noise

The graph makes sense in the context of the section where it is included. There is only one possible plot for AR(0) since there are no parameters. There are two plots for AR(1), one for a value of φ close to zero and another for φ just less than one. The last two plots are for AR(2). One plot is for where φ₁ and φ₂ have the same sign. The other plot is when the two parameters have different signs.

I agree the graph could use some more work to make it clearer. I will look into it.— Preceding unsigned comment added by Everettr2 (talk • contribs) 01:23, 13 January 2013 (UTC)

Thanks. I've clarified the caption based on your explanation. Duoduoduo (talk) 01:42, 13 January 2013 (UTC)

Edit to lede

@TheSeven: Please keep in mind WP:BRD -- you boldly made an edit, deleting a passage; I reverted your edit, then you are supposed to discuss on the talk page rather than edit war.

Your edit in the two-sentence long lede changes the second and last sentence from

The autoregressive model is one of a group of linear prediction formulas that attempt to predict an output of a system based on the previous outputs.

to

The autoregressive model is one of a group of linear prediction formulas.

thereby removing the passage

that attempt to predict an output of a system based on the previous outputs.

and your edit summary is

the wording suggested that they are only for prediction, which is untrue; also, prediction is already mentioned--keep intro clear and simple

(1) Not sure what you have in mind about other uses of AR. It seems to me that any others must be very minor or must actually be aspects of prediction. Can you be specific?

(2) I agree that predict should not be in there twice.

(3) The first sentence of the lede says that the AR model is a process, while the second sentence (both with and without your edit) says that it's a formula. That's awkward and needs to be fixed.

(4) Your deletion of the passage removes from the lede the most important thing there is to say about AR: based on the previous outputs. We can't possibly have a lede that doesn't even mention that.

I'm going to revert your edit as a violation of BRD and then rewrite the lede to take these things into account. Feel free to discuss here or to tweak my new version, or even to revert my new version to the original version, but please don't restore your version unless and until there arises a consensus on the talk page to do so. Duoduoduo (talk) 17:39, 30 January 2013 (UTC)

I really like the most-recent version. TheSeven (talk) 17:44, 31 January 2013 (UTC)

Wide sense stationarity for the AR(1) model : a contradiction ?

It is said that "the AR(1) model with $|\varphi _{1}|\geq 1$ are not stationary". If one defines an AR(1) process a stationnary process $\{X_{t}\}$ for which, given a white noise $\{\varepsilon _{t}\}$, the equation $X_{t}=\varphi _{1}X_{t-1}+\varepsilon _{t}$ is true, then clearly when $\varphi _{1}>1$ the process defined by $X_{t}=-\sum _{k=1}^{\infty }\varphi _{1}^{-k}\varepsilon _{t+k}$, where the infinite sum is a mean square limit ($L^{2}$ limit), is a stationary solution of the equation. This is a contradiction with the non existence of a stationary AR(1) process whenever $|\varphi _{1}|\geq 1$

Response: The will be stationary, but not causal: it relies on future shocks to compute the present value.

Doesn't make sense. The last equation says that X_t depends on future values of epsilon. That conflicts with the AR(1) under discussion. Clearly OR. Loraof (talk) 21:24, 3 July 2016 (UTC)

In other words, while the forward-looking "solution" does give an identity when plugged into the AR equation and hence is a solution in that narrow sense, it is not a solution of the process because the process includes the direction of time, going from past to future. Loraof (talk) 03:32, 4 July 2016 (UTC)

It is true that this interpretation is unphysical. However, this does not change anything about the fact that the model itself is stationary. Causality and stationarity are related, yet not identical. Nmdwolf (talk) 10:53, 21 December 2022 (UTC)

External links modified

Hello fellow Wikipedians,

I have just modified one external link on Autoregressive model. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:

• Added archive https://web.archive.org/web/20121021015413/http://www3.stat.sinica.edu.tw:80/statistica/oldpdf/A15n112.pdf to http://www3.stat.sinica.edu.tw/statistica/oldpdf/A15n112.pdf

When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).

This message was posted before February 2018. After February 2018, "External links modified" talk page sections are no longer generated or monitored by InternetArchiveBot. No special action is required regarding these talk page notices, other than regular verification using the archive tool instructions below. Editors have permission to delete these "External links modified" talk page sections if they want to de-clutter talk pages, but see the RfC before doing mass systematic removals. This message is updated dynamically through the template {{source check}} (last update: 5 June 2024).

• If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
• If you found an error with any archives or the URLs themselves, you can fix them with this tool.

Cheers.—InternetArchiveBot (Report bug) 07:55, 22 October 2016 (UTC)

Multiplicities in characteristic polynomial

In the first line of the section "Characteristic polynomial" there is currently a "citation needed" tag with reason given as "a_k not defined as seems wrong." I think the form

$\rho (\tau )=\sum _{k=1}^{p}a_{k}y_{k}^{-|\tau |}$

is correct provided all roots of the characteristic polynomial

$\phi (B)=1-\sum _{k=1}^{p}\varphi _{k}B^{k}$

have multiplicity 1. That being said, if some roots have multiplicity $>1$, then the formula may fail. Suppose $y_{j}$ for $j=1,2,...,l$ are distinct roots of the characteristic polynomial with multiplicies $\nu _{j}$. Then the general form of autocorrelation function is

$\rho (\tau )=\sum _{j=1}^{l}\sum _{r=0}^{\nu _{j}-1}a_{jr}|\tau |^{r}y_{j}^{-|\tau |}$

Below I will give a proof for this. In applications it is probably okay to assume multiplicity = 1 as higher values are unlikely to occur, but I think it is probably worth to clarify that such assumptions are being made. Please let me know what you think.

Proof: By the autocorrelation version of the Yule-Walker equation, we have

$\rho (\tau )=\sum _{k=1}^{p}\varphi _{k}\rho (\tau -k)$

for all $\tau \geq 1$. This is a degree-$p$ homogenous linear difference equation, and we have $p-1$ boundary conditions

$\rho (0)=1$

$\rho (-1)=\rho (1)$

$...$

$\rho (-p+1)=\rho (p-1)$

If $\phi (B)$ has roots $y_{j}$ with multiplicies $\nu _{j}$, where $j=1,2,...,l$, then it is straightforward to verify that a basis for the general solution is $\tau ^{r}y_{j}^{-\tau }$, for $j=1,2,...,l$ and $r=0,1,...,\nu _{j}-1$. Thus

$\rho (\tau )=\sum _{j=1}^{l}\sum _{r=0}^{\nu _{j}-1}a_{jr}\tau ^{r}y_{j}^{-\tau }$

for all $\tau \geq -p+1$. The coefficients $a_{jr}$ are determined by requiring that the boundary conditions be satisfied. Finally, by the symmetry of $\rho (\tau )$, we get the desired expression

$\rho (\tau )=\sum _{j=1}^{l}\sum _{r=0}^{\nu _{j}-1}a_{jr}|\tau |^{r}y_{j}^{-|\tau |}$

Zxiong (talk) 07:56, 6 December 2018 (UTC)

I think you are correct, but I don't know a printed reference for this. Joanico (talk) 16:37, 4 July 2022 (UTC)