Small retrosnub icosicosidodecahedron

Small retrosnub icosicosidodecahedron
Type	Uniform star polyhedron
Elements	F = 112, E = 180 V = 60 (χ = −8)
Faces by sides	(40+60){3}+12{5/2}
Coxeter diagram
Wythoff symbol	| 3/2 3/2 5/2
Symmetry group	Ih, [5,3], *532
Index references	U72, C91, W118
Dual polyhedron	Small hexagrammic hexecontahedron
Vertex figure	(35.5/3)/2
Bowers acronym	Sirsid

3D model of a small retrosnub icosicosidodecahedron

In geometry, the small retrosnub icosicosidodecahedron (also known as a retrosnub disicosidodecahedron, small inverted retrosnub icosicosidodecahedron, or retroholosnub icosahedron) is a nonconvex uniform polyhedron, indexed as U₇₂. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. It is given a Schläfli symbol sr{⁵/₃,³/₂}.

The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries.

George Olshevsky nicknamed it the yog-sothoth (after the Cthulhu Mythos deity).

Convex hull

Its convex hull is a nonuniform truncated dodecahedron.

Truncated dodecahedron

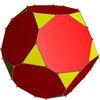Convex hull

Small retrosnub icosicosidodecahedron

Cartesian coordinates

Let $\xi =-{\frac {3}{2}}-{\frac {1}{2}}{\sqrt {1+4\phi }}\approx -2.866760399173862$ be the smallest (most negative) zero of the polynomial $P=x^{2}+3x+\phi ^{-2}$, where $\phi$ is the golden ratio. Let the point $p$ be given by

$p={\begin{pmatrix}\phi ^{-1}\xi +\phi ^{-3}\\\xi \\\phi ^{-2}\xi +\phi ^{-2}\end{pmatrix}}$.

Let the matrix $M$ be given by

$M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}$.

$M$ is the rotation around the axis $(1,0,\phi )$ by an angle of $2\pi /5$, counterclockwise. Let the linear transformations $T_{0},\ldots ,T_{11}$ be the transformations which send a point $(x,y,z)$ to the even permutations of $(\pm x,\pm y,\pm z)$ with an even number of minus signs. The transformations $T_{i}$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations $T_{i}M^{j}$ $(i=0,\ldots ,11$, $j=0,\ldots ,4)$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points $T_{i}M^{j}p$ are the vertices of a small snub icosicosidodecahedron. The edge length equals $-2\xi$, the circumradius equals ${\sqrt {-4\xi -\phi ^{-2}}}$, and the midradius equals ${\sqrt {-\xi }}$.

For a small snub icosicosidodecahedron whose edge length is 1, the circumradius is

$R={\frac {1}{2}}{\sqrt {\frac {\xi -1}{\xi }}}\approx 0.5806948001339209$

Its midradius is

$r={\frac {1}{2}}{\sqrt {\frac {-1}{\xi }}}\approx 0.2953073837589815$

The other zero of $P$ plays a similar role in the description of the small snub icosicosidodecahedron.

See also

• List of uniform polyhedra
• Small snub icosicosidodecahedron

External links

• Weisstein, Eric W. "Small retrosnub icosicosidodecahedron". MathWorld.
• Klitzing, Richard. "3D star small retrosnub icosicosidodecahedron".