Jump to content

Repetitive tuning

Add links
From Wikipedia, the free encyclopedia
Major-thirds tuning repeats itself (at a higher octave) after three strings. Thus, chords can be shifted vertically on the same frets.
The C major chord and its first and second inversions. In the first inversion, the C note has been raised 3 strings on the same fret. In the second inversion, both the C note and the E note have been raised 3 strings on the same fret.
Chords are inverted by shifting notes by three strings on the same fret in major-thirds tuning.[1]

Repetitive tunings are a type of alternative tunings for the guitar. A repetitive tuning begins with a list of notes that is duplicated, either at unison or at higher octaves.

Among regular tunings, there are four repetitive-tunings (besides trivially repetitive tunings such as C-C-C-C-C-C); this article discusses three minor-thirds tuning, major-thirds tuning, and augmented-fourths tuning (but not major seconds tuning, which is not repetitive on six strings). Among open tunings, there are repetitive versions of open C tuning and open G tuning, which have been associated with the English and Russian guitars, respectively.

Repetition eases the learning of fretboard and chords and eases improvisation. For example, in major-thirds tuning, chords are raised an octave by shifting fingers by three strings on the same frets.[2]

Repetitive tunings are listed after their number of open pitches. For example, the repetitive open-C tuning C-E-G-C-E-G has three open-pitches, each of which is associated with repeated notes {(C,C), (E,E), (G,G)}.

One

[edit]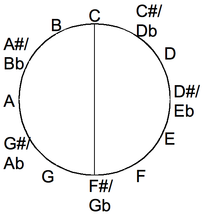
Every augmented-fourths (tritone) tunings repeats its two notes three times.

The trivial tuning repeats the same note every string. It is also called a unison regular tuning.

C-C-C-C-C-C.[3]

Other trivial-tunings repeat their single notes on a higher octave (or on higher octaves), for example,

C-C-c-c-c'-c'.

Two

[edit]

The following tunings repeat their notes on a higher octave after two strings:

Any note fingered on one string can be fingered on two other strings. Thus chords can be fingered in many ways in augmented-fourths tuning. It is also a regular tuning in which the interval between its strings is a tritone (augmented fourth).[4]

There are other tunings for the cittern.[6]

  • Alternating fourths and fifths tuning, such as A1-D2-A2-D3-A3-D4. (ADADAD)

This kind of tuning can also be called modal D or open D5 as it contains a D chord without a third. It is also used on other instruments, e.g. fiddle, mandolin and the Irish bouzouki.

Three

[edit]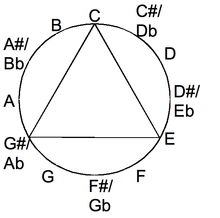
Every major-thirds tuning repeats its three notes twice.
For the Russian guitar, the open strings form a G-major chord, which is twice repeated

The following tunings repeat their notes after three strings:

D♯-G-B-D♯-G-B-D♯,[7]

Chord inversion is especially simple in major-thirds tuning. Chords are inverted simply by raising one or two notes three strings. The raised notes are played with the same finger as the original notes. The major-thirds tuning is also a regular tuning having a major third interval between strings.[1][2]

Four

[edit]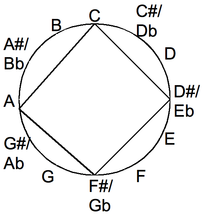
Minor-thirds tunings repeat its four notes after four strings (twice on an eight-string guitar).

In each minor-thirds tuning, every interval between successive strings is a minor third. It repeats its open-notes after four strings. Doubled notes have different sounds because of differing "string widths, tensions and tunings, and [they] reinforce each other, like the doubled strings of a twelve string guitar add chorusing and depth," according to William Sethares.[14]

In the minor-thirds tuning beginning with C,

C-D♯-F♯-a-c-d♯

the open strings contain the notes (c, d♯, f♯) of the diminished C chord. The minor-thirds tuning is also a regular tuning, which has a minor third interval between consecutive strings.[14]

See also

[edit]

Notes

[edit]
  1. ^ a b Kirkeby (2012, "Fretmaps, major chords: Major Triads"): Kirkeby, Ole (1 March 2012). "Major thirds tuning". m3guitar.com. cited by Sethares (2011) and Griewank (2010, p. 1). Retrieved 10 June 2012.
  2. ^ a b Griewank (2010, p. 10)
  3. ^ Sethares (2001, "Regular tunings", p. 53; and "The augmented fourths tuning" 60):

    Sethares, Bill (2001). "Regular tunings". Alternate tuning guide (PDF). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. pp. 52–67. Retrieved 9 September 2012.
  4. ^ Sethares (2001, "The augmented fourth tuning", p. 60)
  5. ^ Sethares (2001i, "Instrumental tunings: Cittern tuning two, p. 42)
  6. ^ Sethares (2001i, pp. 34 and 41–42)

    Sethares, Bill (2001i). "Instrumental tunings". Alternate tuning guide (PDF). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. pp. 34–51. Retrieved 12 September 2012.
  7. ^ Sethares (2001, "The major third tuning", pp. 56–57)
  8. ^ Ophee, Matanya (ed.). 19th Century etudes for the Russian 7-string guitar in G Op. The Russian Collection. Vol. 9. Editions Orphee. PR.494028230.
  9. ^ Ophee, Matanya (ed.). Selected Concert Works for the Russian 7-String Guitar in G open tuning. The Russian Collection. Vol. 10 ("X"). Editions Orphee. PR.494028240.
  10. ^ Smith, Gerald Stanton (1984). Songs to seven strings: Russian guitar poetry and Soviet "mass song". Soviet history, politics, society, and thought. Indiana University Press. pp. 1–271. ISBN 978-0-253-35391-7.
  11. ^ Timofeyev, Oleg V. (1999). The golden age of the Russian guitar: Repertoire, performance practice, and social function of the Russian seven-string guitar music, 1800-1850. Duke University, Department of Music. pp. 1–584. University Microfilms (UMI), Ann Arbor, Michigan, number 9928880.
  12. ^ Sethares (2001o, The open C tuning, p. 18):

    Sethares, Bill (2001o). "Open tunings". Alternate tuning guide (PDF). Madison, Wisconsin: University of Wisconsin; Department of Electrical Engineering. pp. 16–33. Retrieved 9 September 2012.
  13. ^ Hannu Annala; Heiki Mätlik (2007). "Composers for other plucked instruments: Rudolf Straube (1717-1785)". Handbook of Guitar and Lute Composers. Translated by Katarina Backman. Mel Bay. p. 30. ISBN 978-0-7866-5844-2.
  14. ^ a b Sethares (2001, "The minor third tuning", p. 54)

References

[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Repetitive_tuning&oldid=1177632533"