Portal:Mathematics/Selected picture/26
Appearance
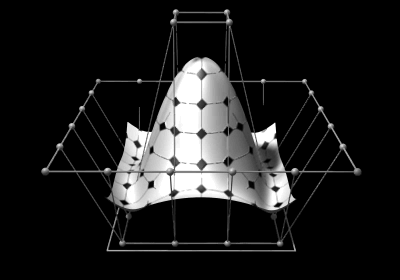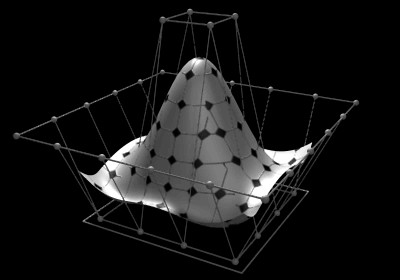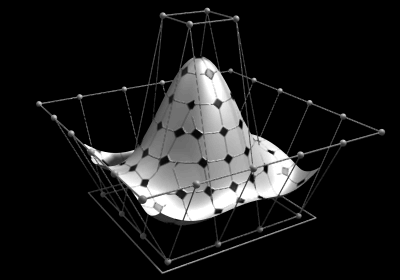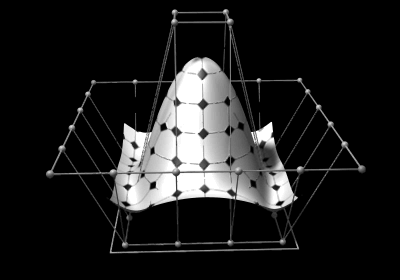
Non-uniform rational B-splines (NURBS) are commonly used in computer graphics for generating and representing curves and surfaces for both analytic shapes (described by mathematical formulas) and modeled shapes. Here the shape of the surface is determined by control points, shown as small spheres surrounding the surface itself. The square at the bottom sets the maximum width and length of the surface. Based on early work by Pierre Bézier and Paul de Casteljau, NURBS are generalizations of both B-splines (basis splines) and Bézier curves and surfaces. Unlike simple Bézier curves and surfaces, which are non-rational, NURBS can represent exactly certain analytic shapes such as conic sections and spherical sections. They are widely used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE), although T-splines and subdivision surfaces may be more suitable for more complex organic shapes.
