Portal:Mathematics/Selected picture/10
Appearance
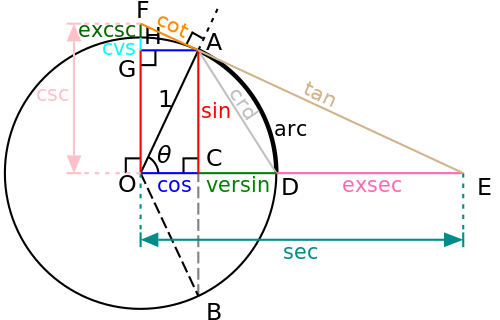
Credit: Steven G. Johnson (original version)
This is a graphical construction of the various trigonometric functions from a unit circle centered at the origin, O, and two points, A and D, on the circle separated by a central angle θ. The triangle AOC has side lengths cos θ (OC, the side adjacent to the angle θ) and sin θ (AC, the side opposite the angle), and a hypotenuse of length 1 (because the circle has unit radius). When the tangent line AE to the circle at point A is drawn to meet the extension of OD beyond the limits of the circle, the triangle formed, AOE, contains sides of length tan θ (AE) and sec θ (OE). When the tangent line is extended in the other direction to meet the line OF drawn perpendicular to OC, the triangle formed, AOF, has sides of length cot θ (AF) and csc θ (OF). In addition to these common trigonometric functions, the diagram also includes some functions that have fallen into disuse: the chord (AD), versine (CD), exsecant (DE), coversine (GH), and excosecant (FH). First used in the early Middle Ages by Indian and Islamic mathematicians to solve simple geometrical problems (e.g., solving triangles), the trigonometric functions today are used in sophisticated two- and three-dimensional computer modeling (especially when rotating modeled objects), as well as in the study of sound and other mechanical waves, light (electromagnetic waves), and electrical networks.
