Portal:Mathematics/Selected article/31
Selected article 31
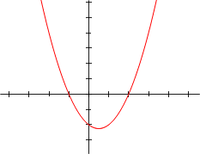 |
| The graph of a real-valued quadratic function of a real variable x, is a parabola. Image credit: Enoch Lau |
A quadratic equation is a polynomial equation of degree two. The general form is
where a ≠ 0 (if a = 0, then the equation becomes a linear equation). The letters a, b, and c are called coefficients: the quadratic coefficient a is the coefficient of x2, the linear coefficient b is the coefficient of x, and c is the constant coefficient, also called the free term.
Quadratic equations are known by that name because quadratus is Latin for "square"; in the leading term the variable is squared.
A quadratic equation has two (not necessarily distinct) solutions, which may be real or complex, given by the quadratic formula:
If the discriminant , then the quadratic equation has two distinct real solutions; if , the equation has two real solutions which are equal; if , the equation has two complex solutions.
These solutions are roots of the corresponding quadratic function
| View all selected articles |






