Pierre Hérigone
Pierre Hérigone (Latinized as Petrus Herigonius) (1580–1643) was a French mathematician and astronomer.
Of Basque origin, Hérigone taught in Paris for most of his life.
Works
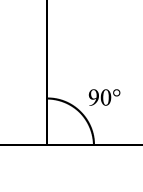
[edit]Only one work by Hérigone is known to exist:[1] Cursus mathematicus, nova, brevi, et clara methodo demonstratus, per notas reales et universales, citra usum cujuscunque idiomatis intellectu faciles (published in Paris in six volumes from 1634 to 1637; second edition 1644), a compendium of elementary mathematics written in French and Latin. The work introduced a system of mathematical and logical notation. It has been said that "Hérigone introduced so many new symbols in this six-volume work that some suggest that the introduction of these symbols, rather than an effective mathematics text, was his goal." Florian Cajori has written that the work contains "a full recognition of the importance of notation and an almost reckless eagerness to introduce an exhaustive set of symbols..."[2] Hérigone may have been the first to introduce the mathematical symbol to express an angle. He used both the symbol below and recorded the use of "<" as a symbol denoting "less than."
 |
He also introduced the upside-down "T" symbol (⊥) to express perpendicularity.
In regards to the notation for exponents, Herigone wrote a, a2, a3, etc. (though the numerals were not raised, however, as they are today).
Hérigone also created a number alphabet for remembering long numbers in which phonemes were assigned to different numbers, while the vowels were supplied by the memorizer: 1 (t, d), 2 (n), 3 (m), 4 (r), 5 (l), 6 (j, ch, sh), 7 (c, k, g), 8 (f, v, ph), 9 (p, b), 10 (z, s).[citation needed] (see article Herigone's mnemonic system).
In Hérigone's work, we find the earliest written examples of mathematical terms. Parallelipipedon, an archaic form of parallelepiped, appears in an English work dated 1570. Hérigone himself used the spelling parallelepipedum.
Hérigone and the camera obscura
[edit]In the Cursus mathematicus, Hérigone describes a camera obscura in the form of a goblet (Chapter 6, page 113). Hérigone did not depict his goblet, but Johann Zahn would illustrate the design in his Oculus Artificialis Teledioptricus Sive Telescopium (1685). Hérigone's goblet-camera obscura, more a novelty than anything else, was constructed in such a way that you could spy on others while taking a drink. The device's 45-degree angle mirror had a stylized opening for the lens. The goblet had a cup made of glass where images could be seen. The lid bore a magnifying lens at the top.[1] The lens and mirror of this dinner table device for spying was situated at the base of the goblet's stem and served to project a real-time image onto the ground glass screen in the cup of the goblet.
Committee work
[edit]Hérigone served on a number of scientific committees, including one set up to determine whether Jean-Baptiste Morin's scheme for determining longitude from the Moon's motion was practical. Members of this committee included Étienne Pascal and Claude Mydorge.
He died in Paris.
The crater Herigonius on the Moon is named after him.
Notes
[edit]- ^ Esteve, Ma Rosa Massa (November 2008). "Symbolic language in early modern mathematics: The Algebra of Pierre Hérigone (1580–1643)". Historia Mathematica. 35 (4): 285–301. doi:10.1016/j.hm.2008.05.003.
- ^ "Universal Language".
