Pearcey integral

A plot of the absolute value of the Pearcey integral as a function of its two parameters.

A photograph of a cusp caustic produced by illuminating a flat surface with a laser beam through a droplet of water.

In mathematics, the Pearcey integral is defined as

$\operatorname {Pe} (x,y)=\int _{-\infty }^{\infty }\exp(i(t^{4}+xt^{2}+yt))\,dt.$

The Pearcey integral is a class of canonical diffraction integrals, often used in wave propagation and optical diffraction problems The first numerical evaluation of this integral was performed by Trevor Pearcey using the quadrature formula.

Reflective caustic generated from a circle and parallel rays. On one side, each point is contained in three light rays; on the other side, each point is contained in one light ray.

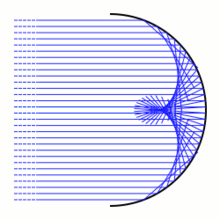
In optics, the Pearcey integral can be used to model diffraction effects at a cusp caustic, which corresponds to the boundary between two regions of geometric optics: on one side, each point is contained in three light rays; on the other side, each point is contained in one light ray.