The partition algebra is an associative algebra with a basis of set-partition diagrams and multiplication given by diagram concatenation .[ 1] Brauer algebra , the Temperley–Lieb algebra , or the group algebra of the symmetric group . Representations of the partition algebra are built from sets of diagrams and from representations of the symmetric group.
A partition of
2
k
{\displaystyle 2k}
1
,
1
¯
,
2
,
2
¯
,
…
,
k
,
k
¯
{\displaystyle 1,{\bar {1}},2,{\bar {2}},\dots ,k,{\bar {k}}}
{
1
¯
,
4
¯
,
5
¯
,
6
}
{\displaystyle \{{\bar {1}},{\bar {4}},{\bar {5}},6\}}
1
¯
−
4
¯
,
4
¯
−
5
¯
,
5
¯
−
6
{\displaystyle {\bar {1}}-{\bar {4}},{\bar {4}}-{\bar {5}},{\bar {5}}-6}
1
¯
−
6
,
4
¯
−
6
,
5
¯
−
6
,
1
¯
−
5
¯
{\displaystyle {\bar {1}}-6,{\bar {4}}-6,{\bar {5}}-6,{\bar {1}}-{\bar {5}}}
For
n
∈
C
{\displaystyle n\in \mathbb {C} }
k
∈
N
∗
{\displaystyle k\in \mathbb {N} ^{*}}
partition algebra
P
k
(
n
)
{\displaystyle P_{k}(n)}
C
{\displaystyle \mathbb {C} }
n
D
{\displaystyle n^{D}}
D
{\displaystyle D}
Generators and relations [ edit ] The partition algebra
P
k
(
n
)
{\displaystyle P_{k}(n)}
3
k
−
2
{\displaystyle 3k-2}
These generators obey relations that include[ 2]
s
i
2
=
1
,
s
i
s
i
+
1
s
i
=
s
i
+
1
s
i
s
i
+
1
,
p
i
2
=
n
p
i
,
b
i
2
=
b
i
,
p
i
b
i
p
i
=
p
i
{\displaystyle s_{i}^{2}=1\quad ,\quad s_{i}s_{i+1}s_{i}=s_{i+1}s_{i}s_{i+1}\quad ,\quad p_{i}^{2}=np_{i}\quad ,\quad b_{i}^{2}=b_{i}\quad ,\quad p_{i}b_{i}p_{i}=p_{i}}
Other elements that are useful for generating subalgebras include
In terms of the original generators, these elements are
e
i
=
b
i
p
i
p
i
+
1
b
i
,
l
i
=
s
i
p
i
,
r
i
=
p
i
s
i
{\displaystyle e_{i}=b_{i}p_{i}p_{i+1}b_{i}\quad ,\quad l_{i}=s_{i}p_{i}\quad ,\quad r_{i}=p_{i}s_{i}}
The partition algebra
P
k
(
n
)
{\displaystyle P_{k}(n)}
associative algebra . It has a multiplicative identity
The partition algebra
P
k
(
n
)
{\displaystyle P_{k}(n)}
semisimple for
n
∈
C
−
{
0
,
1
,
…
,
2
k
−
2
}
{\displaystyle n\in \mathbb {C} -\{0,1,\dots ,2k-2\}}
n
,
n
′
{\displaystyle n,n'}
P
k
(
n
)
{\displaystyle P_{k}(n)}
P
k
(
n
′
)
{\displaystyle P_{k}(n')}
[ 1]
The partition algebra is finite-dimensional, with
dim
P
k
(
n
)
=
B
2
k
{\displaystyle \dim P_{k}(n)=B_{2k}}
Bell number ).
Subalgebras of the partition algebra can be defined by the following properties:[ 3]
Whether they are planar i.e. whether lines may cross in diagrams.
Whether subsets are allowed to have any size
1
,
2
,
…
,
2
k
{\displaystyle 1,2,\dots ,2k}
1
,
2
{\displaystyle 1,2}
2
{\displaystyle 2}
Whether we allow top-top and bottom-bottom lines, or only top-bottom lines. In the latter case, the parameter
n
{\displaystyle n}
p
i
→
1
n
p
i
{\displaystyle p_{i}\to {\frac {1}{n}}p_{i}}
Combining these properties gives rise to 8 nontrivial subalgebras, in addition to the partition algebra itself:[ 1] [ 3]
Notation
Name
Generators
Dimension
Example
P
k
(
n
)
{\displaystyle P_{k}(n)}
Partition
s
i
,
p
i
,
b
i
{\displaystyle s_{i},p_{i},b_{i}}
B
2
k
{\displaystyle B_{2k}}
P
P
k
(
n
)
{\displaystyle PP_{k}(n)}
Planar partition
p
i
,
b
i
{\displaystyle p_{i},b_{i}}
1
2
k
+
1
(
4
k
2
k
)
{\displaystyle {\frac {1}{2k+1}}{\binom {4k}{2k}}}
R
B
k
(
n
)
{\displaystyle RB_{k}(n)}
Rook Brauer
s
i
,
e
i
,
p
i
{\displaystyle s_{i},e_{i},p_{i}}
∑
ℓ
=
0
k
(
2
k
2
ℓ
)
(
2
ℓ
−
1
)
!
!
{\displaystyle \sum _{\ell =0}^{k}{\binom {2k}{2\ell }}(2\ell -1)!!}
M
k
(
n
)
{\displaystyle M_{k}(n)}
Motzkin
e
i
,
l
i
,
r
i
{\displaystyle e_{i},l_{i},r_{i}}
∑
ℓ
=
0
k
1
ℓ
+
1
(
2
ℓ
ℓ
)
(
2
k
2
ℓ
)
{\displaystyle \sum _{\ell =0}^{k}{\frac {1}{\ell +1}}{\binom {2\ell }{\ell }}{\binom {2k}{2\ell }}}
B
k
(
n
)
{\displaystyle B_{k}(n)}
Brauer
s
i
,
e
i
{\displaystyle s_{i},e_{i}}
(
2
k
−
1
)
!
!
{\displaystyle (2k-1)!!}
T
L
k
(
n
)
{\displaystyle TL_{k}(n)}
Temperley–Lieb
e
i
{\displaystyle e_{i}}
1
k
+
1
(
2
k
k
)
{\displaystyle {\frac {1}{k+1}}{\binom {2k}{k}}}
R
k
{\displaystyle R_{k}}
Rook
s
i
,
p
i
{\displaystyle s_{i},p_{i}}
∑
ℓ
=
0
k
(
k
ℓ
)
2
ℓ
!
{\displaystyle \sum _{\ell =0}^{k}{\binom {k}{\ell }}^{2}\ell !}
P
R
k
{\displaystyle PR_{k}}
Planar rook
l
i
,
r
i
{\displaystyle l_{i},r_{i}}
(
2
k
k
)
{\displaystyle {\binom {2k}{k}}}
C
S
k
{\displaystyle \mathbb {C} S_{k}}
Symmetric group
s
i
{\displaystyle s_{i}}
k
!
{\displaystyle k!}
The symmetric group algebra
C
S
k
{\displaystyle \mathbb {C} S_{k}}
group ring of the symmetric group
S
k
{\displaystyle S_{k}}
C
{\displaystyle \mathbb {C} }
[ 4]
The listed subalgebras are semisimple for
n
∈
C
−
{
0
,
1
,
…
,
2
k
−
2
}
{\displaystyle n\in \mathbb {C} -\{0,1,\dots ,2k-2\}}
Inclusions of planar into non-planar algebras:
P
P
k
(
n
)
⊂
P
k
(
n
)
,
M
k
(
n
)
⊂
R
B
k
(
n
)
,
T
L
k
(
n
)
⊂
B
k
(
n
)
,
P
R
k
⊂
R
k
{\displaystyle PP_{k}(n)\subset P_{k}(n)\quad ,\quad M_{k}(n)\subset RB_{k}(n)\quad ,\quad TL_{k}(n)\subset B_{k}(n)\quad ,\quad PR_{k}\subset R_{k}}
Inclusions from constraints on subset size:
B
k
(
n
)
⊂
R
B
k
(
n
)
⊂
P
k
(
n
)
,
T
L
k
(
n
)
⊂
M
k
(
n
)
⊂
P
P
k
(
n
)
,
C
S
k
⊂
R
k
{\displaystyle B_{k}(n)\subset RB_{k}(n)\subset P_{k}(n)\quad ,\quad TL_{k}(n)\subset M_{k}(n)\subset PP_{k}(n)\quad ,\quad \mathbb {C} S_{k}\subset R_{k}}
Inclusions from allowing top-top and bottom-bottom lines:
R
k
⊂
R
B
k
(
n
)
,
P
R
k
⊂
M
k
(
n
)
,
C
S
k
⊂
B
k
(
n
)
{\displaystyle R_{k}\subset RB_{k}(n)\quad ,\quad PR_{k}\subset M_{k}(n)\quad ,\quad \mathbb {C} S_{k}\subset B_{k}(n)}
We have the isomorphism:
P
P
k
(
n
2
)
≅
T
L
2
k
(
n
)
,
{
p
i
↦
n
e
2
i
−
1
b
i
↦
1
n
e
2
i
{\displaystyle PP_{k}(n^{2})\cong TL_{2k}(n)\quad ,\quad \left\{{\begin{array}{l}p_{i}\mapsto ne_{2i-1}\\b_{i}\mapsto {\frac {1}{n}}e_{2i}\end{array}}\right.}
In addition to the eight subalgebras described above, other subalgebras have been defined:
The totally propagating partition subalgebra
prop
P
k
{\displaystyle {\text{prop}}P_{k}}
[ 5]
s
i
,
b
i
p
i
+
1
b
i
+
1
{\displaystyle s_{i},b_{i}p_{i+1}b_{i+1}}
[ 6]
The quasi-partition algebra
Q
P
k
(
n
)
{\displaystyle QP_{k}(n)}
s
i
,
b
i
,
e
i
{\displaystyle s_{i},b_{i},e_{i}}
1
+
∑
j
=
1
2
k
(
−
1
)
j
−
1
B
2
k
−
j
{\displaystyle 1+\sum _{j=1}^{2k}(-1)^{j-1}B_{2k-j}}
[ 7]
The uniform block permutation algebra
U
k
{\displaystyle U_{k}}
s
i
,
b
i
{\displaystyle s_{i},b_{i}}
[ 8] An algebra with a half-integer index
k
+
1
2
{\displaystyle k+{\frac {1}{2}}}
2
k
+
2
{\displaystyle 2k+2}
k
+
1
{\displaystyle k+1}
k
+
1
¯
{\displaystyle {\overline {k+1}}}
P
k
+
1
2
{\displaystyle P_{k+{\frac {1}{2}}}}
s
i
≤
k
−
1
,
b
i
≤
k
,
p
i
≤
k
{\displaystyle s_{i\leq k-1},b_{i\leq k},p_{i\leq k}}
P
k
⊂
P
k
+
1
2
⊂
P
k
+
1
{\displaystyle P_{k}\subset P_{k+{\frac {1}{2}}}\subset P_{k+1}}
dim
P
k
+
1
2
=
B
2
k
+
1
{\displaystyle \dim P_{k+{\frac {1}{2}}}=B_{2k+1}}
[ 2]
Periodic subalgebras are generated by diagrams that can be drawn on an annulus without line crossings. Such subalgebras include a translation element
u
=
{\displaystyle u=}
u
k
=
1
{\displaystyle u^{k}=1}
s
i
{\displaystyle s_{i}}
For an integer
0
≤
ℓ
≤
k
{\displaystyle 0\leq \ell \leq k}
D
ℓ
{\displaystyle D_{\ell }}
k
+
ℓ
{\displaystyle k+\ell }
1
,
2
,
…
,
k
{\displaystyle 1,2,\dots ,k}
1
¯
,
2
¯
,
…
,
ℓ
¯
{\displaystyle {\bar {1}},{\bar {2}},\dots ,{\bar {\ell }}}
k
=
12
,
ℓ
=
5
{\displaystyle k=12,\ell =5}
Partition diagrams act on
D
ℓ
{\displaystyle D_{\ell }}
S
ℓ
{\displaystyle S_{\ell }}
Specht module
V
λ
{\displaystyle V_{\lambda }}
S
ℓ
{\displaystyle S_{\ell }}
|
λ
|
=
ℓ
{\displaystyle |\lambda |=\ell }
P
k
(
n
)
{\displaystyle P_{k}(n)}
P
λ
=
C
D
|
λ
|
⊗
C
S
|
λ
|
V
λ
.
{\displaystyle {\mathcal {P}}_{\lambda }=\mathbb {C} D_{|\lambda |}\otimes _{\mathbb {C} S_{|\lambda |}}V_{\lambda }\ .}
The dimension of this representation is[ 1]
dim
P
λ
=
f
λ
∑
ℓ
=
|
λ
|
k
{
k
ℓ
}
(
ℓ
|
λ
|
)
,
{\displaystyle \dim {\mathcal {P}}_{\lambda }=f_{\lambda }\sum _{\ell =|\lambda |}^{k}\left\{{k \atop \ell }\right\}{\binom {\ell }{|\lambda |}}\ ,}
where
{
k
ℓ
}
{\displaystyle \left\{{k \atop \ell }\right\}}
Stirling number of the second kind ,
(
ℓ
|
λ
|
)
{\displaystyle {\binom {\ell }{|\lambda |}}}
binomial coefficient , and
f
λ
=
dim
S
λ
{\displaystyle f_{\lambda }=\dim S_{\lambda }}
hook length formula .
A basis of
P
λ
{\displaystyle {\mathcal {P}}_{\lambda }}
Young tableaux whose boxes are filled with the blocks of a set partition.[ 1]
Assuming that
P
k
(
n
)
{\displaystyle P_{k}(n)}
P
λ
{\displaystyle {\mathcal {P}}_{\lambda }}
Irrep
(
P
k
(
n
)
)
=
{
P
λ
}
0
≤
|
λ
|
≤
k
.
{\displaystyle {\text{Irrep}}\left(P_{k}(n)\right)=\left\{{\mathcal {P}}_{\lambda }\right\}_{0\leq |\lambda |\leq k}\ .}
Representations of subalgebras [ edit ] Representations of non-planar subalgebras have similar structures as representations of the partition algebra. For example, the Brauer-Specht modules of the Brauer algebra are built from Specht modules, and certain sets of partitions.
In the case of the planar subalgebras, planarity prevents nontrivial permutations, and Specht modules do not appear. For example, a standard module of the Temperley–Lieb algebra is parametrized by an integer
0
≤
ℓ
≤
k
{\displaystyle 0\leq \ell \leq k}
ℓ
≡
k
mod
2
{\displaystyle \ell \equiv k{\bmod {2}}}
The following table lists the irreducible representations of the partition algebra and eight subalgebras.[ 3]
Algebra
Parameter
Conditions
Dimension
P
k
(
n
)
{\displaystyle P_{k}(n)}
λ
{\displaystyle \lambda }
0
≤
|
λ
|
≤
k
{\displaystyle 0\leq |\lambda |\leq k}
f
λ
∑
ℓ
=
|
λ
|
k
{
k
ℓ
}
(
ℓ
|
λ
|
)
{\displaystyle f_{\lambda }\sum _{\ell =|\lambda |}^{k}\left\{{k \atop \ell }\right\}{\binom {\ell }{|\lambda |}}}
P
P
k
(
n
)
{\displaystyle PP_{k}(n)}
ℓ
{\displaystyle \ell }
0
≤
ℓ
≤
k
{\displaystyle 0\leq \ell \leq k}
(
2
k
k
+
ℓ
)
−
(
2
k
k
+
ℓ
+
1
)
{\displaystyle {\binom {2k}{k+\ell }}-{\binom {2k}{k+\ell +1}}}
R
B
k
(
n
)
{\displaystyle RB_{k}(n)}
λ
{\displaystyle \lambda }
0
≤
|
λ
|
≤
k
{\displaystyle 0\leq |\lambda |\leq k}
f
λ
(
k
|
λ
|
)
∑
m
=
0
⌊
k
−
|
λ
|
2
⌋
(
k
−
|
λ
|
2
m
)
(
2
m
−
1
)
!
!
{\displaystyle f_{\lambda }{\binom {k}{|\lambda |}}\sum _{m=0}^{\left\lfloor {\frac {k-|\lambda |}{2}}\right\rfloor }{\binom {k-|\lambda |}{2m}}(2m-1)!!}
M
k
(
n
)
{\displaystyle M_{k}(n)}
ℓ
{\displaystyle \ell }
0
≤
ℓ
≤
k
{\displaystyle 0\leq \ell \leq k}
∑
m
=
0
⌊
k
−
ℓ
2
⌋
(
k
ℓ
+
2
m
)
{
(
ℓ
+
2
m
m
)
−
(
ℓ
+
2
m
m
−
1
)
}
{\displaystyle \sum _{m=0}^{\left\lfloor {\frac {k-\ell }{2}}\right\rfloor }{\binom {k}{\ell +2m}}\left\{{\binom {\ell +2m}{m}}-{\binom {\ell +2m}{m-1}}\right\}}
B
k
(
n
)
{\displaystyle B_{k}(n)}
λ
{\displaystyle \lambda }
0
≤
|
λ
|
≤
k
|
λ
|
≡
k
mod
2
{\displaystyle {\begin{array}{c}0\leq |\lambda |\leq k\\|\lambda |\equiv k{\bmod {2}}\end{array}}}
f
λ
(
k
|
λ
|
)
(
k
−
|
λ
|
−
1
)
!
!
{\displaystyle f_{\lambda }{\binom {k}{|\lambda |}}(k-|\lambda |-1)!!}
T
L
k
(
n
)
{\displaystyle TL_{k}(n)}
ℓ
{\displaystyle \ell }
0
≤
ℓ
≤
k
ℓ
≡
k
mod
2
{\displaystyle {\begin{array}{c}0\leq \ell \leq k\\\ell \equiv k{\bmod {2}}\end{array}}}
(
k
k
+
ℓ
2
)
−
(
k
k
+
ℓ
+
2
2
)
{\displaystyle {\binom {k}{\frac {k+\ell }{2}}}-{\binom {k}{\frac {k+\ell +2}{2}}}}
R
k
{\displaystyle R_{k}}
λ
{\displaystyle \lambda }
0
≤
|
λ
|
≤
k
{\displaystyle 0\leq |\lambda |\leq k}
f
λ
(
k
|
λ
|
)
{\displaystyle f_{\lambda }{\binom {k}{|\lambda |}}}
P
R
k
{\displaystyle PR_{k}}
ℓ
{\displaystyle \ell }
0
≤
ℓ
≤
k
{\displaystyle 0\leq \ell \leq k}
(
k
ℓ
)
{\displaystyle {\binom {k}{\ell }}}
C
S
k
{\displaystyle \mathbb {C} S_{k}}
λ
{\displaystyle \lambda }
|
λ
|
=
k
{\displaystyle |\lambda |=k}
f
λ
{\displaystyle f_{\lambda }}
The irreducible representations of
prop
P
k
{\displaystyle {\text{prop}}P_{k}}
0
<
|
λ
|
≤
k
{\displaystyle 0<|\lambda |\leq k}
f
λ
{
k
|
λ
|
}
{\displaystyle f_{\lambda }\left\{{k \atop |\lambda |}\right\}}
[ 5]
Q
P
k
{\displaystyle QP_{k}}
0
≤
|
λ
|
≤
k
{\displaystyle 0\leq |\lambda |\leq k}
[ 7]
U
k
{\displaystyle U_{k}}
[ 8]
Assume
n
∈
N
∗
{\displaystyle n\in \mathbb {N} ^{*}}
V
{\displaystyle V}
n
{\displaystyle n}
v
1
,
…
,
v
n
{\displaystyle v_{1},\dots ,v_{n}}
P
k
(
n
)
{\displaystyle P_{k}(n)}
V
⊗
k
{\displaystyle V^{\otimes k}}
{
1
,
1
¯
,
2
,
2
¯
,
…
,
k
,
k
¯
}
=
⊔
h
E
h
{\displaystyle \{1,{\bar {1}},2,{\bar {2}},\dots ,k,{\bar {k}}\}=\sqcup _{h}E_{h}}
(
v
j
1
⊗
⋯
⊗
v
j
k
)
{\displaystyle (v_{j_{1}}\otimes \cdots \otimes v_{j_{k}})}
[ 2]
(
⊔
h
E
h
)
j
1
,
j
2
,
…
,
j
k
j
1
¯
,
j
2
¯
,
…
,
j
k
¯
=
1
r
,
s
∈
E
h
⟹
j
r
=
j
s
.
{\displaystyle \left(\sqcup _{h}E_{h}\right)_{j_{1},j_{2},\dots ,j_{k}}^{j_{\bar {1}},j_{\bar {2}},\dots ,j_{\bar {k}}}=\mathbf {1} _{r,s\in E_{h}\implies j_{r}=j_{s}}\ .}
This matrix element is one if all indices corresponding to any given partition subset coincide, and zero otherwise. For example, the action of a Temperley–Lieb generator is
e
i
(
v
j
1
⊗
⋯
⊗
v
j
i
⊗
v
j
i
+
1
⊗
⋯
⊗
v
j
k
)
=
δ
j
i
,
j
i
+
1
∑
j
=
1
n
v
j
1
⊗
⋯
⊗
v
j
⊗
v
j
⊗
⋯
⊗
v
j
k
.
{\displaystyle e_{i}\left(v_{j_{1}}\otimes \cdots \otimes v_{j_{i}}\otimes v_{j_{i+1}}\otimes \cdots \otimes v_{j_{k}}\right)=\delta _{j_{i},j_{i+1}}\sum _{j=1}^{n}v_{j_{1}}\otimes \cdots \otimes v_{j}\otimes v_{j}\otimes \cdots \otimes v_{j_{k}}\ .}
Duality between the partition algebra and the symmetric group [ edit ] Let
n
≥
2
k
{\displaystyle n\geq 2k}
V
{\displaystyle V}
natural permutation representation of the symmetric group
S
n
{\displaystyle S_{n}}
n
{\displaystyle n}
V
=
[
n
−
1
,
1
]
⊕
[
n
]
{\displaystyle V=[n-1,1]\oplus [n]}
Then the partition algebra
P
k
(
n
)
{\displaystyle P_{k}(n)}
centralizer of the action of
S
n
{\displaystyle S_{n}}
V
⊗
k
{\displaystyle V^{\otimes k}}
P
k
(
n
)
≅
End
S
n
(
V
⊗
k
)
.
{\displaystyle P_{k}(n)\cong {\text{End}}_{S_{n}}\left(V^{\otimes k}\right)\ .}
Moreover, as a bimodule over
P
k
(
n
)
×
S
n
{\displaystyle P_{k}(n)\times S_{n}}
[ 1]
V
⊗
k
=
⨁
0
≤
|
λ
|
≤
k
P
λ
⊗
V
[
n
−
|
λ
|
,
λ
]
,
{\displaystyle V^{\otimes k}=\bigoplus _{0\leq |\lambda |\leq k}{\mathcal {P}}_{\lambda }\otimes V_{[n-|\lambda |,\lambda ]}\ ,}
where
[
n
−
|
λ
|
,
λ
]
{\displaystyle [n-|\lambda |,\lambda ]}
n
{\displaystyle n}
λ
{\displaystyle \lambda }
V
[
n
−
|
λ
|
,
λ
]
{\displaystyle V_{[n-|\lambda |,\lambda ]}}
Specht module of
S
n
{\displaystyle S_{n}}
Dualities involving subalgebras [ edit ] The duality between the symmetric group and the partition algebra generalizes the original Schur-Weyl duality between the general linear group and the symmetric group. There are other generalizations. In the relevant tensor product spaces, we write
V
n
{\displaystyle V_{n}}
n
{\displaystyle n}
Tensor product space
Group or algebra
Dual algebra or group
Comments
(
V
n
−
1
⊕
V
1
)
⊗
k
{\displaystyle \left(V_{n-1}\oplus V_{1}\right)^{\otimes k}}
S
n
{\displaystyle S_{n}}
P
k
(
n
)
{\displaystyle P_{k}(n)}
The duality for the full partition algebra
(
V
n
−
2
⊕
V
1
⊕
V
1
)
⊗
k
{\displaystyle \left(V_{n-2}\oplus V_{1}\oplus V_{1}\right)^{\otimes k}}
S
n
−
1
{\displaystyle S_{n-1}}
P
k
+
1
2
(
n
)
{\displaystyle P_{k+{\frac {1}{2}}}(n)}
Case of a partition algebra with a half-integer index[ 2]
V
n
⊗
k
{\displaystyle V_{n}^{\otimes k}}
G
L
n
(
C
)
{\displaystyle GL_{n}(\mathbb {C} )}
S
k
{\displaystyle S_{k}}
The original Schur-Weyl duality
V
n
⊗
k
{\displaystyle V_{n}^{\otimes k}}
O
(
n
)
{\displaystyle O(n)}
B
k
(
n
)
{\displaystyle B_{k}(n)}
Duality between the orthogonal group and the Brauer algebra
(
V
n
⊕
V
1
)
⊗
k
{\displaystyle \left(V_{n}\oplus V_{1}\right)^{\otimes k}}
O
(
n
)
{\displaystyle O(n)}
R
B
k
(
n
+
1
)
{\displaystyle RB_{k}(n+1)}
Duality between the orthogonal group and the rook Brauer algebra[ 9]
V
n
⊗
k
{\displaystyle V_{n}^{\otimes k}}
R
n
{\displaystyle R_{n}}
prop
P
k
{\displaystyle {\text{prop}}P_{k}}
Duality between the rook algebra and the totally propagating partition algebra[ 10] [ 5]
V
2
⊗
k
{\displaystyle V_{2}^{\otimes k}}
g
l
(
1
|
1
)
{\displaystyle gl(1|1)}
P
R
k
−
1
{\displaystyle PR_{k-1}}
Duality between a Lie superalgebra and the planar rook algebra[ 11]
V
n
−
1
⊗
k
{\displaystyle V_{n-1}^{\otimes k}}
S
n
{\displaystyle S_{n}}
Q
P
k
(
n
)
{\displaystyle QP_{k}(n)}
Duality between the symmetric group and the quasi-partition algebra[ 7]
V
n
⊗
r
⊗
(
V
n
∗
)
⊗
s
{\displaystyle V_{n}^{\otimes r}\otimes \left(V_{n}^{*}\right)^{\otimes s}}
G
L
n
(
C
)
{\displaystyle GL_{n}(\mathbb {C} )}
B
r
,
s
(
n
)
{\displaystyle B_{r,s}(n)}
Duality involving the walled Brauer algebra .[ 12]
^ a b c d e f Halverson, Tom; Jacobson, Theodore N. (2020). "Set-partition tableaux and representations of diagram algebras" . Algebraic Combinatorics . 3 (2): 509–538. arXiv :1808.08118v2 doi :10.5802/alco.102 . ISSN 2589-5486 . S2CID 119167251 . ^ a b c d Halverson, Tom; Ram, Arun (2005). "Partition algebras" . European Journal of Combinatorics . 26 (6): 869–921. arXiv :math/0401314v2 doi :10.1016/j.ejc.2004.06.005 . S2CID 1168919 . ^ a b c Colmenarejo, Laura; Orellana, Rosa; Saliola, Franco; Schilling, Anne; Zabrocki, Mike (2020). "An insertion algorithm on multiset partitions with applications to diagram algebras" . Journal of Algebra . 557 : 97–128. arXiv :1905.02071v2 doi :10.1016/j.jalgebra.2020.04.010 . S2CID 146121089 . ^ Jacobsen, Jesper Lykke; Ribault, Sylvain; Saleur, Hubert (2022). "Spaces of states of the two-dimensional O(n) and Potts models". arXiv :2208.14298 ^ a b c Mishra, Ashish; Srivastava, Shraddha (2021). "Jucys–Murphy elements of partition algebras for the rook monoid" . International Journal of Algebra and Computation . 31 (5): 831–864. arXiv :1912.10737v3 doi :10.1142/S0218196721500399 . ISSN 0218-1967 . S2CID 209444954 . ^ Maltcev, Victor (2007-03-16). "On a new approach to the dual symmetric inverse monoid I*X ". arXiv :math/0703478v1 ^ a b c Daugherty, Zajj; Orellana, Rosa (2014). "The quasi-partition algebra" . Journal of Algebra . 404 : 124–151. arXiv :1212.2596v1 doi :10.1016/j.jalgebra.2013.11.028 . S2CID 117848394 . ^ a b Orellana, Rosa; Saliola, Franco; Schilling, Anne; Zabrocki, Mike (2021-12-27). "Plethysm and the algebra of uniform block permutations". arXiv :2112.13909v1 math.CO ]. ^ Halverson, Tom; delMas, Elise (2014-01-02). "Representations of the Rook-Brauer Algebra" . Communications in Algebra . 42 (1): 423–443. arXiv :1206.4576v2 doi :10.1080/00927872.2012.716120 . ISSN 0092-7872 . S2CID 38469372 . ^ Kudryavtseva, Ganna; Mazorchuk, Volodymyr (2008). "Schur–Weyl dualities for symmetric inverse semigroups" . Journal of Pure and Applied Algebra . 212 (8): 1987–1995. arXiv :math/0702864 doi :10.1016/j.jpaa.2007.12.004 . S2CID 13564450 . ^ Benkart, Georgia; Moon, Dongho (2013-05-28). "Planar Rook Algebras and Tensor Representations of 𝔤𝔩(1 | 1)" . Communications in Algebra . 41 (7): 2405–2416. arXiv :1201.2482v1 doi :10.1080/00927872.2012.658533 . ISSN 0092-7872 . S2CID 119125305 . ^ Cox, Anton; Visscher, De; Doty, Stephen; Martin, Paul (2007-09-06). "On the blocks of the walled Brauer algebra". arXiv :0709.0851v1 math.RT ].
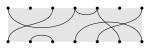




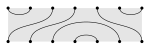



![]() such that . The translation element and its powers are the only combinations of that belong to periodic subalgebras.
such that . The translation element and its powers are the only combinations of that belong to periodic subalgebras.



























































































































![{\displaystyle V=[n-1,1]\oplus [n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad11f33d80ce125099614f6466b77cd9988342b)


![{\displaystyle V^{\otimes k}=\bigoplus _{0\leq |\lambda |\leq k}{\mathcal {P}}_{\lambda }\otimes V_{[n-|\lambda |,\lambda ]}\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8286ebe5ed8cd7d243b074a73df3e998032a7bf0)
![{\displaystyle [n-|\lambda |,\lambda ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a458d3cc8d26176fbf9ca0184431e5b4817ac5da)
![{\displaystyle V_{[n-|\lambda |,\lambda ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d39e85d160e312faad3538d945761d2394fde152)
















