Molecular demon

Fig.1 Schematic figure of Maxwell's demon thought experiment. The demon distinguishes fast-moving molecules from slow-moving ones and opens the small hatch selectively to let the fast-moving molecules pass from a A to B and the slow-moving molecules from B to A. Compartment B heats up whereas A cools down with respect to the average temperature although no work is done. It seems there is a contradiction with the second law of thermodynamics. But the ability to distinguish requires the gain of information, which is a form of energy; therefore. the system obeys the second law of thermodynamics inasmuch as information is first gained but then erased.

A molecular demon or biological molecular machine is a biological macromolecule that resembles and seems to have the same properties as Maxwell's demon. These macromolecules gather information in order to recognize their substrate or ligand within a myriad of other molecules floating in the intracellular or extracellular plasm. This molecular recognition represents an information gain which is equivalent to an energy gain or decrease in entropy. When the demon is reset i.e. when the ligand is released, the information is erased, energy is dissipated and entropy increases obeying the second law of thermodynamics. The difference between biological molecular demons and the thought experiment of Maxwell's demon is the latter's apparent violation of the second law.

Fig.2 The protein demon (blue) and the substrate or ligand (orange) go through a cycle in which the electromagnetic interaction (1' --> 2) between the two, following the induced fit, causes a conformational change upon which the substrate is released (2'). Hydrolysis of ATP brings the protein back to its original state

Cycle

The molecular demon switches mainly between two conformations. The first, or basic state, upon recognizing and binding the ligand or substrate following an induced fit, undergoes a change in conformation which leads to the second quasi-stable state: the protein-ligand complex. In order to reset the protein to its original, basic state, it needs ATP. When ATP is consumed or hydrolyzed, the ligand is released and the demon acquires again information reverting to its basic state. The cycle may start again.

Ratchet

The second law of thermodynamics is a statistical law. Hence, occasionally, single molecules may not obey the law. All molecules are subject to the molecular storm, i.e. the random movement of molecules in the cytoplasm and the extracellular fluid. Molecular demons or molecular machines either biological or artificially constructed are continuously pushed around by the random thermal motion in a direction that sometimes violates the law. When this happens and the gliding back of the macromolecule from the movement it had made or the conformational change it underwent to its original state can be prevented, as is the case with molecular demons, the molecule works as a ratchet; it is possible to observe for example the creation of a gradient of ions or other molecules across the cell membrane, the movement of motor proteins along filament proteins or also the accumulation of products deriving from an enzymatic reaction. Even some artificial molecular machines and experiments are capable of forming a ratchet apparently defying the second law of thermodynamics. All these molecular demons have to be reset to their original state consuming external energy that is subsequently dissipated as heat. This final step in which entropy increases is therefore irreversible. If the demons were reversible, no work would be done.

Artificial

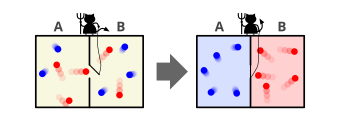
An example of artificial ratchets is the work by Serreli et al. (2007). Serreli et al. constructed a nanomachine, a rotaxane, that consists of a ring-shaped molecule, that moves along a tiny molecular axle between two different equal compartments, A and B. The normal, random movement of molecules sends the ring back and forth. Since the rings move freely, half of the rotaxanes have the ring on site B and the other half on site A. But the system used by Serreli et al. has a chemical gate on the rotaxane molecule and the axle contains two sticky parts, one at either side of the gate. This gate opens when the ring is close by. The sticky part in B is close to the gate and the rings pass more readily to A than from A to B. They obtained a deviation from equilibrium of 70:50 for A and B respectively, a bit like the demon of Maxwell. But this system works only when light is shone on it and thus needs external energy, just like molecular demons.

Energy and information

Landauer stated that information is physical. His principle sets fundamental thermodynamical constraints for classical and quantum information processing. Much effort has been dedicated to incorporating information into thermodynamics and measuring the entropic and energetic costs of manipulating information. Gaining information, decreases entropy which has an energy cost. This energy has to be collected from the environment. Landauer established equivalence of one bit of information with entropy which is represented by kT ln 2, where k is the Boltzmann constant and T is room temperature. This bound is called the Landauer's limit. Erasing energy increases entropy instead. Toyabe et al. (2010) were able to demonstrate experimentally that information can be converted in free energy. It is a quite elegant experiment that consists of a microscopic particle on a spiral-staircase-like potential. The step has a height corresponding to k_BT, where k_B is the Boltzmann constant and T is the temperature. The particle jumps between steps due to random thermal motions. Since the downward jumps following the gradient are more frequent than the upward ones, the particle falls down the stairs, on average. But when an upward jump is observed, a block is placed behind the particle to prevent it from falling, just like in a ratchet. This way it should climb the stairs. Information is gained by measuring the particle's location, which is equivalent to a gain in energy, i.e. a decrease in entropy. They used a generalized equation for the second law that contains a variable for information:

$\langle \Delta F-W\rangle \leq kTI$

ΔF is the free energy between states, W is the work done on the system, k is the Boltzmann constant, T is temperature, and I is the mutual information content obtained by measurements. The brackets indicate that the energy is an average. They could convert the equivalent of one bit information to 0.28 kT ln2 of energy or, in other words, they could exploit more than a quarter of the information’s energy content.

Cognitive demons

In his book Chance and Necessity, Jacques Monod described the functions of proteins and other molecules capable of recognizing with 'elective discrimination' a substrate or ligand or other molecule. In describing these molecules he introduced the term 'cognitive' functions, the same cognitive functions that Maxwell attributed to his demon. Werner Loewenstein goes further and names these molecules 'molecular demon' or 'demon' in short.

Naming the biological molecular machines in this way makes it easier to understand the similarities between these molecules and Maxwell's demon.

Because of this real discriminative if not 'cognitive' property, Jacques Monod attributed a teleonomic function to these biological complexes. Teleonomy implies the idea of an oriented, coherent and constructive activity. Proteins therefore must be considered essential molecular agents in the teleonomic performances of all living beings.

See also

• Molecular machine
• Protein–ligand complex
• Protein
• Ligand
• Maxwell's demon
• Jacques Monod
• Teleonomy