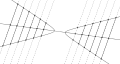Midpoint theorem (conics)
Appearance
In geometry, the midpoint theorem describes a property of parallel chords in a conic. It states that the midpoints of parallel chords in a conic are located on a common line.
The common line or line segment for the midpoints is called the diameter. For a circle, ellipse or hyperbola the diameter goes through its center. For a parabola the diameter is always perpendicular to its directrix and for a pair of intersecting lines (from a degenerate conic) the diameter goes through the point of intersection.
Gallery ( = eccentricity):
-
circle (=0)
-
ellipse (<1)
-
parabola (=1)
-
hyperbola (>1)
-
intersecting lines (=∞)
References
[edit]- David Alexander Brannan, Matthew F. Esplen, Jeremy J. Gray (1999) Geometry Cambridge University Press ISBN 9780521597876, pages 59–66
- Aleksander Simonic (November 2012) "On a Problem Concerning Two Conics", Crux Mathematicorum, volume 38(9): 372–377
- C. G. Gibson (2003) Elementary Euclidean Geometry: An Introduction. Cambridge University Press ISBN 9780521834483 pages 65–68
External links
[edit]- Locus of Midpoints of Parallel Chords of Central Conic passes through Center at the Proof Wiki
- midpoints of parallel chords in conics lie on a common line - interactive illustration