Jump to content

List of shapes with known packing constant

Add links
From Wikipedia, the free encyclopedia

The packing constant of a geometric body is the largest average density achieved by packing arrangements of congruent copies of the body. For most bodies the value of the packing constant is unknown.[1] The following is a list of bodies in Euclidean spaces whose packing constant is known.[1] Fejes Tóth proved that in the plane, a point symmetric body has a packing constant that is equal to its translative packing constant and its lattice packing constant.[2] Therefore, any such body for which the lattice packing constant was previously known, such as any ellipse, consequently has a known packing constant. In addition to these bodies, the packing constants of hyperspheres in 8 and 24 dimensions are almost exactly known.[3]

Image Description Dimension Packing constant Comments
Monohedral prototiles all 1 Shapes such that congruent copies can form a tiling of space
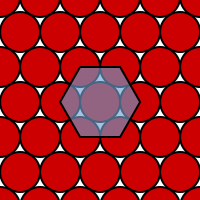Circle, Ellipse 2 π/√12 ≈ 0.906900 Proof attributed to Thue[4]
Regular pentagon 2 Thomas Hales and Wöden Kusner[5]
Smoothed octagon 2 Reinhardt[6]
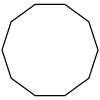All 2-fold symmetric convex polygons 2 Linear-time (in number of vertices) algorithm given by Mount and Ruth Silverman[7]
Sphere 3 π/√18 ≈ 0.7404805 See Kepler conjecture
Bi-infinite cylinder 3 π/√12 ≈ 0.906900 Bezdek and Kuperberg[8]
Half-infinite cylinder 3 π/√12 ≈ 0.906900 Wöden Kusner[9]
All shapes contained in a rhombic dodecahedron whose inscribed sphere is contained in the shape 3 Fraction of the volume of the rhombic dodecahedron filled by the shape Corollary of Kepler conjecture. Examples pictured: rhombicuboctahedron and rhombic enneacontahedron.
Hypersphere 8 See Hypersphere packing[10][11]
Hypersphere 24 See Hypersphere packing

References

[edit]
  1. ^ a b Bezdek, András; Kuperberg, Włodzimierz (2010). "Dense packing of space with various convex solids". arXiv:1008.2398v1 [math.MG].
  2. ^ Fejes Tóth, László (1950). "Some packing and covering theorems". Acta Sci. Math. Szeged. 12.
  3. ^ Cohn, Henry; Kumar, Abhinav (2009). "Optimality and uniqueness of the Leech lattice among lattices". Annals of Mathematics. 170 (3): 1003–1050. arXiv:math/0403263. doi:10.4007/annals.2009.170.1003. S2CID 10696627.
  4. ^ Chang, Hai-Chau; Wang, Lih-Chung (2010). "A Simple Proof of Thue's Theorem on Circle Packing". arXiv:1009.4322v1 [math.MG].
  5. ^ Hales, Thomas; Kusner, Wöden (2016). "Packings of regular pentagons in the plane". arXiv:1602.07220 [math.MG].
  6. ^ Reinhardt, Karl (1934). "Über die dichteste gitterförmige Lagerung kongruente Bereiche in der Ebene und eine besondere Art konvexer Kurven". Abh. Math. Sem. Univ. Hamburg. 10: 216–230. doi:10.1007/bf02940676. S2CID 120336230.
  7. ^ Mount, David M.; Silverman, Ruth (1990). "Packing and covering the plane with translates of a convex polygon". Journal of Algorithms. 11 (4): 564–580. doi:10.1016/0196-6774(90)90010-C.
  8. ^ Bezdek, András; Kuperberg, Włodzimierz (1990). "Maximum density space packing with congruent circular cylinders of infinite length". Mathematika. 37: 74–80. doi:10.1112/s0025579300012808.
  9. ^ Kusner, Wöden (2014). "Upper bounds on packing density for circular cylinders with high aspect ratio". Discrete & Computational Geometry. 51 (4): 964–978. arXiv:1309.6996. doi:10.1007/s00454-014-9593-6. S2CID 38234737.
  10. ^ Klarreich, Erica (March 30, 2016), "Sphere Packing Solved in Higher Dimensions", Quanta Magazine
  11. ^ Viazovska, Maryna (2016). "The sphere packing problem in dimension 8". Annals of Mathematics. 185 (3): 991–1015. arXiv:1603.04246. doi:10.4007/annals.2017.185.3.7. S2CID 119286185.
Retrieved from "https://en.wikipedia.org/w/index.php?title=List_of_shapes_with_known_packing_constant&oldid=1193146475"