List of electromagnetism equations
| Articles about |
| Electromagnetism |
|---|
 |
This article summarizes equations in the theory of electromagnetism.
Definitions
[edit]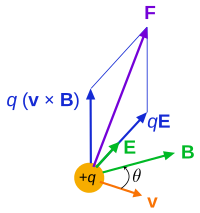
Here subscripts e and m are used to differ between electric and magnetic charges. The definitions for monopoles are of theoretical interest, although real magnetic dipoles can be described using pole strengths. There are two possible units for monopole strength, Wb (Weber) and A m (Ampere metre). Dimensional analysis shows that magnetic charges relate by qm(Wb) = μ0 qm(Am).
Initial quantities
[edit]| Quantity (common name/s) | (Common) symbol/s | SI units | Dimension |
|---|---|---|---|
| Electric charge | qe, q, Q | C = As | [I][T] |
| Monopole strength, magnetic charge | qm, g, p | Wb or Am | [L]2[M][T]−2 [I]−1 (Wb) [I][L] (Am) |
Electric quantities
[edit]
Contrary to the strong analogy between (classical) gravitation and electrostatics, there are no "centre of charge" or "centre of electrostatic attraction" analogues.[citation needed]
Electric transport
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Linear, surface, volumetric charge density | λe for Linear, σe for surface, ρe for volume. |
|
C m−n, n = 1, 2, 3 | [I][T][L]−n |
| Capacitance | C |
V = voltage, not volume. |
F = C V−1 | [I]2[T]4[L]−2[M]−1 |
| Electric current | I | A | [I] | |
| Electric current density | J | A m−2 | [I][L]−2 | |
| Displacement current density | Jd | A m−2 | [I][L]−2 | |
| Convection current density | Jc | A m−2 | [I][L]−2 |
Electric fields
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Electric field, field strength, flux density, potential gradient | E | N C−1 = V m−1 | [M][L][T]−3[I]−1 | |
| Electric flux | ΦE | N m2 C−1 | [M][L]3[T]−3[I]−1 | |
| Absolute permittivity; | ε | F m−1 | [I]2 [T]4 [M]−1 [L]−3 | |
| Electric dipole moment | p |
a = charge separation directed from -ve to +ve charge |
C m | [I][T][L] |
| Electric Polarization, polarization density | P | C m−2 | [I][T][L]−2 | |
| Electric displacement field, flux density | D | C m−2 | [I][T][L]−2 | |
| Electric displacement flux | ΦD | C | [I][T] | |
| Absolute electric potential, EM scalar potential relative to point
Theoretical: |
φ ,V | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Voltage, Electric potential difference | Δφ,ΔV | V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
Magnetic quantities
[edit]Magnetic transport
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Linear, surface, volumetric pole density | λm for Linear, σm for surface, ρm for volume. |
|
Wb m−n A m(−n + 1), |
[L]2[M][T]−2 [I]−1 (Wb) [I][L] (Am) |
| Monopole current | Im | Wb s−1 A m s−1 |
[L]2[M][T]−3 [I]−1 (Wb) [I][L][T]−1 (Am) | |
| Monopole current density | Jm | Wb s−1 m−2 A m−1 s−1 |
[M][T]−3 [I]−1 (Wb) [I][L]−1[T]−1 (Am) |
Magnetic fields
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Magnetic field, field strength, flux density, induction field | B | T = N A−1 m−1 = Wb m−2 | [M][T]−2[I]−1 | |
| Magnetic potential, EM vector potential | A | T m = N A−1 = Wb m3 | [M][L][T]−2[I]−1 | |
| Magnetic flux | ΦB | Wb = T m2 | [L]2[M][T]−2[I]−1 | |
| Magnetic permeability | V·s·A−1·m−1 = N·A−2 = T·m·A−1 = Wb·A−1·m−1 | [M][L][T]−2[I]−2 | ||
| Magnetic moment, magnetic dipole moment | m, μB, Π |
Two definitions are possible: using pole strengths, using currents: a = pole separation N is the number of turns of conductor |
A m2 | [I][L]2 |
| Magnetization | M | A m−1 | [I] [L]−1 | |
| Magnetic field intensity, (AKA field strength) | H | Two definitions are possible:
most common: using pole strengths,[1] |
A m−1 | [I] [L]−1 |
| Intensity of magnetization, magnetic polarization | I, J | T = N A−1 m−1 = Wb m−2 | [M][T]−2[I]−1 | |
| Self Inductance | L | Two equivalent definitions are possible:
|
H = Wb A−1 | [L]2 [M] [T]−2 [I]−2 |
| Mutual inductance | M | Again two equivalent definitions are possible:
1,2 subscripts refer to two conductors/inductors mutually inducing voltage/ linking magnetic flux through each other. They can be interchanged for the required conductor/inductor; |
H = Wb A−1 | [L]2 [M] [T]−2 [I]−2 |
| Gyromagnetic ratio (for charged particles in a magnetic field) | γ | Hz T−1 | [M]−1[T][I] |
Electric circuits
[edit]DC circuits, general definitions
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Terminal Voltage for | Vter | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Load Voltage for Circuit | Vload | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Internal resistance of power supply | Rint | Ω = V A−1 = J s C−2 | [M][L]2 [T]−3 [I]−2 | |
| Load resistance of circuit | Rext | Ω = V A−1 = J s C−2 | [M][L]2 [T]−3 [I]−2 | |
| Electromotive force (emf), voltage across entire circuit including power supply, external components and conductors | E | V = J C−1 | [M] [L]2 [T]−3 [I]−1 |
AC circuits
| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Resistive load voltage | VR | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Capacitive load voltage | VC | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Inductive load voltage | VL | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| Capacitive reactance | XC | Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 | |
| Inductive reactance | XL | Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 | |
| AC electrical impedance | Z |
|
Ω−1 m−1 | [I]2 [T]3 [M]−2 [L]−2 |
| Phase constant | δ, φ | dimensionless | dimensionless | |
| AC peak current | I0 | A | [I] | |
| AC root mean square current | Irms | A | [I] | |
| AC peak voltage | V0 | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| AC root mean square voltage | Vrms | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | |
| AC emf, root mean square | V = J C−1 | [M] [L]2 [T]−3 [I]−1 | ||
| AC average power | W = J s−1 | [M] [L]2 [T]−3 | ||
| Capacitive time constant | τC | s | [T] | |
| Inductive time constant | τL | s | [T] |
Magnetic circuits
[edit]| Quantity (common name/s) | (Common) symbol/s | Defining equation | SI units | Dimension |
|---|---|---|---|---|
| Magnetomotive force, mmf | F, |
N = number of turns of conductor |
A | [I] |
Electromagnetism
[edit]Electric fields
[edit]
General Classical Equations
| Physical situation | Equations |
|---|---|
| Electric potential gradient and field |
|
| Point charge | |
| At a point in a local array of point charges | |
| At a point due to a continuum of charge | |
| Electrostatic torque and potential energy due to non-uniform fields and dipole moments |
|
Magnetic fields and moments
[edit]
General classical equations
| Physical situation | Equations |
|---|---|
| Magnetic potential, EM vector potential | |
| Due to a magnetic moment |
|
| Magnetic moment due to a current distribution | |
| Magnetostatic torque and potential energy due to non-uniform fields and dipole moments |
|
Electric circuits and electronics
[edit]Below N = number of conductors or circuit components. Subscript net refers to the equivalent and resultant property value.
| Physical situation | Nomenclature | Series | Parallel |
|---|---|---|---|
| Resistors and conductors |
|
|
|
| Charge, capacitors, currents |
|
|
|
| Inductors |
|
|
| Circuit | DC Circuit equations | AC Circuit equations |
|---|---|---|
| RC circuits | Circuit equation
Capacitor charge Capacitor discharge |
|
| RL circuits | Circuit equation
Inductor current rise Inductor current fall |
|
| LC circuits | Circuit equation
|
Circuit equation
Circuit resonant frequency Circuit charge Circuit current Circuit electrical potential energy Circuit magnetic potential energy |
| RLC circuits | Circuit equation
|
Circuit equation
Circuit charge
|
See also
[edit]- Defining equation (physical chemistry)
- Fresnel equations
- List of equations in classical mechanics
- List of equations in fluid mechanics
- List of equations in gravitation
- List of equations in nuclear and particle physics
- List of equations in quantum mechanics
- List of equations in wave theory
- List of photonics equations
- List of relativistic equations
- SI electromagnetism units
- Table of thermodynamic equations
Footnotes
[edit]- ^ M. Mansfield; C. O'Sullivan (2011). Understanding Physics (2nd ed.). John Wiley & Sons. ISBN 978-0-470-74637-0.
Sources
[edit]- P.M. Whelan; M.J. Hodgeson (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
- G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2.
- A. Halpern (1988). 3000 Solved Problems in Physics, Schaum Series. Mc Graw Hill. ISBN 978-0-07-025734-4.
- R.G. Lerner; G.L. Trigg (2005). Encyclopaedia of Physics (2nd ed.). VHC Publishers, Hans Warlimont, Springer. pp. 12–13. ISBN 978-0-07-025734-4.
- C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (2nd ed.). McGraw Hill. ISBN 0-07-051400-3.
- P.A. Tipler; G. Mosca (2008). Physics for Scientists and Engineers: With Modern Physics (6th ed.). W.H. Freeman and Co. ISBN 978-1-4292-0265-7.
- L.N. Hand; J.D. Finch (2008). Analytical Mechanics. Cambridge University Press. ISBN 978-0-521-57572-0.
- T.B. Arkill; C.J. Millar (1974). Mechanics, Vibrations and Waves. John Murray. ISBN 0-7195-2882-8.
- H.J. Pain (1983). The Physics of Vibrations and Waves (3rd ed.). John Wiley & Sons. ISBN 0-471-90182-2.
- J.R. Forshaw; A.G. Smith (2009). Dynamics and Relativity. Wiley. ISBN 978-0-470-01460-8.
- G.A.G. Bennet (1974). Electricity and Modern Physics (2nd ed.). Edward Arnold (UK). ISBN 0-7131-2459-8.
- I.S. Grant; W.R. Phillips; Manchester Physics (2008). Electromagnetism (2nd ed.). John Wiley & Sons. ISBN 978-0-471-92712-9.
- D.J. Griffiths (2007). Introduction to Electrodynamics (3rd ed.). Pearson Education, Dorling Kindersley. ISBN 978-81-7758-293-2.
Further reading
[edit]- L.H. Greenberg (1978). Physics with Modern Applications. Holt-Saunders International W.B. Saunders and Co. ISBN 0-7216-4247-0.
- J.B. Marion; W.F. Hornyak (1984). Principles of Physics. Holt-Saunders International Saunders College. ISBN 4-8337-0195-2.
- A. Beiser (1987). Concepts of Modern Physics (4th ed.). McGraw-Hill (International). ISBN 0-07-100144-1.
- H.D. Young; R.A. Freedman (2008). University Physics – With Modern Physics (12th ed.). Addison-Wesley (Pearson International). ISBN 978-0-321-50130-1.
























































![{\displaystyle I_{\mathrm {rms} }={\sqrt {{\frac {1}{T}}\int _{0}^{T}\left[I\left(t\right)\right]^{2}\mathrm {d} t}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1def0a7f6e77cb4c21b955601a657047a645a97)

![{\displaystyle V_{\mathrm {rms} }={\sqrt {{\frac {1}{T}}\int _{0}^{T}\left[V\left(t\right)\right]^{2}\mathrm {d} t}}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a47cb2bc8518d427829d5d187367748f99a3dcf)
















































