Isolation forest

Isolation Forest is an algorithm for data anomaly detection using binary trees. It was developed by Fei Tony Liu in 2008. It has a linear time complexity and a low memory use, which works well for high-volume data. It is based on the assumption that because anomalies are few and different from other data, they can be isolated using few partitions. Like decision tree algorithms, it does not perform density estimation. Unlike decision tree algorithms, it uses only path length to output an anomaly score, and does not use leaf node statistics of class distribution or target value.

Isolation Forest is fast because it splits the data space, randomly selecting an attribute and split point. The anomaly score is inversely associated with the path-length because anomalies need fewer splits to be isolated, because they are few and different.

History

The Isolation Forest (iForest) algorithm was initially proposed by Fei Tony Liu, Kai Ming Ting and Zhi-Hua Zhou in 2008. In 2012 the same authors showed that iForest has linear time complexity, a small memory requirement, and is applicable to high-dimensional data. In 2010, an extension of the algorithm, SCiforest, was published to address clustered and axis-paralleled anomalies.

Isolation trees

An example of isolating a non-anomalous point in a 2D Gaussian distribution.

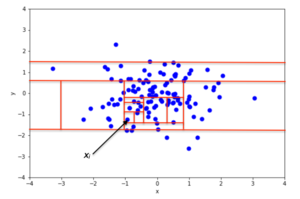
The premise of the Isolation Forest algorithm is that anomalous data points are easier to separate from the rest of the sample. In order to isolate a data point, the algorithm recursively generates partitions on the sample by randomly selecting an attribute and then randomly selecting a split value between the minimum and maximum values allowed for that attribute.

An example of isolating an anomalous point in a 2D Gaussian distribution.

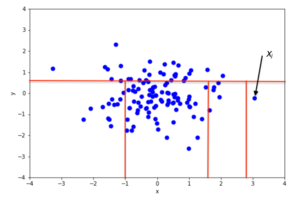
An example of random partitioning in a 2D dataset of normally distributed points is shown in the first figure for a non-anomalous point and in the second one for a point that is more likely to be an anomaly. It is apparent from the pictures how anomalies require fewer random partitions to be isolated, compared to normal points.

Recursive partitioning can be represented by a tree structure named Isolation Tree, while the number of partitions required to isolate a point can be interpreted as the length of the path, within the tree, to reach a terminating node starting from the root. For example, the path length of point $x_{i}$ in the first figure is greater than the path length of $x_{j}$ in the second figure.

Let $X=\{x_{1},\dots ,x_{n}\}$ be a set of d-dimensional points and $X'\subset X$. An Isolation Tree (iTree) is defined as a data structure with the following properties:

1. for each node $T$ in the Tree, $T$ is either an external-node with no child, or an internal-node with one “test” and exactly two child nodes ($T_{l}$ and $T_{r}$)
2. a test at node $T$ consists of an attribute $q$ and a split value $p$ such that the test $q<p$ determines the traversal of a data point to either $T_{l}$ or $T_{r}$.

In order to build an iTree, the algorithm recursively divides $X'$ by randomly selecting an attribute $q$ and a split value $p$, until either

1. the node has only one instance, or
2. all data at the node have the same values.

When the iTree is fully grown, each point in $X$ is isolated at one of the external nodes. Intuitively, the anomalous points are those (easier to isolate, hence) with the smaller path length in the tree, where the path length $h(x_{i})$ of point $x_{i}\in X$ is defined as the number of edges $x_{i}$ traverses from the root node to get to an external node.

A probabilistic explanation of iTree is provided in the original iForest paper.

Anomaly detection

Anomaly detection with Isolation Forest is done as follows:

1. Use the training dataset to build some number of iTrees
2. For each data point in the test set:
   1. Pass it through all the iTrees, counting the path length for each tree
   2. Assign an “anomaly score” to the instance
   3. Label the point as “anomaly” if its score is greater than a predefined threshold, which depends on the domain

Anomaly score

The algorithm for computing the anomaly score of a data point is based on the observation that the structure of iTrees is equivalent to that of Binary Search Trees (BST): a termination to an external node of the iTree corresponds to an unsuccessful search in the BST. Therefore the estimation of average $h(x)$ for external node terminations is the same as that of the unsuccessful searches in BST, that is

$c(m)={\begin{cases}2H(m-1)-{\frac {2(m-1)}{n}}&{\text{for }}m>2\\1&{\text{for }}m=2\\0&{\text{otherwise}}\end{cases}}$

where $n$ is the test set size, $m$ is the sample set size and $H$ is the harmonic number, which can be estimated by $H(i)=ln(i)+\gamma$, where $\gamma =0.5772156649$ is the Euler-Mascheroni constant.

Above, $c(m)$ is the average $h(x)$ given $m$, so we can use it to normalize $h(x)$ to get an estimate of the anomaly score for a given instance x:

$s(x,m)=2^{\frac {-E(h(x))}{c(m)}}$

where $E(h(x))$ is the average value of $h(x)$ from a collection of iTrees. For any data point $x$:

• if $s$ is close to $1$ then $x$ is very likely an anomaly
• if $s$ is smaller than $0.5$ then $x$ is likely normal
• if all points in the sample score around $0.5$, then likely they are all normal

Properties

• Sub-sampling: Because iForest does not need to isolate normal instances, it can often ignore most of the training set. Thus, it works very well when the sampling size is kept small, unlike most other methods, which benefit from a large sample size.
• Swamping: When normal instances are too close to anomalies, the number of partitions required to separate anomalies increases, a phenomenon known as swamping, which makes it more difficult for iForest to discriminate between anomalies and normal points. A main reason for swamping is the presence of too much data; so a possible solution is sub-sampling. Because iForest performs well under sub-sampling, reducing the number of points in the sample is also a good way to reduce the effect of swamping.
• Masking: When there are many anomalies, some of them can aggregate in a dense, large cluster, making it more difficult to separate the single anomalies and so to identify them. This phenomenon is called “masking”, and as with swamping, is more likely when the sample is big and can be alleviated through sub-sampling.
• High-dimensional data: A main limitation of standard, distance-based methods is their inefficiency in dealing with high dimensional data. The main reason is that in a high-dimensional space, every point is equally sparse, so using a distance-based measure of separation is ineffective. Unfortunately, high-dimensional data also affects the detection performance of iForest, but the performance can be vastly improved by using feature selection, like Kurtosis, to reduce the dimensionality of the sample.
• Normal instances only: iForest performs well even if the training set contains no anomalous points. This is because iForest describes data distributions such that long tree paths correspond to normal data points. Thus, the presence of anomalies is irrelevant to detection performance.

Open source implementations

Original implementation by Fei Tony Liu is Isolation Forest in R.

Other implementations (in alphabetical order):

• ELKI contains a Java implementation.
• Isolation Forest - A Spark/Scala implementation.
• Isolation Forest by H2O-3 - A Python implementation.
• Package solitude implementation in R.
• Python implementation with examples in scikit-learn.
• Spark iForest - A distributed Apache Spark implementation in Scala/Python.
• PyOD IForest - Another Python implementation in the popular Python Outlier Detection (PyOD) library.

Other variations of Isolation Forest algorithm implementations:

• Extended Isolation Forest – An implementation of Extended Isolation Forest.

• Extended Isolation Forest by H2O-3 - An implementation of Extended Isolation Forest.

• (Python, R, C/C++) Isolation Forest and variations - An implementation of Isolation Forest and its variations.

See also

• Anomaly detection