Inertial navigation system
This article's lead section may be too short to adequately summarize the key points. (September 2023) |


An inertial navigation system (INS; also inertial guidance system, inertial instrument) is a navigation device that uses motion sensors (accelerometers), rotation sensors (gyroscopes) and a computer to continuously calculate by dead reckoning the position, the orientation, and the velocity (direction and speed of movement) of a moving object without the need for external references.[1] Often the inertial sensors are supplemented by a barometric altimeter and sometimes by magnetic sensors (magnetometers) and/or speed measuring devices. INSs are used on mobile robots[2][3] and on vehicles such as ships, aircraft, submarines, guided missiles, and spacecraft.[4] Older INS systems generally used an inertial platform as their mounting point to the vehicle and the terms are sometimes considered synonymous.
Integrals in the time domain implicitly demand a stable and accurate clock for the quantification of elapsed time.
Design
[edit]Inertial navigation is a self-contained navigation technique in which measurements provided by accelerometers and gyroscopes are used to track the position and orientation of an object relative to a known starting point, orientation and velocity. Inertial measurement units (IMUs) typically contain three orthogonal rate-gyroscopes and three orthogonal accelerometers, measuring angular velocity and linear acceleration respectively. By processing signals from these devices it is possible to track the position and orientation of a device.
An inertial navigation system includes at least a computer and a platform or module containing accelerometers, gyroscopes, or other motion-sensing devices. The INS is initially provided with its position and velocity from another source (a human operator, a GPS satellite receiver, etc.) accompanied with the initial orientation and thereafter computes its own updated position and velocity by integrating information received from the motion sensors. The advantage of an INS is that it requires no external references in order to determine its position, orientation, or velocity once it has been initialized.
An INS can detect a change in its geographic position (a move east or north, for example), a change in its velocity (speed and direction of movement) and a change in its orientation (rotation about an axis). It does this by measuring the linear acceleration and angular velocity applied to the system. Since it requires no external reference (after initialization), it is immune to jamming and deception.
Gyroscopes measure the angular displacement of the sensor frame with respect to the inertial reference frame. By using the original orientation of the system in the inertial reference frame as the initial condition and integrating the angular displacement, the system's current orientation is known at all times. This can be thought of as the ability of a blindfolded passenger in a car to feel the car turn left and right or tilt up and down as the car ascends or descends hills. Based on this information alone, the passenger knows what direction the car is facing, but not how fast or slow it is moving, or whether it is sliding sideways.
Accelerometers measure the linear acceleration of the moving vehicle in the sensor or body frame, but in directions that can only be measured relative to the moving system (since the accelerometers are fixed to the system and rotate with the system, but are not aware of their own orientation). This can be thought of as the ability of a blindfolded passenger in a car to feel themself pressed back into their seat as the vehicle accelerates forward or pulled forward as it slows down; and feel themself pressed down into their seat as the vehicle accelerates up a hill or rise up out of their seat as the car passes over the crest of a hill and begins to descend. Based on this information alone, they know how the vehicle is accelerating relative to itself; that is, whether it is accelerating forward, backward, left, right, up (toward the car's ceiling), or down (toward the car's floor), measured relative to the car, but not the direction relative to the Earth, since they did not know what direction the car was facing relative to the Earth when they felt the accelerations.
However, by tracking both the current angular velocity of the system and the current linear acceleration of the system measured relative to the moving system, it is possible to determine the linear acceleration of the system in the inertial reference frame. Performing integration on the inertial accelerations (using the original velocity as the initial conditions) using the correct kinematic equations yields the inertial velocities of the system and integration again (using the original position as the initial condition) yields the inertial position. In our example, if the blindfolded passenger knew how the car was pointed and what its velocity was before they were blindfolded, and if they are able to keep track of both how the car has turned and how it has accelerated and decelerated since, then they can accurately know the current orientation, position, and velocity of the car at any time.
Uses
[edit]Inertial navigation is used in a wide range of applications including the navigation of aircraft, tactical and strategic missiles, spacecraft, submarines and ships. It is also embedded in some mobile phones for purposes of mobile phone location and tracking.[5][6] Recent advances in the construction of microelectromechanical systems (MEMS) have made it possible to manufacture small and light inertial navigation systems. These advances have widened the range of possible applications to include areas such as human and animal motion capture.
Inertial navigation systems are used in many different moving objects. However, their cost and complexity place constraints on the environments in which they are practical for use.
To support the use of inertial technology in the best way, already in 1965 a technical working group for Inertial Sensors had been established in Germany to bring together the users, the manufacturers and the researchers of inertial sensors. This working group has been continuously developed and today it is known as DGON ISA Inertial Sensors and Application Symposium, the leading conference for inertial technologies for more than 60 years. This Symposium DGON / IEEE ISA with about 200 international attendees is held annually in October in Germany. The publications of all DGON ISA conferences over the last more than 60 years are accessible.
Drift rate
[edit]All inertial navigation systems suffer from integration drift: small errors in the measurement of acceleration and angular velocity are integrated into progressively larger errors in velocity, which are compounded into still greater errors in position.[7][8] Since the new position is calculated from the previous calculated position and the measured acceleration and angular velocity, these errors accumulate roughly proportionally to the time since the initial position was input. Even the best accelerometers, with a standard error of 10 micro-g, would accumulate a 50-meter (164-ft) error within 17 minutes.[9] Therefore, the position must be periodically corrected by input from some other type of navigation system.
Accordingly, inertial navigation is usually used to supplement other navigation systems, providing a higher degree of accuracy than is possible with the use of any single system. For example, if, in terrestrial use, the inertially tracked velocity is intermittently updated to zero by stopping, the position will remain precise for a much longer time, a so-called zero velocity update. In aerospace particularly, other measurement systems are used to determine INS inaccuracies, e.g. the Honeywell LaseRefV inertial navigation systems uses GPS and air data computer outputs to maintain required navigation performance. The navigation error rises with the lower sensitivity of the sensors used. Currently, devices combining different sensors are being developed, e.g. attitude and heading reference system. Because the navigation error is mainly influenced by the numerical integration of angular rates and accelerations, the pressure reference system was developed to use one numerical integration of the angular rate measurements.
Estimation theory in general and Kalman filtering in particular,[10] provide a theoretical framework for combining information from various sensors. One of the most common alternative sensors is a satellite navigation radio such as GPS, which can be used for all kinds of vehicles with direct sky visibility. Indoor applications can use pedometers, distance measurement equipment, or other kinds of position sensors. By properly combining the information from an INS and other systems (GPS), the errors in position and velocity are stable. Furthermore, INS can be used as a short-term fallback while GPS signals are unavailable, for example when a vehicle passes through a tunnel.
In 2011, GPS jamming at the civilian level became a governmental concern.[11] The relative ease in ability to jam these systems has motivated the military to reduce navigation dependence on GPS technology.[12] Because inertial navigation sensors do not depend on radio signals unlike GPS, they cannot be jammed.[13] In 2012, the U.S. Army Research Laboratory reported a method to merge measurements from 10 pairs of MEMS gyroscope and accelerometers (plus occasional GPS), reducing the positional error by two thirds for a projectile. The algorithm can correct for systemic biases in individual sensors, using both GPS and a heuristic based on the gun-firing acceleration force. If one sensor consistently over or underestimates distance, the system can adjust the corrupted sensor's contributions to the final calculation.[14]
History
[edit]The examples and perspective in this section deal primarily with the United States and do not represent a worldwide view of the subject. (January 2015) |
Inertial navigation systems were originally developed for rockets. American rocketry pioneer Robert Goddard experimented with rudimentary gyroscopic systems. Goddard's systems were of great interest to contemporary German pioneers including Wernher von Braun. The systems entered more widespread use with the advent of spacecraft, guided missiles, and commercial airliners.
Early German World War II V2 guidance systems combined two gyroscopes and a lateral accelerometer with a simple analog computer to adjust the azimuth for the rocket in flight. Analog computer signals were used to drive four graphite rudders in the rocket exhaust for flight control. The GN&C (Guidance, Navigation, and Control) system for the V2 provided many innovations as an integrated platform with closed loop guidance. At the end of the war von Braun engineered the surrender of 500 of his top rocket scientists, along with plans and test vehicles, to the Americans. They arrived at Fort Bliss, Texas in 1945 under the provisions of Operation Paperclip and were subsequently moved to Huntsville, Alabama, in 1950[15] where they worked for U.S. Army rocket research programs.
In the early 1950s, the US government wanted to insulate itself against over-dependency on the German team for military applications, including the development of a fully domestic missile guidance program. The MIT Instrumentation Laboratory (later to become the Charles Stark Draper Laboratory, Inc.) was chosen by the Air Force Western Development Division to provide a self-contained guidance system backup to Convair in San Diego for the new Atlas intercontinental ballistic missile [16][17][18][19] (Construction and testing were completed by Arma Division of AmBosch Arma). The technical monitor for the MIT task was engineer Jim Fletcher, who later served as NASA Administrator. The Atlas guidance system was to be a combination of an on-board autonomous system and a ground-based tracking and command system. The self-contained system finally prevailed in ballistic missile applications for obvious reasons. In space exploration, a mixture of the two remains.
In the summer of 1952, Dr. Richard Battin and Dr. J. Halcombe "Hal" Laning, Jr., researched computational based solutions to guidance and undertook the initial analytical work on the Atlas inertial guidance in 1954. Other key figures at Convair were Charlie Bossart, the Chief Engineer, and Walter Schweidetzky, head of the guidance group. Schweidetzky had worked with von Braun at Peenemünde during World War II.
The initial Delta guidance system assessed the difference in position from a reference trajectory. A velocity to be gained (VGO) calculation is made to correct the current trajectory with the objective of driving VGO to zero. The mathematics of this approach were fundamentally valid, but dropped because of the challenges in accurate inertial guidance and analog computing power. The challenges faced by the Delta efforts were overcome by the Q system (see Q-guidance) of guidance. The Q system's revolution was to bind the challenges of missile guidance (and associated equations of motion) in the matrix Q. The Q matrix represents the partial derivatives of the velocity with respect to the position vector. A key feature of this approach allowed for the components of the vector cross product (v, xdv, /dt) to be used as the basic autopilot rate signals—a technique that became known as cross-product steering. The Q-system was presented at the first Technical Symposium on Ballistic Missiles held at the Ramo-Wooldridge Corporation in Los Angeles on 21 and 22 June 1956. The Q system was classified information through the 1960s. Derivations of this guidance are used for today's missiles.
Guidance in human spaceflight
[edit]
In February 1961 NASA awarded MIT a contract for preliminary design study of a guidance and navigation system for the Apollo program. MIT and the Delco Electronics Div. of General Motors Corp. were awarded the joint contract for design and production of the Apollo Guidance and Navigation systems for the Command Module and the Lunar Module. Delco produced the IMUs (Inertial Measurement Units) for these systems, Kollsman Instrument Corp. produced the Optical Systems, and the Apollo Guidance Computer was built by Raytheon under subcontract.[20][21]
For the Space Shuttle, open loop guidance was used to guide the Shuttle from lift-off until Solid Rocket Booster (SRB) separation. After SRB separation the primary Space Shuttle guidance is named PEG (Powered Explicit Guidance). PEG takes into account both the Q system and the predictor-corrector attributes of the original "Delta" System (PEG Guidance). Although many updates to the Shuttle's navigation system had taken place over the last 30 years (ex. GPS in the OI-22 build), the guidance core of the Shuttle GN&C system had evolved little. Within a crewed system, there is a human interface needed for the guidance system. As astronauts are the customer for the system, many new teams were formed that touch GN&C as it is a primary interface to "fly" the vehicle.
Early use in aircraft inertial guidance
[edit]One example of a popular INS for commercial aircraft was the Delco Carousel, which provided partial automation of navigation in the days before complete flight management systems became commonplace. The Carousel allowed pilots to enter 9 waypoints at a time and then guided the aircraft from one waypoint to the next using an INS to determine aircraft position and velocity. Boeing Corporation subcontracted the Delco Electronics Div. of General Motors to design and build the first production Carousel systems for the early models (-100, -200 and -300) of the 747 aircraft. The 747 utilized three Carousel systems operating in concert for reliability purposes. The Carousel system and derivatives thereof were subsequently adopted for use in many other commercial and military aircraft. The USAF C-141 was the first military aircraft to utilize the Carousel in a dual system configuration, followed by the C-5A which utilized the triple INS configuration, similar to the 747. The KC-135A fleet was fitted with a single Carousel IV-E system that could operate as a stand-alone INS or can be aided by the AN/APN-81 or AN/APN-218 Doppler radar. Some special-mission variants of the C-135 were fitted with dual Carousel IV-E INSs. ARINC Characteristic 704 defines the INS used in commercial air transport.
Details
[edit]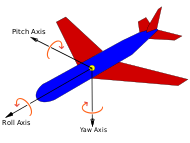

INSs contain Inertial Measurement Units (IMUs) which have angular and linear accelerometers (for changes in position); some IMUs include a gyroscopic element (for maintaining an absolute angular reference).
Angular accelerometers measure how the vehicle is rotating in space. Generally, there is at least one sensor for each of the three axes: pitch (nose up and down), yaw (nose left and right) and roll (clockwise or counter-clockwise from the cockpit).
Linear accelerometers measure non-gravitational accelerations[22] of the vehicle. Since it can move in three axes (up and down, left and right, forward and back), there is a linear accelerometer for each axis.
A computer continually calculates the vehicle's current position. First, for each of the six degrees of freedom (x,y,z and θx, θy and θz), it integrates over time the sensed acceleration, together with an estimate of gravity, to calculate the current velocity. Then it integrates the velocity to calculate the current position.
Inertial guidance is difficult without computers. The desire to use inertial guidance in the Minuteman missile and Project Apollo drove early attempts to miniaturize computers.
Inertial guidance systems are now usually combined with satellite navigation systems through a digital filtering system. The inertial system provides short term data, while the satellite system corrects accumulated errors of the inertial system.
An inertial guidance system that will operate near the surface of the earth must incorporate Schuler tuning so that its platform will continue pointing towards the center of the Earth as a vehicle moves from place to place.
Basic schemes
[edit]Gimballed gyrostabilized platforms
[edit]
Some systems place the linear accelerometers on a gimballed gyrostabilized platform. The gimbals are a set of three rings, each with a pair of bearings initially at right angles. They let the platform twist about any rotational axis (or, rather, they let the platform keep the same orientation while the vehicle rotates around it). There are two gyroscopes (usually) on the platform.
Two gyroscopes are used to cancel gyroscopic precession, the tendency of a gyroscope to twist at right angles to an input torque. By mounting a pair of gyroscopes (of the same rotational inertia and spinning at the same speed in opposite directions) at right angles the precessions are cancelled and the platform will resist twisting. [citation needed]
This system allows a vehicle's roll, pitch and yaw angles to be measured directly at the bearings of the gimbals. Relatively simple electronic circuits can be used to add up the linear accelerations, because the directions of the linear accelerometers do not change.
The big disadvantage of this scheme is that it uses many expensive precision mechanical parts. It also has moving parts that can wear out or jam and is vulnerable to gimbal lock. The primary guidance system of the Apollo spacecraft used a three-axis gyrostabilized platform, feeding data to the Apollo Guidance Computer. Maneuvers had to be carefully planned to avoid gimbal lock.
Fluid-suspended gyrostabilized platforms
[edit]Gimbal lock constrains maneuvering and it would be beneficial to eliminate the slip rings and bearings of the gimbals. Therefore, some systems use fluid bearings or a flotation chamber to mount a gyrostabilized platform. These systems can have very high precisions (e.g., Advanced Inertial Reference Sphere). Like all gyrostabilized platforms, this system runs well with relatively slow, low-power computers.
The fluid bearings are pads with holes through which pressurized inert gas (such as helium) or oil presses against the spherical shell of the platform. The fluid bearings are very slippery and the spherical platform can turn freely. There are usually four bearing pads, mounted in a tetrahedral arrangement to support the platform.
In premium systems, the angular sensors are usually specialized transformer coils made in a strip on a flexible printed circuit board. Several coil strips are mounted on great circles around the spherical shell of the gyrostabilized platform. Electronics outside the platform uses similar strip-shaped transformers to read the varying magnetic fields produced by the transformers wrapped around the spherical platform. Whenever a magnetic field changes shape, or moves, it will cut the wires of the coils on the external transformer strips. The cutting generates an electric current in the external strip-shaped coils and electronics can measure that current to derive angles.
Cheap systems sometimes use bar codes to sense orientations and use solar cells or a single transformer to power the platform. Some small missiles have powered the platform with light from a window or optic fibers to the motor. A research topic is to suspend the platform with pressure from exhaust gases. Data is returned to the outside world via the transformers, or sometimes LEDs communicating with external photodiodes.
Strapdown systems
[edit]Lightweight digital computers permit the system to eliminate the gimbals, creating strapdown systems, so called because their sensors are simply strapped to the vehicle. This reduces the cost, eliminates gimbal lock, removes the need for some calibrations and increases the reliability by eliminating some of the moving parts. Angular rate sensors called rate gyros measure the angular velocity of the vehicle.
A strapdown system needs a dynamic measurement range several hundred times that required by a gimballed system. That is, it must integrate the vehicle's attitude changes in pitch, roll and yaw, as well as gross movements. Gimballed systems could usually do well with update rates of 50–60 Hz. However, strapdown systems normally update about 2000 Hz. The higher rate is needed to let the navigation system integrate the angular rate into an attitude accurately.
The data updating algorithms (direction cosines or quaternions) involved are too complex to be accurately performed except by digital electronics. However, digital computers are now so inexpensive and fast that rate gyro systems can now be practically used and mass-produced. The Apollo lunar module used a strapdown system in its backup Abort Guidance System (AGS).
Strapdown systems are nowadays commonly used in commercial and military applications (aircraft, ships, ROVs, missiles, etc.). State-of-the-art strapdown systems are based upon ring laser gyroscopes, fibre optic gyrocopes or hemispherical resonator gyroscopes. They are using digital electronics and advanced digital filtering techniques such as Kalman filter.
Motion-based alignment
[edit]The orientation of a gyroscope system can sometimes also be inferred simply from its position history (e.g., GPS). This is, in particular, the case with planes and cars, where the velocity vector usually implies the orientation of the vehicle body.
For example, Honeywell's Align in Motion[23] is an initialization process where the initialization occurs while the aircraft is moving, in the air or on the ground. This is accomplished using GPS and an inertial reasonableness test, thereby allowing commercial data integrity requirements to be met. This process has been FAA certified to recover pure INS performance equivalent to stationary alignment procedures for civilian flight times up to 18 hours. It avoids the need for gyroscope batteries on aircraft.
Vibrating gyros
[edit]Less-expensive navigation systems, intended for use in automobiles, may use a vibrating structure gyroscope to detect changes in heading and the odometer pickup to measure distance covered along the vehicle's track. This type of system is much less accurate than a higher-end INS, but it is adequate for the typical automobile application where GPS is the primary navigation system and dead reckoning is only needed to fill gaps in GPS coverage when buildings or terrain block the satellite signals.
Hemispherical resonator gyros
[edit]If a standing wave is induced in a hemispheric resonant structure and then the resonant structure is rotated, the spherical harmonic standing wave rotates through an angle different from the quartz resonator structure due to the Coriolis force. The movement of the outer case with respect to the standing wave pattern is proportional to the total rotation angle and can be sensed by appropriate electronics. The system resonators are machined from fused quartz due to its excellent mechanical properties. The electrodes that drive and sense the standing waves are deposited directly onto separate quartz structures that surround the resonator. These gyros can operate in either a whole angle mode (which gives them nearly unlimited rate capability) or a force rebalance mode that holds the standing wave in a fixed orientation with respect to the gyro housing (which gives them much better accuracy).
This system has almost no moving parts and is very accurate. However it is still relatively expensive due to the cost of the precision ground and polished hollow quartz hemispheres. Northrop Grumman currently manufactures IMUs (inertial measurement units) for spacecraft that use HRGs. These IMUs have demonstrated extremely high reliability since their initial use in 1996.[24] Safran manufactures large numbers of HRG based inertial navigation systems dedicated to a wide range of applications.[25]
Quartz rate sensors
[edit]This section needs to be updated. (October 2018) |

These products include "tuning fork gyros". Here, the gyro is designed as an electronically driven tuning fork, often fabricated out of a single piece of quartz or silicon. Such gyros operate in accordance with the dynamic theory that when an angle rate is applied to a translating body, a Coriolis force is generated.
This system is usually integrated on a silicon chip. It has two mass-balanced quartz tuning forks, arranged "handle-to-handle" so forces cancel. Aluminum electrodes evaporated onto the forks and the underlying chip both drive and sense the motion. The system is both manufacturable and inexpensive. Since quartz is dimensionally stable, the system can be accurate.
As the forks are twisted about the axis of the handle, the vibration of the tines tends to continue in the same plane of motion. This motion has to be resisted by electrostatic forces from the electrodes under the tines. By measuring the difference in capacitance between the two tines of a fork, the system can determine the rate of angular motion.
Current state-of-the-art non-military technology (as of 2005[update]) can build small solid-state sensors that can measure human body movements. These devices have no moving parts and weigh about 50 grams (2 ounces).
Solid-state devices using the same physical principles are used for image stabilization in small cameras or camcorders. These can be extremely small, around 5 millimetres (0.20 inches) and are built with microelectromechanical systems (MEMS) technologies.[26]
MHD sensor
[edit]Sensors based on magnetohydrodynamic principles can be used to measure angular velocities.
MEMS gyroscope
[edit]
MEMS gyroscopes typically rely on the Coriolis effect to measure angular velocity. It consists of a resonating proof mass mounted in silicon. The gyroscope is, unlike an accelerometer, an active sensor. The proof mass is pushed back and forth by driving combs. A rotation of the gyroscope generates a Coriolis force that is acting on the mass which results in a motion in a different direction. The motion in this direction is measured by electrodes and represents the rate of turn.[27]
Ring laser gyros
[edit]
A ring laser gyro (RLG) splits a beam of laser light into two beams in opposite directions through narrow tunnels in a closed circular optical path around the perimeter of a triangular block of temperature-stable Cervit glass with reflecting mirrors placed in each corner. When the gyro is rotating at some angular rate, the distance traveled by each beam will differ—the shorter path being opposite to the rotation. The phase shift between the two beams can be measured by an interferometer and is proportional to the rate of rotation (Sagnac effect).
In practice, at low rotation rates the output frequency can drop to zero as the result of backscattering causing the beams to synchronise and lock together. This is known as a lock-in, or laser-lock. The result is that there is no change in the interference pattern and therefore no measurement change.
To unlock the counter-rotating light beams, laser gyros either have independent light paths for the two directions (usually in fiber optic gyros), or the laser gyro is mounted on a piezo-electric dither motor that rapidly vibrates the laser ring back and forth about its input axis through the lock-in region to decouple the light waves.
The shaker is the most accurate, because both light beams use exactly the same path. Thus laser gyros retain moving parts, but they do not move as far.
Fiber optic gyros
[edit]A more recent variation on the optical gyroscope, the fiber optic gyroscope (FOG), uses an external laser and two beams going opposite directions (counter-propagating) in long spools (several kilometers) of fiber optic filament, with the phase difference of the two beams compared after their travel through the spools of fiber.
The basic mechanism, monochromatic laser light travelling in opposite paths and the Sagnac effect, is the same in a FOG and a RLG, but the engineering details are substantially different in the FOG compared to earlier laser gyros.
Precise winding of the fiber-optic coil is required to ensure the paths taken by the light in opposite directions are as similar as possible. The FOG requires more complex calibrations than a laser ring gyro making the development and manufacture of FOG's more technically challenging that for a RLG. However FOG's do not suffer from laser lock at low speeds and do not need to contain any moving parts, increasing the maximum potential accuracy and lifespan of a FOG over an equivalent RLG.
Pendular accelerometers
[edit]
The basic, open-loop accelerometer consists of a mass attached to a spring. The mass is constrained to move only in line with the spring. Acceleration causes deflection of the mass and the offset distance is measured. The acceleration is derived from the values of deflection distance, mass and the spring constant. The system must also be damped to avoid oscillation. A closed-loop accelerometer achieves higher performance by using a feedback loop to cancel the deflection, thus keeping the mass nearly stationary. Whenever the mass deflects, the feedback loop causes an electric coil to apply an equally negative force on the mass, canceling the motion. Acceleration is derived from the amount of negative force applied. Because the mass barely moves, the effects of non-linearities of the spring and damping system are greatly reduced. In addition, this accelerometer provides for increased bandwidth beyond the natural frequency of the sensing element.
Both types of accelerometers have been manufactured as integrated micro-machinery on silicon chips.
TIMU sensors
[edit]DARPA's Microsystems Technology Office (MTO) department is working on a Micro-PNT (Micro-Technology for Positioning, Navigation and Timing) program to design Timing & Inertial Measurement Unit (TIMU) chips that do absolute position tracking on a single chip without GPS-aided navigation.[28][29][30]
Micro-PNT adds a highly accurate master timing clock[31] integrated into an IMU (Inertial Measurement Unit) chip, making it a Timing & Inertial Measurement Unit chip. A TIMU chip integrates 3-axis gyroscope, 3-axis accelerometer and 3-axis magnetometer together with a highly accurate master timing clock, so that it can simultaneously measure the motion tracked and combine that with timing from the synchronized clock.[28][29]
Method
[edit]In one form, the navigational system of equations acquires linear and angular measurements from the inertial and body frame, respectively and calculates the final attitude and position in the NED frame of reference.
Where f is specific force, is angular rate, a is acceleration, R is position, and V are velocity, is the angular velocity of the earth, g is the acceleration due to gravity, and h are the NED location parameters. Also, super/subscripts of E, I and B are representing variables in the Earth centered, inertial or body reference frame, respectively and C is a transformation of reference frames.[citation needed]
See also
[edit]- Index of aviation articles
- Spacecraft attitude control – Process of controlling orientation of an aerospace vehicle
- LN-3 inertial navigation system
- Quantum compass
References
[edit]- ^ "Basic Principles of Inertial Navigation Seminar on inertial navigation systems" (PDF). AeroStudents.com. Tampere University of Technology, page 5. Archived (PDF) from the original on 25 October 2023. Retrieved 17 April 2018.
- ^ Bruno Siciliano; Oussama Khatib (20 May 2008). Springer Handbook of Robotics. Springer Science & Business Media. ISBN 978-3-540-23957-4.
- ^ Gerald Cook (14 October 2011). Mobile Robots: Navigation, Control and Remote Sensing. John Wiley & Sons. ISBN 978-1-118-02904-6.
- ^ "NASA.gov". Archived from the original on 4 April 2023. Retrieved 26 January 2021.
- ^ Wan Mohd Yaakob Wan Bejuri, Mohd Murtadha Mohamad, Hadri Omar, Farhana Syed Omar and Nurfarah Ain Limin (2019). Robust Special Strategies Resampling for Mobile Inertial Navigation Systems. International Journal of Innovative Technology and Exploring Engineering. Vol. 9(2), pp. 3196–3024,See publication here
- ^ Wan Mohd Yaakob Wan Bejuri, Mohd Murtadha Mohamad, Raja Zahilah Raja Mohd Radzi, Sheikh Hussain Shaikh Salleh (2019). An Improved Resampling Scheme for Particle Filtering in Inertial Navigation System. Lecture Notes in Computer Science. Vol. 11432, pp. 555–563,See publication here
- ^ Sandeep Kumar Shukla; Jean-Pierre Talpin (5 August 2010). Synthesis of Embedded Software: Frameworks and Methodologies for Correctness by Construction. Springer Science & Business Media. p. 62. ISBN 978-1-4419-6400-7.
- ^ Inertial navigation systems analysis, Kenneth R. Britting, Wiley-Interscience, 1971.
- ^ Calculated from reversing S=1/2.a.t^2 into t=√(2s/a), where s=distance in meters, a is acceleration (here 9.8 times g), and t is time in seconds.
- ^ Applied Optimal Estimation, Arthur Gelb (Editor), M.I.T. Press, 1974.
- ^ "GPS.gov: Information About GPS Jamming". www.gps.gov. Retrieved 30 July 2018.
- ^ Fairfax, Luisa; Fresconi, Frank (April 2012). "Position Estimation for Projectiles Using Low-cost Sensors and Flight Dynamics" (PDF). Archived (PDF) from the original on 2 May 2017.
- ^ "Securing military GPS from spoofing and jamming vulnerabilities". Military Embedded Systems. Retrieved 30 July 2018.
- ^ "New guided munition sensors are greater than sum of their parts". www.army.mil. Retrieved 30 July 2018.
- ^ "Sputnik Biographies—Wernher von Braun (1912–1977)". history.nasa.gov. Archived from the original on 28 March 2009.
- ^ "Engineering360". Globalspec.com. Archived from the original on 20 June 2010.
- ^ Battin, R. H. (1982). "Space guidance evolution – A personal narrative". Journal of Guidance, Control, and Dynamics. 5 (2): 97. Bibcode:1982JGCD....5...97B. doi:10.2514/3.19761.
- ^ Neufeld, Jacob. "Technology Push". history.navy.mil. Archived from the original on 12 December 2012. Retrieved 9 July 2017.
- ^ MacKenzie, Donald A. (1993). Inventing Accuracy: A Historical Sociology of Nuclear Missile Guidance. MIT Press. p. 22. ISBN 978-0-262-63147-1.
- ^ Apollo on-board guidance, navigation and control system, Dave Hoag, International Space Hall of Fame Dedication Conference in Alamogordo, N.M., October 1976
- ^ C. S. Draper; W. Wrigley; G. Hoag; R. H. Battin; J. E. Miller; D. A. Koso; Dr. A. L. Hopkins; Dr. W. E. Vander Velde (June 1965). "Apollo Guidance and Navigation" (PDF). Web.mit.edu. Archived (PDF) from the original on 11 June 2016. Retrieved 9 July 2017.
- ^ Eshbach's Handbook of Engineering Fundamentals By Ovid W. Eshbach, Byron pg 9
- ^ Weed, D.; Broderick, J.; Love, J.; Ryno, T. (2004). "GPS Align In Motion of civilian strapdown INS". PLANS 2004. Position Location and Navigation Symposium (IEEE Cat. No.04CH37556). pp. 184–192. doi:10.1109/PLANS.2004.1308992. ISBN 0-7803-8416-4. S2CID 28811547.
- ^ "The Hemispherical Resonator Gyro: From Wineglass to the Planets, David M. Rozelle" (PDF). Northropgrumman.com. Archived (PDF) from the original on 21 September 2013.
- ^ Defaiya, Al (4 May 2017). "Safran Logs 3,000 Orders for HRG-Based Navigation Systems". Defaiya.com. Archived from the original on 19 August 2017. Retrieved 19 August 2017.
- ^ "Epson Toyocom Quartz Gyro sensors – How they work and what's ahead". Findmems.com. Archived from the original on 16 January 2014.
- ^ "Gyroscopes". Xsens 3D motion tracking. Archived from the original on 22 January 2019. Retrieved 22 January 2019.
- ^ a b "Micro-Technology for Positioning, Navigation and Timing (Micro-PNT)". darpa.mil. Archived from the original on 5 May 2017. Retrieved 9 July 2017.
- ^ a b Extreme Miniaturization: Seven Devices, One Chip to Navigate without GPS Archived 7 March 2017 at the Wayback Machine
- ^ "Microfabrication methods to help navigate a day without GPS". darpa.mil. Archived from the original on 30 June 2013. Retrieved 9 July 2017.
- ^ "Clocks". darpa.mil. Archived from the original on 17 May 2017. Retrieved 9 July 2017.
Further reading
[edit]- Zanetti, Renato; d'Souza, Christopher (2020), "Inertial Navigation", Encyclopedia of Systems and Control, pp. 1–7, doi:10.1007/978-1-4471-5102-9_100036-1, ISBN 978-1-4471-5102-9
- A.D. King (1998). "Inertial Navigation – Forty Years of Evolution" (PDF). GEC Review. 13 (3). General Electric Company plc: 140–149.
- E. v. Hinueber (iMAR Navigation) (2011). "Design of an Unaided Aircraft Attitude Reference System with Medium Accurate Gyroscopes for Higher Performance Attitude Requirements". Inertial Sensors and Systems, Symposium Gyro Technology, Karlsruhe / Germany. 2011. iMAR Navigation / DGON.
External links
[edit]- Ferranti Inertial Navigation System (INAS)
- Inertial Navigation System
- Principle of operation of an accelerometer
- Overview of inertial instrument types
- Oxford Technical Solutions Inertial Navigation Guide
- Listing of open-source Inertial Navigation system
- Impact of inertial sensor errors on Inertial Navigation System position and attitude errors
- Introduction to Inertial Navigation Systems in UAV/Drone Applications





