Technique of integral evaluation
In mathematics , a trigonometric substitution replaces a trigonometric function for another expression. In calculus , trigonometric substitutions are a technique for evaluating integrals. In this case, an expression involving a radical function is replaced with a trigonometric one. Trigonometric identities may help simplify the answer.[ 1] [ 2]
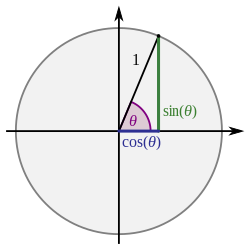
a 2 − x 2 [ edit ] Let
x
=
a
sin
θ
,
{\displaystyle x=a\sin \theta ,}
identity
1
−
sin
2
θ
=
cos
2
θ
.
{\displaystyle 1-\sin ^{2}\theta =\cos ^{2}\theta .}
Geometric construction for Case I In the integral
∫
d
x
a
2
−
x
2
,
{\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}},}
we may use
x
=
a
sin
θ
,
d
x
=
a
cos
θ
d
θ
,
θ
=
arcsin
x
a
.
{\displaystyle x=a\sin \theta ,\quad dx=a\cos \theta \,d\theta ,\quad \theta =\arcsin {\frac {x}{a}}.}
Then,
∫
d
x
a
2
−
x
2
=
∫
a
cos
θ
d
θ
a
2
−
a
2
sin
2
θ
=
∫
a
cos
θ
d
θ
a
2
(
1
−
sin
2
θ
)
=
∫
a
cos
θ
d
θ
a
2
cos
2
θ
=
∫
d
θ
=
θ
+
C
=
arcsin
x
a
+
C
.
{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&=\arcsin {\frac {x}{a}}+C.\end{aligned}}}
The above step requires that
a
>
0
{\displaystyle a>0}
cos
θ
>
0.
{\displaystyle \cos \theta >0.}
a
{\displaystyle a}
a
2
,
{\displaystyle a^{2},}
−
π
/
2
<
θ
<
π
/
2
{\displaystyle -\pi /2<\theta <\pi /2}
For a definite integral, one must figure out how the bounds of integration change. For example, as
x
{\displaystyle x}
0
{\displaystyle 0}
a
/
2
,
{\displaystyle a/2,}
sin
θ
{\displaystyle \sin \theta }
0
{\displaystyle 0}
1
/
2
,
{\displaystyle 1/2,}
θ
{\displaystyle \theta }
0
{\displaystyle 0}
π
/
6.
{\displaystyle \pi /6.}
∫
0
a
/
2
d
x
a
2
−
x
2
=
∫
0
π
/
6
d
θ
=
π
6
.
{\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.}
Some care is needed when picking the bounds. Because integration above requires that
−
π
/
2
<
θ
<
π
/
2
{\displaystyle -\pi /2<\theta <\pi /2}
θ
{\displaystyle \theta }
0
{\displaystyle 0}
π
/
6.
{\displaystyle \pi /6.}
θ
{\displaystyle \theta }
π
{\displaystyle \pi }
5
π
/
6
,
{\displaystyle 5\pi /6,}
Alternatively, fully evaluate the indefinite integrals before applying the boundary conditions. In that case, the antiderivative gives
∫
0
a
/
2
d
x
a
2
−
x
2
=
arcsin
(
x
a
)
|
0
a
/
2
=
arcsin
(
1
2
)
−
arcsin
(
0
)
=
π
6
{\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\arcsin \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}=\arcsin \left({\frac {1}{2}}\right)-\arcsin(0)={\frac {\pi }{6}}}
The integral
∫
a
2
−
x
2
d
x
,
{\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx,}
may be evaluated by letting
x
=
a
sin
θ
,
d
x
=
a
cos
θ
d
θ
,
θ
=
arcsin
x
a
,
{\textstyle x=a\sin \theta ,\,dx=a\cos \theta \,d\theta ,\,\theta =\arcsin {\dfrac {x}{a}},}
a
>
0
{\displaystyle a>0}
a
2
=
a
,
{\textstyle {\sqrt {a^{2}}}=a,}
−
π
/
2
≤
θ
≤
π
/
2
{\textstyle -\pi /2\leq \theta \leq \pi /2}
cos
θ
≥
0
{\displaystyle \cos \theta \geq 0}
cos
2
θ
=
cos
θ
.
{\textstyle {\sqrt {\cos ^{2}\theta }}=\cos \theta .}
Then,
∫
a
2
−
x
2
d
x
=
∫
a
2
−
a
2
sin
2
θ
(
a
cos
θ
)
d
θ
=
∫
a
2
(
1
−
sin
2
θ
)
(
a
cos
θ
)
d
θ
=
∫
a
2
(
cos
2
θ
)
(
a
cos
θ
)
d
θ
=
∫
(
a
cos
θ
)
(
a
cos
θ
)
d
θ
=
a
2
∫
cos
2
θ
d
θ
=
a
2
∫
(
1
+
cos
2
θ
2
)
d
θ
=
a
2
2
(
θ
+
1
2
sin
2
θ
)
+
C
=
a
2
2
(
θ
+
sin
θ
cos
θ
)
+
C
=
a
2
2
(
arcsin
x
a
+
x
a
1
−
x
2
a
2
)
+
C
=
a
2
2
arcsin
x
a
+
x
2
a
2
−
x
2
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}}
For a definite integral, the bounds change once the substitution is performed and are determined using the equation
θ
=
arcsin
x
a
,
{\textstyle \theta =\arcsin {\dfrac {x}{a}},}
−
π
/
2
≤
θ
≤
π
/
2.
{\textstyle -\pi /2\leq \theta \leq \pi /2.}
For example, the definite integral
∫
−
1
1
4
−
x
2
d
x
,
{\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx,}
may be evaluated by substituting
x
=
2
sin
θ
,
d
x
=
2
cos
θ
d
θ
,
{\displaystyle x=2\sin \theta ,\,dx=2\cos \theta \,d\theta ,}
θ
=
arcsin
x
2
.
{\textstyle \theta =\arcsin {\dfrac {x}{2}}.}
Because
arcsin
(
1
/
2
)
=
π
/
6
{\displaystyle \arcsin(1/{2})=\pi /6}
arcsin
(
−
1
/
2
)
=
−
π
/
6
,
{\displaystyle \arcsin(-1/2)=-\pi /6,}
∫
−
1
1
4
−
x
2
d
x
=
∫
−
π
/
6
π
/
6
4
−
4
sin
2
θ
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
4
(
1
−
sin
2
θ
)
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
4
(
cos
2
θ
)
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
(
2
cos
θ
)
(
2
cos
θ
)
d
θ
=
4
∫
−
π
/
6
π
/
6
cos
2
θ
d
θ
=
4
∫
−
π
/
6
π
/
6
(
1
+
cos
2
θ
2
)
d
θ
=
2
[
θ
+
1
2
sin
2
θ
]
−
π
/
6
π
/
6
=
[
2
θ
+
sin
2
θ
]
|
−
π
/
6
π
/
6
=
(
π
3
+
sin
π
3
)
−
(
−
π
3
+
sin
(
−
π
3
)
)
=
2
π
3
+
3
.
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\sin 2\theta \right]_{-\pi /6}^{\pi /6}=[2\theta +\sin 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}}
On the other hand, direct application of the boundary terms to the previously obtained formula for the antiderivative yields
∫
−
1
1
4
−
x
2
d
x
=
[
2
2
2
arcsin
x
2
+
x
2
2
2
−
x
2
]
−
1
1
=
(
2
arcsin
1
2
+
1
2
4
−
1
)
−
(
2
arcsin
(
−
1
2
)
+
−
1
2
4
−
1
)
=
(
2
⋅
π
6
+
3
2
)
−
(
2
⋅
(
−
π
6
)
−
3
2
)
=
2
π
3
+
3
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[{\frac {2^{2}}{2}}\arcsin {\frac {x}{2}}+{\frac {x}{2}}{\sqrt {2^{2}-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}
a 2 + x 2 [ edit ] Let
x
=
a
tan
θ
,
{\displaystyle x=a\tan \theta ,}
1
+
tan
2
θ
=
sec
2
θ
.
{\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta .}
Examples of Case II [ edit ] Geometric construction for Case II In the integral
∫
d
x
a
2
+
x
2
{\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}}
we may write
x
=
a
tan
θ
,
d
x
=
a
sec
2
θ
d
θ
,
θ
=
arctan
x
a
,
{\displaystyle x=a\tan \theta ,\quad dx=a\sec ^{2}\theta \,d\theta ,\quad \theta =\arctan {\frac {x}{a}},}
so that the integral becomes
∫
d
x
a
2
+
x
2
=
∫
a
sec
2
θ
d
θ
a
2
+
a
2
tan
2
θ
=
∫
a
sec
2
θ
d
θ
a
2
(
1
+
tan
2
θ
)
=
∫
a
sec
2
θ
d
θ
a
2
sec
2
θ
=
∫
d
θ
a
=
θ
a
+
C
=
1
a
arctan
x
a
+
C
,
{\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\[6pt]&=\int {\frac {d\theta }{a}}\\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}}
provided
a
≠
0.
{\displaystyle a\neq 0.}
For a definite integral, the bounds change once the substitution is performed and are determined using the equation
θ
=
arctan
x
a
,
{\displaystyle \theta =\arctan {\frac {x}{a}},}
−
π
2
<
θ
<
π
2
.
{\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}.}
For example, the definite integral
∫
0
1
4
d
x
1
+
x
2
{\displaystyle \int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,}
may be evaluated by substituting
x
=
tan
θ
,
d
x
=
sec
2
θ
d
θ
,
{\displaystyle x=\tan \theta ,\,dx=\sec ^{2}\theta \,d\theta ,}
θ
=
arctan
x
.
{\displaystyle \theta =\arctan x.}
Since
arctan
0
=
0
{\displaystyle \arctan 0=0}
arctan
1
=
π
/
4
,
{\displaystyle \arctan 1=\pi /4,}
∫
0
1
4
d
x
1
+
x
2
=
4
∫
0
1
d
x
1
+
x
2
=
4
∫
0
π
/
4
sec
2
θ
d
θ
1
+
tan
2
θ
=
4
∫
0
π
/
4
sec
2
θ
d
θ
sec
2
θ
=
4
∫
0
π
/
4
d
θ
=
(
4
θ
)
|
0
π
/
4
=
4
(
π
4
−
0
)
=
π
.
{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}}
Meanwhile, direct application of the boundary terms to the formula for the antiderivative yields
∫
0
1
4
d
x
1
+
x
2
=
4
∫
0
1
d
x
1
+
x
2
=
4
[
1
1
arctan
x
1
]
0
1
=
4
(
arctan
x
)
|
0
1
=
4
(
arctan
1
−
arctan
0
)
=
4
(
π
4
−
0
)
=
π
,
{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\left[{\frac {1}{1}}\arctan {\frac {x}{1}}\right]_{0}^{1}\\[6pt]&=4(\arctan x){\Bigg |}_{0}^{1}\\[6pt]&=4(\arctan 1-\arctan 0)\\[6pt]&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}}
The integral
∫
a
2
+
x
2
d
x
{\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}}
may be evaluated by letting
x
=
a
tan
θ
,
d
x
=
a
sec
2
θ
d
θ
,
θ
=
arctan
x
a
,
{\displaystyle x=a\tan \theta ,\,dx=a\sec ^{2}\theta \,d\theta ,\,\theta =\arctan {\frac {x}{a}},}
where
a
>
0
{\displaystyle a>0}
a
2
=
a
,
{\displaystyle {\sqrt {a^{2}}}=a,}
−
π
2
<
θ
<
π
2
{\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}}
sec
θ
>
0
{\displaystyle \sec \theta >0}
sec
2
θ
=
sec
θ
.
{\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta .}
Then,
∫
a
2
+
x
2
d
x
=
∫
a
2
+
a
2
tan
2
θ
(
a
sec
2
θ
)
d
θ
=
∫
a
2
(
1
+
tan
2
θ
)
(
a
sec
2
θ
)
d
θ
=
∫
a
2
sec
2
θ
(
a
sec
2
θ
)
d
θ
=
∫
(
a
sec
θ
)
(
a
sec
2
θ
)
d
θ
=
a
2
∫
sec
3
θ
d
θ
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}
integral of secant cubed may be evaluated using integration by parts . As a result,
∫
a
2
+
x
2
d
x
=
a
2
2
(
sec
θ
tan
θ
+
ln
|
sec
θ
+
tan
θ
|
)
+
C
=
a
2
2
(
1
+
x
2
a
2
⋅
x
a
+
ln
|
1
+
x
2
a
2
+
x
a
|
)
+
C
=
1
2
(
x
a
2
+
x
2
+
a
2
ln
|
x
+
a
2
+
x
2
a
|
)
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
x 2 − a 2 [ edit ] Let
x
=
a
sec
θ
,
{\displaystyle x=a\sec \theta ,}
sec
2
θ
−
1
=
tan
2
θ
.
{\displaystyle \sec ^{2}\theta -1=\tan ^{2}\theta .}
Examples of Case III [ edit ] Geometric construction for Case III Integrals such as
∫
d
x
x
2
−
a
2
{\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}}
can also be evaluated by partial fractions rather than trigonometric substitutions. However, the integral
∫
x
2
−
a
2
d
x
{\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx}
cannot. In this case, an appropriate substitution is:
x
=
a
sec
θ
,
d
x
=
a
sec
θ
tan
θ
d
θ
,
θ
=
arcsec
x
a
,
{\displaystyle x=a\sec \theta ,\,dx=a\sec \theta \tan \theta \,d\theta ,\,\theta =\operatorname {arcsec} {\frac {x}{a}},}
where
a
>
0
{\displaystyle a>0}
a
2
=
a
,
{\displaystyle {\sqrt {a^{2}}}=a,}
0
≤
θ
<
π
2
{\displaystyle 0\leq \theta <{\frac {\pi }{2}}}
x
>
0
,
{\displaystyle x>0,}
tan
θ
≥
0
{\displaystyle \tan \theta \geq 0}
tan
2
θ
=
tan
θ
.
{\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta .}
Then,
∫
x
2
−
a
2
d
x
=
∫
a
2
sec
2
θ
−
a
2
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
(
sec
2
θ
−
1
)
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
tan
2
θ
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
sec
θ
tan
2
θ
d
θ
=
a
2
∫
(
sec
θ
)
(
sec
2
θ
−
1
)
d
θ
=
a
2
∫
(
sec
3
θ
−
sec
θ
)
d
θ
.
{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta .\end{aligned}}}
One may evaluate the integral of the secant function by multiplying the numerator and denominator by
(
sec
θ
+
tan
θ
)
{\displaystyle (\sec \theta +\tan \theta )}
integral of secant cubed by parts.[ 3]
∫
x
2
−
a
2
d
x
=
a
2
2
(
sec
θ
tan
θ
+
ln
|
sec
θ
+
tan
θ
|
)
−
a
2
ln
|
sec
θ
+
tan
θ
|
+
C
=
a
2
2
(
sec
θ
tan
θ
−
ln
|
sec
θ
+
tan
θ
|
)
+
C
=
a
2
2
(
x
a
⋅
x
2
a
2
−
1
−
ln
|
x
a
+
x
2
a
2
−
1
|
)
+
C
=
1
2
(
x
x
2
−
a
2
−
a
2
ln
|
x
+
x
2
−
a
2
a
|
)
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
When
π
2
<
θ
≤
π
,
{\displaystyle {\frac {\pi }{2}}<\theta \leq \pi ,}
x
<
0
{\displaystyle x<0}
tan
θ
≤
0
,
{\displaystyle \tan \theta \leq 0,}
tan
2
θ
=
−
tan
θ
{\displaystyle {\sqrt {\tan ^{2}\theta }}=-\tan \theta }
Substitutions that eliminate trigonometric functions [ edit ] Substitution can be used to remove trigonometric functions.
For instance,
∫
f
(
sin
(
x
)
,
cos
(
x
)
)
d
x
=
∫
1
±
1
−
u
2
f
(
u
,
±
1
−
u
2
)
d
u
u
=
sin
(
x
)
∫
f
(
sin
(
x
)
,
cos
(
x
)
)
d
x
=
∫
1
∓
1
−
u
2
f
(
±
1
−
u
2
,
u
)
d
u
u
=
cos
(
x
)
∫
f
(
sin
(
x
)
,
cos
(
x
)
)
d
x
=
∫
2
1
+
u
2
f
(
2
u
1
+
u
2
,
1
−
u
2
1
+
u
2
)
d
u
u
=
tan
(
x
2
)
{\displaystyle {\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\frac {x}{2}}\right)\\[6pt]\end{aligned}}}
The last substitution is known as the Weierstrass substitution , which makes use of tangent half-angle formulas .
For example,
∫
4
cos
x
(
1
+
cos
x
)
3
d
x
=
∫
2
1
+
u
2
4
(
1
−
u
2
1
+
u
2
)
(
1
+
1
−
u
2
1
+
u
2
)
3
d
u
=
∫
(
1
−
u
2
)
(
1
+
u
2
)
d
u
=
∫
(
1
−
u
4
)
d
u
=
u
−
u
5
5
+
C
=
tan
x
2
−
1
5
tan
5
x
2
+
C
.
{\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du=u-{\frac {u^{5}}{5}}+C=\tan {\frac {x}{2}}-{\frac {1}{5}}\tan ^{5}{\frac {x}{2}}+C.\end{aligned}}}
Hyperbolic substitution [ edit ] Substitutions of hyperbolic functions can also be used to simplify integrals.[ 4]
For example, to integrate
1
/
a
2
+
x
2
{\displaystyle 1/{\sqrt {a^{2}+x^{2}}}}
x
=
a
sinh
u
{\displaystyle x=a\sinh {u}}
d
x
=
a
cosh
u
d
u
{\displaystyle dx=a\cosh u\,du}
the identity
cosh
2
(
x
)
−
sinh
2
(
x
)
=
1
{\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1}
to find:
∫
d
x
a
2
+
x
2
=
∫
a
cosh
u
d
u
a
2
+
a
2
sinh
2
u
=
∫
cosh
u
d
u
1
+
sinh
2
u
=
∫
cosh
u
cosh
u
d
u
=
u
+
C
=
sinh
−
1
x
a
+
C
.
{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\\[6pt]&=\int {\frac {\cosh {u}\,du}{\sqrt {1+\sinh ^{2}{u}}}}\\[6pt]&=\int {\frac {\cosh {u}}{\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C.\end{aligned}}}
If desired, this result may be further transformed using other identities, such as using the relation
sinh
−
1
z
=
arsinh
z
=
ln
(
z
+
z
2
+
1
)
{\displaystyle \sinh ^{-1}{z}=\operatorname {arsinh} {z}=\ln(z+{\sqrt {z^{2}+1}})}
:
sinh
−
1
x
a
+
C
=
ln
(
x
a
+
x
2
a
2
+
1
)
+
C
=
ln
(
x
+
x
2
+
a
2
a
)
+
C
.
{\displaystyle {\begin{aligned}\sinh ^{-1}{\frac {x}{a}}+C&=\ln \left({\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}+1}}\,\right)+C\\[6pt]&=\ln \left({\frac {x+{\sqrt {x^{2}+a^{2}}}}{a}}\,\right)+C.\end{aligned}}}









![{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}(1-\sin ^{2}\theta )}}}\\[6pt]&=\int {\frac {a\cos \theta \,d\theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&=\arcsin {\frac {x}{a}}+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb0f45f461035d567bc90912abb383b4f184bc87)






















![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\sin ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\sin ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\sin 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\sin \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left(\arcsin {\frac {x}{a}}+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\arcsin {\frac {x}{a}}+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dc8b7727d973d3575d22f781010591f86e20436)







![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\sin ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\sin ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\sin 2\theta \right]_{-\pi /6}^{\pi /6}=[2\theta +\sin 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\sin {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\sin \left(-{\frac {\pi }{3}}\right)\right)={\frac {2\pi }{3}}+{\sqrt {3}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00648715967922d2740a30e742875ae05a2a32ba)
![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[{\frac {2^{2}}{2}}\arcsin {\frac {x}{2}}+{\frac {x}{2}}{\sqrt {2^{2}-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\arcsin {\frac {1}{2}}+{\frac {1}{2}}{\sqrt {4-1}}\right)-\left(2\arcsin \left(-{\frac {1}{2}}\right)+{\frac {-1}{2}}{\sqrt {4-1}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331bd80b5e0c5a19ece342b80e800bd3d1bc2093)




![{\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}(1+\tan ^{2}\theta )}}\\[6pt]&=\int {\frac {a\sec ^{2}\theta \,d\theta }{a^{2}\sec ^{2}\theta }}\\[6pt]&=\int {\frac {d\theta }{a}}\\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan {\frac {x}{a}}+C,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c65e486a1f8cafb8397f72820972c35efacd858)








![{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{1+\tan ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta \,d\theta }{\sec ^{2}\theta }}\\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=(4\theta ){\Bigg |}_{0}^{\pi /4}=4\left({\frac {\pi }{4}}-0\right)=\pi .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1fdc8a13ac2312f87a1c7b36cef5ca23eb89075)
![{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4\,dx}{1+x^{2}}}\,&=4\int _{0}^{1}{\frac {dx}{1+x^{2}}}\\[6pt]&=4\left[{\frac {1}{1}}\arctan {\frac {x}{1}}\right]_{0}^{1}\\[6pt]&=4(\arctan x){\Bigg |}_{0}^{1}\\[6pt]&=4(\arctan 1-\arctan 0)\\[6pt]&=4\left({\frac {\pi }{4}}-0\right)=\pi ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6316f33eb7e2b8fb35378d35b8f9e6543f92e2f)






![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/108a5f1becea83b5cb41021d81544ff3e1bab889)
![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|{\frac {x+{\sqrt {a^{2}+x^{2}}}}{a}}\right|\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35b28bc818f9ffcffedfb2e767d2d578c4a3e038)











![{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d551bea9f1a33df981d45ab8cf11a1443d6da85)




![{\displaystyle {\begin{aligned}\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\sin(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\sin(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\frac {x}{2}}\right)\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54ec70f26a22afa5b02ffb9893d5e33e4f23edf1)





![{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}+x^{2}}}}&=\int {\frac {a\cosh u\,du}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\\[6pt]&=\int {\frac {\cosh {u}\,du}{\sqrt {1+\sinh ^{2}{u}}}}\\[6pt]&=\int {\frac {\cosh {u}}{\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca1b341ada3943f7c78484e1a58a2c5b20524d70)

![{\displaystyle {\begin{aligned}\sinh ^{-1}{\frac {x}{a}}+C&=\ln \left({\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}+1}}\,\right)+C\\[6pt]&=\ln \left({\frac {x+{\sqrt {x^{2}+a^{2}}}}{a}}\,\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20441614472c3f5e71a8f449e4cef1cddfd2d0dc)