Jump to content

Hamilton's optico-mechanical analogy

From Wikipedia, the free encyclopedia

Hamiltonian Optics—Rays and Wavefronts

Hamilton's optico-mechanical analogy is a conceptual parallel between trajectories in classical mechanics and wavefronts in optics, introduced by William Rowan Hamilton around 1831.[1] It may be viewed as linking Huygens' principle of optics with Maupertuis' principle of mechanics.[2][3][4][5][6]

While Hamilton discovered the analogy in 1831, it was not applied practically until Hans Busch used it to explain electron beam focusing in 1925.[7] According to Cornelius Lanczos, the analogy has been important in the development of ideas in quantum physics.[3] Erwin Schrödinger cites the analogy in the very first sentence of his paper introducing his wave mechanics.[8] Later in the body of his paper he says:

Unfortunately this powerful and momentous conception of Hamilton is deprived, in most modern reproductions, of its beautiful raiment as a superfluous accessory, in favour of a more colourless representation of the analytical correspondence.[9]

Quantitative and formal analysis based on the analogy use the Hamilton–Jacobi equation; conversely the analogy provides an alternative and more accessible path for introducing the Hamilton–Jacobi equation approach to mechanics. The orthogonality of mechanical trajectories characteristic of geometrical optics to the optical wavefronts characteristic of a full wave equation, resulting from the variational principle, leads to the corresponding differential equations.[10]

Hamilton's analogy

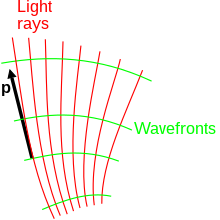
[edit]

The propagation of light can be considered in terms of rays and wavefronts in ordinary physical three-dimensional space. The wavefronts are two-dimensional curved surfaces; the rays are one-dimensional curved lines.[11] Hamilton's analogy amounts to two interpretations of a figure like the one shown here. In the optical interpretation, the green wavefronts are lines of constant phase and the orthogonal red lines are the rays of geometrical optics. In the mechanical interpretation, the green lines denote constant values of action derived by applying Hamilton's principle to mechanical motion and the red lines are the orthogonal object trajectories.[11]

The orthogonality of the wavefronts to rays (or equal-action surfaces to trajectories) means we can compute one set from the other set.[10] This explains how Kirchhoff's diffraction formula predicts a wave phenomenon – diffraction – using only geometrical ray tracing.[7]: 745  Rays traced from the source to an aperture give a wavefront that becomes sources for rays reaching the diffraction pattern where they are summed using complex phases from the orthogonal wavefronts.

The wavefronts and rays or the equal-action surfaces and trajectories are dual objects linked by orthogonality.[10] On one hand, a ray can be regarded as the orbit of a particle of light. It successively punctures the wave surfaces. The successive punctures can be regarded as defining the trajectory of the particle. On the other hand, a wave-front can be regarded as a level surface of displacement of some quantity, such as electric field intensity, hydrostatic pressure, particle number density, oscillatory phase, or probability amplitude. Then the physical meaning of the rays is less evident.[12]

Huygen's principle; Fermat's principle

[edit]

The Hamilton optico-mechanical analogy is closely related to Fermat's principle and thus to the Huygens–Fresnel principle.[10] Fermat's principle states that the rays between wavefronts will take the path least time; the concept of successive wavefronts derives from Huygens principle.

Extended Huygens' principle

[edit]

Going beyond ordinary three-dimensional physical space, one can imagine a higher dimensional abstract configuration "space", with a dimension a multiple of 3. In this space, one can imagine again rays as one-dimensional curved lines. Now the wavefronts are hypersurfaces of dimension one less than the dimension of the space.[6] Such a multi-dimensional space can serve as a configuration space for a multi-particle system.

Classical limit of the Schrödinger equation

[edit]

Albert Messiah considers a classical limit of the Schrödinger equation. He finds there an optical analogy. The trajectories of his particles are orthogonal to the surfaces of equal phase. He writes "In the language of optics, the latter are the wave fronts, and the trajectories of the particles are the rays. Hence the classical approximation is equivalent to the geometric optics approximation: we find once again, as a consequence of the Schrödinger equation, the basic postulate of the theory of matter waves."[13]

History

[edit]

Hamilton's optico-mechanical analogy played a critical part[14][11] in the thinking of Schrödinger, one of the originators of quantum mechanics. Section 1 of his paper published in December 1926 is titled "The Hamiltonian analogy between mechanics and optics".[15] Section 1 of the first of his four lectures on wave mechanics delivered in 1928 is titled "Derivation of the fundamental idea of wave mechanics from Hamilton's analogy between ordinary mechanics and geometrical optics".[16]

In a brief paper in 1923, de Broglie wrote : "Dynamics must undergo the same evolution that optics has undergone when undulations took the place of purely geometrical optics."[17] In his 1924 thesis, though Louis de Broglie did not name the optico-mechanical analogy, he wrote in his introduction,[18]

... a single principle, that of Maupertuis, and later in another form as Hamilton's Principle of least action ... Fermat's ... principle ..., which nowadays is usually called the principle of least action. ... Huygens propounded an undulatory theory of light, while Newton, calling on an analogy with the material point dynamics that he created, developed a corpuscular theory, the so-called "emission theory", which enabled him even to explain, albeit with a contrived hypothesis, effects nowadays considered wave effects, (i.e., Newton's rings).

In the opinion of Léon Rosenfeld, a close colleague of Niels Bohr, "... Schrödinger [was] inspired by Hamilton's beautiful comparison of classical mechanics and geometrical optics ..."[19]

The first textbook in English on wave mechanics[20] devotes the second of its two chapters to "Wave mechanics in relation to ordinary mechanics". It opines "... de Broglie and Schrödinger have turned this false analogy into a true one by using the natural Unit or Measure of Action, h, .... ... We must now go into Hamilton's theory in more detail, for when once its true meaning is grasped the step to wave mechanics is but a short one—indeed now, after the event, almost seems to suggest itself."[21]

According to one textbook, "The first part of our problem, namely, the establishment of a system of first-order equations satisfying the spacetime symmetry condition, can be solved in a very simple way, with the help of the analogy between mechanics and optics, which was the starting point for the development of wave mechanics and which can still be used—with reservations—as a source of inspiration."[22]

Recently the concept has been extended to wavelength dependent regime.[23]

References

[edit]
  1. ^ Hamilton, W.R., (1834).
  2. ^ Kemble, E.C. (1937), pp. 7–10.
  3. ^ a b Lanczos, C. (1949/1970). Lanczos wrote on p. 136: "[Maupertuis] ... thus pointed to that remarkable analogy between optical and mechanical phenomena which was observed much earlier by John Bernoulli and which was later fully developed in Hamilton's ingenious optico-mechanical theory. This analogy played a fundamental role in the development of modern wave-mechanics."
  4. ^ Synge, J.L. (1954). On p. 2, Synge writes: "... the analogy between Newtonian mechanics and geometrical optics is completed only when we supplement the former by thinking of waves in association with the paths of particles. This completion was actually present in Hamilton's theory, since he made it so wide as to include both corpuscular and wave theories of light, and in the former interpretation his surfaces of constant action are the waves in question. Thus, since the time of Hamilton we have actually had what might be called 'Newtonian geometrical mechanics', based on the principle of Maupertuis, δ ∫v ds = 0, where v is given in terms of energy by mv2/2 = E − V."
  5. ^ Messiah, A. (1961), pp. 53–55.
  6. ^ a b Arnold, V.I. (1974/1978), p. 252.
  7. ^ a b Born, Max; Wolf, Emil (1993). Principles of optics: electromagnetic theory of propagation, interference and diffraction of light (6. ed., reprinted (with corrections) ed.). Oxford: Pergamon Press. ISBN 978-0-08-026481-3.
  8. ^ Schrödinger, E. (1926/1928), p. ix.
  9. ^ Schrödinger, E. (1926/1928), p. 13
  10. ^ a b c d Houchmandzadeh, Bahram (May 2020). "The Hamilton–Jacobi equation: An alternative approach". American Journal of Physics. 88 (5): 353–359. arXiv:1910.09414. Bibcode:2020AmJPh..88..353H. doi:10.1119/10.0000781. ISSN 0002-9505. S2CID 204800598.
  11. ^ a b c Masoliver, Jaume; Ros, Ana (1 January 2010). "From classical to quantum mechanics through optics". European Journal of Physics. 31 (1): 171–192. arXiv:0909.3258. Bibcode:2010EJPh...31..171M. doi:10.1088/0143-0807/31/1/016. ISSN 0143-0807. S2CID 14765944.
  12. ^ Arnold, V.I. (1974/1978), p. 250.
  13. ^ Messiah, A. (1961), pp. 224–225.
  14. ^ Joas, Christian; Lehner, Christoph (2009). "The classical roots of wave mechanics: Schrödinger's transformations of the optical-mechanical analogy". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 40 (4). Elsevier BV: 338–351. Bibcode:2009SHPMP..40..338J. doi:10.1016/j.shpsb.2009.06.007. ISSN 1355-2198. S2CID 122826763.
  15. ^ Schrödinger, E. (1926) p. 1049.
  16. ^ Schrödinger, E. (1928), p. 1.
  17. ^ de Broglie, L. (1923).
  18. ^ de Broglie, L. (1924).
  19. ^ Rosenfeld, L. (1971/1979), on p. 286.
  20. ^ Jammer, M. (1966), p. 366.
  21. ^ Biggs, H.F. (1927), pp. 50, 52.
  22. ^ Frenkel, J. (1934), p. 260.
  23. ^ Khan, Sameen Ahmed (February 2017). "Hamilton's optical–mechanical analogy in the wavelength-dependent regime". Optik. 130: 714–722. doi:10.1016/j.ijleo.2016.10.112.

Bibliography of cited sources

[edit]
  • Arnold, V.I. (1974/1978). Mathematical Methods of Classical Mechanics, translated by K. Vogtmann, A. Weinstein, Springer, Berlin, ISBN 978-1-4757-1695-5.
  • Biggs, H.F. (1927). Wave Mechanics. An Introductory Sketch, Oxford University Press, London.
  • de Broglie, L. (1923). Waves and quanta, Nature 112: 540.
  • de Broglie, L., Recherches sur la théorie des quanta (Researches on the quantum theory), Thesis (Paris), 1924; de Broglie, L., Ann. Phys. (Paris) 3, 22 (1925). English translation by A.F. Kracklauer
  • Cohen, R.S, Stachel, J.J., editors, (1979). Selected papers of Léon Rosenfeld, D. Reidel Publishing Company, Dordrecht, ISBN 978-90-277-0652-2.
  • Jammer, M. (1966). The Conceptual Development of Quantum Mechanics, MGraw–Hill, New York.
  • Frenkel, J. (1934). Wave mechanics. Advanced General Theory, Oxford University Press, London.
  • Kemble, E.C. (1937). The Fundamental Principles of Quantum Mechanics, with Elementary Applications, McGraw–Hill, New York.
  • Hamilton, W.R., (1834). On the application to dynamics of a general mathematical method previously applied to optics, British Association Report, pp. 513–518, reprinted in The Mathematical Papers of Sir William Rowan Hamilton (1940), ed. A.W. Conway, A.J. McConnell, volume 2, Cambridge University Press, London.
  • Lanczos, C. (1949/1970). The Variational Principles of Mechanics, 4th edition, University of Toronto Press, Toronto, ISBN 0-8020-1743-6.
  • Messiah, A. (1961). Quantum Mechanics, volume 1, translated by G.M. Temmer from the French Mécanique Quantique, North-Holland, Amsterdam.
  • Rosenfeld, L. (1971). Men and ideas in the history of atomic theory, Arch. Hist. Exact Sci., 7: 69–90. Reprinted on pp. 266–296 of Cohen, R.S, Stachel, J.J. (1979).
  • Schrödinger, E. (1926). An undulatory theory of the mechanics of atoms and molecules, Phys. Rev., second series 28 (6): 1049–1070.
  • Schrödinger, E. (1926/1928). Collected papers on Wave Mechanics, translated by J.F. Shearer and W.M. Deans from the second German edition, Blackie & Son, London.
  • Schrödinger, E. (1928). Four Lectures on Wave Mechanics. Delivered at the Royal Institution, London, on 5th, 7th, 12th, and 14th March, 1928, Blackie & Son, London.
  • Synge, J.L. (1954). Geometrical Mechanics and de Broglie Waves, Cambridge University Press, Cambridge UK.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Hamilton%27s_optico-mechanical_analogy&oldid=1188214385"